基于GJR-EGARCH模型的人民币汇率非对称特征分析
孙 颖
(安徽工程大学 经济与管理学院,安徽 芜湖 241000)
0 引言
汇率是各国货币之间的兑换比率,是各国制定宏观经济政策、把握金融市场规律的重要参照变量.汇率波动影响国民经济运行、国际贸易、外商投资等领域的均衡性.2005年7月汇率制度改革后,我国人民币实行浮动汇率制度,不再盯住单一美元,市场化程度加深,呈现升稳交替的现象.当前,在全球经济一体化背景下,各国之间货币关系日益紧密,人民币汇率波动状况日益复杂多变.因此,迫切需要一种能科学客观分析汇率波动特征及效应的工具,准确识别和测算人民币汇率的波动特征及其规律,帮助投资者更好地把握汇率走势、设计投资策略、防范汇率风险,实现汇率市场及经济运行的稳定性,同时为我国货币政策制定和汇率制度改革提供一定的参考.
对于汇率问题的研究,国外学者采用了多种方法,如:Meyer等采用SV模型分析了英镑汇率的杠杆效应[1].Wilfling采用Markov状态转移法分析了欧洲货币联盟成员国汇率的波动特征[2].自2005年汇率制度改革后,人民币不再盯住单一美元.2010年人民币汇率形成机制又得到了进一步推进.这种情况下,传统正态分布假设已不适用于人民币汇率研究.国内学者在“哪种模型更为科学合理”这一问题上也存在很大争论.苏岩,杨振海指出ARMA模型不适用于刻画汇率的走势特征[3].刘潭秋[4]、靳晓婷等[5]指出人民币汇率具有显著的非线性门限效应.刘姝伶等采用人民币兑美元汇率分别建立ARIMA模型和GARCH模型,并对比得出GARCH模型预测效果更好[6].吴跃明找出了人民币汇率的长记忆性特征[7].翟爱梅运用GARCH模型刻画了人民币汇率兑美元汇率的波动规律[8].傅魁等采用MEEMD组合模型预测了欧元兑美元汇率[9].陈黎明等采用CEEMDAN组合模型预测了人民币汇率走势特征[10].蔡彤娟等[11]、周春应等[12]分析了人民币与“一带一路”沿线国家汇率的动态关系.
已有研究多集中于人民币与美元之间的比率,然而,随着“一带一路”倡议的稳步推进,我国与沿线国家建立了多个境外经贸合作区、国际经济合作走廊等,因此,人民币与欧元之间的比价研究值得关注.本文以欧元兑人民币汇率日值为测量指标,选取2010年1月1日至2020年10月9日间共2 811个数据,分析其波动特征及规律,为我国汇率制度改革提供决策参考.
1 研究方法
经典线性回归模型通常假定随机误差项具有同方差性.但金融资产序列的随机误差项不满足这个假设.条件异方差模型突破了经典线性回归模型的这一局限,能够很好地解释汇率日值数据的非线性依赖性.因此,GARCH族模型被广泛地应用于金融时间序列的研究中.
1.1 GARCH模型
如果回归方程的随机误差项存在ARCH效应,则可使用自回归条件异方差模型和GARCH模型来拟合随机误差项的条件方差.对于ARCH(q)模型,一般形式如式(1)和式(2)所示:
rt=μt+εt
(1)
(2)
其中,式(1)为均值方程,式(2)为条件方差方程.
对于GARCH(p, q)模型,误差项的条件方差一般形式如式(3)所示:
(3)
其中,p是自回归GARCH项的阶数,q是ARCH项的阶数,α0≥0,αi≥0,βi≥0.
1.2 GJR模型
GJR模型也称为TARCH模型,对于GJR(p, q)模型,有如下一般形式:
(4)
其中,It-1为虚拟变量.对于条件方差的非负数要求是α0≥0,αi≥0,β≥0,α1+γ≥0.
1.3 EGARCH模型
对于金融时间序列可能存在的“杠杆效应”,EGARCH模型能够描述冲击的非对称性,且无须加入系数非负约束.对于EGARCH(p, q)模型,其条件方差如式(5)所示:
(5)
其中,γi=0,则不存在非对称效应;γi≠0,则存在杠杆效应.
2 实证分析
2.1 数据来源
采集2010年1月1日至2020年10月9日的欧元兑换人民币汇率日值数据作为样本(共2 811个),数据全部来源于国家统计外汇管理局网站.将汇率的时间序列记为EFR,并将数据分为两个部分:2010年1月1日至2019年12月31日的数据用以建模,2020年1月1日至2020年10月9日的数据用以拟合检验.
2.2 数据特征
对EFR序列进行对数变化以减少估计误差,其自然对数序列记为LNEFR.构建随机游走模型以验证序列的特征(表1).
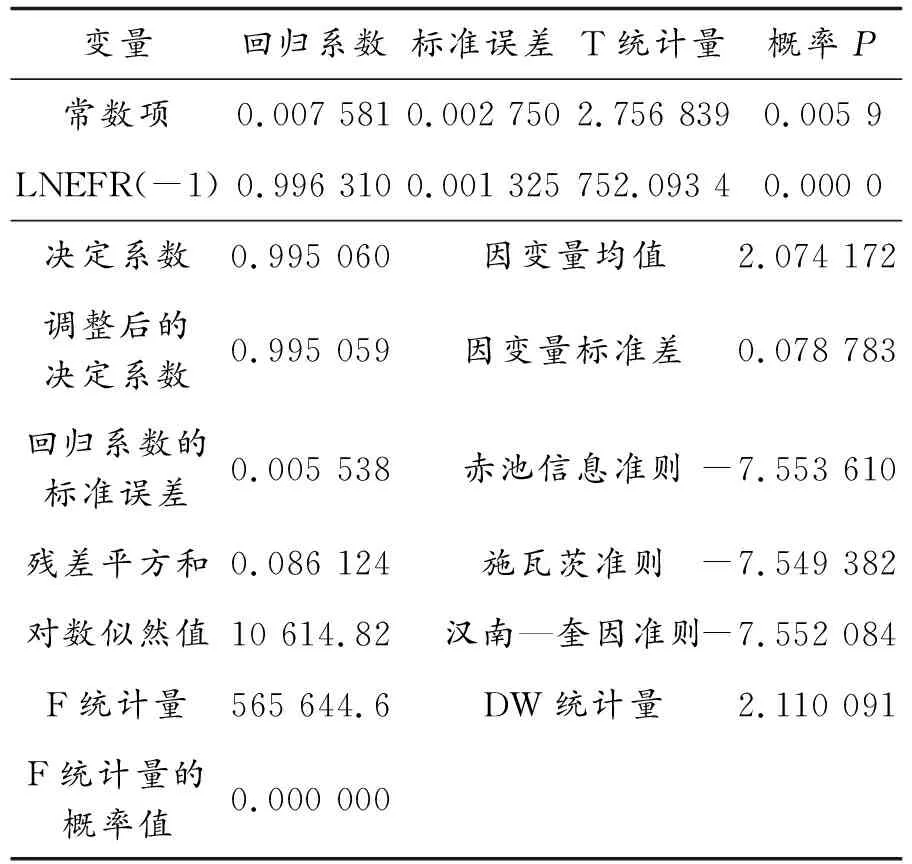
表1 随机游走模型的估计结果
(6)
t统计量=(2.756 839)(752.093 4)
对随机游走模型的残差进行ARCH检验.绘制残差序列resid01的折线图(图1).
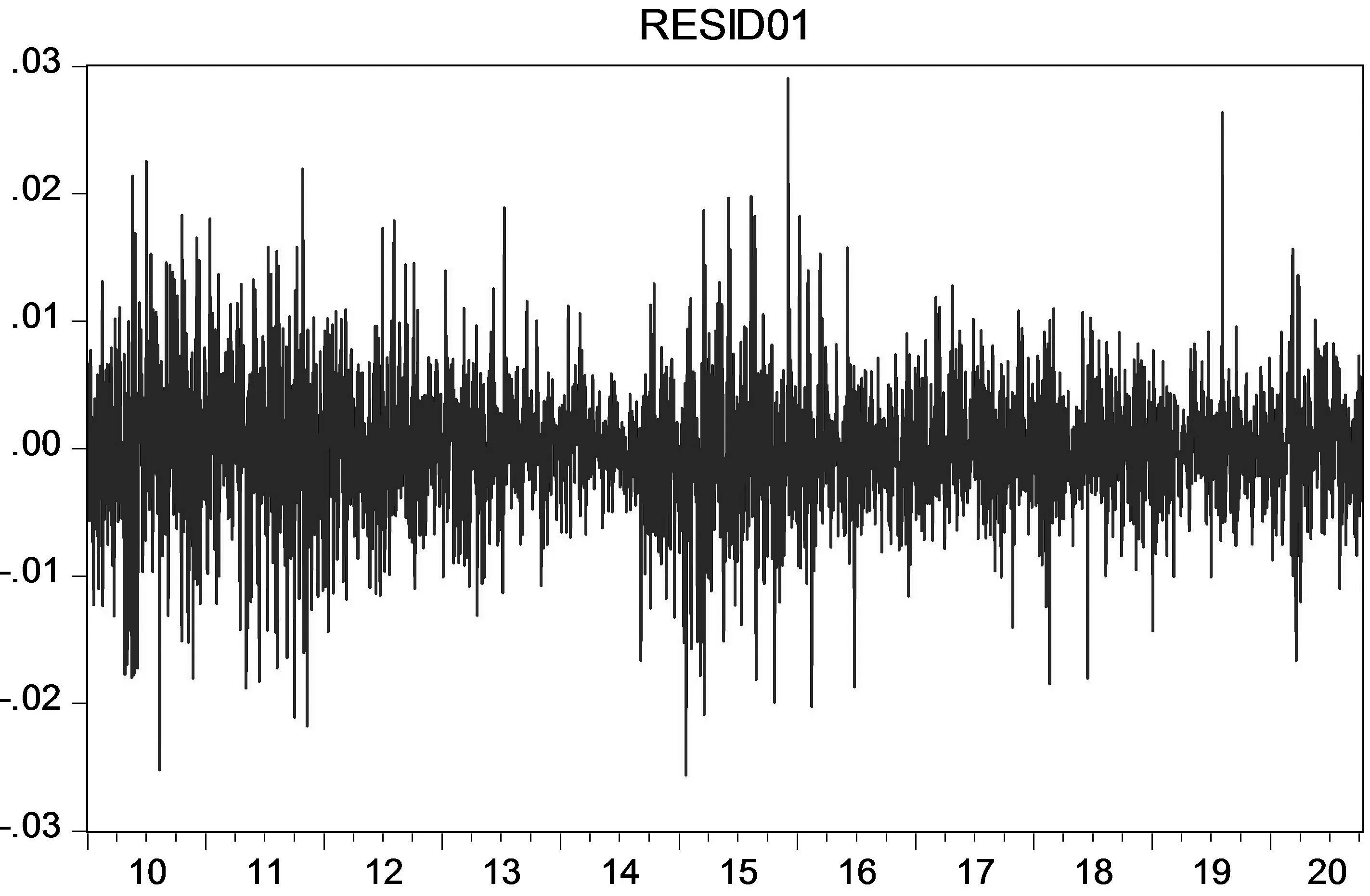
图1 残差序列resid01的折线图
残差序列有较强的“聚集性”,大的波动后面伴随着大的波动,小的波动后面伴随着小的波动,说明残差序列很可能存在条件异方差性.采用ARCH-LM检验法检验残差序列的ARCH效应(表2).

表2 残差序列的ARCH效应检验结果
F统计量=16.812 64,其概率值P远小于0.05,表明所有滞后残差平方项是联合显著的.ARCH效应的检验统计量是Obs*R-squared=159.193 1,概率值P也远小于0.05,因此拒绝“残差不存在ARCH效应”的原假设,即认为残差序列存在条件异方差性.
2.3 模型构建
(1)收益率序列特征分析
生成收益率序列,rt=ln(yt)-ln(yt-1),其中,yt为第t日欧元兑人民币汇率收盘价,yt-1为第t-1日欧元兑人民币汇率收盘价.为判断序列是否存在自相关性,绘制序列rt的自相关-偏自相关图(图2).
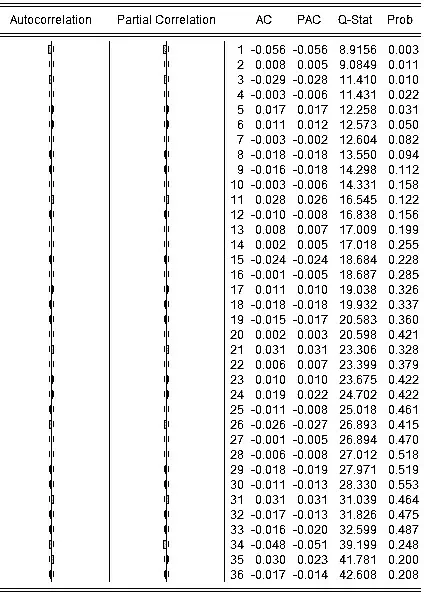
图2 收益率序列的自相关-偏自相关图
由图2可知,收益率序列r的自相关函数和偏自相关函数大多在95%的置信区域内,且Q统计量的概率值都大于10%的检验水平,可以判断收益率序列r不存在自相关性.进一步做人民币收益率序列的分布图,运用直方图和基本统计量信息对其特征进行初步分析(图3).
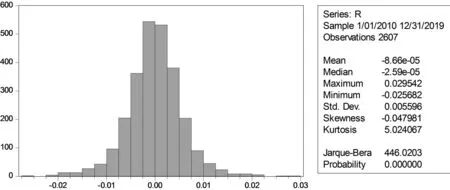
图3 人民币收益率分布图
由图3可知,人民币收益率序列r的概率分布是非对称的,偏度S=-0.047 981<0,表明序列r呈左偏分布,“左尾”拖得较长,这与人民币面临的升值压力有关.峰度K=5.024 067>3,表明序列r波动剧烈,且出现极端事件的可能性大于正态分布假设下的发生概率.与“S=0,K=3”的标准正态分布相比,序列r呈现明显的“尖峰厚尾”特征.同时,J-B统计量为446.020 3,P值为0.000 0,从而可以判定人民币收益率序列不服从正态分布.
由于序列r的均值μ=-0.000 086 6,非常接近于0,需要对序列r进行均值等于0的假设检验(表3).

表3 均值检验结果
t统计量=-0.790 424,其相应的概率值P=0.429 4,因此不能拒绝“均值等于0”的原假设,从而表明收益率序列r的平均收益率为0.综上,收益率序列r的分布具有尖峰厚尾、非对称、波动聚集性以及零均值等特征.
(2)非对称性效应分析
采用GJR模型对收益率序列r建立非对称的ARCH模型.由于收益率序列具有“厚尾”特征,因此,对于随机误差项的分布假设,采用比正态分布假设的尾部更厚的Student’s t分布,模型估计结果如表4所示.
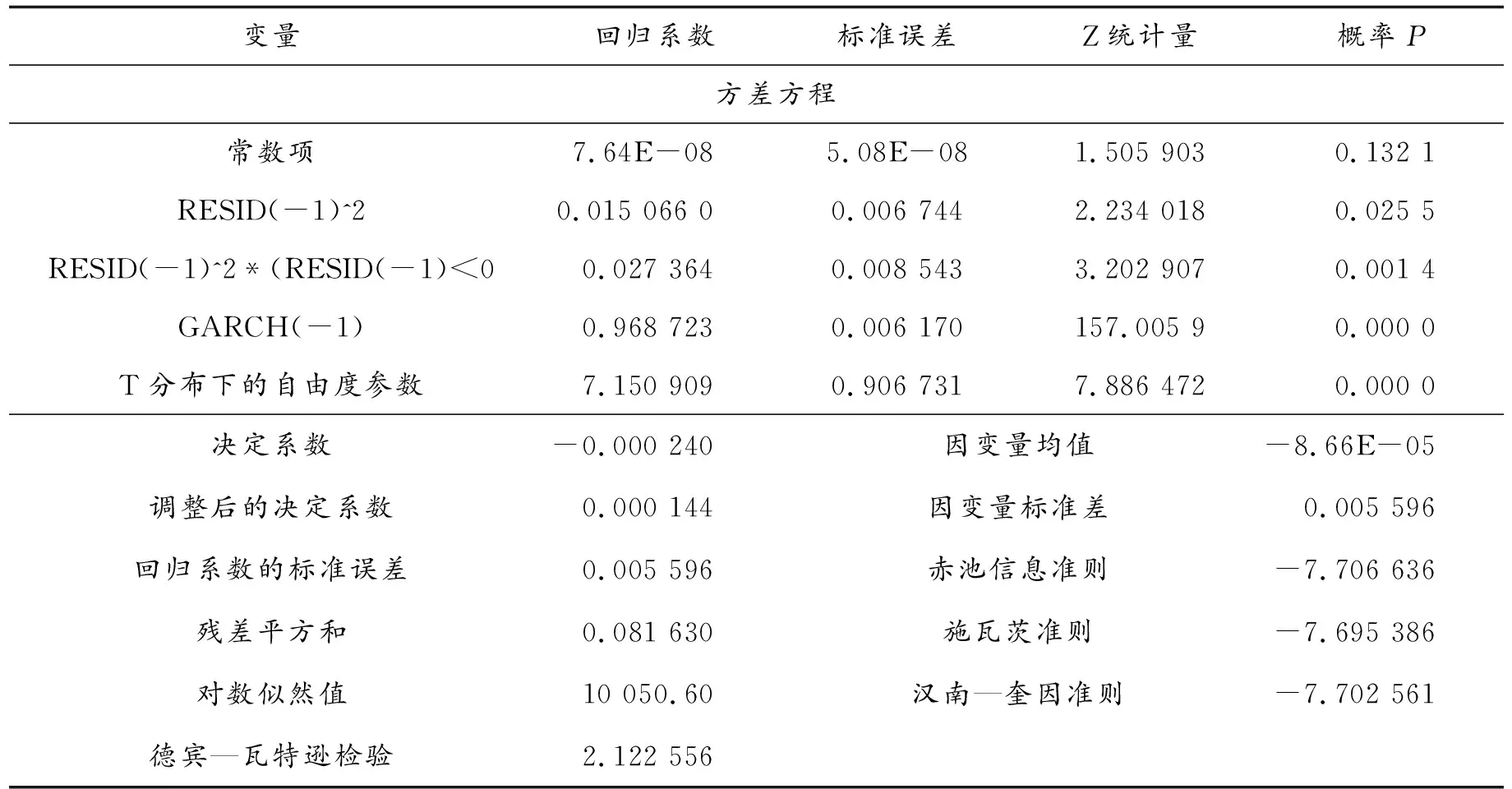
表4 收益率序列r的GJR模型估计结果
模型估计结果的系数估计值均为正,满足模型对参数非负约束要求,非对称项的系数估计值为正数且z统计量显著,说明序列存在非对称效应.由于结果中的自由度估计值为7.150 909,且z统计量也是显著的,因此,分别设定自由度为7和8,重新进行估计.根据AIC准则和SC准则判定,自由度为7的模型更优.由于ARCH项不显著,将ARCH项去掉,重新估计结果如表5所示.
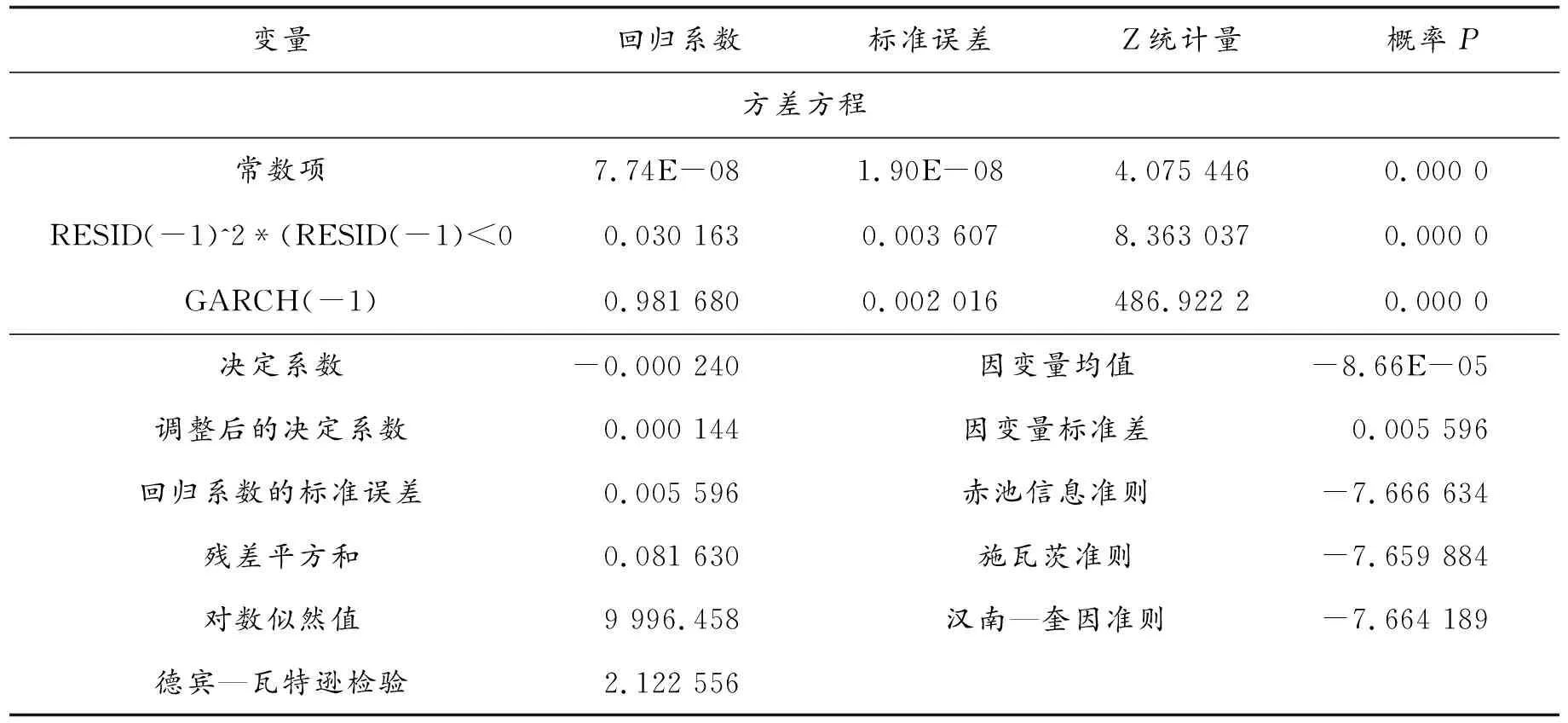
表5 GJR(1,0)模型估计结果
GJR(1,0)模型的参数估计值变化不大,但模型更简洁.GJR(1,0)模型条件方差方程如式(7)所示:
(7)
z统计量=(4.075 446)(8.363 037)(486.922 2)
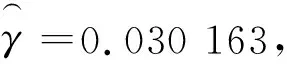
(3)杠杆效应分析
由于EGARCH模型可以用于描述市场信息冲击对波动的影响程度,且无须施加对参数符合的任何限制,因此,采用EGARCH模型进一步分析汇率波动的“杠杆效应”,估计结果如表6所示.

表6 EGARCH模型估计结果
其中,假定误差项μt服从学生t分布,自由度df估计值=7.310 876,其z统计量=7.666 578.由EGARCH(1,1)模型的估计结果得到条件方差方程,如式(8)所示:
(8)
Z统计量=(-3.425 809)(5.072 568)(-3.093 586)(525.154 0)
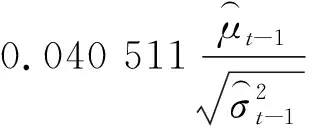
为进一步观察正的冲击和负的冲击对汇率波动的非对称影响效果,把握标准化残差变动一个单位引起的条件方差的变动情况,绘制EGARCH模型的信息冲击曲线(图4).
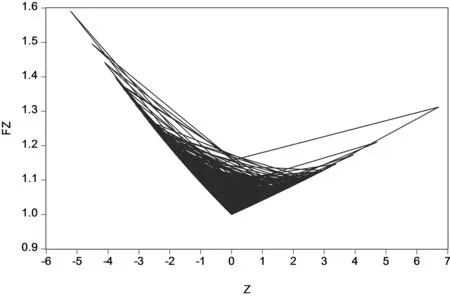
图4 信息冲击曲线
在0值左边,信息影响曲线斜率的绝对值较大,走势较陡峭;在0值右边,信息影响曲线斜率的绝对值相对较小,走势相对较为平缓,说明负的冲击比正的冲击对波动性的影响更大,非对称性明显.
(4)EGARCH模型拟合检验
采用2020年1月1日至2020年10月9日的数据拟合检验EGARCH模型对汇率波动率的动态预测效果,结果如图5所示.
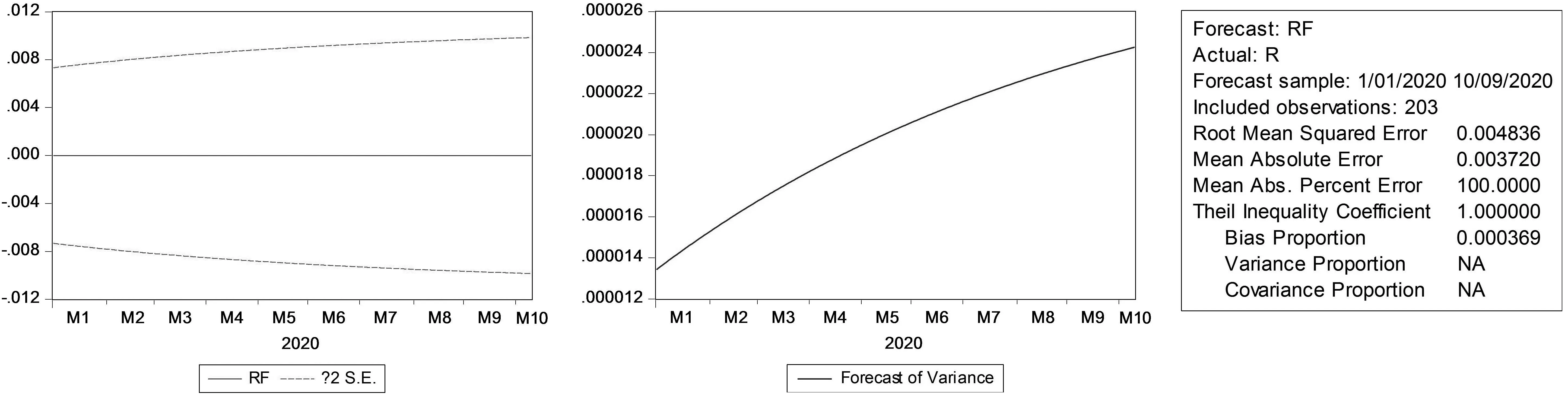
图5 预测结果拟合检验图
由图5可知:收益率序列的预测值RF为一条过零值直线.收益率序列预测值95%的置信区间范围波动幅度很小,随着预测期的增加而小幅变宽. 条件方差预测值缓慢增加,最后收敛于0.000 024附近,说明模型预测是精准的.
3 结论
本文采用GJR-EGARCH模型分析了人民币汇率的波动特征及其规律,模型能对样本区间内的汇率进行拟合、特征分析等,在此基础上得到以下主要研究结论:
(1)人民币汇率具有明显的随机游走特征
由随机游走模型估计结果得到人民币汇率序列是一个不带漂移项的随机游走过程.
(2)人民币汇率存在明显的集聚性.
由残差检验得到人民币汇率存在明显的波动集聚性,即存在ARCH效应.
(3)人民币汇率具有一般金融数据的特征.
在样本区间内,人民币汇率具有“尖峰厚尾、左偏、非正态分布”的分布特征.
(4)人民币汇率具有杠杆效应.

