集中式自主定轨算法在星载计算机集群上的并行实现

冯凌璇，林宝军，，5，刘迎春，林 夏

（1.中国科学院空天信息创新研究院，北京 100094；2.中国科学院大学，北京 100049；3.中国科学院微小卫星创新研究院，上海 201210；4.上海微小卫星工程中心，上海 201210；5.上海科技大学，上海 201210）

随着北斗三号全球导航系统的建成开通，北斗为全球提供高质量的定位和授时功能。而导航卫星的自主定轨能力直接影响系统的服务性能[1]。传统的集中式定轨算法复杂度高，不适用于实时的应用场景[2-3]。尽管分布式算法实时性好，但精度很难提高并且存在滤波发散的问题[4]。如何将集中式定轨算法应用到卫星上，国内有许多讨论[5-8]。但这些方法要么在精度上有所损失，要么受到星载计算机计算能力的限制。

由于单台星载计算机性能有限[9]，利用集群并行化的方法是实现星上复杂软件的一种可行方案。自主定轨算法这类科学应用通常具有较优的静态划分算法[10]。因此，该文提出一种集中式自主定轨算法的并行方案，在保证精度的同时有效减少单台星载计算机的运算资源的消耗。

1 集中式自主定轨算法并行优化方案

1.1 并行系统架构

中科院北斗三号卫星载有多台星载计算机，分工处理星上各类应用，星载计算机之间采用1553B总线通信。星载计算机集群的架构如图1 所示，属于总线式集群，多个计算节点通过1553B 总线相连。

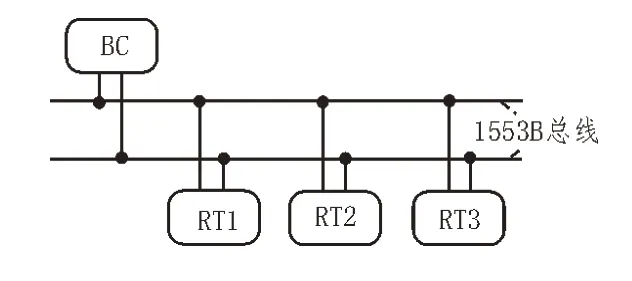
图1 系统架构

1553B 是一种在航空航天领域应用广泛的中央集权式总线协议[11]，总线的设计传输速率为1 Mb/s，总线上设备分为总线控制器（BC）、远程终端（RT）以及总线监视器（BM）。星载计算机集群上的计算节点作为RT 挂载在总线上。

1.2 并行编程模型

并行编程模型是一组程序的抽象，它将应用程序的并行行为配适到底层并行硬件[12]。在高性能计算机集群时代，MPI 一直是高性能计算领域中的一种标准实现方案[13]，但MPI 是为大规模具有高性能计算机的集群而设计的[14]，这些计算机通常拥有比星载计算机更加强大的处理器、更大的内存空间以及更加灵活的网络连接方式。因此，直接将MPI 迁移到现有的星载计算机集群上将会面临巨大的挑战。

针对现有1553B 连接的总线式星载计算机集群，该文基于MPI 原理设计了一种可以用于星上计算机集群的总线式消息传递式的并行编程模型——sMPI，可以实现多台星载计算机之间的协同处理计算。该并行编程模型在星载计算机上实现了MPI 模型的大部分库函数功能，向上层应用提供通用的标准MPI 编程接口，支持C 语言的开发，便于开发者直接将地面程序移植到星载计算机上。

在1553B 总线协议中，总线采用命令响应方式实现系统通信[15]。命令字只能由BC 发出，而作为并行任务进程执行者的RT 没有发送数据的主动权。这样的总线结构极大限制了任务进程的灵活性。sMPI 通过合理设计数据帧格式实现了在BC 控制下的计算节点RT 之间的通信。BC 通过对总线上所有的RT 进行轮询实现消息的转发。但是，若轮询的周期过长，数据的发送则不能充分利用总线带宽，总线吞吐率低；若轮询周期过短，那么频繁的总线中断会影响单个节点的性能。考虑到并行程序的数据交互具有很高的时间局部性，一旦发生数据交互，则很大可能伴随着大量的数据交互。sMPI 通过式（1）来控制BC 的轮询周期时间。当有数据交互时就快速提高轮询频率，数据交互结束则缓慢降低轮询频率，在提高数据交互吞吐率的同时又避免了频繁的中断。

在实现过程中，轮询周期时长的最小单位为1553B 总线的周期T1553，即Tmin，Tmax可取100 个总线周期时间。初始时，T0取Tmax。若上一轮询周期不存在数据交换，下一轮询周期Tn+1则在原Tn的基础上加5T1553；若存在数据交换，Tn+1则取Tn的一半并取整。

1.3 并行算法描述

并行化前的串行集中式自主定轨使用推广卡尔曼滤波算法，算法流程如图2 所示，算法初始化后首先接收星间链路测距值，然后对整网卫星根据动力学模型进行轨道钟差信息的预报，接着根据采集的测距值导出观测值信息，最后完成当前周期整网卫星轨道钟差信息的滤波更新。待整网卫星轨道钟差信息更新完毕后，算法生成各子卫星星历，下发于各子卫星中。星上每隔一段时间执行一次自主定轨算法，从而实现卫星长时间的高精度自主定轨。

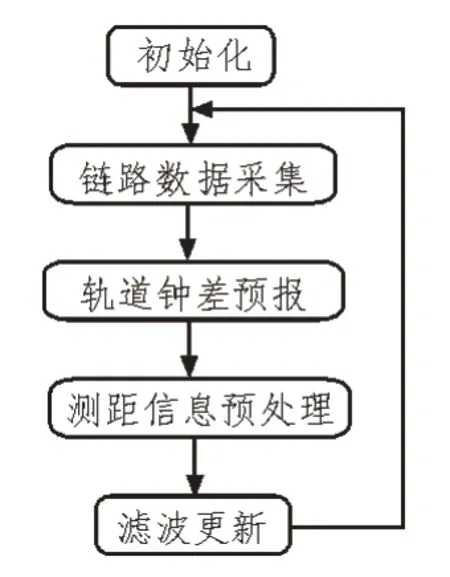
图2 串行集中式自主定轨算法

在集中式自主定轨算法中，运算主要集中在轨道钟差预报以及滤波更新这两个模块中。在串行算法中，轨道钟差模块每个周期算法需要对每一颗卫星完成钟差和轨道的预报，其过程由式（2）～（4）给出：

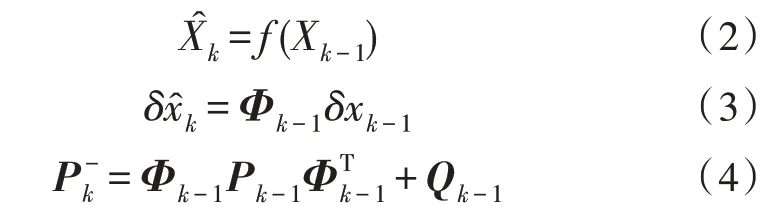
其中，Φ为转移矩阵，P为协方差矩阵，Q为噪声矩阵。因此，对于每颗卫星而言，该部分的计算是一致且互不干扰的，易于并行化处理。而在滤波模块，滤波过程由式（5）～（8）给出：

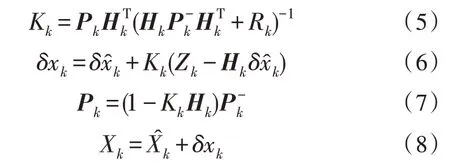
其中，H为观测矩阵，Z为观测量。在滤波模块中，P为全局变量，包含了所有卫星之间的协方差，但通过合理的划分以及补偿算法可以将这一全局矩阵划分成若干子矩阵分散到不同节点中，在保证算法精度的同时极大提升算法效率。

考虑到这些算法的特征，集中式自主定轨的并行算法采用多进程的方式将整网的卫星和链路数据分散到集群的多个计算节点上同时进行解算。

图3为并行集中式自主定轨的算法流程。并行算法通过数据分发、同步、收集来完成多进程的协同处理。在初始化时，主进程负责将整网卫星数据划分为若干子集并将卫星初始化信息分发到各个进程中；在每个算法周期内，主进程在完成链路测距值的采集后对链路数据进行分发，链路根据两端点卫星是否均包含在同一卫星子集中可分为域内链路和域间链路；各进程完成卫星轨道钟差预报后相互交换数据，进行同步。

在智慧图书馆背景下，图书馆服务不仅要从馆内向馆外拓展，而且要从被动等待向主动寻求转变。图书馆服务的优劣，有赖于图书馆员是否有敏锐的洞察力和非凡的创造力，是否能够时刻关注用户需求，了解如何利用新技术、建设新资源，最大程度地满足用户需求，提升服务质量。这要求图书馆员不仅要有扎实的专业能力，而且要有执着的服务信念。

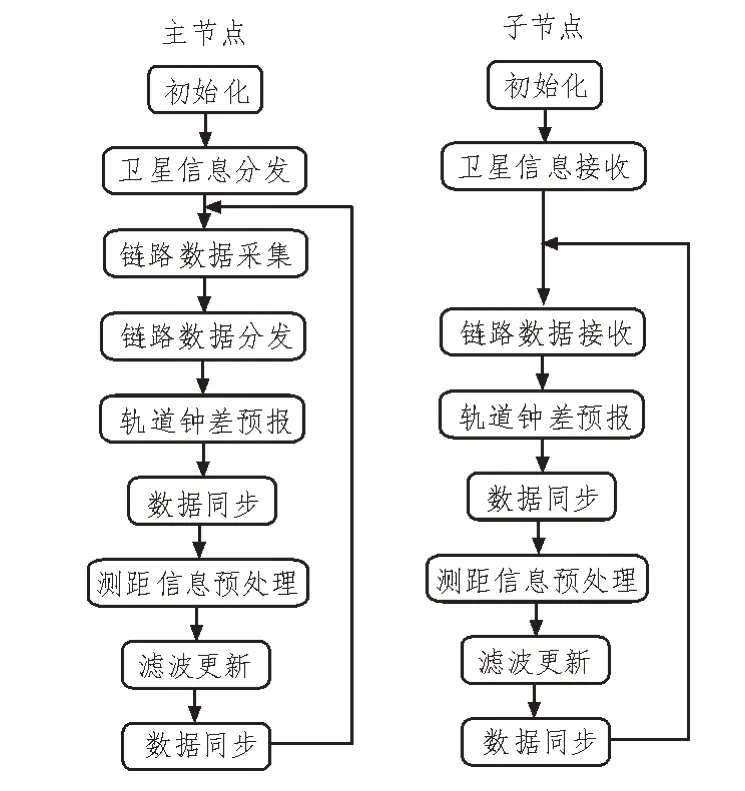
图3 并行集中式自主定轨算法

在最后的滤波更新模块中，各进程分别利用星间测量值与预报信息进行卡尔曼滤波。在串行集中式自主定轨算法中，滤波过程（式（5）～（8））需要维护大小为(D×n)2的协方差矩阵P以及大小为NL×D×n的测量矩阵H，其中，D是状态量的维数，NL是生成导出双向测距值的数目。于是滤波过程涉及的高维矩阵乘法算法复杂度可达到O(n3×NL)。并行算法中，对原协方差矩阵取广义对角，即每个进程只需要维护(D×nm)2大小的协方差矩阵，其中nm为子进程负责维护的卫星数目。由于只保留协方差的广义对角矩阵而舍弃了其他元素，因此相对串行算法，该并行方案会损失一定的精度。但另一方面，这样可以极大地提高算法解算速度，并且损失的精度在一定限度内是为工程所允许的。相对地，测量矩阵的计算与串行算法也有一些区别。在串行算法中，链路有测量矩阵以及噪声，如式（9）：

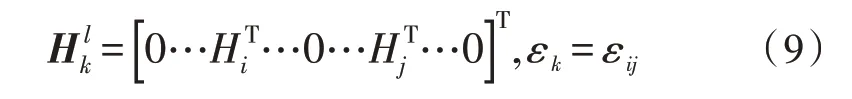
由于并行算法对整网卫星进行了划分，存在域内链路和域间链路，域内链路的两端点卫星都在同一进程所计算的卫星子集内，测量矩阵及噪声与串行算法一致；域间链路的两端点卫星中有一个端点卫星不在卫星子集内，于是只需要更新子集内的卫星信息。测量矩阵及噪声表示为：

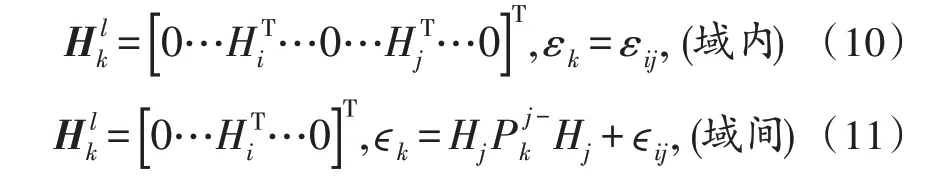
2 地面集群仿真结果

地面仿真利用亚马逊的EC2 构建一个小型地面集群对并行方案进行可行性分析以及规律探讨。在所构建的集群中，每一台实例拥有一个有效核，每个核的有效进程数为1，运行内存为1 740 MB，最多有两个网络接口。地面仿真采用多进程的方式，不同进程运行在集群的不同实例上，进程之间采用消息传递的方式进行通信[16-19]。

仿真数据集一共包含24 颗MEO 轨道卫星，一个地面锚固站以及它们之间的240 条测距值，算法周期为300 s，测距精度为0.1 m。定轨精度通常由用户测距误差URE（User Range Error）来表示。表1 给出了不同计算节点数下30 天内平均URE 误差以及平均每周期运算时间的仿真结果。其中，p为计算节点数，即并行度。当p=1 时，为集中式定轨算法，p=24时，为传统的分布式定轨算法。

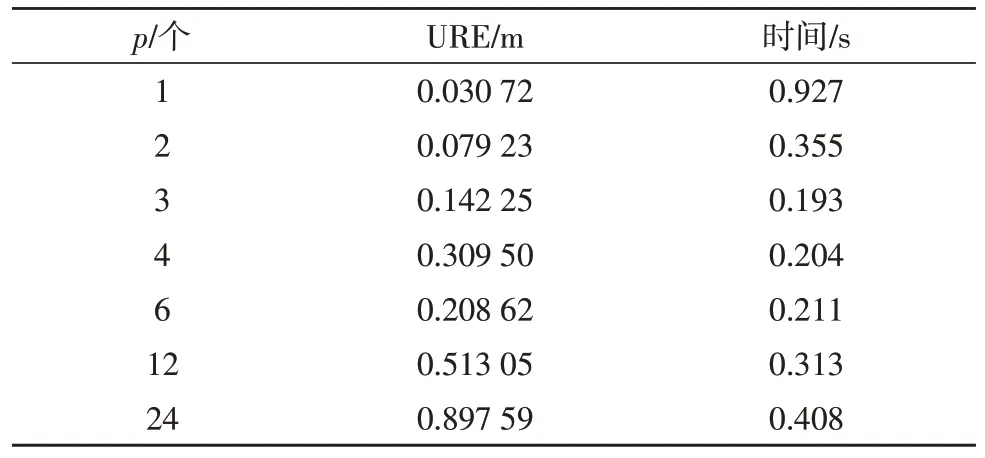
表1 计算节点数p和平均URE误差以及平均每个周期运算时间的关系

分析并行度（计算节点数）p对算法精度的影响。从表1 中可以发现尽管并行算法的计算精度相对于原始的串行算法有一定损失，但若并行度控制在一定限度内时，并行算法的URE 误差远低于分布式定轨算法。例如，当计算节点数为3 时，30 天的平均URE 误差仅为0.142 25 m，远低于分布式算法约0.9 m 的平均URE 误差。而计算性能方面，并行算法的计算性能却远高于原始的串行算法。计算节点数和加速比及平均URE 误差关系如图4 所示。

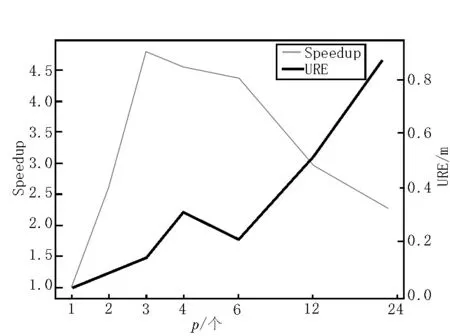
图4 计算节点数和加速比及平均URE误差关系

从图4 可以看出，当并行度不大于3 时，计算性能的提升明显，当p大于3 时，由于通信成本增加等因素，加速比反而逐渐降低。由于算法中不可并行部分以及通信成本的存在，一味地增加计算节点数并不能获得更高的计算加速比。在达到一定阈值时，增加节点数不能获得更好的计算性能。

地面集群的仿真结果验证了集中式定轨算法的并行优化方案是可行的，并且给出了不同并行度下算法精度和计算性能的规律，为并行算法在星载计算机集群上的实际应用提供预估和参考。

3 星载计算机集群仿真结果

基于1.1 节中描述的星载计算机集群架构构建仿真系统。该集群是一个同构计算机集群，集群中最多可以有3 个节点提供计算力，每一个计算节点均由龙芯1E+龙芯1F 处理器组成。龙芯1E 和1F 均为中科龙芯公司设计的宇航级抗辐照芯片[16]：1E 处理器作为节点的中央处理器，是一台单核处理器，采用双发射五级流水，主频为33 MHz，运行内存为128 MB，负责节点上应用程序的处理；龙芯1F 是龙芯1E 处理器的配套IO 桥芯片，在节点中主要负责外围的通信。并行算法应用到星载计算机集群的映射通过sMPI并行编程模型实现，集群中每个计算节点上运行一个进程，进程之间采用消息传递的方式共享数据。

星载计算机集群仿真所采用的测试数据集与地面仿真数据集相同，表2 给出了不同数目的卫星和链路下，并行算法平均每周期运算时间以及运行内存的占用情况。从表2 可知，与串行算法相比，并行算法有效地降低了单台星载计算机的运行负载压力，包括CPU 资源消耗以及运行内存消耗。当卫星数为24 颗时，算法加速比可以达到1.94，单台计算机节约了50%的运行内存。并且，随着卫星数目的增加，通信消耗的占比逐渐减少，加速比得到明显提升，当卫星总数达到48 颗，链路数达到928 条时，加速比达到了2.82，单台计算机的运行内存减少了55%。当卫星总数达到72 颗时，尽管运算时间从2 383 s降低到742 s，加速比达到3.20，但依旧超出了运算周期300 s 的限制。因此，对于更多的卫星和链路，3 台星载计算机的计算能力仍是有限的。另一方面，若采用更多的计算节点参与运算，星上通信开销将会成为另一瓶颈，因此，该并行方案对于中等规模的卫星和链路数据较为实用。若想扩展应用到更大规模的数据，参考地面集群的仿真结果则需要更多计算节点的参与，同时需要高速通信协议的配合。

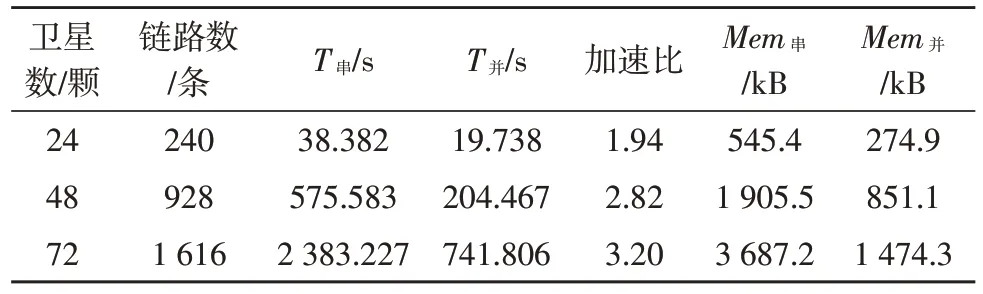
表2 串行算法和并行算法效率对比

4 结束语

该文针对传统串行集中式自主定轨算法提出了一种并行算法，并利用所设计的轻量级并行编程模型sMPI 在总线式星载计算机集群上实现了整网24颗MEO 卫星自主定轨。以24 颗卫星为例，当星载计算机集群中有3 个节点参与计算时，30 天平均URE误差为0.142 25 m，仅为分布式算法URE 误差的15.8%。在保证定轨精度的同时，并行优化算法显著降低了星载计算机的负荷。在以龙芯1E 为主处理器的集群上的仿真结果显示，当卫星数为24 时，3 个节点的加速比达到了1.94，平均19.738 s 就能生成整网轨道和钟差结果，单台星载计算机可减少约50%的内存占用。

面对中等规模的卫星数据，并行的集中式自主定轨算法在星载计算机集群上的表现良好，但面对卫星数量更多以及更加复杂的卫星网络，该文星载计算机集群架构依旧不能满足计算力需求。限制星载计算机集群性能的一方面是集群中计算节点的数目以及单台性能，另一方面是节点之间的通信开销。根据地面仿真数据结果，通过增加计算节点数的办法可以进一步提升计算性能，但由于算法中不可并行部分以及通信成本的存在，在节点数达到一定阈值之后，增加节点数不再能获得更高的计算加速比。因此，对于更多卫星和链路的大规模星座，在现有数目的星载计算机节点不能满足定轨计算需求的情况下，可以通过适当增加集群中计算节点数目的方式来解决，甚至可以考虑利用多颗卫星上的若干台计算机进行并行解算，或者采用高速通信协议来降低集群的通信成本开销。