基于客流多式出行选择的城轨列车运行计划与票价组合优化

李恒鑫

（中铁第四勘察设计院集团有限公司 线路站场设计研究院，湖北 武汉 430063)

0 引言

城轨列车运行计划决定了各线路在各运营时段内开行列车交路及其开行频率等，是城轨企业组织列车运行的基础。同时，城轨列车运行计划不仅决定列车运行成本，还直接影响着旅客出行服务水平，其与列车票价的结合很大程度上影响着旅客出行选择，从而也决定选择城轨出行客流量。

目前关于城市轨道交通列车运行计划与票价制定等方面已开展许多相关研究。Jamili等[1]研究城市轨道交通跨站停运营模式下列车运行计划的鲁棒优化。陈维亚等[2]提出了城市轨道交通快慢车与多站限流协同优化方法，Canca等[3]提出基于多交路运营模式的列车运行计划优化方法。Gkritza等[4]考虑多种交通方式的博弈构建不同的公共交通定价方法。邓连波等[5]基于弹性需求、票价率偏差最小化等构建城轨线路票价优化方法。刘清琰[6]实现了城轨网络快慢车开行优化方法。Larrain、王琳等[7-8]以乘客总出行时间最短和轨道交通运营企业运营成本最低为目标，建立非站站停列车开行方案的多目标优化方法。Vuchic[9]根据区域停、跨站停等快慢车停站特征，分析快慢车组合运行的适用性及运营效果。Mignone等[10]提出设计运营周期内各时段快慢车运行计划的优化模型。Lee等[11]将乘客根据出行起终点、换乘选择等分类，进而构建快慢车停站方案的优化方法。孙元广等[12]分别研究了城轨快慢车与Y型交路列车开行方案优化问题。周晓昭等[13]构建了考虑停运策略的城际列车运行计划调整双层规划优化方法。

虽然目前关于城轨列车运行计划与票价优化方面的研究较多，但是这些研究普遍将城轨系统作为一个封闭系统进行研究，即假定各OD出行需求不受城市内其他交通出行方式出行服务水平的影响，会一直采用城轨列车出行。显然，这种假设与实际存在一定差距，实际上OD出行需求交通方式选择会受到各种交通方式服务水平变化而发生改变，故需考虑城市常规公交线路及其服务水平对整个城市居民出行方式选择与出行路线选择的影响，优化轨道交通网络列车运行计划与票价。为此，结合客流多方式出行选择研究城轨列车运行计划与票价组合优化问题，在分析各交通方式出行费用的基础上，构建两者优化的双层规划模型，并设计模拟退火-遗传算法进行求解。

1 各交通方式出行费用分析

通常拥有私家车客流可选私家车、常规公交和轨道交通出行，而非拥有私家车客流仅选常规公交、轨道交通出行。记c，b，r分别代表私家车、常规公交和轨道交通出行方式，3种出行方式费用构成如下。

（1）私家车出行费用。选择私家车出行时不仅需要承担产生的各类时间费用，还需承担燃油费、折旧费、以及在起点与终点可能存在的停车费等，但无在出发点的步行与等待产生的费用。记为从出发点r驾车以路径p到达目的点s的成本，其计算公式为

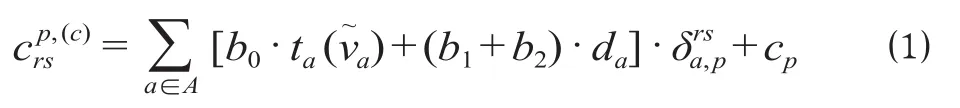
式中：tα()为路段α的行驶时间，min，其采用美国道路局函数(Bureau of Public Roads，BPR)公式计算；b0为拥有私家车客流出行时间价值，min；b1，b2分别为私家车单位里程燃油费与折旧费，元；dα为路段α里程，km；为路段-路径0-1关联变量，若路段α在路径p上，则= 1，否则为0；cp为使用路径p私家车出行的平均停车费用，元。

（2）常规公交出行费用。常规公交出行费用包括步行时间、站点等待时间、在车时间、换乘费用以及票价。定义，分别为拥有与非拥有私家车客流从出发点r以常规公交路径p到达目的点s的总出行费用，计算公式为

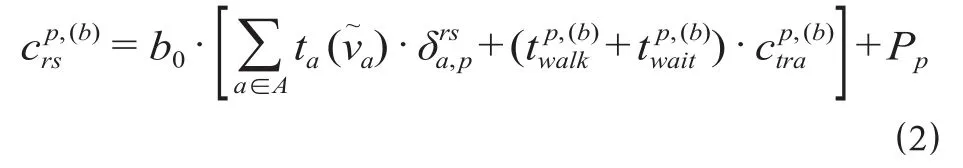
式中：，分别为公交路径p上的乘客步行总时间与公交站点平均等车时间，min；为公交路径p上的乘客换乘总时间，min；Pp为公交路径p上总票价，元。

计算公式为

式中：为非拥有私家车客流出行时间价值，元/min。

（3）轨道公交出行费用。轨道交通出行费用包括步行时间、站点等待时间、在车时间、舒适性惩罚以及票价。和分别表示拥有与非拥有私家车客流在区间e出行成本，其计算公式分别为

式中：we为区间e票价率，元/人公里，若e属于快车运行区间，则为快车票价率，否则为慢车票价率；te(de)为区间旅行时间，min；Fe(ve)为舒适性惩罚成本，元，其可视为轨道交通车辆内部拥挤造成的额外费用，随区间客流量增加而大幅增加，其计算公式为

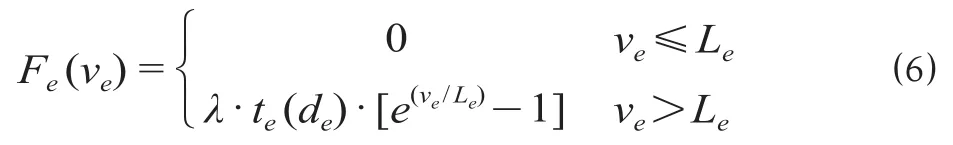
式中：λ为惩罚水平调整系数；Le与ve分别为列车区间e的最大载客能力与实际客流量，人。

类似地，定义，分别为拥有和非拥有私家车客流的从出发点r乘坐轨道交通以路径p到达目的点s的出行成本，其计算公式分别为

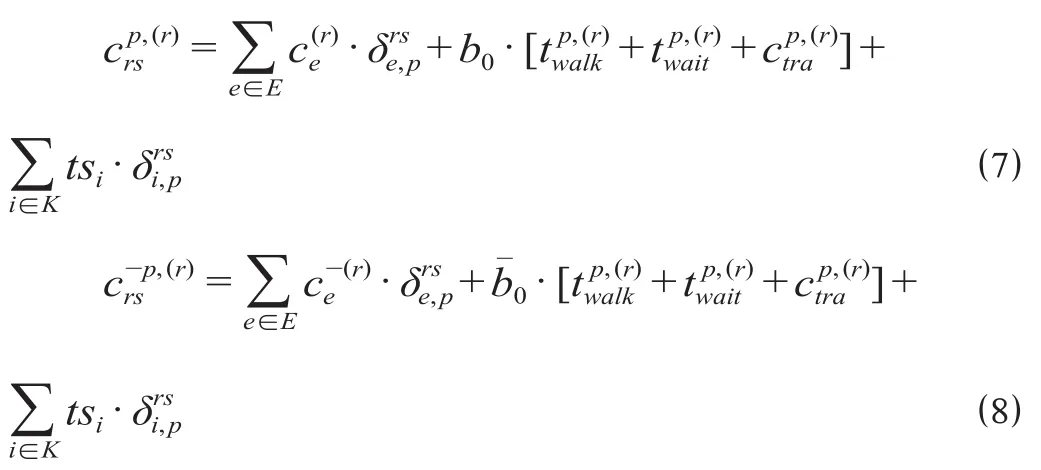
式中：，，为以城轨路径p出行需要的步行时间、等车时间以及在线路间换乘时间，min；为路段-路径0-1关联变量；为车站-路径0-1关联变量。

2 模型构建

考虑由城市轨道交通线网、道路路网、公交线网三者构成的城市综合出行网络，每条轨道交通线路均可组织开行快车、慢车2类列车，且慢车为必开行列车。城轨快慢车组合运行计划及其票价在很大程度上决定了城轨出行服务水平与服务能力，进而影响客流出行方式与出行路径的选择；反过来，客流出行方案选择又直接影响城轨列车运营效益等。以上决策过程可描述为一种“一主多从”主从博弈关系，基于该主从博弈关系，便可构建双层规划模型，其中将城轨列车运行计划与票价优化模型作为上层模型，将多类客流多方式混合交通均衡变分模型作为下层模型。

2.1 城轨列车运行计划与票价优化

模型在各城轨线路方向均开行长交路、站站停列车(以下简称“慢车”)的基础上，进一步优化确定研究运营时段内各城轨线路方向是否开行快车、开行快车停站以及开行快慢车数量；同时，在规定慢车票价率固定不变的基础上，优化确定各线路方向开行快车的票价率。记0-1决策变量xl表示城轨线路方向l是否开行快车，若开行，则xl= 1，否则xl= 0；记0-1决策变量yli表示城轨线路方向l开行快车在经由站i是否停车，若停车，则yli= 1，否则yli= 0；记非负整数决策变量αl，βl分别表示城轨线路方向l开行快、慢车数量；非负决策变量ωl表示城轨线路方向l开行快车的票价率。

模型选择以最大化城轨列车总票价收益为目标来优化城轨快慢车组合运行计划与票价方案，其目标函数为

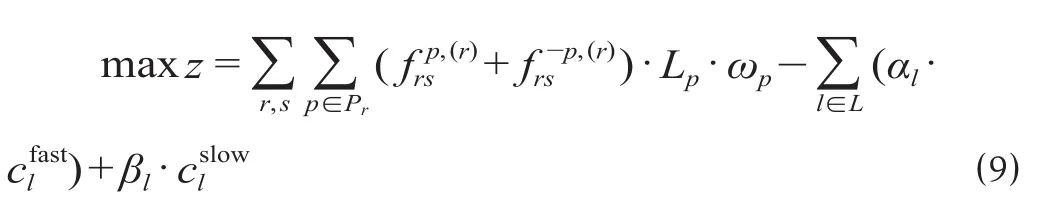
式中：，分别表示OD对(r，s)间轨道路径p上拥有私家车客流和非拥有私家车客流的出行量，其取值需通过求解以下下层模型获得。Lp为路径p里程，km；ωp为路径p票价率，元/人公里；，分别表示在城轨线路l上组织开行1列快车与慢车的成本，元。

模型相关决策变量必须同时满足以下5组约束条件。

（1）快车开行数量约束，即线路方向l在不组织开行快车时，其开行快车数量必为0；否则，开行快车数量不高于线路在研究运营时段最大通行能力Cαpl，该约束表示为

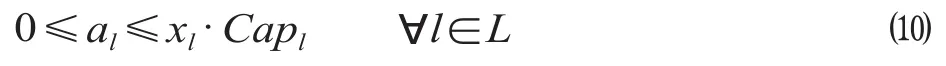
（2）快车停站设置约束，即线路方向l在组织开行快车时，也就是xl= 1时，停站数量应不小于2，但少于线路车站数nl；否则该线路方向快车不在任何车站停车，该约束表示为

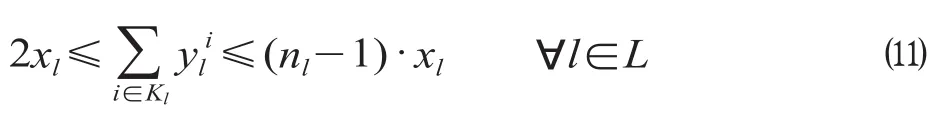
（3）快车票价率约束，即线路方向l若开行快车，其票价率应不低于慢车的票价率，同时也不能高于政府设置的最高指导价，该约束表示为

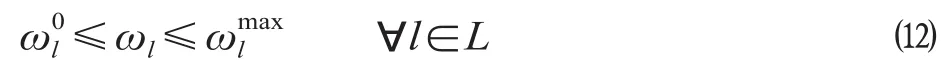
式中：与分别为线路l开行慢车的票价率及其上限值，元/人公里。

（4）区间通过能力约束，即在研究运营时段内，线路任意区间方向运行列车数不得高于该区间最大通行能力，该约束表示为

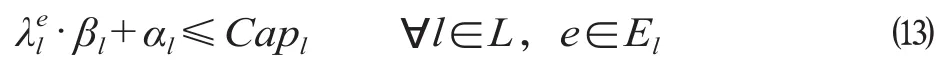
式中：为线路方向l所开行快车是否经由区间e。

（5）车站发车服务频率约束，即在研究运营时段内，线路任意区间方向运行列车数不得高于该区间最大通行能力；另一方面，也不得低于保证最低服务频率所需要运行的列车数，记ζmin为保证最低车站服务频率所需最小列车数，该约束表示为

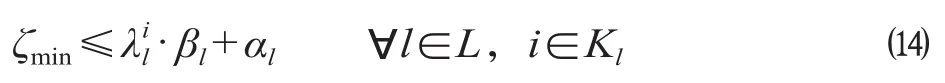
2.2 多类客流多方式混合交通均衡变分模型

基于上层模型所确定的城轨列车运行计划与票价，结合城市道路与公交网络便可构建乘客综合出行网络，在该网络上实现客流的多方式出行选择均衡分配，来评估当前城轨列车运行计划与票价方案实施的收益，即上层目标值。假设客流按Logit分离模型选择各交通方式与路径出行，则可将拥有与非拥有私家车2类客流在综合出行网络上的出行选择描述为一个多类客流多方式混合交通均衡分配问题，其等价于以下变分不等式。

模型以最小化各类出行旅客总出行费用为优化目标，即

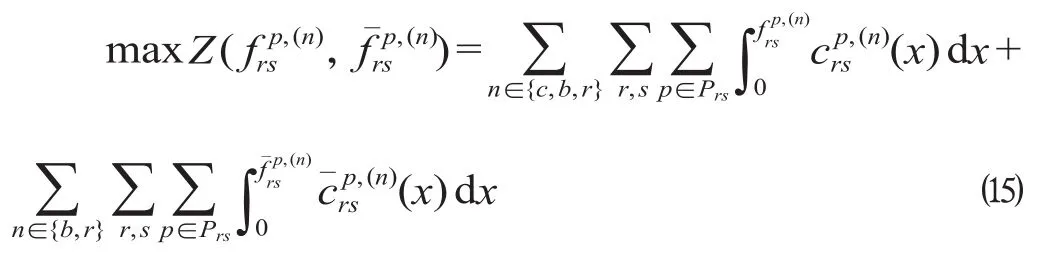
模型还需考虑以下3类约束。

（1）需求守恒约束，即对于任意OD，拥有与非拥有私家车客流选择各种交通出行方式的客流量总和应分别等于该OD相应的出行需求量，该约束可分别表示为

（2）流量守恒约束，即对于选择任意出行方式的拥有私家车客流而言，其在该出行方式不同出行路径上的客流量之和应该为其总量，同理选择任意出行方式的非拥有私家车客流量也应该等于其在该出行方式不同出行路径上的流量之和，该约束可分别表示为

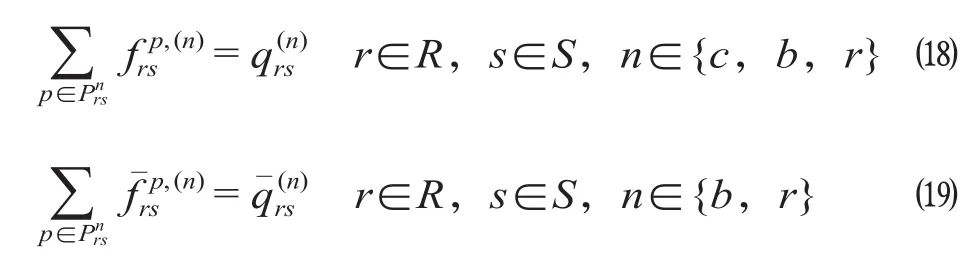
（3）变量非负约束，即选择各交通出行方式的OD流量以及各出行路径上流量必须非负，该约束可表示为

3 算法设计

为了实现以上双层规划模型的求解，设计一种模拟退火-遗传算法和Method of Successive Averages(MSA)算法相结合的混合算法，其中，模拟退火-遗传算法用于求解上层规划模型，即城轨列车运行计划与票价优化模型以得到轨道交通网络各线路列车运行计划、快车票价方案(若开行快车)；而MSA算法用于求解基于给定城轨列车运行计划与票价组合方案的下层规划模型，即多类客流多方式出行交通均衡分配。下层规划模型求解出客流分配结果后，又反作用于上层规划模型作为评估种群个体适应度的输入数据。通过上下层规划间的交替调整，直至目标函数值在很小的范围内变化，即得到最优轨道交通各线路列车开行方案和快车票价方案。设计得到求解算法框架如图1所示。

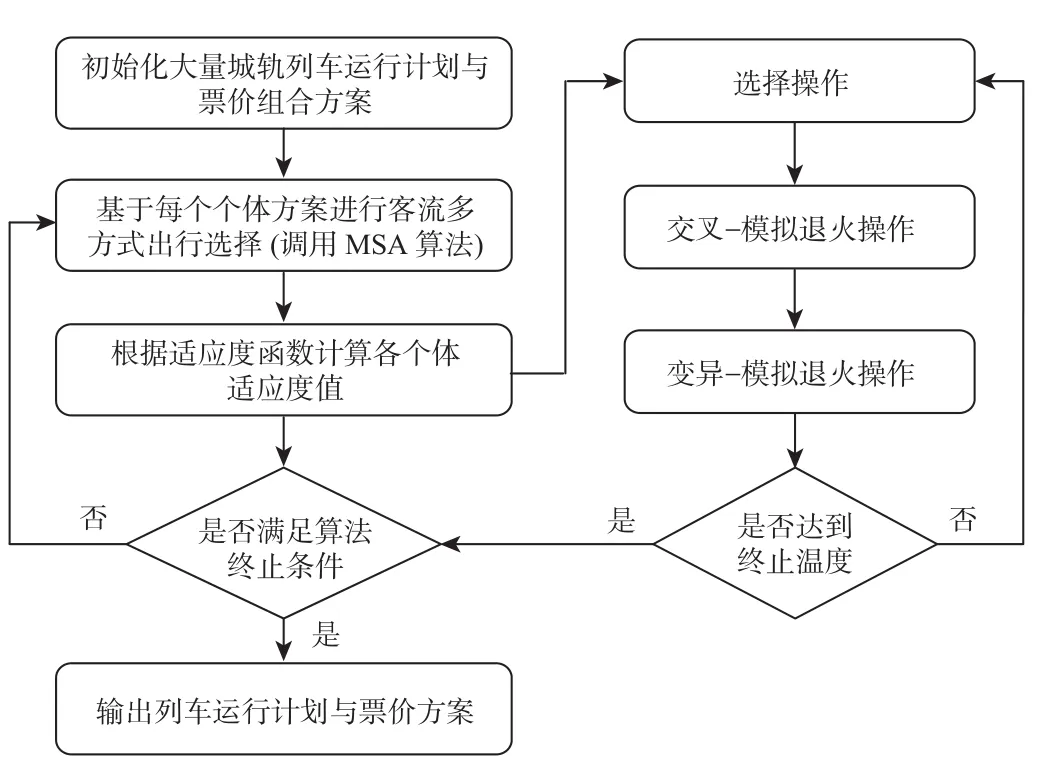
图1 求解算法框架Fig.1 Framework of solving algorithm

模拟退火-遗传算法中每个个体解采用二维二进制编码方式，每一行对应一个线路方向，其编码内容包括5部分：是否开行快车、快车停站方案、快车发车数量、慢车发车数量、快车票价，其中每一行5部分内容二进制编码长度分别为1，K，6，6，4。在模拟退火-遗传算法种群进化过程中，选择操作采用轮盘赌方式，即按照个体被选中的可能性与该个体适应值成正比的方式进行选择，对选择的个体分别进行交叉与变异操作。

（1）遗传交叉算子。交叉操作采用两点交叉方式，在交叉过程中引入模拟退火思想以一定概率接收劣解，即根据两父代i，j的适应度fi，fj以及交叉后产生的两子代i′，j′的适应度fi′，fj′，计算父代与子代之间的适应度差值 Δf=fi′+fj′-fi-fj。若Δf＞ 0，则将两子代替代两父代加入到种群中；否则以概率eΔf/Tk(Tk为当前温度)接受两子代，并替换两父代。

（2）遗传变异算子。变异操作采用多点变异方式，同样期间以一定概率接收劣解，即根据父代i的适应度fi和通过变异产生的子代i′的适应度fi′计算适应度差值 Δf=fi′-fi。若 Δf＞ 0，则接受子代i′代替父代i加入种群；否则以概率eΔf/Tk接受子代。

（3）MSA算法。为了计算每个个体的适应度，采用MSA客流分配方法确定客流在由常规公交网络、道路网络与城市轨道交通网络构成的综合网络的出行方式与路径选择，具体实现步骤如下：①为综合网络上每个OD客流，生成候选出行路径集合；②搜索各OD出行最短路径，将其客流量分配到各出行方式及其相应路径上，并计算各出行方式最短路径包含路段或者区间的客流量；③基于当前路段与区间客流量更新下相应出行费用，重新计算各出行方式出行效用，并计算其分担量，并分配到各出行方式最短路径上；④更新路径、路段、区间客流量，判断前后迭代流量差是否满足收敛条件，或者迭代次数达到最大值，若是，则停止迭代输出各出行方式分担客流量及其各路径出行量，否则跳至步骤③。

4 算例分析

选择由道路网络、9条常规公交网络以及3条城轨线路网络构成的城市综合出行网络作为算例分析，算例示意图如图2所示。3条城轨线路的起点站分别为1，4，13；终点站分别为33，35，22。假定该3条城市轨道交通线路均仅开行长交路列车，即从线路一端点站开往另一端点站，且每条线路均允许开行快慢车，但其票价并不相同。通过开行高服务的快车有利于吸引拥有私家车客流选择城轨出行，并通过提高票价来避免非拥有私家车客流(期望其优先选择慢车出行)来挤占快车能力。

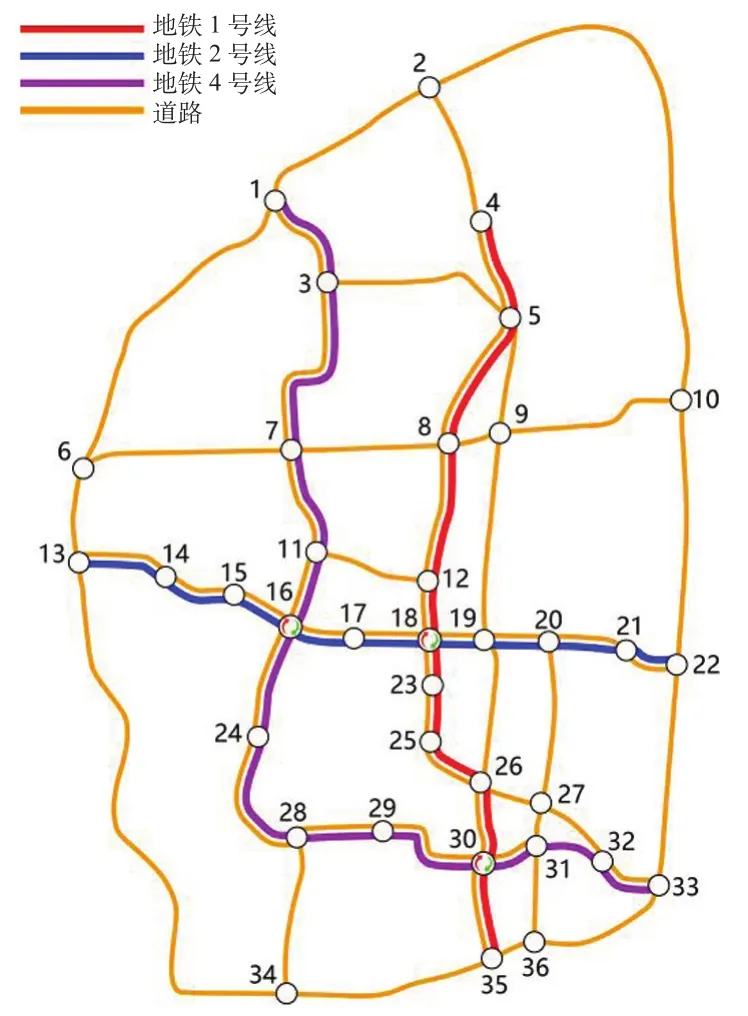
图2 算例示意图Fig.2 Schematic diagram of examples

选取早高峰小时7 : 00—8 : 00为作为本算例优化时段，共有29×29个OD对出行客流，假定各OD拥有与非拥有私家车客流需求比例关系为1 : 3，其中拥有私家车客流的出行时间价值为80元/h，而非拥有私家车客流的出行时间价值为50元/h。对于任意OD采用私家车出行而言，其单位里程燃油费与折旧费分别为1元与0.8元，平均停车费用为10元。对于采用公交车出行，旅客的平均等车时间与票价分别为10 min与2元，若存在换乘，其平均换乘时间为15 min。对于地铁出行而言，其平均步行到站点的时间为10 min，而等待时间、换乘时间等取决于待优化的线路列车运行计划。

根据以上输入数据与参数，利用计算机编程实现上述求解算法，获得各线路列车运行计划与票价方案如表1所示。由表1数据可知，3条城轨线路均开行快车，但其开行数量相对较少，这主要是客流选择中私家车客流量相对较少，不应开行过多快车。另外，每条线路上下行快车的停站也存在很大差异，主要是因为在早高峰上下行OD客流并不对称。

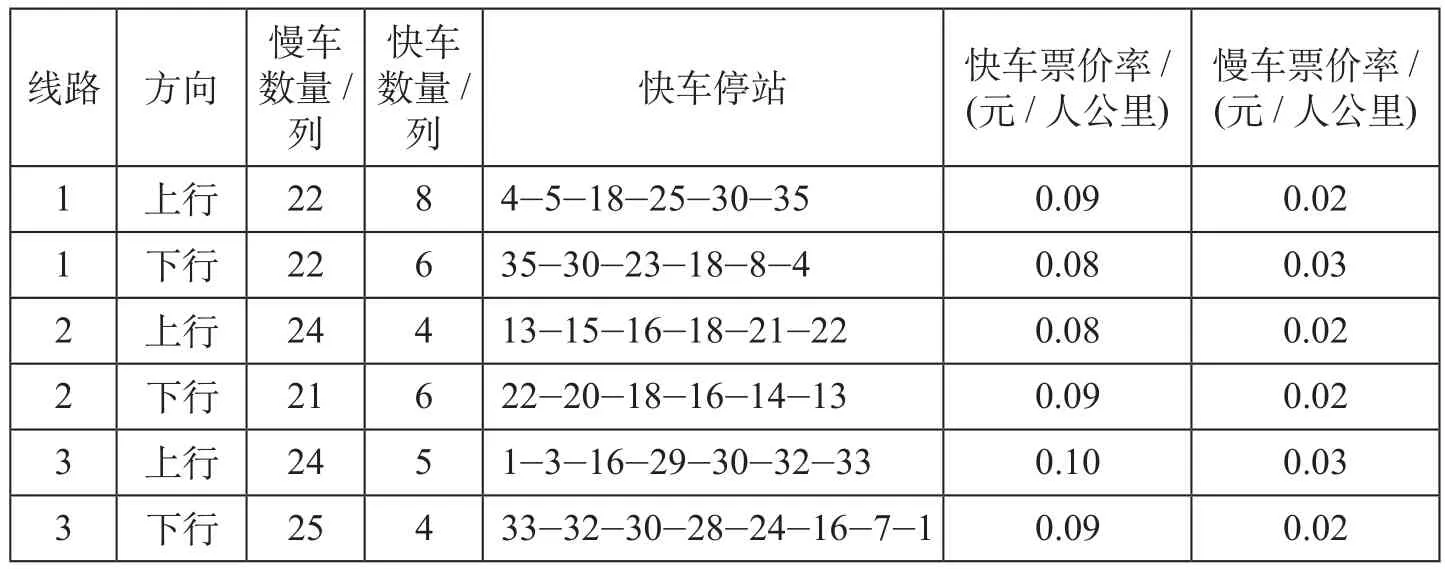
表1 各线路列车运行计划与票价方案Tab.1 Train operation plan and fare plan of each line

为了分析城轨各条线路的开行列车数量以及票价率大小对城市出行客流选择私家车、常规公交以及城轨出行的影响，得到3条线路方向平均开行列车数量对各交通方式客流分担率影响如图3所示，平均票价率对各交通方式客流分担率影响如图4所示。

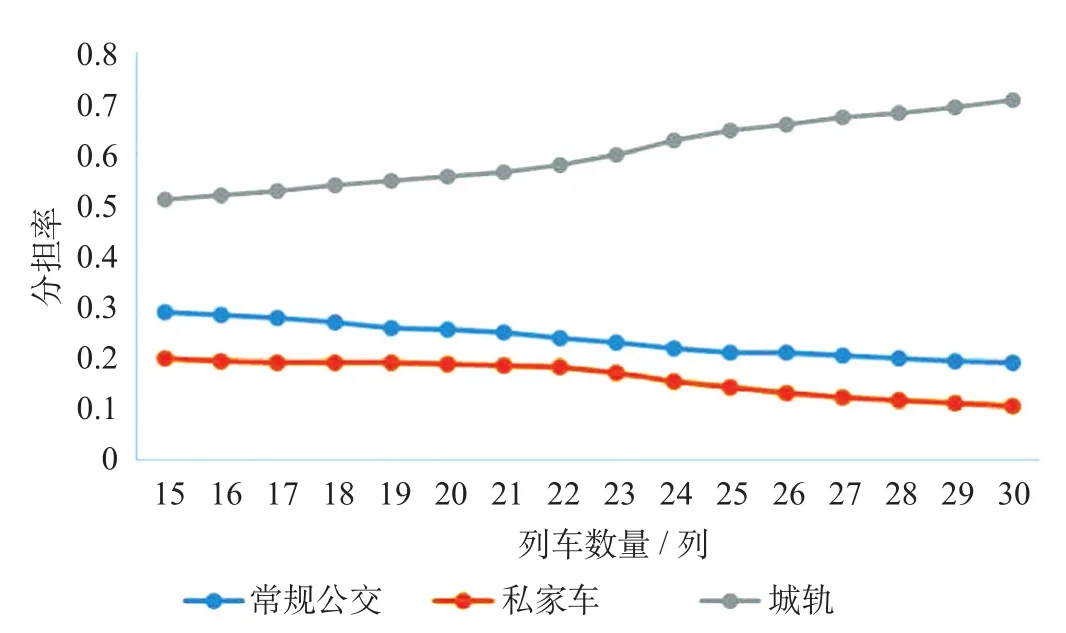
图3 线路方向平均开行列车数量对各交通方式客流分担率影响Fig.3 Influence of the average train number of rail lines on the passenger flow sharing rate of different travel modes

由图3和图4所展示的分担率变化规律来看，在道路与常规公交服务水平不变的前提下，随着城轨线路方向平均开行列车数量从15列增加到30列，选择常规公交与私家车出行的分担率都有不同趋势的下降，降低幅度均为10%左右，而选择城轨出行的客流分担率有明显的上升，从0.5上升到0.7左右，上升幅度达到20%。值得说明的是私家车客流出行分担率在前部分变化不大，主要是因为服务的提高还不足以吸引私家车客流选择城轨出行。同样，当票价水平从0.025增加到0.1时，由于城轨服务水平的下降，将导致更多客流选择私家车与常规公交出行，导致城轨客流分担率从0.7降低至0.5左右，相应地常规公交与私家车客流分担率将分别从0.19与0.09上升到0.28与0.19。由此可见，城轨列车运行计划与票价水平对城市客流出行方式选择具有较大影响，能够显著影响轨道交通、常规公交以及私家车出行分担率。

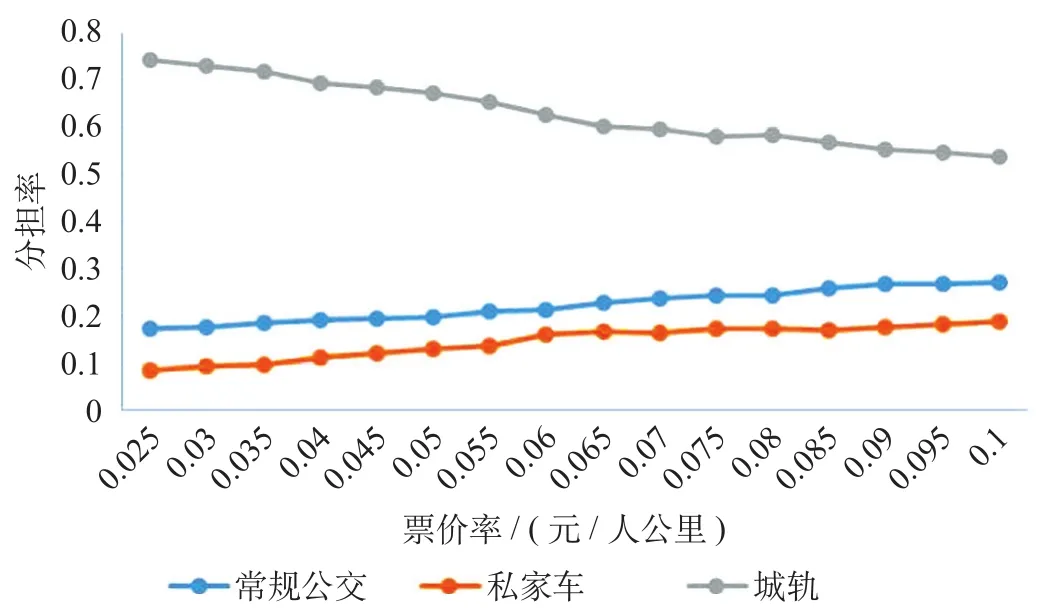
图4 平均票价率对各交通方式客流分担率影响Fig.4 Influence of the average fare rate of rail lines on the passenger flow sharing rate of different travel modes

5 结束语

通过分析拥有与非拥有私家车客流选择各出行方式出行费用的基础上，构建城轨列车运行计划与票价组合的双层规划模型，并设计一种模拟退火-遗传算法和MSA算法相结合的混合算法进行求解，研究表明城轨线路列车开行数量增加与城轨票价率的降低均能大幅度影响到选择城轨、常规公交与私家车出行客流量。由于研究中假定常规公交的服务能力与服务水平固定不变，后续可将公交线路与发车频率优化与城轨列车运行计划优化相结合，以更好改善城市多种交通方式出行服务。