缓速器传动油热物理特性仿真

刘 林，褚亚旭，吕金贺，孙文鹏

(1.北华大学机械工程学院，吉林 吉林 132021；2.北华大学土木与交通学院，吉林 吉林 132013)

随着经济的发展，重型商用车的应用越来越多，给行驶安全提出了更高要求.由于具有制动转矩大，制动平稳，噪声低等优点，液力缓速器被广泛应用于商用车[1-2].目前，国内对液力缓速器的研究主要集中在结构参数优化、内流场流动特性等方面[3-10].此外，袁哲等[11]分析了不同叶片倾角的液力缓速器温度场，张孟锋等[12]分析了液力缓速器制动转矩的影响因素.液力缓速器传动油的物理特性是制动转矩的影响因素之一，目前，大多假设传动油的物理性质不变研究缓速器内流场，而在实际中，传动油的物理性质会随着工作腔的温度变化而发生动态变化，进而对制动转矩产生影响.因此，研究液力缓速器传动油的热物理性质可以为制动转矩预测提供参考.本文通过计算流体力学(CFD)技术开展传动油热物理性质对液力缓速器制动性能的影响研究.

1 传动油热物理性质

液力缓速器传动油可以将机械能转化为热能，其功能决定传动油必须具备特定的物理性质.为适应复杂工况，应保证具有良好的环境适应性，低温时保持良好的流动性，高温时具有稳定性.液力缓速器传动油的动力黏度、密度和比热容3个物理性质受温度影响.因此，本次开展变温条件下传动油动力黏度、密度和比热容的变化规律研究.各物理性质测定方法：利用旋转式黏度计测定传动油动力黏度，在标准大气压下，将传动油加热至110 ℃，记录不同温度下的动力黏度；通过密度计，利用恒温水浴法测定传动油密度；在密闭条件下，将氮气作为保护气体，用差示扫描量热仪测量温度从0 ℃升至130 ℃的比热容.通过多项式拟合绘制拟合曲线，得到传动油动力黏度、密度和比热容与温度的关系，见图1.由图1可见：动力黏度、密度与温度负相关，比热容与温度正相关.动力黏度随温度的升高而降低，20～60 ℃下降较快，60～100 ℃下降较慢.密度与温度呈线性相关，动力黏度、比热容与温度呈非线性.

图1 传动油物理性质与温度关系Fig.1 Relationship between physical properties of transmission oil and temperature

通过曲线拟合得到3个关系式：

fμ(θ)=-0.000 000 903θ3+0.000 208 9θ2-0.015 95θ+0.412 9，R2=0.992 4，

(1)

fρ(θ)=-0.621 2θ+885.3，R2=0.999 9 ，

(2)

fc(θ)=0.000 388 3θ3-0.078 95θ2+7.216θ+1 893，R2=0.992 6 ，

(3)

式中：fμ为传动油动力黏度(Pa·s)；fρ为传动油密度(kg/m3)；fc为传动油比热容[J/(kg·℃)]；θ为传动油温度(℃)；R2为拟合优度，越接近1拟合程度越好.将温度代入式(1)、(2)、(3)得到在该温度下传动油的动力黏度、密度和比热容.

本文采用CFD分析方法研究液力缓速器在转速为1 200 r/min时动力黏度、密度、比热容与制动转矩的关系，探究传动油动力黏度、密度、比热容对缓速器性能的影响，解析传动油实时变化与制动性能的关系.

2 CFD数值计算

2.1 控制方程

传动油在缓速器内部的流动为非稳态不可压缩的黏性流动，需要遵守质量守恒方程和动量守恒方程.考虑温度的影响，在使用Fluent软件时，需开启能量方程[13].控制方程如下：

质量守恒方程

式中：ρ为工作介质密度；ui为空间3个方向上的速度；xi为3个坐标中的1个，i为轮换指标，指空间中的3个方向.

动量守恒方程

(4)

式中：t为时间；p为静压；τij为应力张量；uj为空间3个方向速度；xj为3个坐标中的1个，j为轮换指标，指空间的3个方向；gi为i方向上的重力体积力；Fi为i方向上的外部体积力.

能量守恒方程

式中：E为单位质量流体内能；u为传动油速度；Sh为所有体积热源；∇为哈密顿算子；∇·(keff∇θ)为传导引起的能量传递，keff为有效热传导率.

图2 液力缓速器流道提取及网格模型Fig.2 Flow channel extraction and mesh model of hydraulic retarder

2.2 仿真计算模型与假设

液力缓速器流道提取及网格模型见图2.选取整个流道作为计算域，转子循环圆半径为146.5 mm，定子循环圆半径为148 mm，转子叶片36个，定子叶片34个，叶片倾角42°，叶片楔角30°.采用适用性较强的T/Grid网格技术划分网格[14].将网格导入Fluent中进行数值计算.对液力缓速器的热物理性质进行数值计算时采用RNGk-ε湍流模型，假定液力缓速器定子和转子以及叶片在工作时不发生变形.进口边界条件设置为速度进口，进口温度设置为60 ℃；出口设置为自由出流.假设壁面不会与外界换热，设置成绝热壁面.采用比SIMPLE收敛速度更快的SIMPLEC算法，通过改变传动油物理性质及转速对缓速器进行数值模拟.

液力缓速器转矩计算经验公式为

式中：λB为制动转矩系数；g为重力加速度；nB为缓速器转子转速；D为循环圆有效直径.

3 数值计算结果与分析

3.1 动力黏度与制动转矩关系

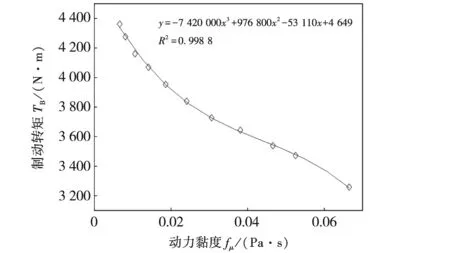
图3 动力黏度对制动转矩的影响Fig.3 Effect of power viscosity on braking torque

动力黏度对制动转矩的影响见图3.由图3可见：制动转矩随动力黏度的增大而逐渐减小.这是因为，随着动力黏度的增大，流道内的流体速度逐渐减小，导致转子叶片压力减小，由于液力缓速器的制动转矩由转子受到的压力决定，因此，制动转矩降低.对仿真计算得到的制动转矩结果进行拟合可见，制动转矩与动力黏度近似为三次函数关系.

图4为不同动力黏度下流道截面速度矢量图(流道截面切割方式见图2).为了便于分析，调整流道截面的显示角度，使流道截面上方为动轮区域，下方为定轮区域.由图4可见：在不同动力黏度下的流道截面速度矢量图分布规律相同，离心力使液力缓速器工作腔内流场形成了高速区域A(转子出口、定子入口)与高速区域C(定子出口、转子入口).传动油在动轮带动下获得动能进入定轮，在右侧形成高速区A，进入定轮后由于壁面影响致使速度下降(B).在离心力的作用下，传动油流经定子时速度逐渐增加，形成左侧的高速区C；当介质再次进入动轮时，动轮壁面阻碍介质流动，速度逐渐减小；流道中心位置存在低速涡，是由低速油液从入口流入所致.3种动力黏度对应的最大速度分别为60.8、80.2、106.0 m/s，随着动力黏度的减小，传动油流速呈现增大趋势.

图4 流道截面速度矢量Fig.4 Velocity vector of flow channel section

图5 密度对制动转矩的影响Fig.5 Influence of density on braking torque

3.2 密度与制动转矩关系

密度对制动转矩的影响见图5.由图5可见：随着密度的增大，制动转矩与密度近似线性正相关.由液力缓速器转矩计算经验公式可知，密度与制动转矩成正比，与仿真结果相同.当工作介质密度变大时，其单位体积总动能增加，转子叶片所受压力增加，导致制动转矩增大.

图6为不同密度流道截面的压力云图.由图6可见：截面压力分布趋势基本一致，由内向外呈带状分布并逐渐增大，由于涡流的影响，截面中心产生低压区.不同密度下的最大静压依次为2.62、2.43、2.38 MPa.可以看出，随着密度的减小，截面最大正压有减小的趋势.

图6 流道截面压力Fig.6 Pressure cloud of flow channel section

3.3 比热容与制动转矩关系

比热容对制动转矩的影响见图7.由图7可见：随着比热容的增加，制动转矩变化并不明显，比热容和制动转矩弱相关.比热容对温度的影响见图8.由图8可见：随着比热容的增加，温度有下降趋势，进而影响动力黏度与密度，说明比热容通过影响工作腔温度影响缓速器的制动性能.

3.4 动态仿真分析

通过两种方案对比分析恒物性和变物性：方案1，液力缓速器传动油的物理性质恒定，不同转速下的物理性质不变，简称其为恒物性；方案2，在仿真过程中，液力缓速器传动油的物理性质随着仿真计算的进行自动调节，简称变物性，该方案通过自定义函数(UDF)将传动油物理性质随温度变化的表达式导入Fluent软件，在仿真计算过程中，动力黏度、密度、比热容的数值将根据温度自动调节.

通过监视出口温度得到转速与温度的关系，见图9.由图9可见：传动油温度随着转速的升高而升高.由于动力黏度、密度、比热容对温度比较敏感，其数值也会处于动态变化状态，进而影响缓速器的制动性能，因此，传动油的动力黏度、密度、比热容变化在仿真过程中不可忽略.

图7比热容对制动转矩的影响Fig.7Influence of thermal capacity on braking torque图8比热容对温度的影响Fig.8Influence of specific heat capacity on temperature图9传动油温度与转速的关系Fig.9Relationship between transmission oiltemperature and speed图10恒定物性与变物性仿真结果对比Fig.10Simulation results comparison of constantand variable nature

由图10可见：变物性(方案2)仿真计算得到的制动转矩比恒物性(方案1)得到的制动转矩小，这是因为在进行仿真时假设物性不变(fρ=876 kg/m3，fμ=0.009 Pa·s)，然而，传动油的温度会随转速的增大而升高；在同一转速时，不同部位的温度也会存在差别.传动油的物理性质随着温度的改变而变化，方案1的物理性质与方案2的物理性质是不同的，得到的制动转矩也不一样.如表1所示，恒定物性与变物性间的误差最大为10.34%，最小为2.89%.转速为600～1 100 r/min时，相对误差随着转速的增大而下降；1 100～1 200 r/min时误差随转速增大而上升.

表1 恒物性和变物性间的误差Tab.1 Error of constant and variable

图11为R(与液力缓速器循环圆同圆心的弦面半径)为90、110、130 mm时的弦面涡量分布图.由图11可见：两种方案的涡量分布大致相同，分布在叶片周围，在叶片楔角处涡量较大；R为90 mm时的涡量要大于R为110 mm和130 mm时的涡量.此外，由于转子转动使转子区域的涡量高于定子区域(上方为转子，下方为定子)；方案2的涡量略小于方案1的涡量，这是由于温度升高导致动力黏度减小，使油液与壁面之间的黏性阻力减小，导致涡量减少，消耗能量降低.因此，方案2的制动转矩小于方案1.

图11 弦面涡量分布Fig.11 Chord vorticity distribution

4 小结与讨论

本文研究了动力黏度、密度和比热容与温度的关系，通过拟合得到表达式；分析了传动油物理性质变化对制动性能的影响；对传动油变热下的液力缓速器内流场进行了仿真计算.结果表明：动力黏度和密度随温度升高而减小，比热容随温度升高而增大；制动转矩随动力黏度减小而增大，与密度呈正相关，比热容对制动性能的影响较小.

本文研究了传动油热物理性质对液力缓速器的影响，使用自定义函数进行了动态仿真，可为后续液力缓速器制动转矩的预测提供参考.但本文仅研究了传动油热物理性质对液力缓速器制动转矩部分内流场的影响，未深入研究对其他内流场的影响，未来将深入进行综合分析.目前，对更高制动转矩和更低空转功率损失的液力缓速器需求极为迫切[15]，下一步也将重点开展降低液力缓速器空转功率损失的研究.