多孔介质热弥散系数的分形模型*
张 杰,张 赛,高伟业,胡世旺,汪振毅
(昆明理工大学 机电工程学院,昆明 650500)
引言
多孔介质的热质传递过程具有广泛的实际应用背景,其传递的重要特征之一就是通过热弥散效应增强传递过程[1-5].Jouybari 等[6]认为多孔介质中流体流速较高时,弥散效应不可忽略.Vadasz [7]通过数值模拟研究了流体弥散效应,但没有具体分析流体弥散效应的影响因素.戚涛等[8]基于孔隙网络模型中的流动模拟,采用Euler 描述方法描述了多孔介质中流体速度分布情况,证实了多孔介质内流体速度的脉动情况.但是Euler 描述法很难精确地描述流体质点的运动过程,弥散效应是由于孔隙中流体速度脉动引起的,这种脉动类似于湍流脉动,存在一定的误差.对于热弥散系数的研究,研究者们试图建立统一适用的热弥散系数模型,如Moyne 等[9]采用体积平均方法得到了均质多孔介质内宏观热弥散系数单方程模型.但该模型是基于空间周期性结构得到的,实际多孔介质并不是简单的周期结构,这使得该模型缺乏通用性.Hunt 等[10]利用统计平均的方法和混合长度理论提出了中心区和近壁区热弥散效应的关系式,并根据他们自己的试验数据确定了其中的经验常数,但这些经验常数的物理意义并不明确.以上研究者所建立的热弥散系数关系式具有很大差异,模型之间缺乏通用性和可比性;此外,在多孔介质热弥散系数的研究中,很少对速度脉动做详细的解释说明.因此,有必要进一步理论研究多孔介质流动过程的热弥散效应.
本文通过对流体在多孔介质中的流动特征分析,计算得到了流体在湍流和层流的临界状态时的截面速度关系式,分析此过程中流体在孔喉结构处的局部水头损失,推导了速度弥散效应关系式,并结合速度弥散效应关系式、分形理论、孔喉结构随机分配函数,建立了热弥散系数模型.该模型把热弥散系数与孔隙率、孔喉比、孔道特征长度、固体颗粒直径、迂曲分形维数和面积分形维数联系起来,减少了模型中的可调参数.最后,详细解释了孔隙结构参数对热弥散系数的影响.
1 孔喉结构分布特征

2 孔喉结构流动特征
2.1 孔喉结构流动模型
对于颗粒填充床、多孔岩石和土壤等颗粒型多孔介质,其内部孔道存在孔喉结构.孔道内流体流动状态受孔道结构影响,流体在孔道内的流动规律随孔道结构的变化而变化.孔道的扩张和收缩由直径不同的固体颗粒引起,固体颗粒凸起在孔道中形成大小不同的孔喉结构,这些孔喉结构连接在一起形成弯曲的孔道.
如图1所示,LBF为喉道直径,m;LBF+dp为孔道直径,m.图中虚线框表示一个孔喉单元,其孔隙率为
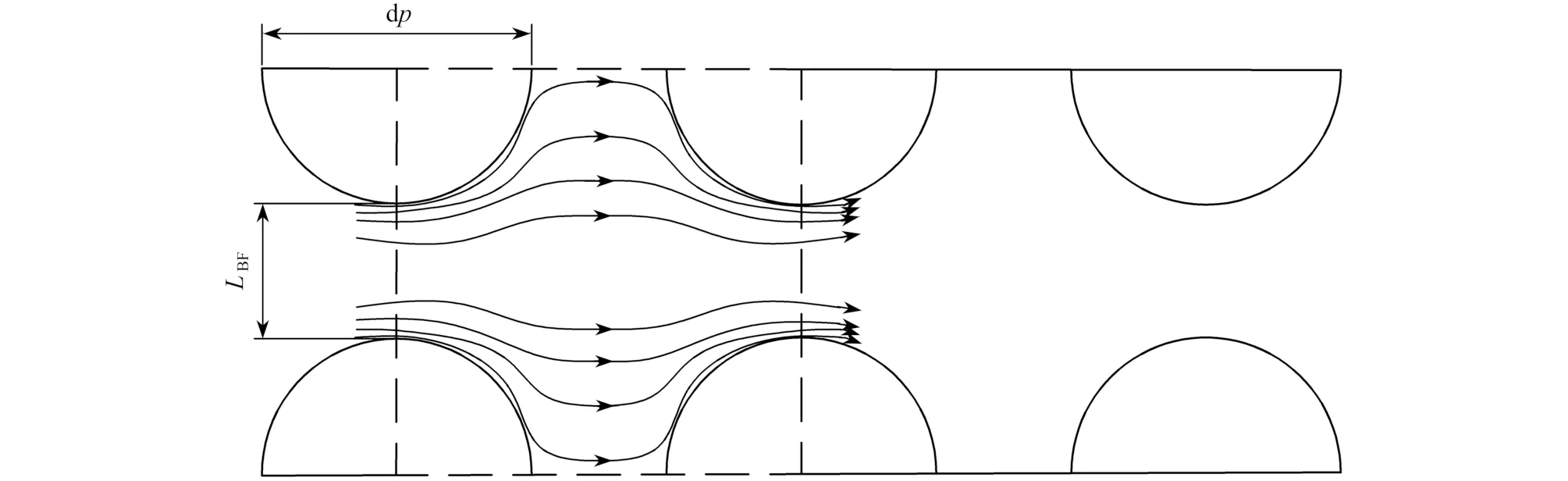
图1 孔喉结构流动模型Fig.1 The flow model for the pore-throat structure

式中,dp表示固体颗粒直径,m.
孔喉比表示为

式(6)表明,喉道直径一定时,固体颗粒直径越大,孔喉比越大.
2.2 局部水头损失分析
局部水头损失为因孔道形状发生突变而使流体速度大小和方向发生改变时流体的能量损失.假设一个孔喉单元内固体颗粒直径相等,流体以层流状态由孔喉结构的左端流入右端流出时,流体运动状态发生改变,形成紊流状态.流体经过l段长度后恢复到层流状态,由于l段长度很短,所以沿程损失可以忽略,局部水头损失占主导地位.
图2 为存在孔喉结构的孔道简化图,流体以一定的速度在孔道中流动,在孔道扩张和收缩处由稳定的层流状态变为紊乱的湍流状态.图中l段表示由湍流状态到层流状态的流体所经过的长度,称为Prandtl 混合长度.混合长度所受各力沿流动方向的合力可表示为
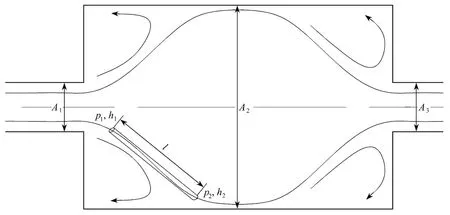
图2 孔道内流体流动模型Fig.2 The fluid flow model in the channel

式中,P1和P2为沿流动方向的压强,Pa;ρ 为流体密度,kg/m3;g为重力加速度,g=9.8 m/s2;r为混合长度的半径,m;l=ky为Prandtl 混合长度,m;k为Karman 常数,一般取0.4;y为距离孔道壁面的距离;τ 为黏性切应力.
黏性切应力表示为

式中,µ为流体黏度,Pa·s;vτ为流体速度,m/s.

2.3 弥散效应


3 热弥散系数的分形模型


4 分析和讨论
本文中的流体为氢气,分析氢气在多孔介质中流动情况,模型中的部分参数取值如表1所示.图3 为式(26)与文献[14]结果的对比,可以看出一致性较高.从图中可以看出,随着孔隙率的减小,热弥散系数迅速增大.这是因为孔隙率越小,流线越弯曲,速度弥散效应越强,所以导致热弥散系数越大.
图4 为热弥散系数分形模型与Metzger 等[15]的实验值对比图.Metzger 等[15]以水为流体,实验预测了玻璃球填充床内水的热弥散系数.由图可知,本文的热弥散系数分形模型与实验值吻合度较高.由图还可知,随着Berkeley 数的增大,热弥散系数增大,即流体流速越快,热弥散系数越大.这是因为流体流速变快时,弥散效应加强,所以热弥散系数增大.
图3 和图4 表明,式(27)可用于计算颗粒填充床、多孔岩石和土壤等具有孔喉结构的多孔介质内流体热弥散系数.
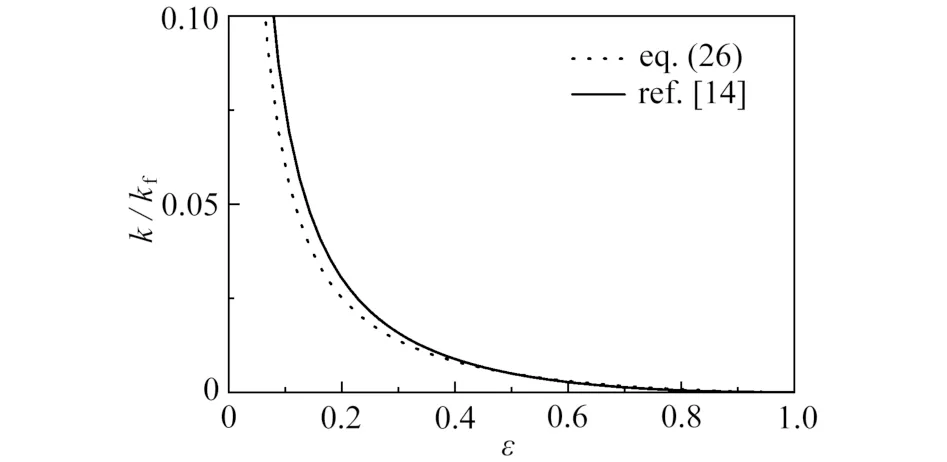
图3 热弥散系数分形模型与常规模型对比Fig.3 Comparison between the fractal model for the thermal dispersion coefficient and the conventional model
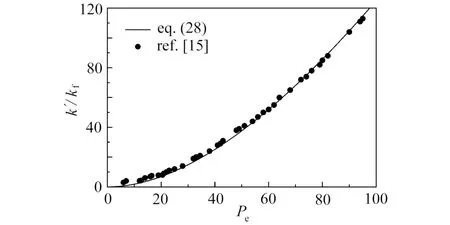
图4 热弥散系数分形模型与实验值对比Fig.4 Comparison between the fractal model for the thermal dispersion coefficient and experimental values
将表1 中数据代入关系式(22)和(27)中,得到流体物性、孔隙结构参数与热弥散系数的函数关系,图5~8 能够较准确地解释孔隙结构参数对热弥散系数的影响.

表1 分形模型中部分参数与数值Table 1 Some parameters and values in the fractal model
图5 显示了速度弥散效应随孔喉比的强弱变化情况.由图可知,迂曲分形维数为1.1,1.2 和1.3 时,随着孔喉比的增大,速度弥散效应逐渐增强,孔喉比增大到150 时,孔喉比对速度弥散效应影响较小.这是因为孔喉比增大时,流体由层流转变为湍流,由式(22)可知,速度大小以孔喉比的次方数倍关系偏离其速度原有平均值;当迂曲分形维数增大时,速度弥散效应增强,即孔道越迂曲,速度弥散效应越显著.
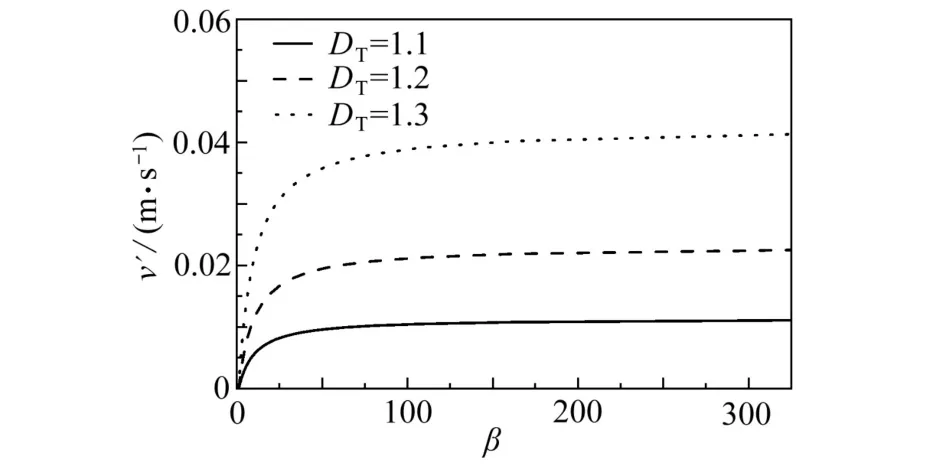
图5 孔喉比对速度弥散效应的影响Fig.5 Influences of the pore-throat ratio on the velocity dispersion effect
图6 为面积分形维数对热弥散系数的影响曲线.从图中可以看出,热弥散系数随面积分形维数的增大而减小,面积分形维数增大意味着固体颗粒在孔道空间的占比减小,导致流体流动时局部水头损失系数减小,速度弥散效应减弱,热弥散系数越小.

图6 面积分形维数对热弥散系数的影响Fig.6 Influences of the area fractal dimension on the thermal dispersion coefficient
图7 为迂曲分形维数对热弥散系数的影响曲线,随着迂曲分形维数的增大热弥散系数显著增大.由于孔道的扩张和收缩,流体从层流状态变为湍流状态,DT越大表明孔道越弯曲,孔道弯曲使原本的紊流状态加剧,所以热弥散系数增大.
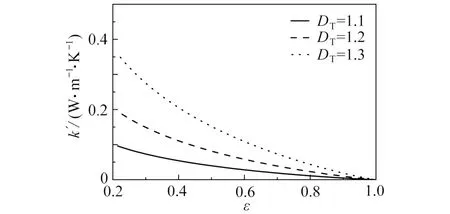
图7 迂曲分形维数对热弥散系数的影响Fig.7 Influences of the tortuous fractal dimension on the thermal dispersion coefficient
图8 为孔喉结构个数对热弥散系数的影响曲线.由图可以看出,随着孔喉结构个数的增加,热弥散系数增大,其增大的趋势逐渐减缓.这是因为孔道空间被固体颗粒占据面积增大,流体通过孔道的路径变长,导致速度弥散效应增强,故热弥散系数增大;当孔喉结构个数足够多时,相当于孔喉比大于150,孔道空间被连续的固体颗粒填充,与图4 结论一致,孔喉比不再对速度弥散效应有影响,故热弥散系数变化值较小.
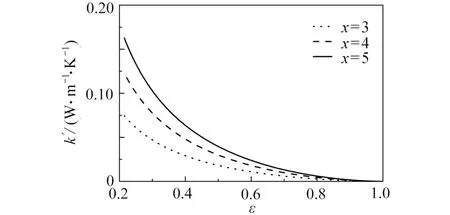
图8 孔喉结构个数对热弥散系数的影响Fig.8 Influences of the number of pore-throat structures on the thermal dispersion coefficient
5 结论
本文对多孔介质内流体进行力学分析,探究了热弥散系数与流体在多孔介质孔隙内流动的关系,得到的热弥散系数模型普适性高,建立的模型可以确定微观孔隙结构多孔介质热弥散系数,为流体在微观孔隙中的流动研究提供了理论参考.主要得出了以下结论:
1)管道形状发生突变(如扩张、收缩和弯曲)时,流体速度弥散效应增强,热弥散系数增大.
2)孔喉比为1 时,局部水头损失系数为0,热弥散系数为0;孔喉比大于150 时,孔喉比对速度弥散效应影响较小.
3)本文的热弥散系数模型是基于孔喉结构模型和速度弥散效应得到的,所考虑的参数较全面,无速度弥散效应经验参数,更精确地解释了热弥散过程.

