GARCH模型的二次加权复合分位数估计①
钟泽君, 李婷婷
西南大学 数学与统计学院, 重庆 400715
文献[1-2]提出了广义自回归条件异方差(GARCH)模型, 该模型主要用于刻画资产收益率的波动规律. 文献[3-4]将GARCH同多种传统模型进行实证比较, 结果表明GARCH能更为准确地反映我国某些市场的波动情况. 后续学者根据市场特征和需求的不同对GARCH进行了推广研究, 并演化出了一系列GARCH族模型[5].
目前, 用于估计GARCH模型参数的方法多种多样. 文献[6]将类极大似然(QML)法用于GARCH和ARMA-GARCH模型的参数估计; 文献[7]将QML法扩展到一系列多维GARCH类模型, 且实证表明其能很好地刻画汇率序列的波动. 虽然文献[8]指出QML估计对数据分布具有一定的容错性, 但其对异常值很敏感, 少量异常值就会对QML估计产生巨大的影响, 也即QML估计并不稳健, 其次, QML法还要求序列4阶矩存在, 而金融收益率时序列分布往往呈现出“尖蜂厚尾”的特点, 难以满足该条件. 由此, 文献[9]提出了较为稳健的偏差绝对值最小(LAD)法. 文献[10]提出了基于传统GARCH模型的分位数回归估计(QR)法, 并证明了该估计的一致性. 虽然QR估计一定程度上减少了数据尖峰厚尾所造成的估计误差, 但风险水平的选取将直接影响到QR估计的结果. 因此, 文献[11]将复合分位数回归(CQR)应用于估计高频数据的GARCH参数, 数值模拟结果显示CQR估计较QR估计更为精确有效. CQR通过综合考虑多个风险水平下的条件QR使得估计更为稳健有效, 但应对不同的市场损失情况应当赋予不同程度的损失, 故文献[12]考虑加权复合分位数回归(WCQR)法, 其通过极小化WCQR参数估计的渐进方差得到权重值, 对于不同分位数回归给予不同的权重, 以此得到更加稳健有效的估计.
近年来, 受文献[13]提出的两步QR思想的启发, 文献[14]提出了GARCH模型的混合QR估计, 该估计主要分为两步: 首先计算QML估计下的条件标准差拟合序列, 接着将此条件标准差拟合序列的倒数作为QR损失的权重得到估计, 数值分析表明混合QR估计可以削弱极端波动的影响, 得到更为精确有效的估计; 文献[15]还将上述混合QR估计用于探究GARCH-X误差模型, 数值模拟显示出该混合估计在大样本下表现最优. 本文进一步将混合估计扩展到CQR, 结合WCQR思想, 由此提出二次加权分位数回归(BWCQR)技术. 数值模拟及实证分析表明利用BWCQR估计GARCH模型参数在一定准则下相较已有估计技术更加合理有效.
1 模型及估计
1.1 GARCH模型的BWCQR估计
记yt表示某资产第t天的收益率, 则标准GARCH(p,q)模型为
yt=vtηt
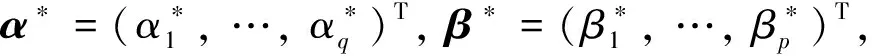
对应GARCH(p,q)模型的条件τk分位数为
(1)
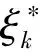
GARCH模型的CQR估计[11]为
(2)

将文献[12]提出的WCQR扩展至GARCH模型
(3)

将文献[14]提出的混合QR加权思想扩展到CQR, 由此衍生出估计
(4)
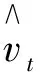
将式(3)和式(4)相整合, 即可得到本文提出的BWCQR估计
(5)
1.2 假设及定理
在给出BWCQR估计的渐进性质之前, 须引入一些记号和模型假设: 记向量a的欧几里得范数为‖a‖;C表示在不同的计算过程中不尽相同的任一正数; 定义矩阵A=(aij)的欧几里得范数为‖A‖=∑i,j|aij|;V表示一广义可积随机变量; {St}表示一平方可积非负平稳遍历过程且满足St∈Ft-1; 变量ρ满足 0<ρ<1;ρτk(u)关于u的导数为ψτk(u)=τk-I(u<0).
假设1模型的真值θ*为Θμ的内点, 其中参数空间Θμ定义为
其中实数μ∈(0, 1)且使得θ*∈Θμ.
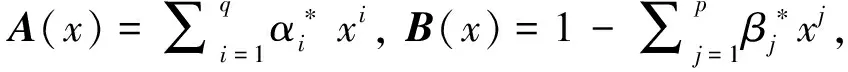
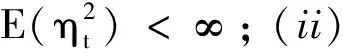
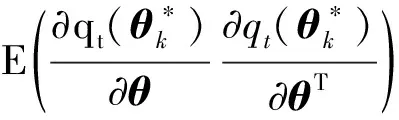

证明分别定义
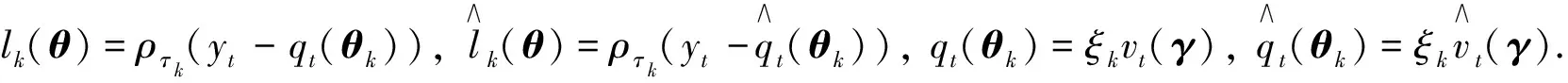
本文主要证明定理2及推论3, 定理1不作详细证明. 关于定理1可参考文献[15]中定理1的证明, 分证四点即可:
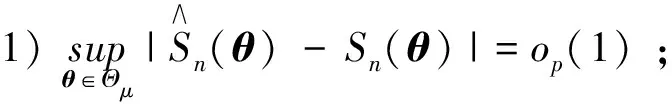
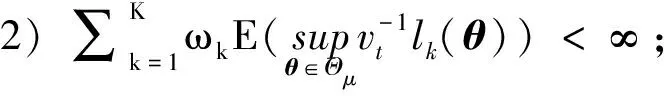
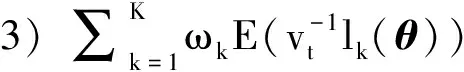
4) 对任一θ#∈Θμ, 当0时有其中B(θ#)={θ#∈Θμ: |θ#-θ|<}表示以θ#为中心为半径的邻域.

注1当K=1,ω=1且vt=1时, 定理2退化为QR估计的渐进性质, 详见文献[10]定理2; 当K=1且ω=1时, 定理2退化为混合QR的渐进性质, 详见文献[15]定理2; 当ω=1且vt=1时, 定理2退化为CQR的渐进性质, 详见文献[11]定理2.
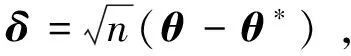

证明
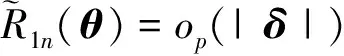

(6)
注意到, 对∀τ∈(0, 1)有ρτ(x)≤|x|. 由ρτ(x)的Lipschitz连续性及式(6), 有
(7)
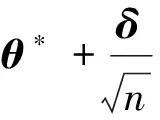
(8)
因此, 由式(8)及A.2有
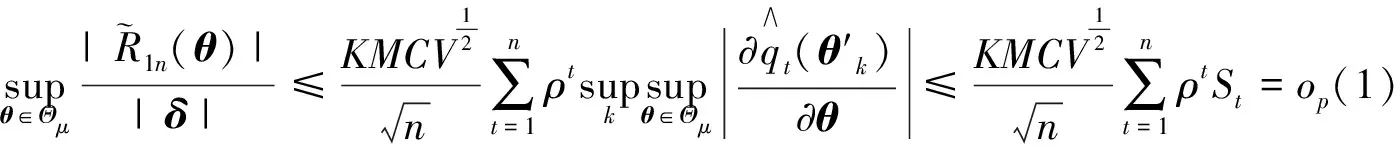
2) 定义
由文献[16]有等式
(9)
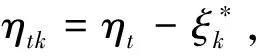
(10)
lk(θ)-lk(θ*)=dt(θk)[-ψτk(ηtk)+Btk]
(11)
据ψτ(x)的定义对其应用Fubini定理及泰勒展开有
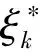
(12)

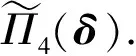
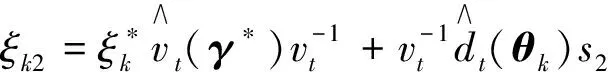
引理2在假设1-3满足的条件下, 有
证明引理2的证明同引理1的证明类似
据文献[17]定理3.1和式(9)易证K1n(δ)=op(|δ|)与K2n(δ)=op(|δ|2).
引理3在假设1-3满足的条件下, 有
其中
证明由式(9)有
(13)
对R1n(δ)泰勒展开:R1n(δ)=-δTCn-δTK3n(θ′)δ, 其中
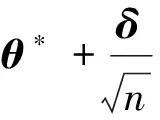
定义Btk=Btk1+Btk2, 其中
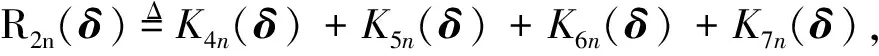
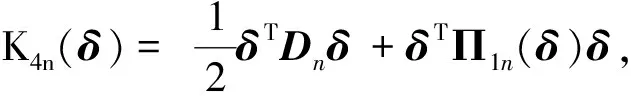
由中值定理、 文献[10]A.2及假设3, 对∀ζ>0
(14)

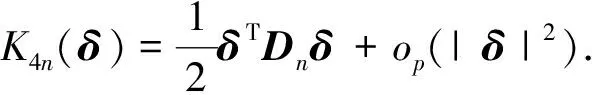
对K5n(δ)进行放缩后
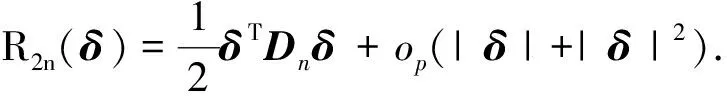
定理2证明结合引理1-3和定理1, 同文献[15]中定理2的证明类似即可证明该定理.
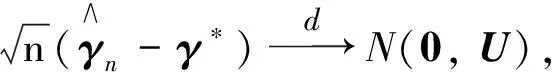
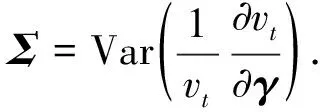
注2令
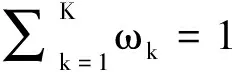
推论1证明矩阵C可分为4块分块矩阵

同样可以将矩阵D分为4块分块矩阵
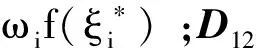
注意到, 在假设4及权重向量ω>0的条件下矩阵D,C均为严格正的可逆矩阵, 矩阵D-1CD-1的右下块(p+q)× (p+q)维矩阵U为
其中
经计算可得推论1成立.
1.3 参数估计步骤
将本文提出的BWCQR分为如下6个步骤:
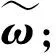
2 数值分析
2.1 蒙特卡洛模拟
基于GARCH(1, 1)模型
利用蒙特卡洛数值模拟检验本文所提BWCQR方法在有限样本下相较QML,QR和CQR方法的稳健性和有效性. 数值模拟模型参数选取如下:
(i) 分别考虑扰动项序列ηt服从标准正态分布N(0, 1),t(5)分布和t(3)分布;
(ii) 样本容量分别取n=300,500,1 000和1 500进行300次重复抽样;
(iii) 复合分位数回归模型中K值取5,9和19, QR估计的风险水平取0.3,0.5和0.7;
(iv) 本文采用估计量的偏差(Bias)、 标准差(SD)和均方误差(MSE)作为估计的评价标准.
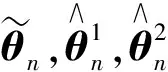
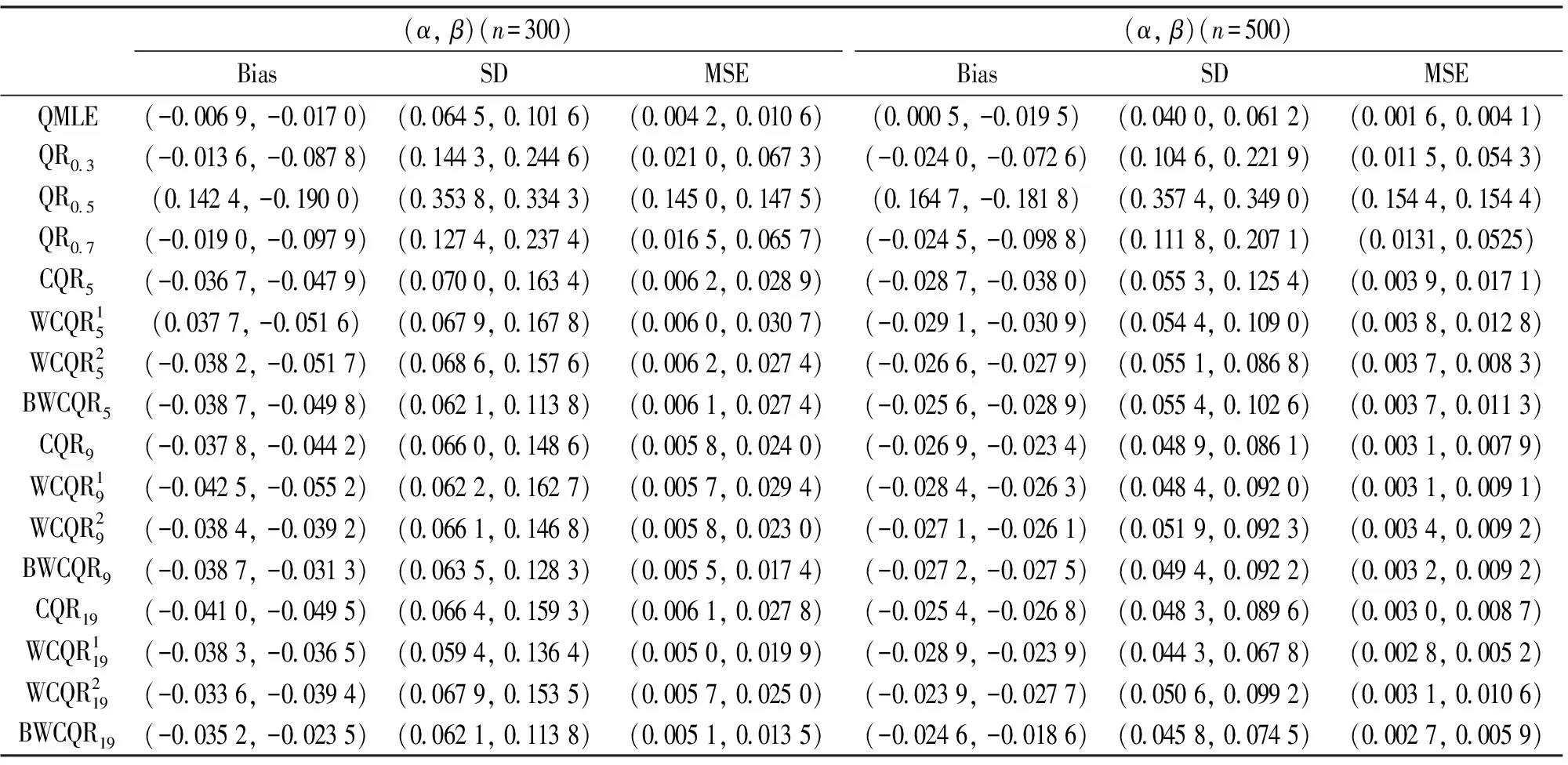
表1 GARCH(1,1)模型的不同估计的比较,ηt~N(0, 1)

续表
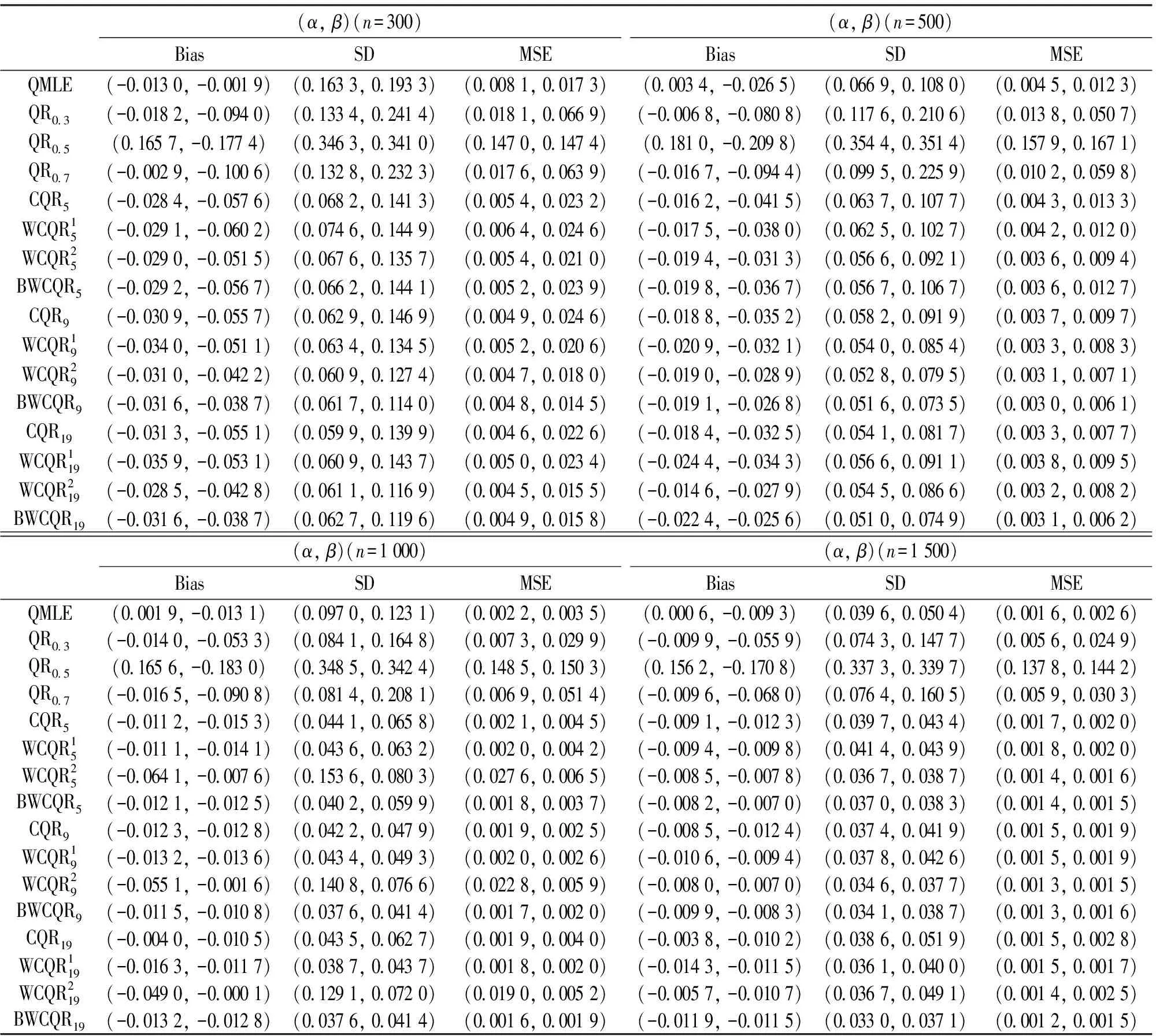
表2 GARCH(1,1)模型的不同估计的比较,ηt~t(5)
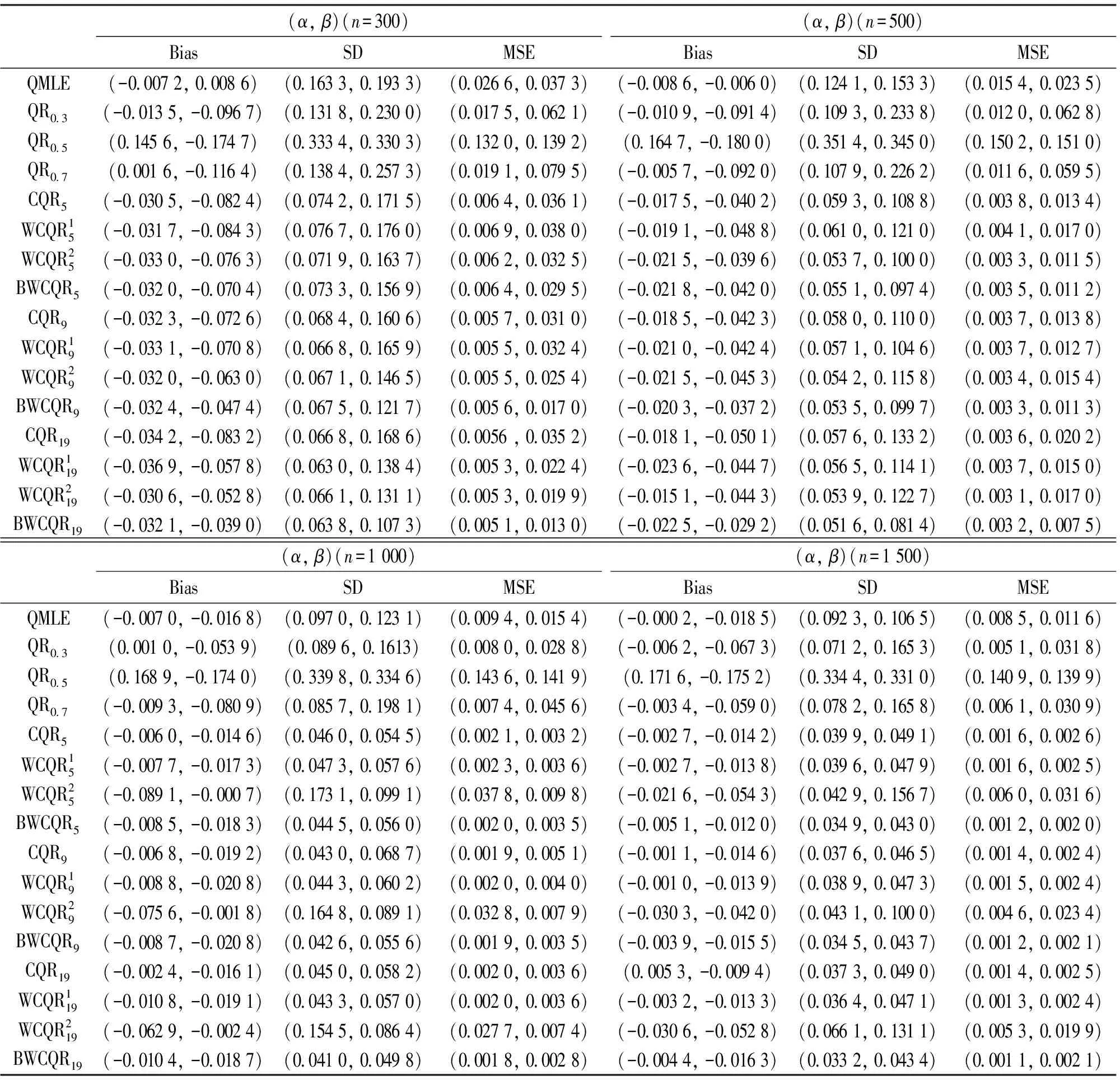
表3 GARCH(1,1)模型的不同估计的比较,ηt~t(3)
分析结果得到:
(i) 无论扰动序列的分布如何, 对任一估计, 随着样本量n的增大, MSE愈小;
(ii) 各类复合分位数估计对K值的敏感程度不强;
(iii) 样本规模n一定时,K越大, MSE越小, 也即K取19时各类复合分位数回归估计最优;
(iv) 当扰动项服从正态分布时, QMLE最优;
(v) 当扰动项服从重尾分布时, 总体而言, BWCQR估计明显优于WCQR1, 略优于WCQR2, 且随着K的增加BWCQR估计的竞争力愈强.
2.2 实证分析
选取上证和沪深300股指作为研究对象, 实证区间为2015年1月5日至2021年5月11日, 共计1 544个样本数据. 记pt为第t交易日的收盘价,rt为百倍对数收益率:rt=100×(lnpt-lnpt-1).
表4给出rt序列的描述性统计分析值. 均值大于0, 说明股指整体趋势上行, 且序列不服从正态分布、 不独立同分布. 综上所述, 足以表明rt序列具有典型的高峰厚尾特征. Ljung-Box检验Q统计量和ADF检验表明序列具有明显的长记忆性且平稳.

表4 股指收益率序列描述性统计信息
本文选用GARCH(1, 1)对该时间序列进行建模分析, 采用向前一步滚动窗口预测方法, 并将2015年1月5日至2020年1月23日作为初始滚动窗口. 本文对rt分别采用QMLE, MLE-t和BWCQR19进行拟合, 对应标准化残差序列的ARCH-LM检验通过率列于表5. 表5结果符合数值模拟结论, BWCQR估计明显优于QMLE和MLE-t.

表5 标准化残差序列的ARCH-LM检验通过率
进一步, 上证指数全序列和沪深300股指全序列在BWCQR估计下的标准化残差序列的自相关(ACF)图和偏自相关(PACF)图, 如图1,2所示, 可见BWCQR估计下股指的标准化残差序列是白噪声序列, 这再次验证了BWCQR估计的优良性.
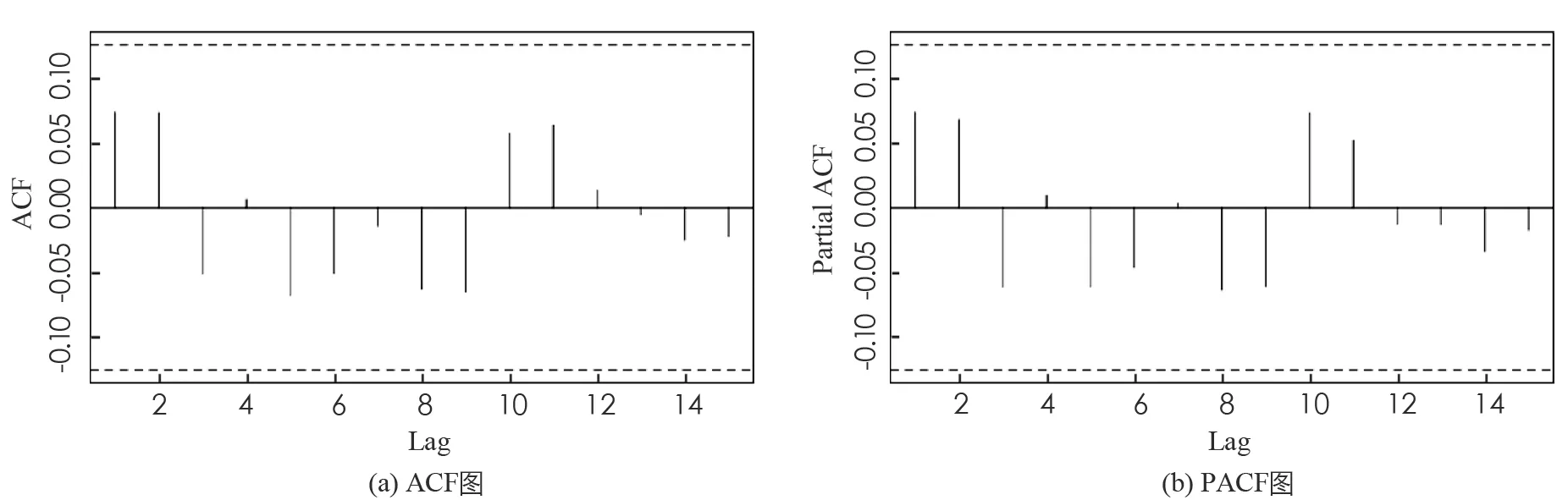
图1 BWCQR估计下上证股指标准化残差序列
图2 BWCQR估计下沪深股指标准化残差序列
3 结语
本文提出了GARCH模型的BWCQR估计并探究其大样本性质. 数值模拟结果显示: 当扰动项序列服从正态分布时, QML估计略优于BWCQR估计; 当扰动项序列服从厚尾分布时, BWCQR估计明显优于传统估计. 我们将提出的BWCQR拟合分析上证和沪深股指波动系统, 结果表明BWCQR估计能更为合理有效地刻画股指时序的波动规律.

