基于均值零化算子的灰色绝对关联度模型的改进及其应用①

罗丹， 王松华

百色学院 数学与统计学院， 广西 百色 533000

上世纪80年代邓聚龙教授提出灰色关联分析理论[1]， 随后这一理论得到了极大的发展与应用[2-15]． 后1991年文献[2]根据邓氏灰色关联分析模型[3]研究了一类广义灰色关联分析模型， 首次提出了绝对关联分析模型． 该模型有效解决了许多科研、 生产中的实际问题， 一直以来受到研究者的广泛关注． 在文献[2]提出的灰色绝对关联分析模型中， 灰色关联算子起到了重要的作用． 但考虑到绝对关联度分析模型在做实际问题的定量分析时， 存在因自然灾害、 战争、 疫情等意外因素的影响引起系统行为序列数据受到冲击干扰而失真的问题， 本文采用均值化算子构造方法提出一种均值化的新关联算子并对灰色绝对关联度模型进行改进， 并讨论该改进模型的性质和应用．

1 新的灰色关联算子的构造

定义2设系统行为序列Xi={xi(1)，xi(2)， …，xi(n)}，D为序列算子且

XiD={xi(1)d，xi(2)d， …，xi(n)d}

2 改进的灰色绝对关联度模型及其性质

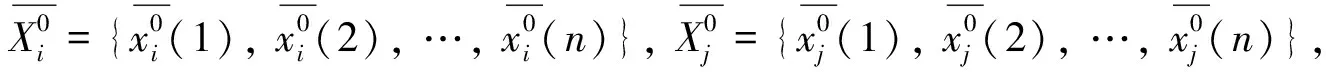
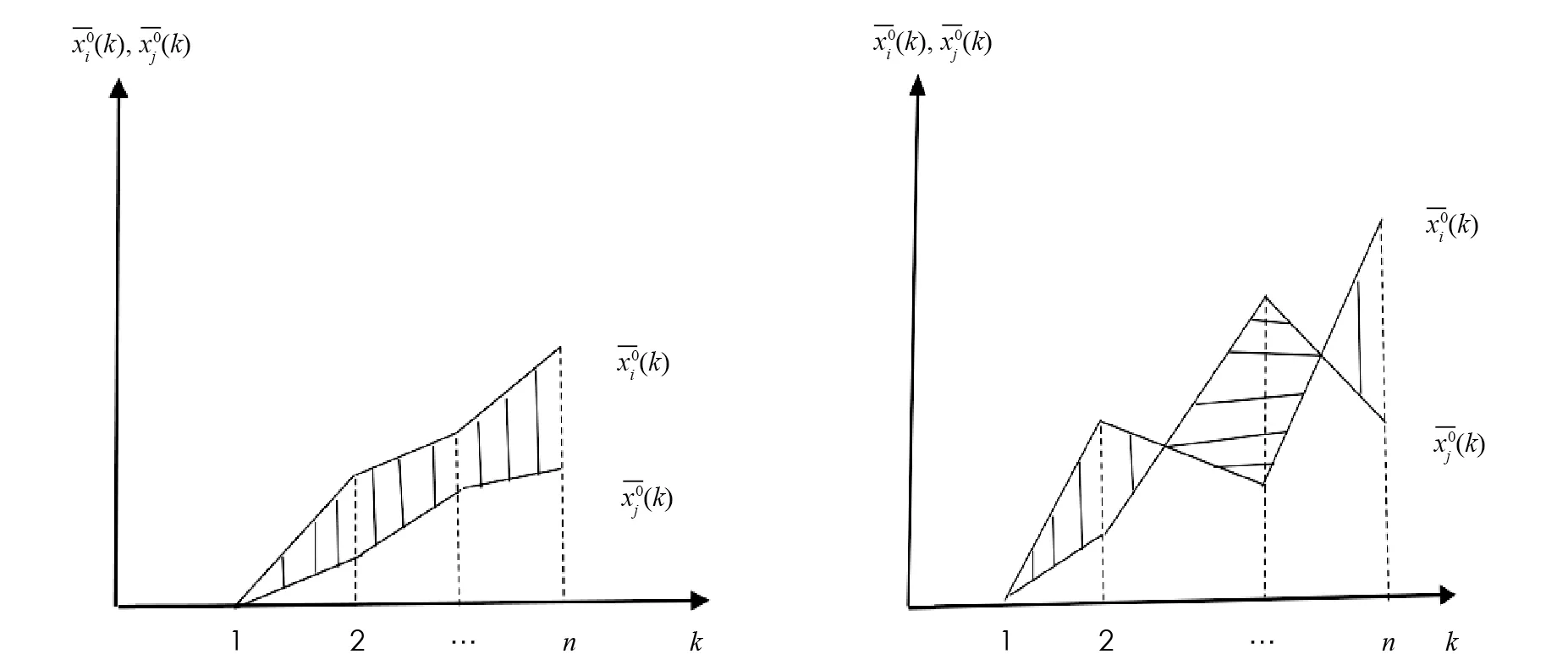
恒在的上方与相交

定理2广义灰色均值关联度

满足灰色关联公理中规范性、 偶对称性与接近性．

3) 接近性： 显然成立．

定理3设Xi与Xj的长度、 时距相同且皆为等时距序列， 则

证不妨设Xi与Xj皆为1时距序列， 由引理1和定义1得

3 实例分析

例1由文献[4]， 设有如下数据序列：

其中：X1为参考序列，X2与X3为相关因素序列． 计算得到的关联度及其关联序见表1， 数据序列折线图见图2．

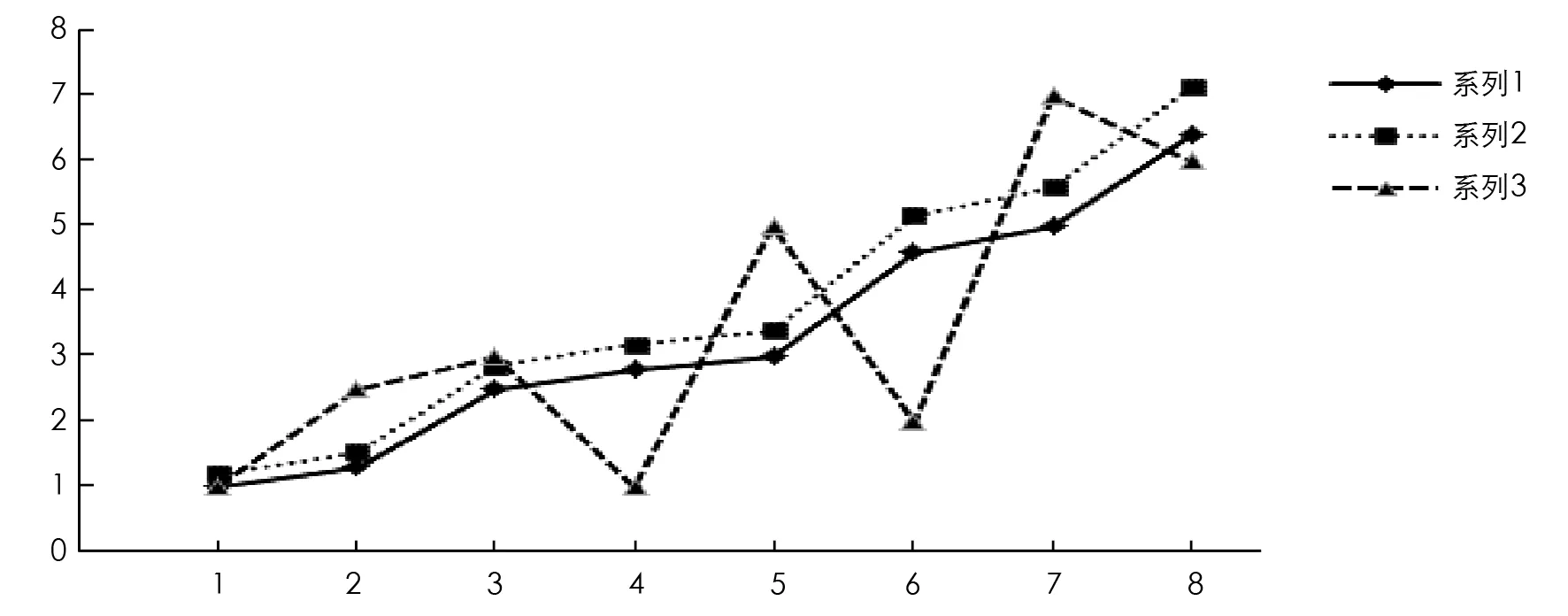
图2 例1数据序列折线图

表1 关联度与关联序

由图2可以看出， 序列X1和X2的发展趋势更接近， 而序列X1和X3的发展趋势差异较大， 即ε13<ε12． 所以， 本文构造的灰色关联度如实地反映了数据序列发展态势的相似程度．

例2引用文献[5]数据(表2)对我国海洋渔业经济增长与其影响因素的关系进行研究．

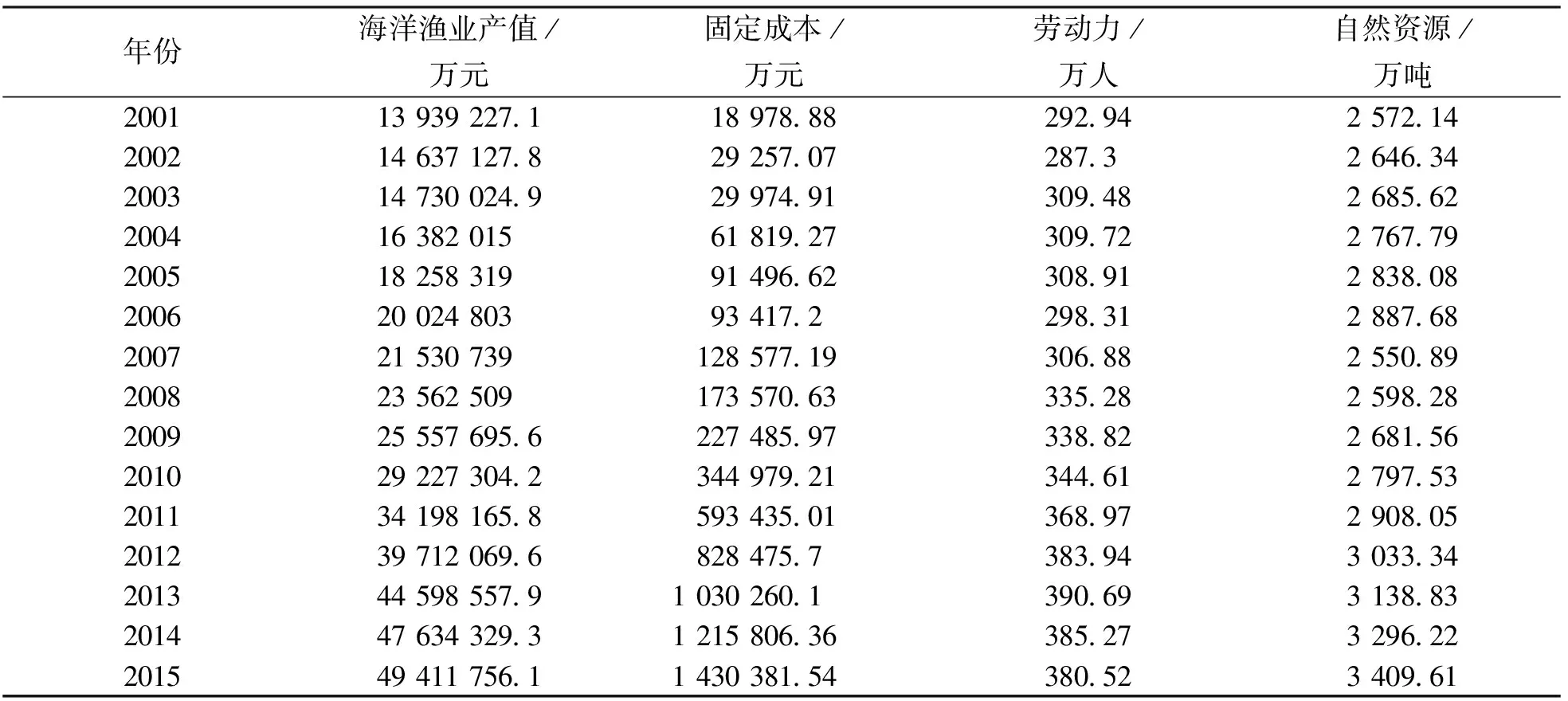
表2 2001-2015 年我国海洋渔业数据

将中国海洋渔业产值作为系统行为的参考序列X0(t)， 把固定成本、 劳动力、 自然资源看作X1(k)，X2(k)，X3(k)，k=2001，2007，…，2015.利用本文算子构造的灰色关联模型计算步骤及结果如下：

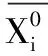
表3 均值零化像计算结果表

3) 由新构造的灰色均值关联度计算公式

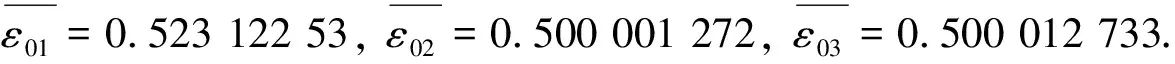
本文构造的新的灰色均值关联度模型计算结果跟实际情况相符合， 具有一定的实用性和可靠性．

4 结论

针对在利用灰色绝对关联度分析模型做实际问题的定量分析时， 存在因自然灾害、 战争、 疫情等意外因素的影响， 引起系统行为序列数据受到冲击干扰而失真的问题， 文章根据广义灰色绝对关联分析模型基本思想， 采用均值化算子构造方法， 提出一种名为均值零化的新关联算子并对灰色绝对关联度模型进行改进． 改进的灰色绝对关联度模型具有规范性、 偶对称性、 接近性等性质． 初步的数值实例表明， 改进的灰色关联度模型能真实地反映序列曲线的关联程度， 所得关联分析结果较为客观可靠， 新的灰色均值关联度模型算法简单且易于在计算机上实现， 具有一定的实用参考价值， 从而进一步拓宽了广义灰色关联度模型的应用领域．