不等厚钢板对接焊缝焊接残余应力研究

巨航瑞， 冯伟， 郭瑞鹏， 柳春风， 田晓阳， 张光桥， 赵建锋， 杨国涛

（1.青岛理工大学土木工程学院，山东 青岛 266033；2.山东高速工程建设集团有限公司，济南 250014；3.山东省路桥集团有限公司，济南 250014）

0 引言

在各式各样的钢结构工程中，焊接是最常用的连接方式之一，几乎遍及各种工业制造领域［1］。钢结构桥梁以其自重轻、施工简便、整体性好、跨度大等优点在实际工程中被大力推崇［2］。焊接与其他链接方式相比具有整体性好，强度高等优点，使得焊接在现代钢结构桥梁施工中占有举足轻重的地位。虽然焊接技术应用广泛，但其缺点也是显而易见的。高温加热结合金属的焊接技术，伴随着复杂的升温和冷却过程，会在钢结构内部产生残余应力，间接影响钢结构的服役寿命［3，4］。

近年来，随着计算机及数值模拟计算方法的成熟与发展，采用有限元模拟的方法更能直观高效地对焊接过程进行研究。马锋等［5］利用ABAQUS研究了各种线性单元类型对焊接模拟过程的计算精度及计算效率的影响，综合考虑有限元模拟的精度和效率认为减缩积分在保证计算精度的同时能提高计算效率。林升等［6］基于ABAQUS，通过对Q345B钢板对接焊缝进行三维模拟分析，研究了厚板表面纵向、横向残余应力分布规律，并发现对于厚度小于70mm的钢板，对接焊缝钢板表面纵向残余应力随着板厚的增加而增加。蔡建鹏［7］等以ABAQUS为平台，对16mm厚的Q345钢板对接接头进行了数值模拟研究，并与盲孔法测得的试验结果进行对比验证，研究结果表明纵向拉伸应力范围随焊缝层数的增加而减小。钱海盛等［8］通过盲孔法研究了工艺参数对Q235对接焊缝焊接残余应力大小的影响，结果表明保持焊接电流或电压任一参数不变，焊接残余应力都会随另一参数的增大而增大。李琴等［9］对Q345平板对接焊缝进行仿真模拟，研究了焊接速度和焊接层间温度对焊接残余应力的影响。现有的研究覆盖了焊接工艺的大部分参数，分析了不同焊接参数下对接钢板焊接残余应力的各种规律。虽然已有大量学者通过数值模拟或者试验的方法对钢板对接焊缝焊接残余应力分布及大小进行了研究，但对于不等厚钢板焊接残余应力的分布规律鲜有研究。随着我国钢结构桥梁发展，焊接始终是一项不可或缺的连接技术，在钢结构桥梁的设计过程中出于经济性的考虑，往往会出现不等厚钢板对接焊缝的情况，为了进一步提高钢结构桥梁的安全性和可靠性，开展不等厚钢板焊接残余应力研究是很有必要的。

文中基于ABAQUS有限元模拟软件，利用双椭球热源模型、生死单元技术等对Q345qD不等厚钢板对接焊缝进行了建模分析。同时利用盲孔法对试件进行残余应力测量，通过试验结果与计算结果的对比，探讨不等厚钢板对接焊缝残余应力的分布规律，为不等厚钢板焊接技术提供一定的参考作用。

1 试验材料及方法

1.1 试验材料及焊接工艺参数

实际两块待焊接母材为Q345qD钢板，尺寸分别为300mm×150mm×16mm和300mm×150mm×24mm，下表面对齐，将较厚钢板上表面切割出1：2.5的斜面向较薄钢板进行过渡，试件几何尺寸如图1所示。采用二氧化碳气体保护焊，开X型破口，上表面焊道分3层，角度为45°，下表面焊道分2层，角度为60°，每层焊道焊接工艺参数如表1所示，坡口形式及焊道顺序如图2所示。在焊缝两端设置引弧板和熄弧板，除此之外再无多余约束。

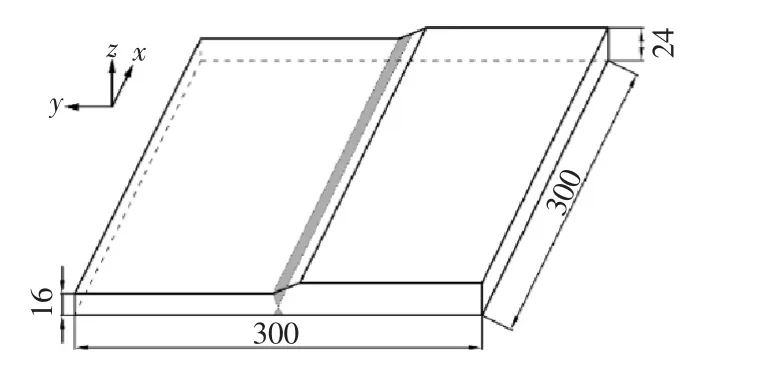
图1 试件几何尺寸（单位：mm）

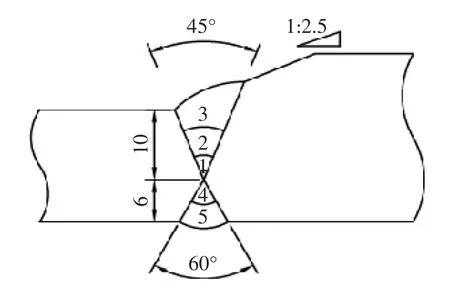
图2 破口形式及焊道顺序（单位：mm）

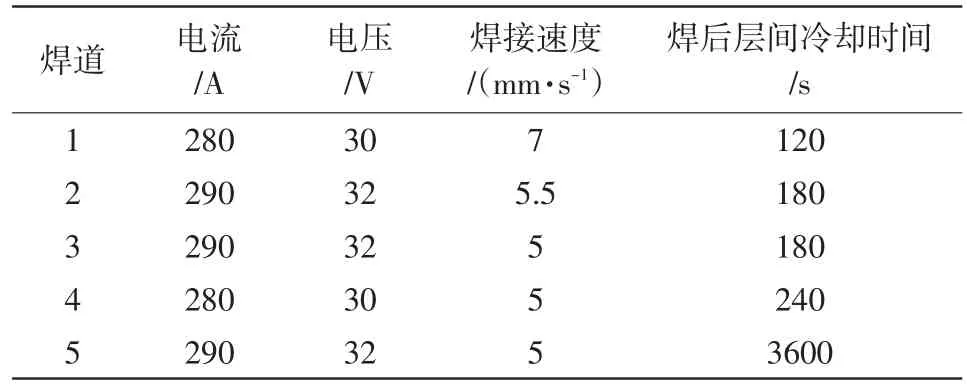
表1 每层焊道焊接工艺参数

1.2 盲孔法残余应力测试

盲孔法因其简单易行，测量精度高而在焊接残余应力测量中广泛应用。试验采用盲孔法专用钻孔仪，通过型号BX120-2CA应变花及静态应变采集仪进行应变数据采集。由于试验研究的是不等厚钢板焊接的残余应力不能取一半试件进行测量。在试件上表面设置Path-1和Path-2两条路径，Path-1过焊缝中点且垂直于焊缝方向，Path-2平行于焊缝方向且距焊缝中心线30mm。Path-1路径上布置十个测点，分别标记序号1～10，Path-2路径上布置十个测点分别标记序号11～20（Path-1与Path-2交叉点只做一次标记），测点布置如图3所示。使用砂纸轮和砂纸将试件测点周围表面打磨光滑，然后用丙酮擦拭干净，待丙酮挥发后粘贴应变花，将应变花与应变采集仪连接后安装钻孔设备，钻取直径1.0mm，深度1.5mm的盲孔并读取应变值。

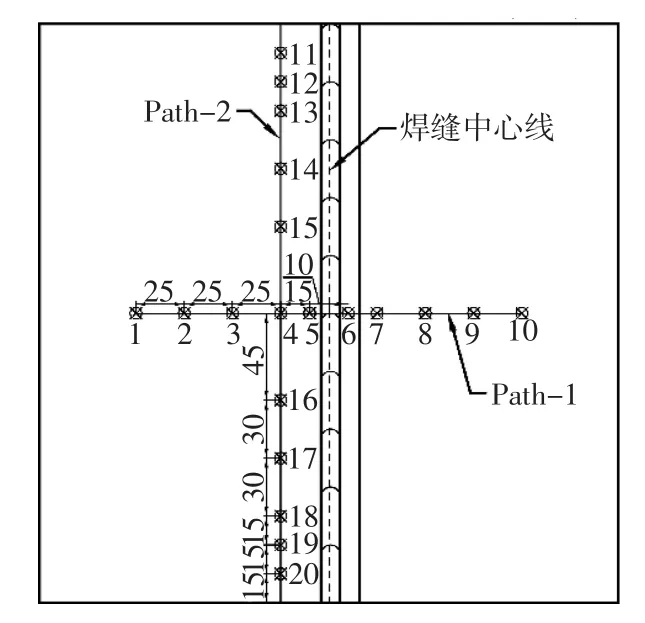
图3 测点布置（单位：mm）

由于试验只研究平行于焊缝方向的纵向残余应力和垂直于焊缝方向的横向残余应力，只需将0°和90°应变片分别平行和垂直于焊缝方向粘贴，测得平行及垂直于焊缝两方向的应力即可计算两条路径的纵向及横向残余应力，其计算公式为：

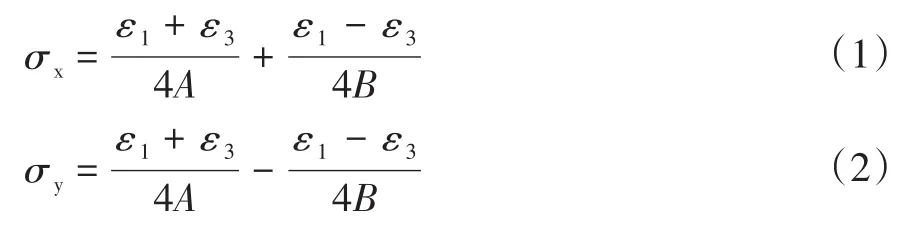
式中，ε1、ε2为x、y方向上的应变；σx、σy分别为x、y方能向上的应力；A、B为应变释放系数，由标定试验确定。

1.3 应变释放系数标定与修正

盲孔法测量焊接残余应力时，由于焊缝及焊缝附残余应力数值过大，其数值往往接近甚至超过材料的屈服强度，而盲孔法测量的计算公式是在弹性条件下推导出来的，因此为了在测量高残余应力时得到准确的结果，需要对应变释放系数A、B进行修正。依据GB/T 31310-2014《金属材料残余应力测定钻孔应变法》［10］，对退火后的标定试件进行单轴拉伸（σ1=σ3，σ2=0），将试验中应变片试验结果代入公式3，求出释放系数A、B。

式中，ε1、ε2分别为拉伸方向应变片的应变值和垂直拉伸方向应变片的应变值；σ3为拉伸应力。

应变释放系数A、B 与拉伸应力的关系如图4所示，可以看出当应力小于1/3σs时，随着应力的增大，A和B的值保持不变，而当应力大于1/3σs时，A和B的值随着应力的增大而增大。引入形状改变比能参量S，并对应变释放系数进行修正。应力释放系数A、B与S的关系如图5所示，并对曲线进行拟合，得到修正后的公式：

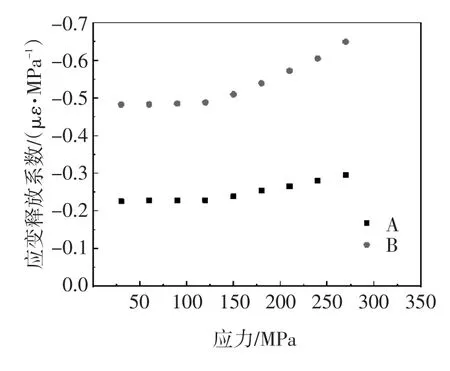
图4 应变释放系数与应力的关系

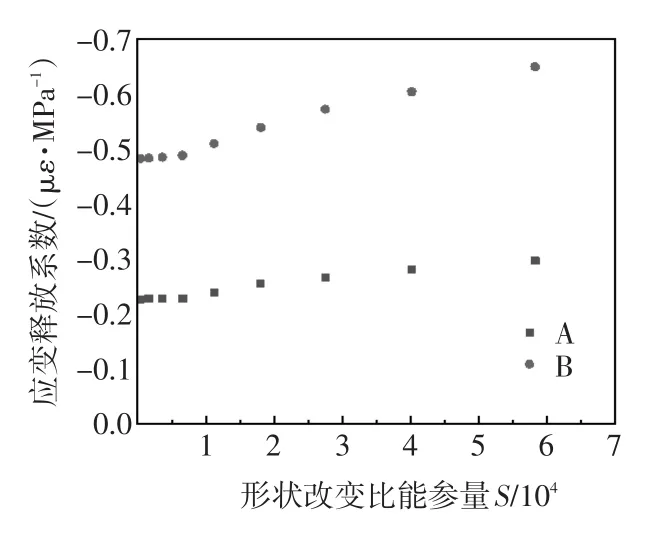
图5 应变释放系数与相撞改变比能参量S的关系

2 有限元模型计算

2.1 几何模型建立

文中基于有限元软件ABAQUS建立了与实际焊接试件尺寸相同的300mm×300mm×16mm（24mm）有限元模型，为了在保证计算精度的同时兼顾计算速度，应对不同区域采用不同的网格划分方法。由于焊缝热影响区附近温度变化梯度较大，对靠近焊缝附近区域的网格需要细致划分，远离热影响区的边界温度变化梯度较小，故对远离焊缝的区域进行适当粗略划分，二者之间采用过渡网格过渡。试件在焊接过程中未施加外部约束，故对有限元模型仅施加防止模型发生刚体位移的边界条件，边界设置及网格划分如图6所示，在点A约束x、y、z三方向的线位移，在B点约束x和z方向的线位移，在C点约束z方向的线位移。采用单项耦合的方法进行模拟计算，首先求解温度场，然后在求解应力场的时候将计算出的温度场结果作为外荷载施加在模型上进行应力场的求解。温度场求解采用六面体DC3D8单元求解，应力场采用六面体C3D8R单元进行求解。采用“生死单元”技术来模拟焊缝的填充，即利用ABAQUS中的“model change”功能实现各层焊道的“激活”与“钝化”。环境温度设置为20℃，并同时考虑试件表面与环境之间的热对流和热辐射，对流换热系数设置为15W/（m2·℃），热辐射系数设置为0.85。

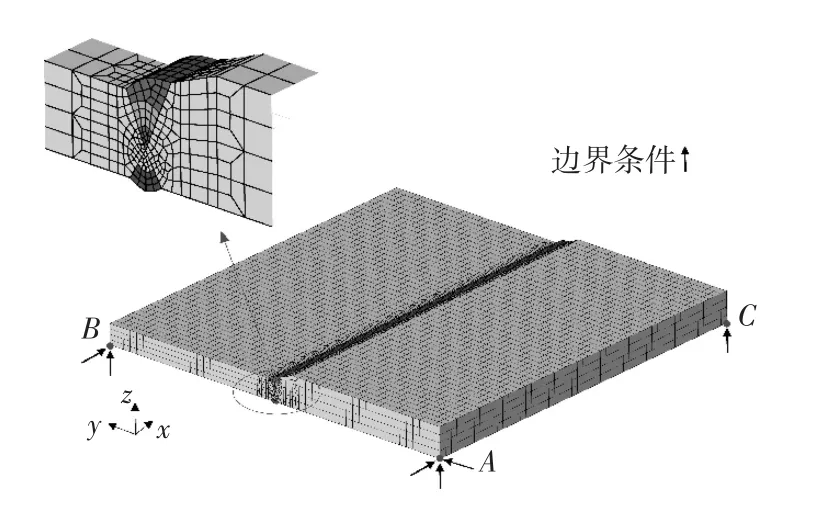
图6 边界条件及网格划分

2.2 材料性能参数

焊接材料的物理参数及力学性能具有较强的温度相关性，为了得到准确温度场与应力场，必须考虑材料不同温度下的热物理及热力学参数，根据文献［11］获得Q345qD钢板在不同温度下的热物理性能参数（密度，热导率、比热容）如图7所示，力学性能参数（弹性模量、泊松比、屈服强度、热膨胀系数）如图8所示。假设焊缝填充金属与母材具有相同的热物理性能及力学性能。

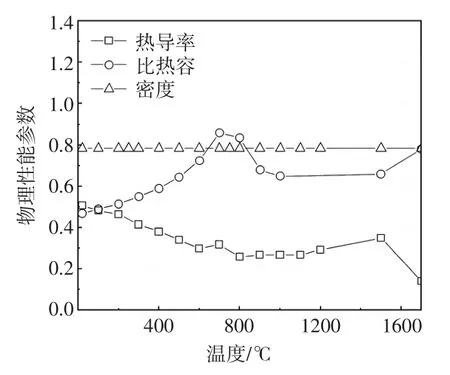
图7 物理性能参数

图8 力学性能参数

2.3 焊接热源模型

焊接热源是焊接过程的能量来源，焊接热源的选取决定焊接温度场及应力场模拟的准确性。试验采用二氧化碳气体保护焊的焊接方式，选用双椭球移动热源较为合适。双椭球移动热源由Goldak［12］提出，几何形状类似半卵形，在焊接方向由前后2个1/2椭球组成，模拟了电弧前进时，电弧前方加热区域比电弧后方小的特点，比较好地反映了热源前进过程中的热流分布情况，如图9所示。前、后半椭球的热源数学表达式为：

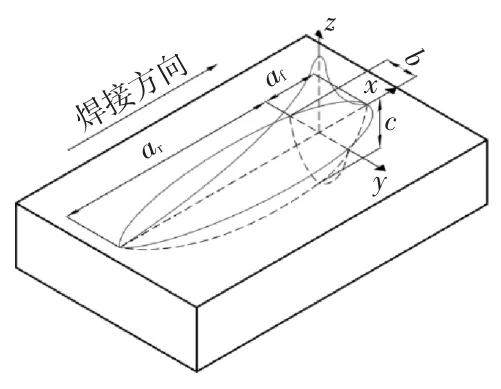
图9 双椭球热源模型

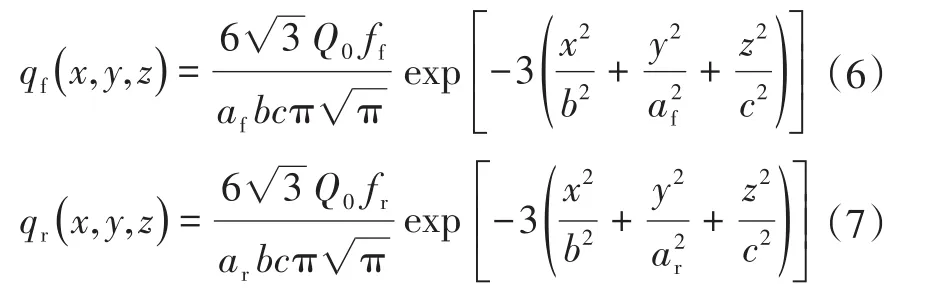
式中，qf、qr分别为前后半椭球热源模型的焊接热流密度；Q0为焊接热输入，Q0=ηUI，η为热效率，U为电压，I为电流；af、ar分别为焊接熔池前后长度参数，b为熔宽，c为熔深；ff、fr分别为前后半椭球的热流密度分布系数，且ff+fr=2。

3 模拟结果与试验验证

3.1 焊接温度场模拟结果

焊接温度场的计算精度直接影响到应力结果的精确性，在每层焊缝的焊接过程中，热源加载在每层焊缝单元上，每层焊缝有加热至钢材熔点和冷却至层间温度两个过程，文中模型一共有5层焊缝，完成最终焊接后冷却至室温，焊接时的温度场云图如图10所示。随着热源的移动，焊接过程达到稳弧，前半部分椭圆温度梯度大，且随着时间延长沿焊缝方向长度及作用面积变化不大，后半部分温度梯度较小，且随着时间的延长，后半部分椭球热源沿焊缝方向的长度增大，覆盖面积更广。第五道焊缝峰值温度最高，第三道焊缝峰值温度最低，各层焊缝的峰值温度介于2385.8～3118.4℃之间，这是因为每层焊缝的热输入、热对流及热辐射条件不同，但是都会经过一定的层间冷却时间，使层间温度冷却至100～200℃，然后进行下一层的焊接。文中试验材料的熔点大约为1500℃，温度高于1500℃的部分定义为焊缝的熔池。为确定熔池形貌，在试件焊缝位置截取出包含焊缝接头断面的小多面体试件，并对其进行酸蚀试验观察熔池形状，确定熔合线位置。如图11所示，将酸蚀试验所得焊缝熔池形状与模拟所得熔池形状进行对比，可见模拟结果与试验结果吻合较好，模拟热源与实际热源相符。

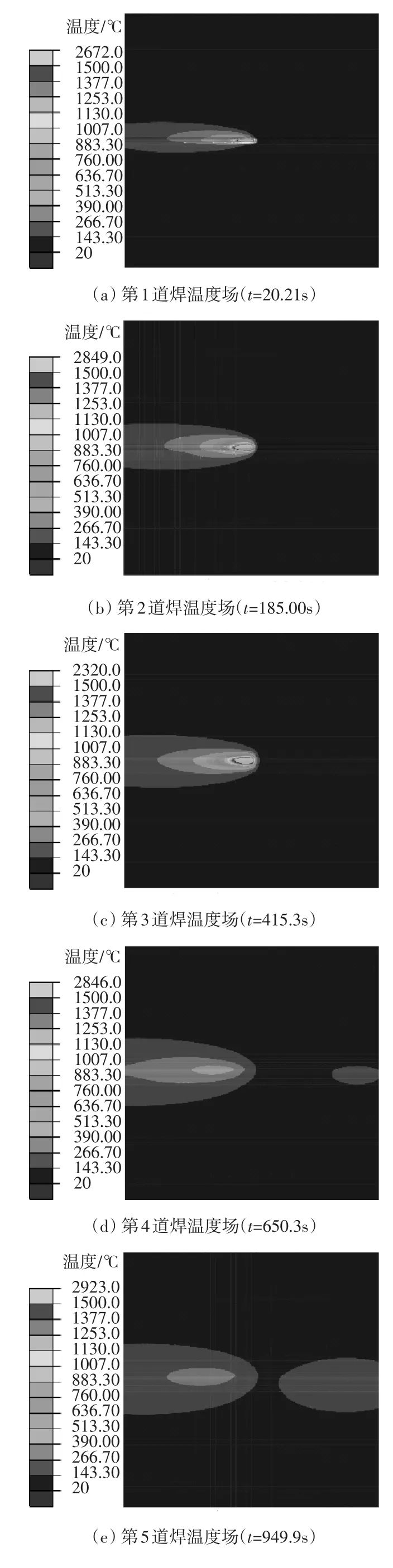
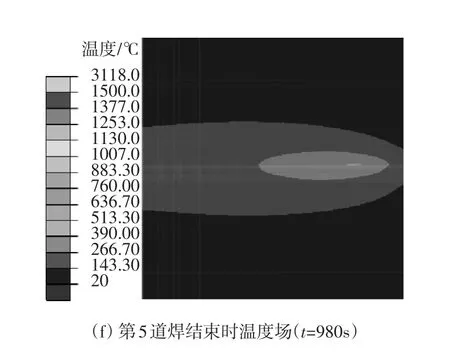
图10 焊接温度场

图11 第三层焊缝熔池形状对比

3.2 焊接残余应力场

图12为不等厚钢板焊接残余应力场云图，可以看出焊接残余应力在两块不同厚度钢板上的分布并不对称。纵向残余应力是平行于焊缝方向的，横向残余应力是垂直于焊缝方向的。纵向残余应力在焊缝中部主要表现为拉应力，且拉应力峰值接近材料的屈服强度，在焊缝的两端拉应力逐渐减小，且在焊缝端部出现小部分压应力。纵向残余应力在远离焊缝区域主要表现为压应力，且在较薄板一侧的压应力峰值大于较厚板一侧。横向残余应力在焊缝及两侧的热影响区均表现为拉应力，热影响区的拉应力普遍大于焊缝处的拉应力。在焊缝起弧、息弧的端部位置。横向残余应力表现为较大的压应力，且向焊缝中段逐步过渡为拉应力。

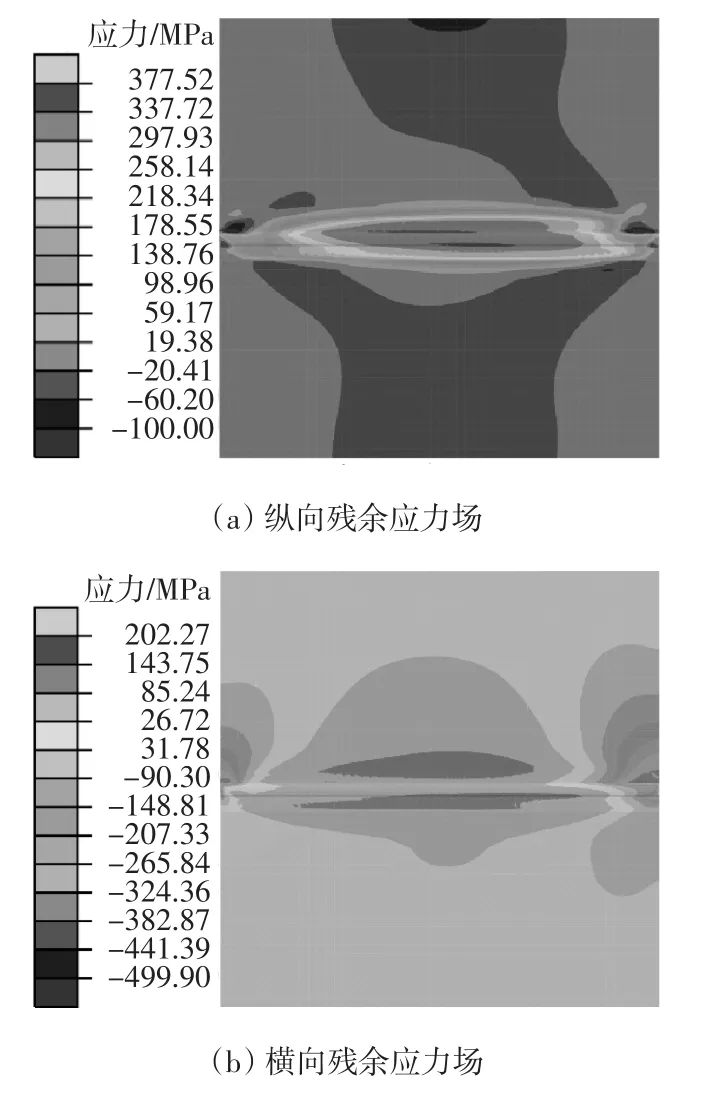
图12 残余应力场

在计算模型上表面分别选取与试验中位置相同的两条路径，将两条路径上的残余应力结果于试验结果进行对比，如图13所示，可以看出数值模拟结果与试验测得的焊接残余应力分布趋势基本一致，焊接残余应力的数值大体吻合。由图13（a）可知，Path-1路径上的纵向残余应力沿路径呈压-拉-压分布趋势，拉应力峰值出现在焊缝区域，达到340.5MPa，随着离焊缝距离的增大纵向残余应力迅速转变压应力，其大小与实测值基本吻合，在远离焊缝的边缘位置，较薄板一侧的纵向残余应力水平略大于较厚板一侧，这是由于两侧破口尺寸及板厚不同而在同一热源的作用下，较薄一侧单位体积的热输入较大导致的。由图13（b）可知Path-1路径上数值模拟的横向残余应力分布趋势与试验结果大体吻合，在焊缝及热影响区表现为拉应力，且在焊缝中心位置向两侧热影响区过渡时，拉应力出现了明显的激增，焊缝中心拉应力数值为41.8MPa，较薄一侧热影响区的拉应力峰值为114.3MPa略大于较厚钢板一侧，数值模拟结果与试验测得结果在数值大小上存在差异的主要原因可能是盲孔法试验的误差或数值模拟材料参数与实际焊接过程有所差异。当Path-1路径上横向残余应力由热影响区向试件边缘过渡时，其拉应力大小逐渐减小，且在两侧钢板上的分布趋势并不对称，在较薄钢板一侧，其拉应力大小变化较缓，而在较厚钢板一侧，拉应力的大小呈现先陡后缓的变化趋势。

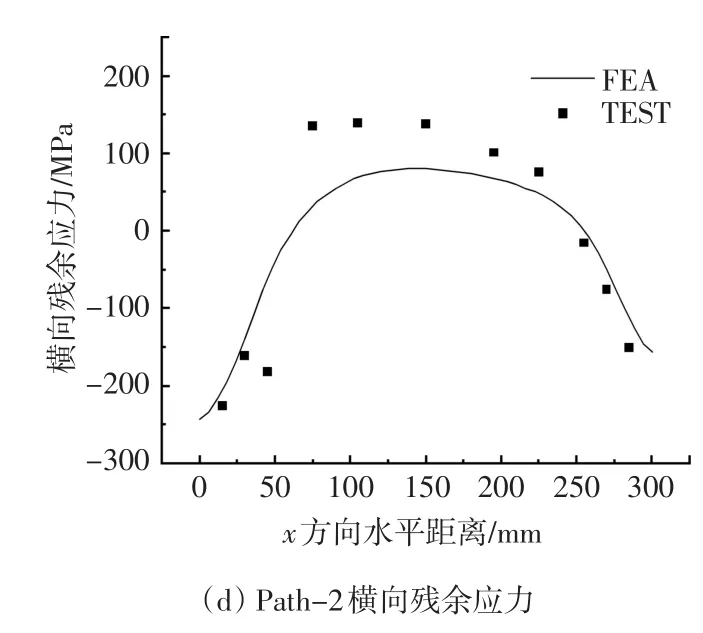
图13 数值模拟与试验结果对比

由图13（c）可知，Path-2路径上的纵向残余应力在试件边缘表现为极低的应力水平，由两侧向试件中心过渡时，纵向残余应力表现为压应力，且左右变化趋势较对称，在距离试件边缘50mm左右的区域出现压应力峰值，而在试件中心位置纵向残余应力又表现为较小的拉应力。由图13（d）可知，Path-2路径上的横向残余应力在试件边缘表现为较大的压应力，向试件中心逐步过渡为拉应力，且在边缘两侧50mm范围内应力变化显著，中间200mm范围内应力变化平缓。

4 结语

文中基于ABAQUS对不等厚钢板对接焊缝残余应力数值模拟，并将数值模拟结果与盲孔法试验测得的结果进行验证，得出以下结论：

（1）纵向残余应力在垂直于焊缝的路径上呈现出压-拉-压的分布规律，焊缝附近及热影响区表现为拉应力，其最大拉应力出现在焊缝附近，接近材料的屈服强度，在较薄钢板边缘一侧的压应力数值略大于较厚钢板一侧，不等厚钢板对接焊缝残余应力在平行焊缝方向分布与等厚钢板残余应力分布规律几乎相同。

（2）横向残余应力在垂直于焊缝方向表现为拉应力，且分布规律存在明显的不对称性，在较薄钢板一侧的残余应力大于较厚钢板一侧的残余应力，在平行焊缝路径上的焊缝两端位置表现为较大的压应力，边缘50mm范围内压应力变化显著，中部应力表现为拉应力且变化平缓。

（3）在实际钢桥设计过程中不仅要着重考虑纵向残余应力峰值过大的问题，也要考虑残余应力在垂直焊缝路径上分布的不对称性。