ECC低干预加固结构数值模拟研究

方先慧，邓嘉瑞，张军朋，李晓琴

(昆明理工大学 建筑工程学院，云南 昆明 650500)

穿斗式木结构广泛应用于南方地区的民居建筑中，特别是在西南地区应用较多，也是云南主要的村镇民居建筑形式[1-2].穿斗式木构架本身起主要承重作用，以贯穿柱截面的穿枋将柱联结成一排木架，木檩直接支撑于柱头而不设置梁[3].木构架通常以砖墙或土墙作为围护结构.云南省为我国经济欠发达地区，由于经济上的原因农村民居多为自建房，房屋建造主要凭经验，缺乏正规的设计与施工[4]，大部分不满足《建筑抗震设计规范》[5]设计要求，存在安全隐患.木构架与砌体围护墙由于质量、刚度、自振特性的不同，在地震作用下产生的位移不一致，会导致墙体-木构架碰撞开裂，因此《建筑抗震设计规范》[5]规定木构架与墙体之间应设置水平拉结筋或拉结网片，同时也规定木结构房屋不应采用混合承重，不得采用硬山搁檩.然而现有的穿斗式木构架民居即使承重结构设计合理，大部分仍存在构造方法不当的问题，存在地震作用下维护结构开裂倒塌的风险[6]，因此，对维护结构的加固十分必要.

针对现有结构的加固方法主要有钢材加固方法(外贴钢板加固和水平嵌筋加固)[8]、钢筋混凝土加固[9](钢筋混凝土加固[10]、砂浆带加固[10])、ECC加固[11]和注浆(环氧树脂)加固[12]等方法.其中，注浆加固造价过高，约为4万元/t，经济性较差，且研究[12]表明砌体结构注浆加固耗能能力仅提升1倍；钢材加固方法造价约为0.6万元/t，但其加固材料涉及的碳排放因子最高，在2 000 kg CO2e/t以上；尽管钢筋混凝土加固方法加固效果最好且造价最低约为0.1万元/t，但所涉及的材料碳排放因子和用量仍然较高(其中混凝土碳排放因子295 kg CO2e/m3)；而尽管ECC加固造价约为0.3万元/t，但加固材料用量较混凝土加固用量少，且研究[11]表明砌体结构ECC加固耗能能力能提升3倍，加固效果较好.且ECC原材料大量采用工业废料粉煤灰代替水泥[13]，相对于传统混凝土材料碳排放急剧减少，高粉煤灰掺量ECC其碳排放因子仅约为100 kg CO2e/t，符合节能减排的要求.此外，钢或钢筋混凝土加固等方法的施工工艺都较为复杂，部分加固办法需在原有建筑结构表面进行钢筋锚固等操作会影响原有结构.而ECC加固施工工艺简单，只需在加固构件、结构内、外侧通过喷射或抹面实现一薄层ECC敷面加固即可，基本不影响原构件截面，是一种简单易操作的低干预加固方法.

由于现有的针对穿斗式木构架的试验、模拟研究主要针对木节点[14-18]、木构架承重主体[19-23]拟静力抗震或振动台试验研究，鲜有研究针对带填充墙的穿斗式木构架的拟静力试验/模拟研究，而研究表明[24]：对砖填充墙榫卯节点木框架进行抗震鉴定和加固时,应考虑砖填充墙的影响，故选取带填充墙的穿斗式木构架进行加固模拟研究.

针对填充墙与木构架间没有搭接措施的云南民居应该采取拉结筋与ECC共同加固的方法，这也是作者正在进行的研究，但本文旨在先分析讨论单纯的ECC加固维护结构对此种结构的贡献，即研究在不考虑填充墙与木构架之间拉结而仅考虑木构架本身对维护结构产生的约束效应的情况下研究ECC单面加固木构架填充墙的面内与面外抗震性能.首先，基于ABAQUS[25]大型非线性有限元软件并选取具有一定相似性的单层单跨的带填充墙木框架试件[8]与木楼盖砌体墙试件平面内外加载，验证有限元模型的可靠性；随后，基于云南“一颗印”做法[26]设计一榀带填充墙的穿斗式木构架数值模型进行平面内拟静力循环加载与平面外推覆加载；再引入ECC材料对填充墙单面加固，评价平面内外的加固效果，表明此加固方法对填充墙平面外承载能力有明显的提升.基于此，进行不同损伤填充墙平面外抗倒塌加固有限元模拟，评价不同损伤状态下ECC单面加固的效果，给与工程加固以科学的指导方法.

1 带填充墙的穿斗式木构架数值模型

1.1 有限元模型

本研究拟采用三维建模方法来建立带填充墙的穿斗式木构架民居模型.木构架与填充墙均采用C3D8R单元进行建模，木构架榫卯连接处采用面面接触，定义其法向“硬”接触以及切向“罚”刚度来模拟接触的摩擦行为[18]，对于通榫式木节点木材之间摩擦系数取值在0.3～0.38之间，其具体数值根据对比试验与模拟的滞回曲线、骨架曲线确定，最后确定摩擦系数为0.38.为防止模型穿透对结果产生影响，从面网格尺寸应小于主面.木构架与填充墙之间的接触同样采用以上方法，摩擦系数根据《砌体结构设计规范》[27]取0.6.填充墙目前建模的方法有三种，分别为整体式模型、简化微观模型与精细化微观模型，如图1所示.孔璟常[28]对比了一榀带填充墙RC框架采用整体式模型与简化微观模型两种建模方法，表明两种有限元模拟方法都能较成功地得到结构的初始刚度及承载力，整体式模型软化段模拟结果稍逊于简化微观模型，但简化微观模型考虑了组合砖之间的界面模拟，导致计算成本远高于整体式建模方法.考虑到模型大小与计算成本，填充墙采用整体式建模方法建模.

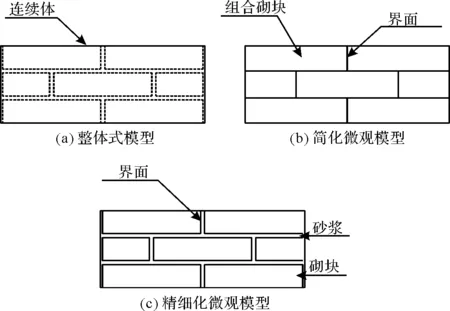
图1 填充墙模型Fig.1 Infilled wall models

1.2 材料模型

1.2.1 砌体墙材料模型

均质化后的填充墙采用ABAQUS中的塑性损伤模型(Concrete Damaged plasticity Model，CDPM)进行模拟，该模型假设材料的破坏方式为受拉开裂和受压压溃，适用于材料在单调荷载、循环荷载及动态荷载作用下的数值分析.砌块与砂浆组合成的砌体材料属于脆性材料，难以得出其受拉应力-应变曲线的下降段，故定义砌体抗拉强度达到抗压峰值荷载的1/10即认定材料破坏.采用应力-非弹性应变曲线来模拟砌体的受压行为，砌体的受压应力-应变曲线按照杨卫忠[29]提出的本构计算.

(1)

(2)

(3)

(4)

式(1)～(4)中：σ、fm分别为砌体受压应力值、抗压强度平均值；ε、εm分别为砌体受压应变值、峰值应变值；η为砌体弹性模量与峰值变形模量之比，取 1.633[30]；d为砌块的受压损伤因子.fm为均质后的抗压强度，其中：f1、f2分别为砌块和砂浆的抗压强度.

由于本次带填充墙木框架进行的是循环往复加载，受拉刚度恢复因子取默认值进行数值计算，即wt=0，受压刚度恢复因子wc经大量试算后取为0.6.塑性损伤模型中塑性参数取值见表1.

表1 塑性损伤模型中塑性参数取值Tab.1 Values of plastic parameters of CDPM

1.2.2 木材材料模型

木材本构采用受拉弹性，受压弹塑性进行模拟[31].其中弹性只用定义9个工程常数，分别为纵纹(L)、横纹径向(R)、横纹弦向(T)的弹性模量、泊松比与剪切模量.塑性定义受压塑性，采用Hill屈服准则，以及abaqus里自带的potential函数模拟正交异性材料的屈服，定义6个常数，如式(5)所示.

R11=X/σ0,R22=Y/σ0,R33=Z/σ0,
R12=S12/τ0,R13=S13/τ0,R23=S23/τ0

(5)

1.3 模型验证

1.3.1 平面内拟静力加载模型验证

选取带填充墙的木框架拟静力试验试件KJ-1[8]，其节点连接形式为燕尾榫，与云南穿斗式木构架的台阶透榫连接同为榫卯连接的方式，试件详细尺寸如图2所示.试验砖与砂浆的实测抗压强度分别为19.03 MPa、3.18 MPa，木材顺纹抗压强度、顺纹抗压弹性模量、横纹抗压强度、横纹抗压弹性模量分别为32.4 MPa、14 050 MPa、9.5 MPa、6 640 MPa.将以上数据代入公式(3)与(4)中可得到砌体平均抗压强度为4.16 MPa，弹性模量为3 140 MPa，与文献[8]中一致.

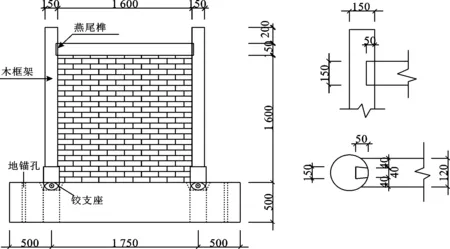
图2 带填充墙的木框架拟静力试验试件KJ-1试件设计图Fig.2 Design drawing of kJ-1 specimen for pseudo-static test specimen wood frame with infilled wall

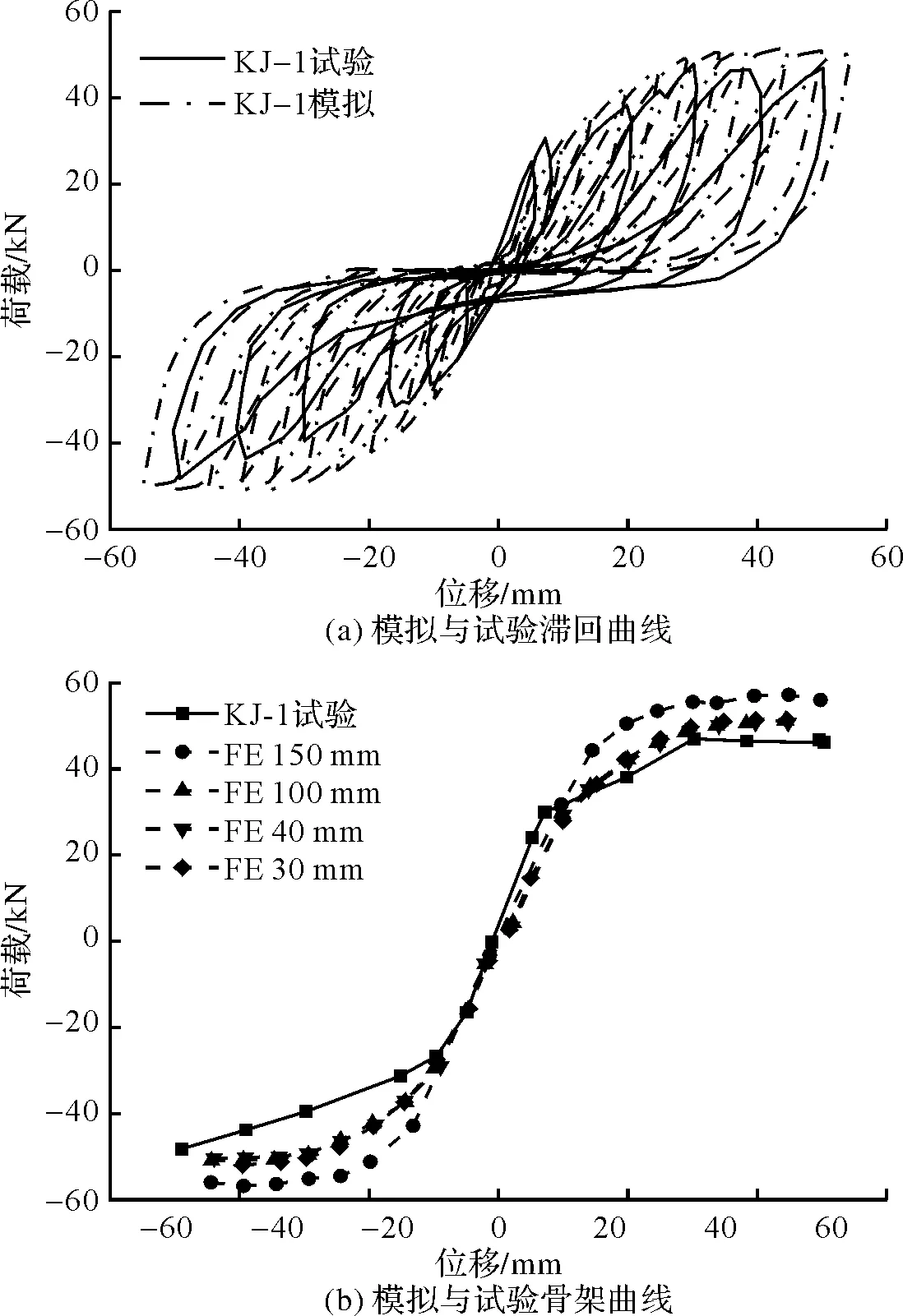
图3 试件KJ-1试验和模拟结果比较Fig.3 Comparison of test and simulation results of KJ-1 specimen

由图3(a)可知，模拟得出的滞回曲线形状与试验基本保持一致，由图3(b)可知150 mm、100 mm、40 mm、30 mm网格下的带填充墙木构架的正向骨架曲线较为接近，其对应的峰值荷载分别为57.2，51.4，51.2和50.7 kN，40 mm与30 mm网格下的正向峰值承载力与试验结果47.8 kN分别相差7.1%和6.1%，表明带填充墙的木构架在不同网格下的模拟结果已经收敛.试验测得的负向滞回曲线由作动器位移读取，而负向(即往回拉)的时候由于柔性牵引绳有伸长或端板滑移误差，会导致试验读取的负向滞回曲线和骨架曲线与正向相应曲线的不对称性，而数值模拟没有这个特征.因此，负向模拟骨架曲线结果与试验结果相差较大，这是边界条件设置缺陷导致的误差，在穿斗式木构架试验和模拟研究对照中普遍存在[8, 24, 32-33].

1.3.2 平面外静力加载模型验证

目前尚未见有关带填充墙的穿斗式木构架平面外加载试验文献的相关报导，因此选用具有一定相似性的文献[34]的W1试验数据进行平面外静力加载验证.试件W1为木楼盖砌体结构，受力砖墙厚度为240 mm，宽4 500 mm，高3 000 mm，受力砖墙两端设有宽760 mm，高3 000 mm，厚240 mm的正交横墙，正交横墙端部设置240 mm×240 mm混凝土柱，柱与横墙沿高度每隔300 mm布置拉结筋，保证受力砖墙平面外的约束力，具体如图4所示.试验采用MU10普通烧结砖与M2.5混合砂浆，实测抗压强度分别为29.3 MPa、2.69 MPa.采用C30混凝土，实测立方体平均抗压强度为38.4 MPa.拉结筋、构造柱箍筋实测屈服强度406 MPa，构造柱纵向钢筋实测屈服强度412 MPa.

试验中设置混凝土构造柱与砌体墙之间的拉结筋是为了保证受力砖墙平面外的约束力，为简化模型，不建立构造柱与砌体墙之间的拉结筋而将构造柱与混凝土之间设为绑定约束，即忽略了两个面之间的相对位移形成足够的面外约束力.将上述试验数据带入公式(3)与(4)得出均质化后的砌体平均抗压强度与弹性模量分别为5.02 MPa、4 162 MPa，平均抗拉强度根据《砌体结构设计规范》[27]表3.2.2取值0.09 MPa.

图4 砌体墙试件W1尺寸Fig.4 W1 size of masonry wall specimen

试件W1的有限元模拟结果如图5所示.由图可知模拟所得的曲线初始刚度都大于试验曲线，这是因为试验中拉结筋与砌体之间存在粘结滑移，而有限元模型中采用的绑定接触，忽略了由于钢筋与砌体之间的粘结滑移带来的两个面的相对位移，从而导致刚度模拟值大于实验值.随着网格尺寸缩小，平面外峰值承载力有递增的趋势，变化幅度明显，具有明显的网格依赖性.100 mm、50 mm、40 mm网格下的W1试件平面外峰值承载力分别为61.8 kN、74.3 kN、79.5kN，与试验值80.1 kN分别相差22.8%、7.3%、0.8%.表明墙体的平面外推覆模拟结果在40 mm网格下达到收敛，此结论与文献[35]一致.

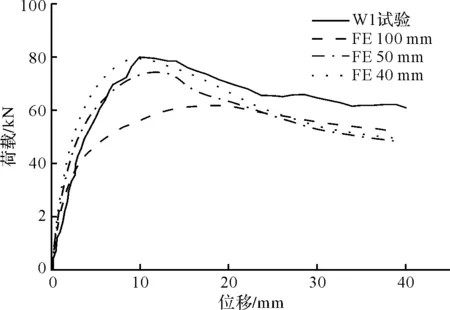
图5 砌体墙平面外荷载-位移曲线比较Fig.5 Comparison of out-of-plane load-displacement curves of masonry wall

综上所述，墙体平面内的拟静力加载与平面外的静力推覆加载有限元模拟在采用40 mm网格条件下能取得良好的结果，误差均控制在8%以内，验证了有限元模型的可靠性.

2 带填充墙穿斗式木构架数值模拟研究

基于滇南“一颗印”穿斗式木构架设计方法，云南传统穿斗式木构架民居一榀带填充墙框架的足尺模型[1]如图6所示.

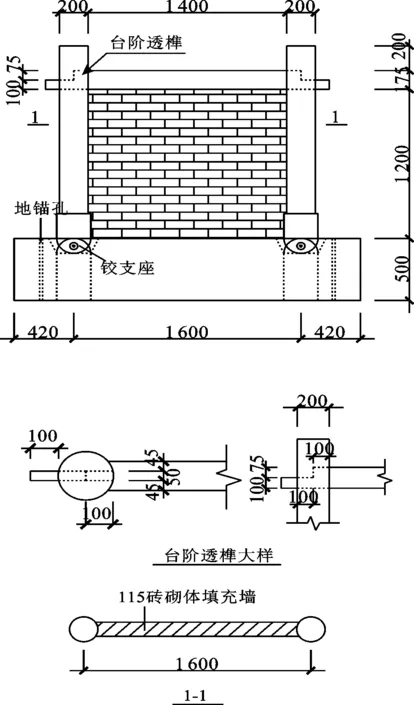
图6 一榀带填充墙框架的足尺模型Fig.6 A full scale model with infilled wall frame

与前述带填充墙木构架模型的节点形式不同，采用台阶透榫节点.木材采用杉木，材料参数如表2所示,砌块采用MU25烧结普通转，砂浆采用M2.5等级砂浆,根据公式(3)与(4)计算得到均质化后的砌体平均抗压强度fm与弹性模量E分别为4.58 MPa与3 627 MPa.为反映云南农村地区民居填充墙普遍未设置拉结筋，仅将填充墙与框架顶紧的现状，框架与填充墙采用罚摩擦接触模拟.砌块沿木材相对滑动的摩擦系数取0.6[27].

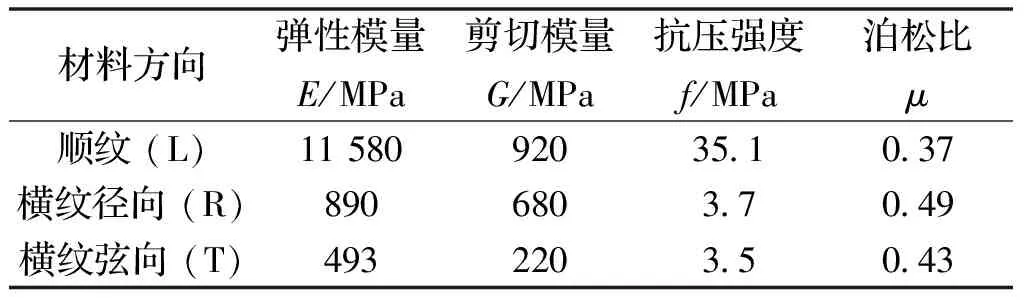
表2 杉木物理力学性能参数Tab.2 Physical and mechanical properties of Chinese fir

2.1 平面内拟静力加载模拟

平面内加载方式根据《建筑抗震试验方法规程》[36]在柱端采用荷载-位移控制加载方法，首先通过荷载控制，每级循环一次，记录墙体出现裂缝时的位移并记为Δ，后采取位移控制并以Δ为增量，每级循环两次直至填充墙破坏.

以0.1%应变作为砌体的极限拉伸应变，以40 mm特征长度的单元通过公式(6)计算砌体的Ⅰ型断裂能，得出损伤因子-断裂能曲线如图7(d)所示.当损伤因子为0.85左右砌体已消耗80%的断裂能，可以认为裂缝已经产生，因此损伤因子大于0.85的区域视为破坏.

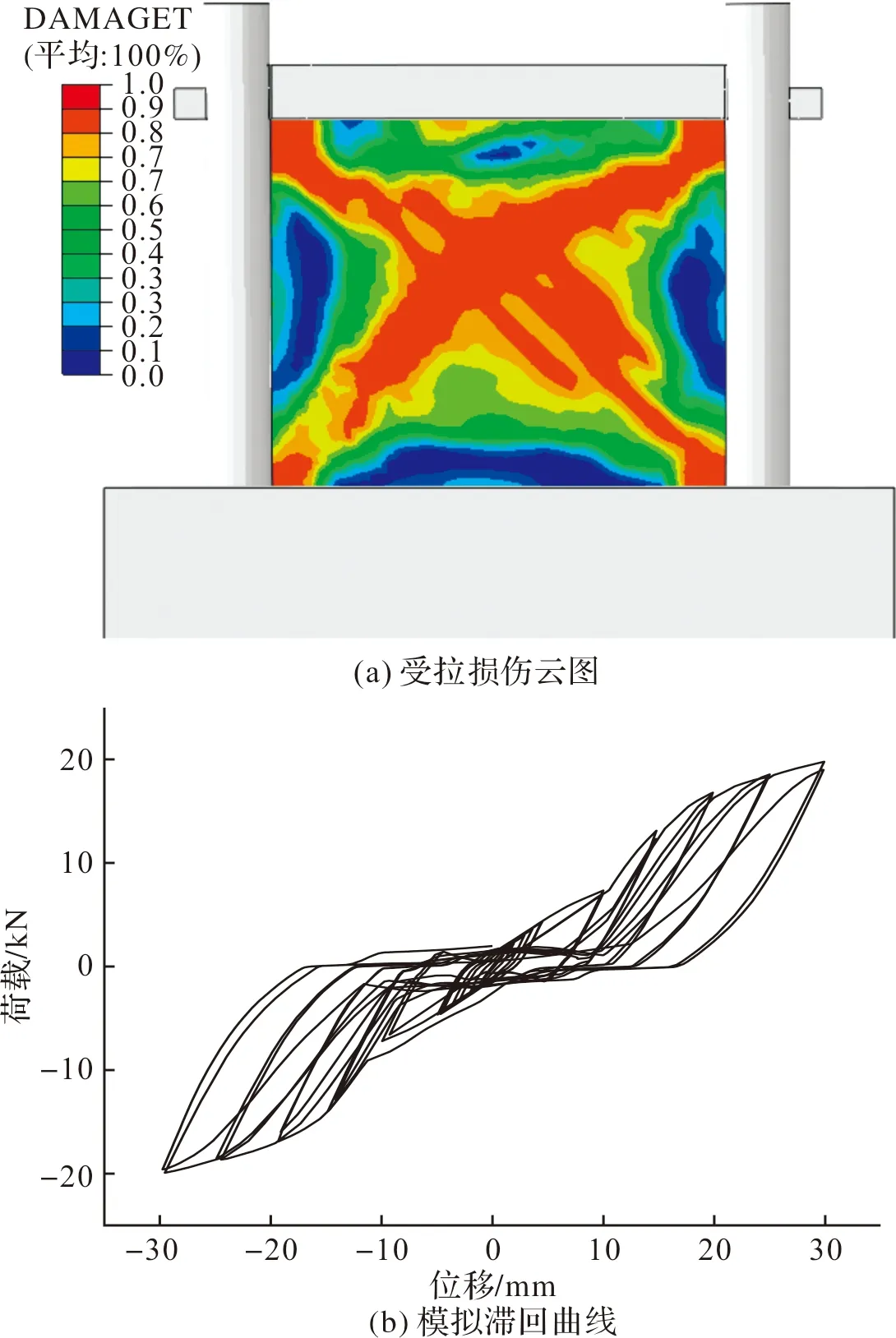
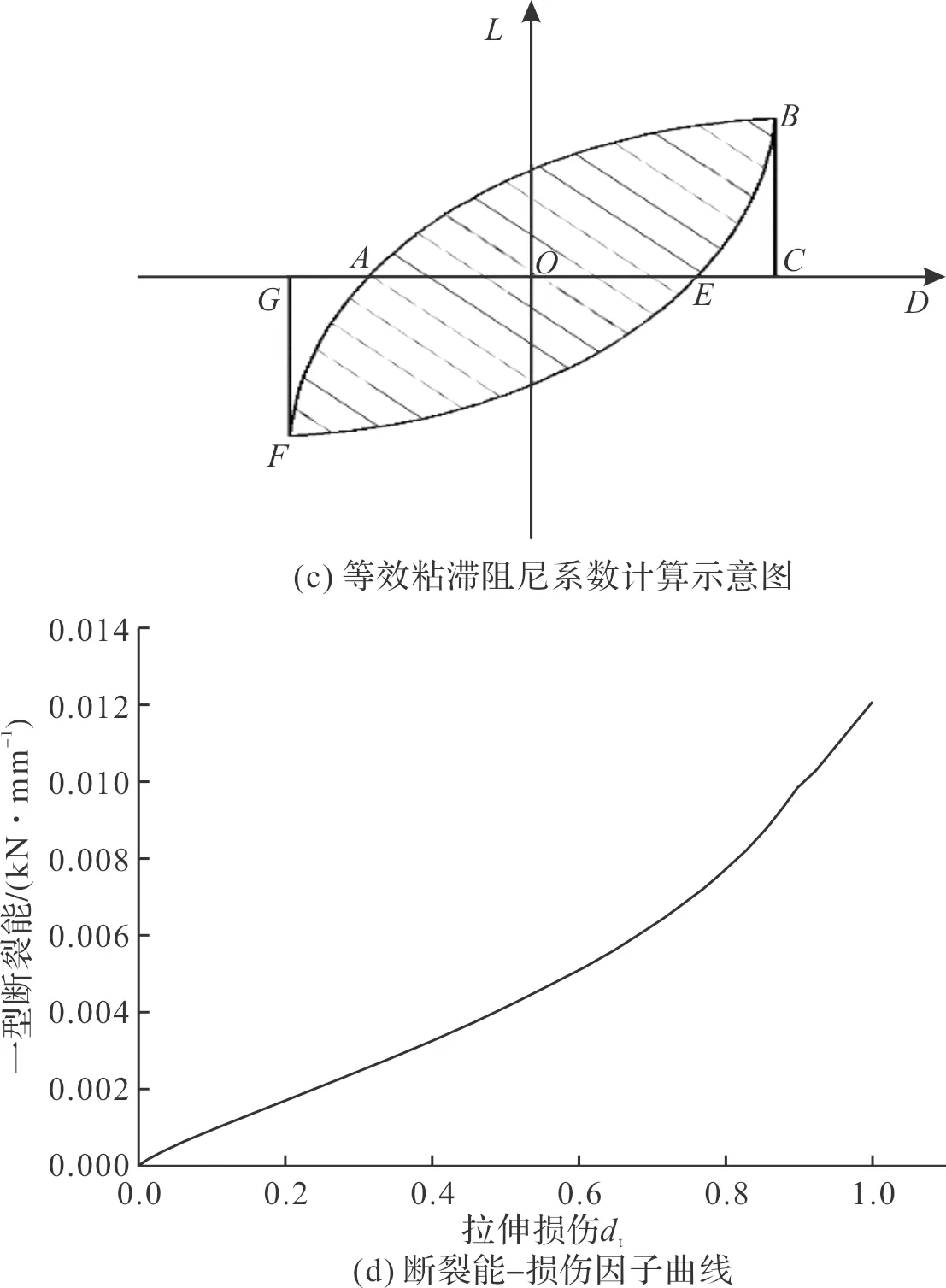
图7 一榀带填充墙穿斗式木构架平面内循环加载模拟结果Fig.7 Simulation results of in-plane cyclic loading of a column-and-tie wooden structure with infilled wall

(6)

通过FE模拟，得出了带填充墙的台阶透榫式穿斗式木构架的拉损伤云图与滞回曲线，如图7(a)、(b)所示.损伤首先发生于填充墙的四角，随着加载的进行，在填充墙的中部出现斜裂缝并逐渐向四角发展，最终形成“X型”裂缝.由于填充墙与框架之间仅靠摩擦传力，在试件加载时便会产生相对滑移，因此滞回曲线有“捏缩”现象，滞回曲线形状为Z形也证实了试件受到大量的滑移影响.在试件加载初期，填充墙处于弹性阶段，未达到屈服状态，卸载之后残余变形很小，滞回环面积很小，因此滞回曲线中部较为密集.当填充墙达到塑性阶段开始产生残余应变，内部损伤开始累积，滞回曲线面积开始增大，耗能能力开始提升，滞回环面积小、不饱满，表明试件的平面内耗能能力较弱，抗震性能欠好.

在工程中等效粘滞阻尼系数ξeq的大小通常被用来判断结构的耗能能力并据此评价结构的耗能性能.等效粘滞阻尼系数ξeq越大，耗能能力越强.其等效粘滞阻尼系数ξeq计算公式如式(7)，计算示意图如图7(c)所示，由此计算出不同位移下试件的等效粘滞阻尼系数.

(7)

计算得出以位移为增量的第1～6个滞回环的等效粘滞阻尼系数分别为0.141、0.160、0.095、0.092、0.087、0.085，其随着水平方向的位移增大表现出先增大后减小的趋势，后几环减小的幅值越来越小.这是因为前两个循环试件还未产生滑移，因此耗能能力较强，对应着中部“梭形”滞回曲线；后四个循环试件随着损伤的产生而出现明显的粘结滑移，因此耗能能力明显减小，对应着“Z形”滞回曲线，表明填充墙与框架之间的粘结滑移会影响试件的耗能性能.

2.2 平面外静力推覆模拟

平面外加载方式通过位移控制加载.建立250 mm×250 mm×10 mm大小加载垫块，位于填充墙中心，相对位置如图11(b)所示，加载垫块与墙体之间采用罚摩擦接触与硬接触模拟.距垫块中心面外偏离50 mm建立参考点并与垫块耦合，施加面外15 mm位移荷载.

FE模拟得出试件面外静力加载损伤云图与荷载-位移曲线如图8(a)、(b)、(c)所示.

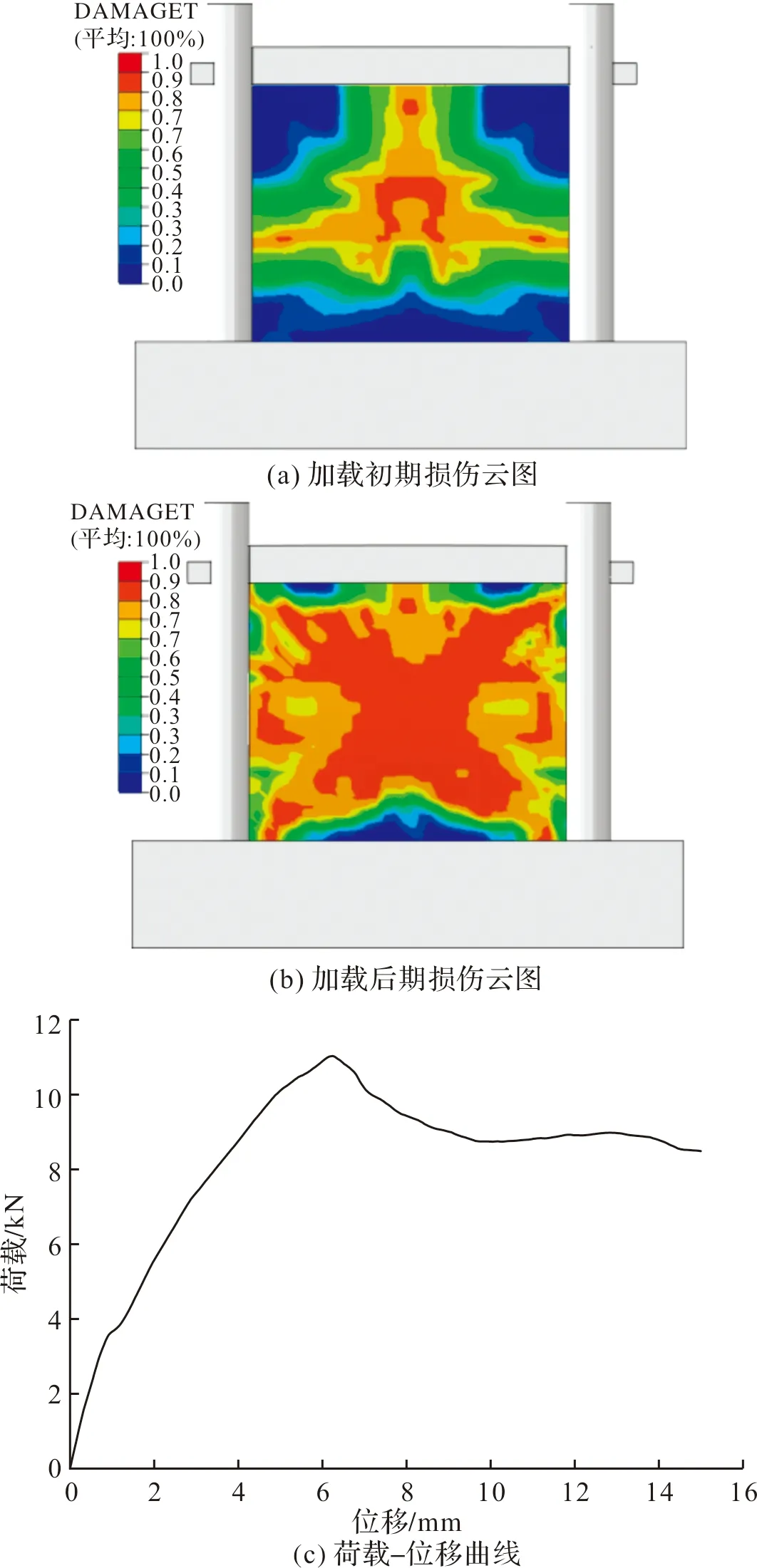
图8 一榀带填充墙穿斗式木构架平面外静力推覆模拟结果Fig.8 Simulation results of out-of-plane loading of a column-and-tie wooden structure with infilled wall

损伤首先发生于填充墙的中心，在加载初期呈现“倒Y”型损伤，为三边约束边界破坏模式，表明填充墙顶部与枋之间接触不好；继续加载，随着试件形变破坏模式由“倒Y”型转变为“X”型，裂缝由中部向四角发展，为四边约束边界破坏模式，表明填充墙顶部与坊之间已完全接触.面外位移约为6.23 mm时面外承载力达到峰值，约为11.03 kN，随后进入软化阶段，平面外耗能能力约为123.8 kN·mm.

3 ECC单面加固填充墙数值模拟

ECC是一种高韧性的新型水泥基复合材料，极限拉伸应变是普通混凝土的300倍以上.Meng等[37]经过大量ECC拉伸试验，将 ECC的受拉阶段分弹性阶段、多缝开裂阶段和应变硬化阶段.Feenstra等[38]将ECC的受压过程用断裂能表示，并用抛物线的形式表示受拉受压曲线.ECC材料的拉压断裂能均应为不变量，但由于在受拉应力状态下ECC呈现出应变硬化，在达到峰值应力后迅速失去承载能力，软化不明显，因此ECC受拉应力状态采用应力应变关系定义；而在受压应力状态下ECC在达到峰值应力后软化明显，在不同单元特征长度下应采用不同的应力应变关系曲线以保证受压模态断裂能Gc为常数.ECC的受压应力-应变曲线和受拉应力-应变曲线如图9 (a)～(b)所示.ECC性能参数如表3所示.

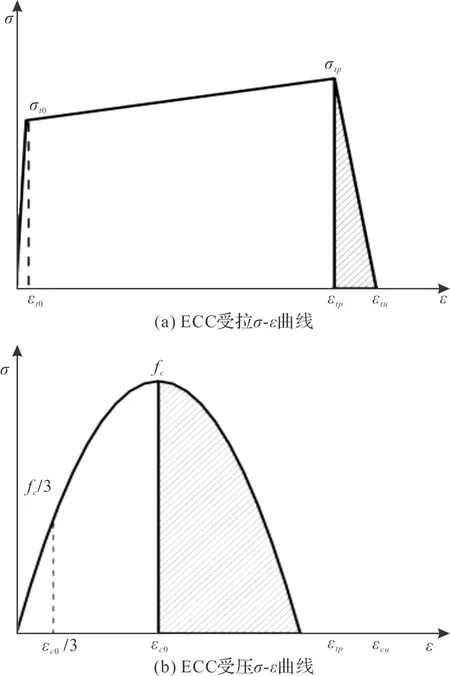
图9 ECC应力-应变曲线Fig.9 ECC stress-strain curve

表3 ECC性能参数Tab.3 ECC Performance Parameters

ECC受拉本构计算方程为[37]

(8)

式中：σt为ECC的受拉应力；σt0为初裂时拉应力；ε为ECC在受拉应力状态下的应变；εt0为初裂拉应力相对的应变；σtp为极限拉应力；εtp为极限拉应力相对的拉应变；εtu为极限拉应变.

ECC受压本构计算方程为[38]

(9)

(10)

采用20 mm厚ECC单面敷面加固填充墙，进行试件的平面内外加载模拟研究其加固效果.采用tie接触模拟ECC与填充墙的界面，即不考虑二者间的相对滑移.

3.1 ECC加固填充墙平面内抗震性能分析

ECC单面加固填充墙平面内加载损伤云图与曲线对比如图10(a)、(b)所示.采用相同的加载方式，未加固损伤云图图7(a)与ECC单面加固后损伤云图图10(a)有较明显差异，从云图对比中可以看出ECC有效抑制了填充墙裂缝的发展.ECC加固对比加固前后的滞回曲线如图10(b)所示，试件的峰值承载力仅提升2.7%，刚度略有提高，耗能提升不明显.因本文ECC单面加固仅加固填充墙而未考虑框架与填充墙之间的整体加固，而滞回曲线捏缩的主要原因是填充墙与木构架间的滑移，而此种方法并未从根本上解决此原因，因此仅加固填充墙的方法对平面内抗震能力提升不明显.

图10 ECC单面加固平面内加载Fig.10 In-plane loading with ECC single-side reinforcement

3.2 ECC加固填充墙平面外抗倒塌性能分析

ECC加固试件受拉侧损伤云图及荷载-位移曲线如图11(a)、(b)、(c)所示.由图(a)、(b)云图可知，ECC单面加固填充墙受拉侧后破坏模式与未加固破坏模式一致，为损伤从中部发生并向四周扩展，但加固后试件损伤程度明显小于未加固试件.未加固填充墙平面外极限承载力为11.03 kN，采用单面ECC加固填充墙受拉侧后填充墙平面外极限承载力为30.72 kN，提升了1.785倍.将荷载-位移曲线与坐标轴围成的面积作为耗能评价指标，得出未加固的试件耗能为123.8 kN·mm，加固后的试件耗能为309.5 kN·mm，提升1.5倍.由此可以看出采用ECC单面加固填充墙的方法对平面外的承载力及耗能提升作用明显.

图11 ECC单面加固平面外加载Fig.11 Out-of-plane loading with ECC single-side reinforcement

4 不同损伤程度下的加固后结构平面外抗倒塌模拟研究

由于采用ECC单面加固的方式对试件平面外的承载力提升更为明显，而填充墙的损伤状态对加固效果的影响目前尚未有研究报道，因此拟进一步进行不同损伤状态下结构的平面外加固效果研究.根据Meng等[39]可采用试件所承受的荷载状态或与之对应的变形状态来模拟穿斗式木构架填充墙的损伤情况.本文为方便数值模拟的实现，以未加固带填充墙的穿斗式木构架的加载点所受荷载对应的位移量来模拟试件的损伤状态.

4.1 模拟方法

根据先前的试件数值模拟结果，当试件的上升段承载力为峰值荷载的20%时，试件已有裂缝产生.因此，本文以峰值承载力的20%所对应的位移点作为第一个计算工况，定义该工况为轻微损伤状态；以峰值承载力的100%所对应的位移点作为第五个工况计算，定义该工况为极严重损伤状态.将峰值承载力的20%～100%区间均等划分，分别取峰值荷载的40%，60%，80%所对应的位移点作为第二～四个计算工况，三个工况分别定义为中等、较严重、严重损伤状态.

采用ABAQUS软件中的生死单元功能来实现补强加固模拟，首先将加固层单元设为生死单元，在试件加固前将其钝化，对未加固试件施加以位移荷载.当试件达到相应损伤状态时将加固层单元激活，再对试件施加位移荷载直至破坏.

4.2 加固效果分析

针对ECC单面敷面加固方案不同时机下穿斗式木构架填充墙面外荷载-位移曲线见图12(a)，不同损伤状态下的加固效果有明显的不同.

图12 不同损伤状态下ECC单面加固结构模拟Fig.12 ECC single-side strengthened structure modelling under different damage levels

其中：轻微损伤状态下加固曲线走势与未损伤直接加固走势相似；较严重、严重、极严重损伤状态下加固后曲线走势相似；中等损伤状态下加固曲线未表现出明显的承载力走低趋势，表明耗能性能提升明显.在较严重、严重、极严重损伤状态下加固时，峰值承载力提升明显，分别提升了2.47倍、2.34倍与2.17倍；在轻微损伤与中等损伤状态下加固时，耗能能力提升明显，分别提升了2.04倍与1.98倍，提升曲线如图12(b)所示.综合考虑承载能力与耗能性能，在填充墙轻微或中等损伤时采用ECC单面加固效果最优.

5 结论

(1) ECC覆面加固穿斗式木构架民居结构是一种经济、环保的绿色低干预加固方法；

(2)带填充墙的穿斗式木构架的平面内耗能效果较为不好，滞回曲线存在“捏缩”现象，表明结构受面内横向荷载时存在大量滑移，亟待设置拉结筋等构造措施以提升面内的抗震性能；

(3)采用ECC单面敷面的加固方式对平面内承载力提升不明显，仅提升2.7%，而面外承载力提升1.7倍以上，表明此种加固方式可以有效提升结构平面外抗倒塌能力；

(4)带填充墙的穿斗式木构架在不同损伤状态下的加固效果有明显差异，ECC单面加固对不同损伤状态下的填充墙面外性能都有明显的加固作用，但在轻微损伤与中等损伤状态下加固效果更好.