教与学优化储备池计算的混沌时间序列预测

李志刚，高媛媛，孙晓川

(华北理工大学，河北 唐山 063200)

1 引言

混沌时间序列广泛存在于气象系统、天文系统、水文系统等复杂的自然系统中[1]。这些系统随时间的演变呈现出非线性、非周期性且伴有噪声的混沌特性。如何预测演变出混沌时间序列的变化规律是一项具有挑战性的研究课题[2-4]。

当前，机器学习成为预测混沌时间序列的主流方法，特别是人工神经网络(Artificial Neural Net-work， ANN)。其中，递归神经网络(Recurrent Neural Network， RNN)[5]凭借其记忆的特性，表现出良好的非线性逼近能力。但它训练算法复杂、网络结构难以确定，导致计算负担过重且容易陷入局部最优，极大地影响了它的预测能力。

为解决以上问题，Jaeger 教授在 2001 年提出回声状态网络(Echo State Networks， ESN)[6]，它的核心为随机产生且稀疏连接的储备池。ESN的学习过程简单，只需训练输出权值，呈现出计算量小且精度高的优势，成功应用于网络流量预测、模式识别、图像处理、事件检测等领域[7-8]。众所周知，ESN在构建网络时产生了众多参数，如谱半径、输入尺度、稀疏度、储备池规模等。由于它们在初始化中随机产生，使得网络适应性和稳定性降低，影响网络的泛化性能，特别是输入权值、储备池内部权值和反馈权值的随机初始化对网络性能影响较大。

针对ESN的输入权值、储备池内部权值和反馈权值的参数选择问题，大量的优化算法被研究[9-14]。粒子群优化算法(Particle Swarm Optimization， PSO)[15]凭借其较强的全局搜索能力和较高的计算精度，被广泛用于优化ESN参数。其中Wang等[16]采用二进制PSO算法优化输出权值来替代ESN的训练，提高了ESN的预测精度，但却忽略了模型的复杂度，影响模型的预测效率。然而，Chouikhi等[17]采用PSO算法对储备池规模和连通性进行单一参数和组合参数的优化，在模型复杂度和预测精度中权衡出最优的模型。尽管上述这些做法不同程度上弥补了ESN的预测能力，但优化参数的特征较多会导致网络随机性的丧失和预测速度的降低，选择适当的特征子集是优化参数任务中非常重要的工作。针对以上问题，Chouikhi等[18]用粒子群优化算法来优化部分输入权值、储备池内部权值和反馈权值并在多个时间序列中得到了验证。这样既保留了网络的随机性，又降低了模型复杂度，并且提高了预测精度。但由于粒子群优化算法存在参数较多、收敛速度慢、容易陷入局部最优解等问题，降低了它的收敛效率。

为了有效处理全局优化，探寻简单而高效的优化算法，提高ESN的预测效率，R. Rao等[19]提出了教与学优化 (Teaching-learning-based Optimization， TLBO)，它是一种基于种群的求解非线性连续问题的随机方法，它的灵感来自于一个典型班级的教学过程。具有参数少，简单易行，收敛速度快，稳定性强，计算精度高，全局搜索能力强等优势，可以有效地弥补PSO的不足[20]。

鉴于此，本文对ESN的参数选择问题展开了研究，具体是指利用TLBO算法来优化ESN中初始化且固定不变的输入权值、储备池内部权值和输出权值，以提高ESN的预测性能。同时，为了降低优化模型的复杂度，减少训练时间，并保留以上参数的随机性，本文采取部分优化的方式来获得最优复杂度模型结构，保留优化参数的随机性，以获得一种具有最优复杂度和随机性的高效预测模型TLBO-ESN。进一步，将其与相关PSO优化方法作对比并采取Mackey-Glass和Lorenz混沌时间序列验证模型的有效性。

2 教与学优化的回声状态网络

本文提出的TLBO-ESN是用TLBO来自适应选择局部的输入权值、储备池内部权值和输出权值参数，不仅保留了网络的部分随机性，并且提高了模型的预测性能。

2.1 TLBO-ESN的网络结构

具有参数自适应性和随机性的TLBO-ESN模型结构如图1所示。将教与学优化的Win，W和Wfb用红色箭头表示，具有随机性的原始Win，W和Wfb用黑色箭头表示，使TLBO-ESN成为一种简单而高效的递归神经网络。与传统ESN相似，储备池内部的神经元采用随机产生并稀疏连接的方式，增强了模型的非线性映射能力。

图1 教与学优化的回声状态网络结构

网络的更新方程如下

x(t+1)=f(Winu(t+1)+Wx(t)+Wfby(t))

(1)

y(t+1)=fout(Woutx(t+1)+Winoutu(t+1))

(2)

其中，u(t)，x(t)，y(t)分别表示输入层，储备池和输出层在t时刻的状态。f和fout为储备池和输出层的激活函数，它们可以是线性函数，也可以是非线性函数，常见的有Tanh，Sigmoid等。将Winout和Wout定义为输出权值矩阵R，R需要在训练中更新

R=pinv(M)*yt

(3)

其中M是储备池内部神经元的状态矩阵，pinv(M)是M的伪逆矩阵，yt是输出层神经元状态矩阵。所以，求解输出权值矩阵R就转化为了简单的线性问题。

2.2 教与学优化策略

首先，选取部分Win，W，Wfb作为待优化对象partWeight

partWeight=αψin+βψ+γψfb

(4)

其中ψin，ψ和ψfb是Win，W，Wfb中的非零元素，参数α，β，γ是设定的参数，范围[0，1]。

适应值函数也称“目标函数”，用来评价优化对象的优劣，本文采用均方根误差(Root Mean Squared Error， RMSE)作为适应度函数

(5)

其中，N为输出样本大小，yt(t)为t时刻的期望输出，y(t)为t时刻的实际输出。

将待优化对象partWeight赋值给NP个学生，组成班级S=x1，x2，…，xNP，令迭代次数为G，班级中的每个学员的位置为xi(i=1， 2，…，NP)，根据适应度函数RMSE，每位学员有成绩Xi(i=1， 2，…，NP)，通过优化输出成绩最佳的xi(i=1， 2，…，NP)。

优化分为两个阶段：教师阶段和学生阶段。

在教师阶段，将整个班级中成绩最佳的当作教师xteacher， 教师通过式(6)传授经验给学生来提高整个班级的成绩

(6)

其中，xiold和xinew分别表示第i个学员学习前和学习后的位置，mean是所有学员的平均位置；还有两个关键的参数，即教学因子TFi=round[1+rand(0，1)]和学习步长ri=rand(0，1)， 因为每个学生的学习能力不同，因此教学因子TFi和学习步长ri应针对不同学生进行设定，使算法具有特异性。

在学习阶段，学生通过互动交流学习，进一步提高自己的成绩。每个学员xi(i=1，2，…，NP)在班级中随机选取一个学习对象xj(j≠i)，xi通过式(7)分析自己和xj的差异进行学习调整：

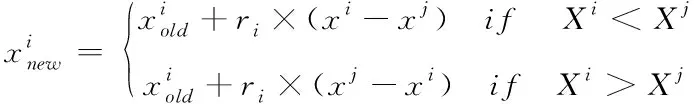
(7)

其中ri=rand(0，1) 表示第i个学员的学习步长。

2.3 训练步骤

与传统的ESN训练不同，TLBO-ESN在训练前需将部分Win，W，Wfb进行迭代寻优，用优化好的Win，W，Wfb参与传统的ESN训练。TLBO-ESN的训练步骤如下所示。

算法：TLBO-ESN的训练

1)初始化ESN的参数；初始化partWeight；

2)xi( i=1：NP )=partWeight；

3)NP=8， G=50；

4)while G < 50 do

5)Xi( 1 ：NP)=RMSE；

6)xteacher=适应值最佳的xi；

7) 教师阶段：

8) for i=1： NP do

9)xinew=xiold+ri× (xteacher-TFi×mean) ；

10) end for

11) 更新学生成绩；

12) 学生阶段：

13) 随机选取xj( j≠i )；

14) for i=1： NP do

15)ifXi

16) xi new=xi old+ri× (xi-xj)；

17) else

18) xi new=xiold+ri× (xj-xi)；

19) end if

20) end for

21) 更新学生成绩；

22)end while

23)partWeight=xi( i=1：NP )；

24)将partWeight加入到网络中；

25)根据式(1) (2)更新网络状态；

26)根据式(5)求训练误差；

27)根据式(3)求输出权值R。

3 实验分析

本文考虑了Mackey-Glass和Lorenz混沌时间序列数据集，选取PSO-ESN、RandWPSO-ESN、LinWPSO-ESN、LnCPSO-ESN、AsyLnCPSO-ESN来评估TLBO-ESN的有效性和优越性。

表1 模型的参数配置

表1给出了Mackey-Glass和Lorenz基准下模型的参数配置，这些参数通过网格搜索法确定。

为了得到较好的预测结果，使用500个数据样本作为训练集，500个用于测试。为了避免某些参数随机初始化对网络性能的影响，将算法重新执行5次后取平均值作为最后的结果。

本实验分别从预测精度、收敛速度和稳定性三个方面来度量教与学优化回声状态网络模型的整体性能。其中，预测精度通过测试误差RMSE即式(5)作为评价标准，收敛速度用训练时间评估，稳定性以极差(Range， R)和平均绝对偏差(Mean Absolute Deviation， MAD)为准。

3.1 数据描述和度量标准

Mackey-Glass时间序列

具有延时特性的Mackey-Glass混沌时间序列的动力学方程为

(8)

其中，通常取a=0.2，b=0.1，c=10，参数τ为延时因子，决定混沌程度。当τ>16.8时系统出现混沌特性，τ的值越大混沌性越强。本实验τ取17。

Lorenz时间序列

Lorenz引力是描述流体在热表面和冷表面之间运动的一组微分方程，描述公式如下：

(9)

其中，当参数α=10， r=28， b=8/3时，系统出现混沌特性。

3.2 性能分析

为了更加准确的评估模型的性能，本实验分别讨论了在谱半径和储备池规模参数的动态变化下各个模型的性能。图2和图3给出了各模型在执行Mackey-Glass和Lorenz时间序列预测任务的性能对比。其中谱半径的变化范围为(0，1)，储备池规模的变化范围为(50，100)。从图中可以直观地看出，在测试误差相同的变化范围内，TLBO-ESN的变化波动最小，可见它对储备池规模和谱半径的敏感度最低。

图2 Mackey-Glass序列下模型的误差对比

图3 Lorenz序列下模型的误差对比

表2 模型的性能对比

表2给出了不同储备池规模和谱半径设置下各评估模型的最优预测性能。显然，无论是Mackey-Glass时间序列还是Lorenz时间序列，TLBO-ESN的测试误差均小于其它模型，并且训练时间最短，模型的复杂度最低，预测效率最高，因此TLBO-ESN的测试性能最佳。

为了进一步讨论模型的稳定性，在统一模型的配置下(表1)，对每个模型分别做100次实验，统计各模型测试误差的变化情况。

表3 模型的稳定性对比

表3给出了不同模型在执行预测任务中测试误差的极差(Range， R)和平均绝对偏差(Mean Absolute Deviation， MAD)。极差表示测试误差的波动范围，平均绝对偏差表示测试误差的离散程度。可以看出在执行Mackey-Glass和Lorenz的预测任务中，TLBO-ESN测试误差的极差和平均绝对偏差最小，因此它的测试误差变化范围和离散程度最小，模型的稳定性最强。

为了进一步讨论模型的收敛能力，在统一参数配置下(表2)，本实验总结了各模型在执行预测任务中适应值随迭代次数的变化，其中适应值由式(5)求出。

图4 模型的收敛性对比

图4给出了各模型在执行Mackey-Glass和Lorenz混沌时间序列预测任务下的收敛性能对比，描绘了不同算法在迭代过程中适应度变化趋势。可以看出TLBO-ESN都是最快达到收敛且适应度值最小。因此TLBO-ESN的收敛速度最快，收敛效率最高，收敛性能最强。

4 结束语

本文在储备池计算框架下，利用教与学优化算法来选择回声状态网络的部分Win，W和Wfb以适应于不同混沌时间序列的动力学特性， 提高了预测精度，保留了网络的随机特性，仿真结果表明，在执行混沌时间序列任务中，本文所提出的模型比其它预测模型具有较高的预测精度和较强的收敛性能，并且保留了模型的随机性。本实验将丰富储备池计算优化研究的内涵，对于推动其应用于预测混沌时间序列具有重要意义。通过与五种粒子群优化算法的对比实验表明，TLBO-ESN的性能最佳，模型具有较好的预测精度、收敛速度和稳定性。下一步研究的主要内容是对于模型预测多种时间序列问题的性能。