双水平集算法及其在函数轮廓估计中的应用
李晓杉,夏界宁
(1. 中国地震局地震研究所地震预警湖北省重点实验室,湖北 武汉 430071;2. 湖北省重大工程地震安全监测与预警处置工程技术研究中心,湖北 武汉 430071)
1 引言
水平集估计(Level Set Estimation, LSE)问题,即在某个空间上寻找信号大于某个门限值的点集。在信号采集过程中,只有非常有限的信号样本点可用,且这些样本含有噪声,这就使得无法逐个“遍历”每个样本点,而必须使用有限且含有噪声的样本进行分析[1-5]。在进行数据采样及分析时,如果观测样本有限或者观测难度较大时,需要关注样本点的统计特性,高斯过程具有十分良好的特性,因此,利用高斯过程进行目标函数的建模[6]。LSE算法本质上与二元分类算法相似,是一种单调分类的算法[1]。利用LSE算法,能够在观测值有限的情况下有效地进行数据分类与预测。
水平集估计问题在函数最优化[1]、遥感图像处理[7]、医学图像处理[8]、数据聚类分析[9]等领域得到了广泛应用。
文献[1]中B. Bryan等人对小样本情况下的函数阈值边界问题进行了分析,利用高斯过程对目标函数进行建模,对比了不同方法的效果,并进行了数值实验,将参数估计问题所需的样本数和计算量减少了一个数量级[1]。文献[2]中A. Gotovos等人建立了LSE算法框架,并进行了数据实验,利用LSE算法对实际问题进行了处理,实现了小样本空间下的数据分析,同时对LSE算法进行了扩展,针对隐含式阈值边界及批量选择样本情况进行了延伸,并且进行了收敛性理论分析[2]。文献[3]中Y. Ma等人使用高斯过程对函数建模,并使用贝叶斯积分来推断其在感兴趣区域上的平均值,针对有效区域搜索(Active Area Search, AAS)问题进行了分析,比以前提出的相关方法更快地识别出正区域[3]。文献[4]中I. Bogunovic等人利用高斯过程处理贝叶斯优化和水平集估计问题,提出了截断方差减少(Truncated Variance Reduction, TRUVAR)算法,可以纳入近视算法。与执行超前的其它贝叶斯优化(Bayesian Optimization,BO)算法相比,TRUVAR算法避免了计算上复杂的对后验和测量进行平均的步骤,并且具有严格的理论保证[4]。文献[5]中Andrea Zanette等人提出了水平集估计的鲁棒最大改进(Robust Maximum Improvement for Level-set Estimation, RMILE)算法,对LSE算法进行了改进,在一步先行程序中选择最大化高于阈值点域的预期体积的下一个查询点,并导出分析公式以封闭形式计算该数量,能够更有效地使用从少量样本中获得的信息,使其适用于非常有限的样本点,且保证了渐近收敛性,使其在特定模型的情况下得到了有效结果[5]。
与其它分类算法相比,D_LSE算法的查询点少、受噪声影响小,在解决有限且含噪声数据的分类问题时具有优势。与传统的LSE算法相比,D_LSE算法考虑了两个阈值,更适用于小样本空间下的双水平集估计问题。这一研究具有一定工程应用价值,例如在重力测量方面,绝对重力的测量成本高、难度大,重力数据有限且含有噪声。相比于获得每个测量点的具体重力值,某个区域的重力分部更加重要,希望将重力值划分为多个等级,此时单一阈值无法满足研究需求,需考虑多阈值分类的算法。相比于之前的研究,考虑了分类精度参数ε对算法的影响。本文首先给出了D_LSE算法的理论依据,其次进行数值实验,最后利用D_LSE算法解决函数最优化问题,展示D_LSE算法的实用性。
2 D_LSE算法
当数据点(观测值)的获取难度比较大或成本昂贵时,无法对数据进行逐个遍历,必须对数据的统计特征进行分析。D_LSE算法利用高斯过程对函数建模,能够有效描述数据的统计特征[10]。通过对高斯过程的样本进行分类,分为上水平集、中水平集和次水平集,并进行不断更新,能够实现函数的估计(分类)。
2.1 D_LSE算法概述
就A. Gotovos的原LSE算法做出扩展,原LSE算法考虑单一阈值问题,应用单一水平集进行区域的分类,把区域分为超水平集(Super-Level Set)与次水平集两部分。将此问题进行扩展,考虑多阈值问题,应用多个水平集,将观测值分为多个区域。
D_LSE算法的原理是构建一个三维曲面,将二维问题转化为三维曲面的水平集估计问题。以高斯过程逼近采样点与曲面的映射关系,不断对置信边界进行引导采样和分类。
假定估计函数f:D→;采样点x∈D;两个阈值h1∈Rd,h2∈Rd,且h1 (1) 双水平集的示意图如图1。将这种方法扩展到多水平集的情况下,可用来处理多阈值问题。 图1 双水平集示意图 D_LSE算法主要有初始化、计算置信区间、分类、更新、选取查询点五个步骤。 2)计算置信区间:对于未分类的样本点,用当前的高斯过程计算样本点的置信区间。 假定每次只分类单个数据点,则对于任意t≥ 2,数据点xt∈D,噪声测量值yt=f(xt)+nt,其中nt为零均值高斯白噪声,方差为σ2。若GP的先验g(0,k(x,x′)) 超过f;并给出At={x1,…,xt}中t点的噪声测量值yt=[y1, …,yt]T,其中yi=f(xi)+ni,且ni~N(0,σ2),i=1, …,t。根据高斯过程的性质,后验仍是高斯过程,因此,能够通过如下公式对所拟合的高斯分布进行更新 μt(x)=kt(x)T·(Kt+σ2I)-1·yt (2) kt(x,x′)=k(x,x′)-kt(x)T·(Kt+σ2I)-1·kt(x) (3) (4) 其中kt(x)=[k(x1,x), …,k(xt,x)]T,且Kt是即将观测点的核矩阵 Kt=[k(x,x′)];x,x′∈At (5) 由式(2)、(4)可推断出置信区间如下 (6) 对置信区间取交集,Ct(x)表示每个x的单调递减的置信区域 (7) 3)分类:通过置信区间与上阈值、下阈值的关系对该点进行分类。定义集合Ut表示未分类的点集;Ht表示超水平集,包含高于上阈值h2水平的点;Mt表示中水平集,包含高于下阈值h1且低于上阈值h2水平的点;Lt表示次水平集,包含低于下阈值h1水平的点。 4)更新:依据式(2)、(4)、(7)更新未分类点的高斯过程与置信区间,并进行分类。 5)选取查询点:若存在未分类的点,则需要依据最大模糊度准则选择新的查询点来获取信息,直至所有点均完成分类。 D_LSE算法为一种单调分类的算法,在分类错误的情况下无法进行修改。因此以置信区间引入模糊度: (8) 模糊度的示意图如图2。模糊度越大的点越接近阈值,包含更多信息,因此以模糊度最大准则选取查询点。 图2 模糊度示意图 算法1:D_LSE算法 输入: 采样集D,高斯先验参数(μ0=0,k,δ0),上阈值h2,下阈值h1,精度参数ε。 1)H0←∅,M0←∅,L0←∅,U0←∅, C0(X)←,forallx∈D 2)t←1 3)whileUt-1≠∅do 4)Ht←Ht-1,Mt←Mt-1,Lt←Lt-1, Ut←Ut-1 5)forallx∈Ut-1do 6)Ct(x)←Ct-1(x)∩Qt(x) 7)ifmin(Ct(x))+ε>h2then 8)Ut←Ut{x},Ht←Ht∪{x} 9)elseifmax(C0(x))-ε≤h2and min(Ct(x))+ε>h1then 10)Ut←Ut{x},Mt←Mt∪{x} 11)elseifmax(C0(x))-ε≤h1then 12)Ut←Ut{x},Lt←Lt∪{x} 13)xt←arg maxx∈Ut(at(x)) 14)yt←f(x)+nt 15) 对所有x∈Ut, 计算μt(x)andσt(x) 16)t←t+1 互信息I(X:Y)可用来表示X中包含Y中信息的多少[10]。在D_LSE算法中,考虑t个观测值yt=(yi)1≤i≤t和估计函数f的互信息如下 I(yt:f)=H(yt)-H(yt|f) (9) 其中H(yt)为观测值的熵,H(yt|f)为条件熵。 为了从观测值yt中获得更多估计函数f的信息,最大化互信息I(yt:f) (10) 高斯分布的熵定义如下 (11) 假定信号服从高斯分布,且噪声为高斯白噪声,则由式(13)、(15)可得 (12) 为了衡量分类的质量,引入错误分类损失 (13) lh(x)的最大值反映了分类的质量,max(lh(x))越小则分类质量越高。对于准确度为ε的分类,若max(lh(x))≤ε,则可以认为分类在ε精度的条件下是完全正确的,即分类是ε精确的。 考虑D_LSE算法的迭代次数T来分析算法的复杂度。对于阈值h∈,精度参数ε>0,α∈(0,1),D_LSE算法的最大迭代次数T满足如下不等式 (14) 此时,算法有1-α的概率达到ε分类精度 (15) 首先完成D_LSE算法的MATLAB程序验证,接着给出其F1分数评价,最后修改实验参数进行对比,并进行分类结果质量评估。 参考文献[1]中的函数模型,其目标阈值边界具不连续、存在模糊区域、存在函数远离阈值区域、长度足够的特点,因此能够避免算法在在这些区域过采样[1]。函数的三维模型如图4所示,考虑的函数模型如下 f(x,y)=sin(10x)+cos(4y)-cos(3xy) (16) 相关参数设置如下: 对于双水平集问题,可以看作是两层二元分类问题。若仅仅使用分类准确率这一指标评估分类质量,则在出现数据不平衡问题时效果很差,例如有100个样本点,其中99个为正,1个为负,而直接预测所有点都为正,这样虽然准确率达到99%,但预测是不具有高质量的。对于二分类问题,F1_score方法能够很好地评估其分类质量[11-12]。对于阈值h2,假定超水平集H为正,中水平集M为负;对于阈值h1,假定中水平集M为正,次水平集L为负。精确率与召回率的定义见表1和表2。 表1 阈值h2分类结果评估方法表 表2 阈值h1分类结果评估方法表 3.4.1 对比实验 1)实验参数1:h1=-0.5,h2=0.3,采样点25*50=1250,精度参数ε=0.3,实验结果如图3。 图3 参数1实验结果 查询点数t=132;运行时间405.65秒。 2)实验参数2:h1=-0.5,h2=0.3,采样点25*50=1250,精度参数ε=0.1,实验结果如图4。 图4 参数2实验结果 查询点数t=532; 运行时间9611.15秒。 3)实验参数3:h1=-0.5,h2=0.3,采样点10*20=200,精度参数ε=0.3,实验结果如图5。 图5 参数3实验结果 查询点数t=91; 运行时间39.51秒。 3.4.2 函数最优化问题实验 不断地增大和减小阈值,能够不断接近实际函数的最大值和最小值。相比于传统求函数最值的方法,此方法并没有对函数凹凸性的限制,即可得到全局最优结果。 设定参数为:采样点25*50=1250,精度参数ε=0.1,实验结果如图6。 图6 函数最优化问题实验结果 D_LSE水平集估计结果表明其能够有效估计函数的真实轮廓。最终分类结果的F1得分接近于1,表明分类质量较高。 通过改变相关参数:采样点数、精度参数进行对比。精度参数ε越小,最终F1得分越高,表明分类质量越高,但查询点数越多,程序运行时间越长;采样点数越多,分类质量越高,但查询点数越多,程序运行时间越长。不断增大/减小阈值,能够有效逼近函数的全局最大/最小值,解决函数全局最优化问题。 本文提出了小样本空间下的双水平集算法,主要结论有:1)考虑了两个不同的阈值,以高斯过程描述信号的统计特性,采用构造三维隐曲面的方法完成二维曲线的估计,提出了一种双水平集估计算法;2)将D_LSE算法应用于函数轮廓估计问题中,且以数值实验验证了算法的有效性;3)讨论了采样点数和分类精度参数ε的对算法的影响,并进行了对比实验,采样点数越多、精度参数ε越小则算法质量和复杂度越高;4)将D_LSE算法应用于函数最优化问题,证明了算法在最优化问题上的可行性。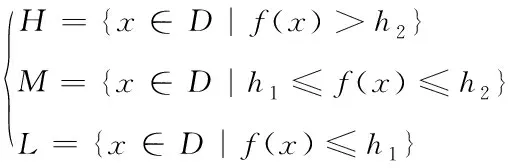




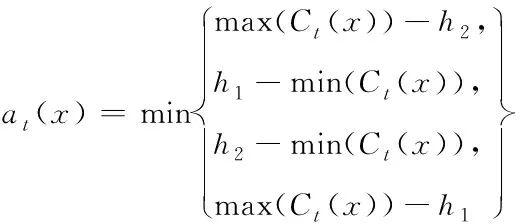

2.2 算法流程
2.3 精度与复杂度分析








3 仿真与结果分析
3.1 目标函数的建模

3.2 D_LSE仿真

3.3 算法分类质量评估




3.4 实验结果




3.5 实验结果分析
4 结束语

