土壤重金属元素含量的预测方法仿真研究
倪碧珩,陆 胤,施维林*
(1. 苏州科技大学环境科学与工程学院,江苏 苏州 215009;2. 浙江树人大学生物与环境工程学院,浙江 杭州 310015)
1 引言
土壤作为环境保护的特定要素之一,它的状况直接影响人类的健康[1]。但随着城市经济的快速发展,各类污染与化学物质与日俱增,导致土壤中的重金属含量不可控制,因此,对土壤中重金属元素含量进行预测,对人类的健康发展具有重要意义[2]。
黄赵麟[3]等人提出基于多模型优选的土壤重金属元素含量预测方法,该方法通过BP神经网络模型建立(BP-S),(BP-K),(BP-SK)模型,利用得到的模型模拟了土壤重金属元素含量的具体分布,实现土壤重金属元素含量的预测。该方法没有考虑多变量数据之间存在的相关性,增加了问题分析的复杂度,导致最终结果与实际结果偏差较大。陆荣秀[4]等人提出基于改进即时学习算法的土壤重金属元素含量预测方法,该方法首先利用信息加权建模,了解变量之间存在的关联性,最后建立LS-SVM模型实现土壤重金属元素含量的预测。该方法没有针对土壤重金属元素之间的变量关系建立相应的指标体系,导致预测精度低。高文武[5]等人提出基于协同克里金插值法的土壤重金属元素含量预测方法,该方法首先通过方差分析原理分析了土壤元素含量的影响,然后运用协同克里金插值法计算出平均误差、均方根误差和标准化均方根误差,对插值结果进行评价,最终实现土壤重金属元素含量的预测。该方法缺少重金属元素含量的相关数据分析,造成资料收集片面,导致最终的误差偏大。
为了解决上述方法中存在的问题,提出基于Krigin插值法的土壤重金属元素含量预测方法。
2 统计数据分析
2.1 相关数据分析
Pearson相关系数又叫做积差相关系数,r为样本相关系数,p为总体相关系数。具体表达式如下

(1)

相关分析定义为确定两个参数之间是否存在一定的关联性,用系数r来表示。它有两个特点,一个是方向性,表现为正关联、负关联或零关联,另一个是强度,表示两个参数存在的密切关联性。当x,y同向时,r>0为正关联;当x,y反向时,r<0为负关联。具体的评判标准如下所列:|r|>0.95说明两个变量之间确定关联,|r|≥0.8说明两个变量之间高程度关联;0.5≤|r|<0.8说明两个变量之间中程度关联;0.3≤|r|<0.5说明两个变量之间很少关联相关;|r|<0.3说明两个变量之间几乎不关联;r=0说明两个变量之间不关联[6]。
2.2 主成分数据分析
在相关数据分析的基础上对土壤重金属数据进行主成分分析,利用Hessian矩阵,将收集的高维数据映射到特征方向上,找到最大的曲线回归方向[7]。Hessian矩阵由实值函数f(x1,x2,…,xn)表达,当实值函数f中所有的二阶导数都存在时,f的Hessian矩阵表达为
H(f)ij(x)=DiDjf(x)
(2)
其中,x=(x1,x2,…,xn),则存在下式

(3)


(4)

(5)
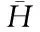
当向量x满足均值ux和协方差的正态分布时,uy就是y的均值,此时平均加权协方差矩阵就能够决定Hessian矩阵,如下列公式
(6)
向量x根据仿射变换标准化处理,得到满足标准正态分布的结果[9]。此时,土壤重金属数据的特征向量b1,…,bp可以根据下式得出
bp=λjbj,j=1,…,p
(7)
根据上式获取的特征向量,即为土壤重金属元素数据的主成分。
3 土壤重金属元素含量预测方法
3.1 重金属元素含量预测
基于Kriging插值法的土壤重金属元素含量预测方法采用Kriging插值法实现土壤重金属元素含量的预测。Kriging插值法就是将原始变量值转换为如式(8)所示的指示变量
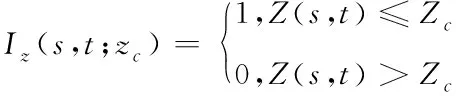
(8)
其中,Iz(s,t;zc)是Zc的引导值;Zc表示阈值;Z(s,t)表示为原变量值;t表示时间;s表示研究区域空间。
时间t全覆盖在研究区域内,不高于阈值Zc的积累概率可以根据相应指示值计算得出[10]
F(Zc)=Prob[Z(s,t)≤Zc]

(9)
其中,F(Zc)表示不高于阈值的积累概率;Prob[Z(s,t)≤Zc]表示小于阈值的积累概率;E[Iz(s,t,Zc)]表示在一定条件下的预期值。
在无抽样的情况下,在阈值以下的积累概率变量可以通过对样本点指示值的加权计算得到,Z(s,t)积累概率的最佳预测结果可以根据指示变量的最佳预测结果表示[11]。即
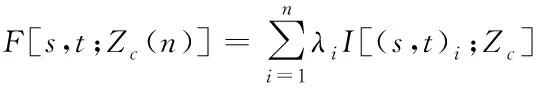
(10)
其中,F[s,t;Zc(n)]表示变量低于阈值的积累概率,λi表示对应条件下特定值的比例。上式中得到积累概率的最佳预测结果实际就是土壤重金属元素含量的预测结果。
3.2 预测结果优化
为了更好地得出最佳预测结果,需要计算出样本指示值的半变异函数
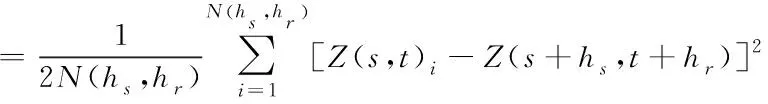
(11)
其中,γ(hs,hr)表示空间半变异函数;hs表示空间间隔变量,hr表示时间间隔变量;N(hs,hr)表示在空间和时间间隔内对应数据的点数;Z(s,t)i表示空间为s、时间为t的参数;Z(s+hs,t+hr)表示空间为s+hs、时间为t+hr的参数。通过上述时空半变异函数优化土壤重金属元素含量的预测结果。
3.3 含量等级划分
1)确定n个等级阈值Zc1,Zc2,…,Zcn,分别将变量归类为C0,C1,C2,…,Cn,其中,C0=(0,Zc1],C1=(Zc1,Zc2],…,Cn=(Zc1,∞]。将各个阈值根据式(8)进行指示变换,输出预测结果。
2)利用式(11)计算出与指示收集函数相关联的空间半变异函数,也可用中位值代表阈值的半变异函数代替每个等级阈值的半变异函数。
3)依次对等级阈值Zc1,Zc2,…,Zcn和各个空间单元使用Kriging插值法进行空间插值,算出各个等级划分中小于第n个阈值的概率P0,P1,P2,…,Pn及其误差预计的标准差sp1,sp2,…,spn。
4)根据预计概率和误差分别对各个空间单元进行归类判定。判定方法如下:
①计算预计概率的空间为[Pi-spi,Pi+spi]。
②当i=1,按照式(12)对空间单元进行等级判定:

(12)
其中,ci表示等级;Ci表示第i级;Ci-1表示第i-1级;C-1表示最末等级;Pci表示第ci个概率阈值;Pi表示第i个概率阈值;spi表示第pi个标准误差的标准差。
当i≠1,按照式(13)确定空间单元等级判定
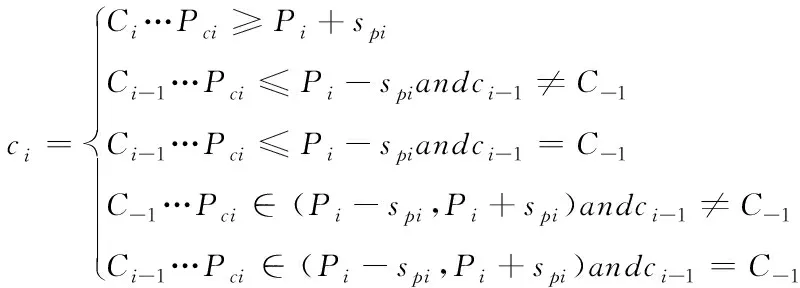
(13)
③判断所有阈值是否完成计算,如果完成则输出结果,如果没有完成则重回1)继续执行。
5)将同等级空间单元进行归类,形成等级边界。等级划分一般取决于概率估计值和概率阈值,大小由划分指数决定。一般情况下,两者越接近时误差越大,空间等级归类方法越易出错,其结果越不确定。
根据上述步骤,概率阈值对最终的结果起决定性作用,Kriging插值法计算结果小于阈值概率。在实验中,选取不同的概率阈值确定等级划分结果,将得到的最终结果与实际结果进行比较,得到不同概率阈值对应的误差指标,最终等级划分的概率阈值为最小误差指标对应的概率阈值,具体步骤如下列所示:
1)将概率阈值设定为0.1、0.2、0.3、…0.9;在特定的情况下,依次保留一个对应的原始样点,其他概率阈值则通过Kriging插值法对样点进行等级划分。
2)通过Kriging插值法计算的等级划分结果与真实结果进行对比,根据第一类错误T1、第二类错误T2、综合错误E进行对比判定,三类公式如下所示

(14)

通过最终结果得出最合适的概率阈值,在实验中得知概率阈值越大,第一类错误就会越大,第二类错误会减少,当实验结果中需要第一类错误最小,那么就控制概率阈值为0.1;第二类错误最小,概率阈值取0.9就会实现;如果让第一类和第二类错误接近,那么概率阈值就取0.5;如果划错比例控制最小,则概率阈值取0.4。
综上所述,基于Krigin插值法的土壤重金属元素含量预测方法首先利用Krigin插值法初步对土壤中重金属含量进行预测,其次通过半变异函数对预测结果进行优化,提高预测结果的准确率,最后设定阈值对重金属元素含量的等级进行划分,实现土壤重金属含量的预测。
4 实验与分析
为了验证基于Kriging插值法的土壤重金属元素含量预测方法的整体有效性,需要对其进行测试。分别采用基于Kriging插值法的土壤重金属元素含量预测方法(方法1)、基于多模型优选的土壤重金属元素含量预测方法(方法2)和基于改进即时学习算法的土壤重金属元素含量预测方法(方法3)在不同情况下对土壤重金属元素含量进行预测,预测结果如图1所示。


图1 不同方法的重金属含量预测结果
分析图1中可知,当距路基垂直距离不同时,方法1预测金属含量值与实际结果更吻合,方法2和方法3预测金属含量值与实际结果存在较大误差。因为方法1对多变量之间存在的相关性进行分析,并以此为依据对土壤重金属元素含量进行预测,降低了预测结果与实际结果之间存在的误差,提高了方法的预测精度。
图2为不同方法在重金属含量预测中均方根误差的对比结果。

图2 不同方法的均方根误差
分析图2中可知,邻近点数目不同时,方法1的均方根误差比方法2和方法3的均方根误差更小。因为方法1对变量进行相关分析时,建立了多指标分析体系,在一定程度上减少了信息的丢失,降低了误差。
图3为不同方法在重金属含量预测中不同概率阈值下错误比例的对比结果。

图3 不同概率阈值下的错误比例
分析图3可知,概率阈值不同时,方法1得出的错误比例比方法2和方法3更小,因为方法1在进行相关数据分析时,运用少量的综合指标对土壤重金属含量中的信息进行提取,保证了信息的真实有效,在一定程度上降低了错误比例。
5 结束语
土壤是人类获取食物的重要途径,与人类的身体状况密切相关。如今越来越多的土壤遭受重金属的污染,直接影响人类的身体健康,因此,提高土壤质量,加强土壤的管理与利用成为现阶段的重中之重。目前土壤重金属元素含量的预测中,存在预测精度低,信息大量丢失,资料收集片面的问题,提出基于Kriging插值法的土壤重金属元素含量预测方法,该方法首先对相关数据进行分析,总结出数据之间存在线性相关性,利用Kriging插值法建立预测函数,最终实现土壤重金属元素含量预测。该方法解决了以往方法中存在的问题,为土壤重金属元素含量预测仿真提供了全新的参考依据。

