基于KPCA和优化HMM的货车制动系统故障诊断

张鹏飞，岳建海，裴 迪，焦 静

(北京交通大学机械与电子控制工程学院，北京 100044)

1 引言

随着我国铁路货车运载量和速度的不断提高，制动系统作为保证货车安全运行的核心部件，保障其正常运行至关重要。但现有的铁路车辆运行安全监控系统(5T)中的货车运行故障动态图像监测系统(TFDS)只能对基础制动装置进行状态监测，无法实现对空气制动机气路故障的识别。目前，对于制动机故障大多采用人工检查，效率低，劳动强度大，且容易发生漏检。因此对货车制动系统状态监测具有现实且重要的意义。

针对列车制动系统故障诊断，主要有基于信号处理、基于解析模型和基于知识的方法[1]。随着制动机被设计的越来越复杂，单纯依靠信号处理的方法已不能准确诊断出故障。基于解析模型的方法有键合图模型[2]、物理模型[3]等，该方法的诊断效果依赖于模型的精度。基于知识的方法有专家系统[4]、神经网络[5]等，专家系统严重依赖获取知识的层次，神经网络依赖于样本数量和质量，而本文故障数据来源于货车线路运行过程，受制于数量原因，导致其诊断效果不佳。由于空气制动机结构复杂，各零部件间存在复杂的耦合关系，难以进行精确的建模，并且在状态监测中需要测量的变量较多，且变量之间存在相关性，导致故障诊断存在长时间序列和诊断性能低的特点。隐马尔可夫模型(HMM)基于时间序列建模，对小样本数据具有较好的诊断性，可用于任意时长的时序建模问题，广泛应用于行为识别、齿轮箱状态识别[6]、轴承故障诊断[7]等领域，这为HMM应用于制动机故障诊断提供了理论基础。初始参数影响HMM的训练和测试效果，K-means算法作为一种简单、高效的聚类算法，可以对模型参数进行快速初始化。特征集对分类器的性能有较大影响，由于制动机风压信号具有非线性[8]特征，故采用核主成分分析(KPCA)对提取的多维特征行约减，去除冗余信息，获得信息主要成分。

鉴于此，本文提出KPCA和优化HMM相结合的方法，采用大秦铁路货车线路实测数据进行验证，并与全特征集HMM和KPCA+HMM以及其它诊断模型进行比较，验证所提方法的有效性。

2 核主成分分析

核主成分分析法利用非线性映射将数据从原始空间映射到高维空间中，然后对其进行主成分分析。其中，核函数及参数决定了原始数据在高维空间的分布，间接决定了KPCA的输出主元成分，故核函数及参数选择对KPCA效果影响较大。

为简化计算，本文选用高斯径向基核函数(RBF)

(1)

式中，σ是宽度参数。在使用核函数进行KPCA分析时，较小的σ会引起过渡拟合，降低分类的泛化性能；而较大的σ会把核函数简化为一个常函数，导致其变成平凡分类器[9]。因此，本文对σ的选择引入类内类间距离，并定义

J=argmax(SB/SW)

(2)

式中，SB是特征集的类间距离，SW是各个特征的类内距离。使得选取的核参数对应的特征类间距最大且类内距最小。

3 优化隐马尔可夫模型

3.1 隐马尔可夫模型

HMM为双随机模型，即状态转换和各状态下的观测值都服从随机过程。根据观测值离散或连续，分为离散HMM和连续HMM。本文采用连续HMM，其描述为[10]：

1) 模型的状态数目N。记N个状态为S1，S2，…，S3，t时刻模型对应的状态为qt，qt∈{S1，S2，…，SN}。

2) 模型每个状态对应的观测值数目M。将观测值记为V1，V2，…，VM，t时刻观测值为Ot，则ot∈{V1，V2，…，VM}。

3) 初始状态矢量π

π={πi}，πi=P(q1=Si) (1≤i≤N)

(3)

4) 状态转移矩阵A

A=(αi，j)，αi，j=P(qt+1=Sj|qt=Si)

(4)

5) 观测值概率密度函数

(5)

一般采用高斯混合模型来表示观测值概率密度函数。其中Mj为Sj状态下单高斯数；ωj，m、μj，m和δj，m分别为Sj状态下第m个单高斯的权重、均值和协方差。

3.2 K-means优化初始模型

HMM训练采用Baum＿welch算法，该算法基于递归思想进行参数估计，寻找最优的模型参数是一个泛函极值问题，因此模型训练和初始参数有一定关系。模型初始参数可以随机化初始，但对其进行估计是有益的，其中观测值概率分布对模型性能影响更大[11]。

本文采用K-means聚类算法对观测值概率分布进行初始估计。K-means算法利用相似性的欧氏距离计算来对样本进行分类，其目标是使各类样本到对应聚类中心距离的总和最小，即类内离散度之和最小。将其设为聚类测度函数，计算公式如下

(6)

式中，Zk为第k个聚类的中心，Ci为第i个分类的集合，k为需要分类的类别数。E反映了样本围绕各聚类中心的紧密度，E越小分类样本分类效果越好。

利用K-means聚类算法优化模型的流程如下：

步骤2：随机挑选个K样本作为初始的聚类中心centeri，1≤i≤K。

步骤3：计算每个样本与各聚类中心的欧氏距离，并按照最小欧氏距离将其划入所对应的类，类中样本量记为numi，1≤i≤K。

步骤4：重新计算各个类中所有样本的平均值，并将其作为更新后的聚类中心centeri。并根据式(6)计算聚类测度函数值Ei，1≤i≤t。

步骤5：循环步骤3和步骤4，得到更新后Ei+1，并计算Ei-Ei+1，判断其与收敛精度Δ的关系，如果小于等于Δ，则退出循环。

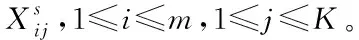
则观测值概率密度函数bj(Ot)的初始参数估计如下

μj，m=centeri(1≤i≤K)

(7)

(8)

(9)

4 基于KPCA和优化HMM的制动系统故障诊断

基于KPCA和优化HMM的制动系统故障诊断的过程如图1，具体步骤如下：

步骤1：对训练集和测试集数据分别进行多维特征提取。

步骤2：计算高斯核函数的最优参数，并利用KPCA对训练集和测试集数据进行降维，得到新的训练集和测试集数据。

步骤3：在训练集数据上，利用K-means聚类算法完成HMM的初始参数优化选择。

步骤4：对训练集不同状态下的样本数据分别训练HMM，并保存到模型库中。本文在制动系统5种状态下，分别训练HMM模型，即λi，1≤i≤L，L=5。

步骤5：将测试集样本送入HMM模型库中，分别计算每个测试样本在不同模型下的似然概率P(O|λi)，其中概率最大的模型就是测试样本对应的状态，即

(10)

图1 制动系统故障诊断流程图

4.1 实验介绍

本文研究的对象为货车空气制动机风压数据，通过对大秦线210辆编组的C80B(H)试验车加装车载监测装置，利用EPCOS(爱普科斯)C82系列空气压力传感器采集货车在线运行过程中多通道风压数据，从而实现制动系统状态监测。如图2所示，空气制动机风压采集点包括列车管、副风缸、制动缸上游、制动缸下游。

图2 压力采集实物图

结合列车行车故障统计表，对试验数据进行统计分析，共得到制动机5种状态数据，每种状态各50组，包括空车正常制动、重车正常制动、缓解不良故障、自然缓解故障、制动缸漏泄故障。图3为制动机5种状态的一组数据展示。其中缓解不良是指列车管充气缓解时，制动缸不缓解或缓解很慢，可能导致货车抱闸运行；自然缓解是指没有缓解操作时，制动缸自行发生缓解作用，可能会导致列车失去制动力而引发事故；制动缸漏泄是指车辆制动保压时，制动缸下游压力持续下降时间>1min，当压力下降到30±10kPa后停止下降。

图3 各种制动状态风压信号图

4.2 特征提取和约减

空气制动机风压信号为多通道时序数据，存在周期性、随机性等动态特性，对其时域和频域基本特征进行提取。时域特征包括均值、方根幅值、标准差、均方根值、峰峰值、偏度、峭度、波形指标、峰值指标、脉冲指标、裕度指标；频域特征包括平均频率、中心频率、均方根频率、标准差频率、频率峭度。

制动机在制动过程中内部气路管道压力存在阶跃变化的过程，而小波分析对这类边缘信号有很好的处理效果，不仅有滤波作用，并且可以从阶跃型信号中提取信号的突变点[12]。故对多通道数据进行小波分析，选取db3对信号进行3层小波包分解，计算各频带的能量谱尺度，选取前三作为特征。

空气制动机是一个复杂的耦合系统，各零部件间存在相关性关系，故对多通道风压数据提取相关性特征。本文计算皮尔森相关系数作为特征，其计算公式

(11)

将采集到的250组数据，各状态下随机选取60%数据作为训练集，其余作为测试集。对各组数据特征提取后，采用KPCA进行特征降维，核函数参数σ的选择如式(2)所述，以1为步长，对σ∈[1，200]内的 200个点进行计算，选取J最大时所对应的核参数。对训练集和测试集数据进行KPCA，分别选取最优的σ1=12，σ2=11。并设置主元贡献率≥85%，保留前三阶主元进行分析。图4(a)和(b)分别是训练集和测试集降维后的前三主元的分布。从图中可以看出经过KPCA处理后的特征可以有效分辨空气制动机5种不同状态的数据，可用于空气制动机的故障诊断。

图4 KPCA后特征结果

4.3 HMM模型建立

HMM参数选择：高斯元数目M=2，训练迭代次数为10。对马尔可夫链和协方差矩阵的类型采用网格搜索法的方式，在训练集数据上采取5折交叉验证，以模型平均诊断准确率作为参数选择的标准。确定马尔可夫链为左右型且状态数为5，协方差矩阵为对角型。

利用K-means算法对HMM的初始参数进行优化选择，然后进行模型训练。设置聚类中心数K=M，聚类迭代次数t=10，聚类测度函数的收敛精度Δ=1e-4。图5给出了在迭代过程中，对KPCA后的训练集特征进行聚类时聚类测度函数值的变化曲线，体现了各类样本中最佳个体类内离散度之和的变化趋势。从图中可以看出，各类样本中最佳个体类内离散度下降明显，且在迭代步数内满足收敛精度要求。

图5 聚类测度函数值收敛曲线图

在模型训练和测试阶段，为验证本文所提方法的有效性，将该方法与全特征HMM和KPCA+未优化HMM进行对比。图6为3种方法训练收敛曲线图，纵坐标为训练迭代过程中的各模型平均似然概率。从图中可以看出，KPCA+优化HMM的方法大大提高了模型的训练效率，在训练的第3步可以达到收敛精度，KPCA+HMM收敛速度次之，全特征HMM收敛速度最慢。

图6 模型训练过程收敛曲线

4.4 诊断结果

图7为全特征集训练HMM的诊断结果，图8为KPCA+未优化HMM诊断结果，图9为KPCA+优化HMM诊断结果，其中横坐标1-20、21-40、41-60、61-80、81-100分别表示状态为空车正常制动、重车正常制动、缓解不良、自然缓解、制动缸漏泄的测试样本，纵坐标对应的是测试样本在不同模型中的似然概率。由图7可知，空车正常制动的样本全都能被正确诊断，无误判样本，重车正常制动样本(编号21-40)除编号40外，其余样本都在模型下取得最大对数似然概率，因此判断这些样本为重车正常制动状态，而编号40的样本则出现了误分。同理，缓解不良样本出现2次误分(编号50和55)，自然缓解样本出现4次误分(编号62、67、72和73)，制动缸漏泄样本出现3次误分(编号88、95和98)。由图8可知，空车正常制动、重车正常制动的样本全都被正确诊断，缓解不良样本出现1次误分(编号47)，自然缓解样本出现1次误分(编号72)，制动缸漏泄样本出现2次误分(编号88、95)。由图9可知，除了缓解不良样本出现1次误分(编号47)和制动缸漏泄样本出现1例误分(编号88)外，其它样本都被正确诊断。诊断结果见表1。

由表1可知，诊断空车正常制动时，三种方法诊断率相同，对其它制动状态诊断时，KPCA+优化HMM较KPCA+HMM及全特征HMM，获得了更好的诊断效果。这是由于KPCA对特征集进行约减，获得特征主要成分，提高了模型的收敛速度，并且利用K-means算法优化初始模型参数，降低了训练难度，提高了模型的训练效率，使得诊断准确率有了一定的提高。

为了对比其它诊断模型的分类效果，分别设计基于支持向量机(SVM)和随机森林(RF)的故障分类器。SVM选择RBF核函数，c=0.435，gamma=0.25。随机森林参数：分类器个数为10，决策树的最大深度为5，叶子节点的最小样本数为2。其诊断结果如表2所示。RF由于采用了集成弱分类器的学习策略，相比没有经过集成策略的单分类器模型SVM，泛化能力更强，诊断准确率更高。但是相较于HMM这种可以对时间序列建模的模型，HMM更能反映出时间序列过程中的状态指标变化，对长时间序列比如制动数据有更好的故障识别效果。

图7 全特征HMM诊断结果

图8 KPCA+HMM诊断结果

图9 KPCA+优化HMM诊断结果

表1 诊断结果比较

表2 其它模型诊断结果

5 结论

根据铁路货车制动系统故障诊断特点，提出了采用KPCA和优化HMM相结合的方法。该方法利用KPCA对特征参数进行约减，去除其中大量的冗余信息，降低了模型的复杂程度，并利用K-means聚类算法优化模型初始参数，提高了HMM训练和测试的效率。结果表明，基于KPCA和优化HMM的故障诊断方法能很好地表征空气制动机的故障状态，具有很高的诊断精度，为铁路货车制动系统故障诊断提供了一种切实可行的方法，具有一定的参考价值。