基于历史发生原理的高中数学学科育人教学实践探索——以“球的体积”为例

朱亚萍，马 晟

(黄冈师范学院 数学与统计学院，湖北 黄冈 438000)

2014年，《教育部关于全面深化改革课程落实立德树人根本任务的意见》明确指出：要充分发挥人文学科独特的育人优势，进一步提升数学、科学、技术等课程的育人价值[1]。《普通高中数学课程标准(2017年版)》(以下简称《标准(2017年版)》)中提倡高中数学课程应以学生发展为本，落实立德树人根本任务，培育科学精神和创新意识，提升数学学科核心素养，同时注重数学文化的渗透[2]，不仅如此，修订版的课程标准也强调应加强以育人为导向的课程建设[3]。2017年教育部印发的《中小学德育工作指南》为中小学德育工作提出了具体的实施途径和要求，将“课程育人”作为重要的实施途径之一，其中数学等课程要加强对学生科学精神、方法、态度、探究能力和逻辑思维能力的培养，促进学生树立勇于创新、求真务实的思想品质[4]。中共中央国务院印发的《中国教育现代化2035》指出：为全面落实立德树人根本任务，发展中国特色世界先进水平的优质教育，应广泛开展理想信念教育，不断提高学生的文化素养，强化实践能力、创新能力的培养[5]。在教育部印发的《完善中华优秀传统文化教育指导纲要》中也要求：加强中华优秀传统文化教育，发挥课堂教学的主渠道作用，在高中阶段以增强学生对文化的理性认识为重点，引导学生感悟文化的精神内涵，数学课程应结合教学环节渗透文化[6]。上述文件表明了国家对学科育人实践的高度重视，对此，很多学者也提出了自己看法。有学者认为践行学科育人是落实立德树人的最佳途径[7]，文化浸润课堂是彰显学科育人价值的重要方式。而学科育人价值的挖掘则需要透过知识的表层，去追寻知识背后的文化意义与价值传承[8]。还有学者认为学科教学中育人价值的挖掘、开发可从教学内容、教学方法、教学工具三个角度考虑[9]。有学者指出让文化浸润课堂，促进学生数学思维的发展从而让深度学习也随之发生，引导学生对文化形成同一性直至增强文化自信是学科育人功能的实践诉求之一[8]。基于这种关系，数学文化融入数学教学在顺应《标准(2017年版)》的同时也更好的满足了学科育人价值的实践诉求。关于以文化育人为导向的学科育人理论研究为实践指明了方向，但如何将教学理论成功转化为教育实践才是学科教学论走向实践应用状态的标志[10]。

球的体积是高中数学“立体几何初步”中的重要教学内容，要求教师以这部分教学内容为载体，让学生体会直观感知、操作确认、推理论证、度量计算研究几何对象的一般过程，并循序渐进地安排推理训练，发展学生的逻辑推理素养。普通高中数学人教版教材中是根据球的表面积公式利用极限的思想推导出球的体积公式，在该教学内容结束后的“探究与发现”中介绍了利用祖暅原理探究几何体体积的公式。但是，教材中没有提到了如何用祖暅原理来探究球的体积公式。这种编排形式，为教师在备课、备教材时留有很大的思考、创造空间。而一项关于高中数学立体几何相关问题的调查研究表明：高中数学课堂中立体几何的教学存在着对公式直接灌输、教学方式陈旧等现状从而导致学生在学习过程中缺乏思考空间、学习动机匮乏、强行记忆知识点的现象[11]。由此可见，数学史融入数学教学的趋势方兴未艾，实际教学中存在的问题并不少。基于此，为贯彻《标准(2017年版)》的重要理念，本文以高中数学中“球的体积”为例，以“历史发生原理”为理论基础，以问题串驱动为导向，以发生教学法为策略，将知识的历史发生顺序合理的融入到教学中，在提升数学核心素养的同时最大程度的彰显数学学科独有的育人价值。

1 历史发生原理与“球的体积”的历史发展

“历史发生原理”源自于德国生物学家赫尔克提出的生物发生律，即“个体发育史重蹈种族发展史”[12]。后来将此原理应用于教育学中即“个体知识的发生过程遵循人类知识的发生过程”[13]，它是数学史融入数学教学的理论之一。学科育人作为教学的核心任务[14]，教师应有意识的发展学科教学知识，创造性的运用数学史进行教学设计才能使历史发生原理实现其应有的教学功能[15]。有学者指出，教师能将理论在特定的情境中应用于实践，是教师专业化发展的前提和基础，是教学理论走向实践化的中介，这也是教学工程化的实质要求，即教师在教学工作中运用已有的教学理念进行教学实践[10]。历史发生原理应用于教学实践的体现是发生教学法[16]，该方法不仅为促进数学史与数学教育之间的融合搭建了有效地桥梁，也是数学史融入数学教学提高学生数学学业成绩的重要方式[17]。发生教学法应用于教学时应遵循以下几个步骤：1)教师在备课时应熟知教学内容对应主题历史的发展过程；2)深入理解主题历史发展的关键环节，从而挖掘每个发展环节的动因以及数学家在解决问题时所遇到的困难和认知障碍；3)在特定的现代情境中重新构造这个发展环节的关键步骤，在此基础上引入新的概念；4)根据重构的步骤设计出由易到难的问题串从而推动课堂教学的发展[18]。

本文正是根据历史中关于这部分内容的发展脉络，在教学前通过充分了解授课对象的原有认知水平，运用发生教学法对“球的体积”求法的历史发生顺序进行排列，构造出符合学生实际情况的教学情境，激发学生的学习兴趣，帮助学生跨越学习的认知障碍点。同时，让学生在先贤的智慧中感悟数学文化的同时发挥课堂的育人价值，推动课堂的发展迈向高潮，用数学思想和理性精神滋养学生[20]。

2 基于历史发生原理实现学科育人价值的教学分析

学生在学习“球的体积”这一教学内容之前已学会了柱体、锥体、台体等基本几何体的表面积与体积，此教学内容将为学生的直观想象、逻辑推理素养的发展提供有效途径。为了让文化浸润课堂，充分彰显数学学科育人价值，本节教学内容选用我国古代关于球体积的探索路径，将球体积发生的历史进行重构，引发学习的认知冲突。在深入学习知识的同时，选取最佳时机将数学文化融入教学，充分利用文化的育人功能。因此本节教学内容的重点是利用祖暅原理推导球的体积公式。

本节课的授课对象为高中一年级的学生，部分学生了解球的体积公式，但没有经历公式的推导过程。授课对象具有一定的抽象能力但逻辑推理能力有待提升。高一的学生思维活跃、对知识的发展过程具有较强的好奇心，并且已有大量球体的认知。因此本节课的难点为如何利用祖暅原理的使用条件构造出与球体成比例的几何体从而证明球的体积公式。

为了顺利完成本节内容的教学目标(如图1所示)，本文以建构主义为核心，在问题驱动的“启发式+探究式”的教学法基础之上结合发生教学法，根据学生已有的认知基础建构新知。帮助学生从生活实例到抽象球体、从感性认识到理性思考的过度。

图1 教学目标

3 基于历史发生原理的学科育人教学过程体现

3.1 课前研学 发展科学精神和创新意识

根据学生的基本情况和原有认知水平，大部分学生都具备一定的关于球体知识的生活经验。基于此，课前布置研学方案：“探究生活中球体的体积”后由各小组推荐的发言人交流展示研学成果。一部分小组利用“排水法”(如图2所示)，将球丢进有水的圆柱形杯子中，通过观察、比较水面高度的变化求出了球的体积。另一部分小组利用Excel表格进行函数拟合找到了球的体积公式的函数模型(如图3所示)。

图2 排水法”求体积

图3 体积公式的函数模型

学生展示：在商店里通过商品详情收集了一些生活中球体的半径、直径以及体积的具体数值，以半径为横轴、体积为纵轴绘制散点图后进行函数拟合，利用多种函数进行拟合，最后发现，幂函数的拟合度达到了1。由此学生认为球的体积公式应该是一个幂函数模型。

根据学生代表发言情况，深入剖析问题所在：用“排水法”求球的体积是可行的，但是关于这一几何体体积公式的求法还有待探讨。通过分析数据，建立球体积公式的模型存在误差。根据此时学生对球体积公式的认知障碍，设计生活化的数学问题情境，激发原有认知水平。

教师出示问题情境：许多人喜欢喝加冰块的饮料，假设你要点一杯冰咖啡，服务员给你提供两种加冰块的选择：A.边长3 cm 方形冰块5个；B.半径2 cm 球形冰块5个；哪一种选择喝到的咖啡多？

通过课前的研学方案，让学生在自主研学中提升追求真理的科学精神和创新意识，培养学生在解决问题时敢于质疑、动手操作、勇于创新、自主思考的好习惯，为本节课新知识的学习做好铺垫。问题情境的求解需要用到球的体积公式，由此引出课题。

3.2 实验探究 提升学科核心素养

为了避免灌输式教学，使深度学习在数学课堂中滋生，实施发展性教学，充分发挥课堂的育人功能[21]，球的体积公式采用“先猜后证”的方式推导证明。基于学生对圆柱体、圆锥体的学习基础，设置问题情境引导学生猜想并验证，以动手操作的形式学习知识，为后续的理论证明作铺垫。

教师引导学生联想并猜测球体与圆柱体和圆锥体之间的联系。由于学生对圆柱体、圆锥体已具备基本的几何直观，部分学生会猜测“半球”。通过图形外观来看，半球是介于圆柱和圆锥之间的一种几何体。根据球的几何性质教师向学生提问：假设圆柱的体积为V，这时圆锥的体积时多少？

此时学生根据教师的问题猜想：这个半球的体积是多少呢？学生的想法各不一致，但大部分学生此时能想到可以通过球的体积来求半球的体积。教师引导学生根据学具(同底高都为R的半球、圆柱、圆锥)验证半球的体积与圆柱和圆锥之间的关系。

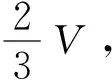
从实际问题出发，引导学生应用已有的知识和经验探索未知的世界，体会直观感知、操作确认的一般几何问题的研究过程，引导学生“先猜后证”，逐步将教学推向课堂发展的关键环节，发展直观想象的数学素养，提升解决实际问题的能力。

3.3 重塑历史 浸润数学文化

苏联教育家赞可夫在《教学与发展》中提出了发展性教学观的教学原则，即“教学应使所有学生都获得一般发展”，他主张教学应打破书本知识传授的局限性，让教学走在发展的前面。据此，通过将知识的历史发生顺序进行重构，设置情境引发学生的认知冲突，引导学生跨越认知的障碍点，提升学科教学的发展性，让学生在感悟文化的过程中发展思维品质，引发学生深度学习。在教学时融入古代数学家在解决实际问题过程中所遇到的问题、困难，让学生了解知识的历史发生过程，让文化浸润课堂，渗透我国古人在探究过程中的科学精神与态度，凸显学科育人的实践诉求。

教师引领学生沿着历史的足迹探寻我国古人是如何对球的体积公式进行探究、论证的(如图4所示)。关于球的体积的求法最早起源于《九章算术》中的“开立圆术”，刘徽对《九章算术》进行注解时发现其中有一定的局限性，于是对其进行了整改，但是在他的有生之年并没有找到“牟合方盖”这个几何体体积的求法。最后祖冲之和他的儿子祖暅延续了刘徽的思路提出了祖暅原理使得球的体积公式得以证明。意大利数学家提出的 “卡瓦列里原理”与祖暅原理的本质是相同的，但是祖暅原理的发现早于卡瓦列里原理1000多年。由此可见，我国古人对数学的发展作出了卓越的贡献。

图4 球体积的历史发生顺序

在介绍球体积的历史发生顺序后教师出示祖暅原理并提问，你能从图中(如图5所示)总结出祖暅原理的使用条件吗？此问题为球的体积公式的证明提供理论导向。教师在讲解祖暅原理的同时利用动态软件呈现S1、S2、S3之间的关系，让学生从直观上感知原理的合理性。学生通过观察动态图总结使用祖暅原理的使用条件：两个(或以上)几何体等高；同高处的横截面积相等。

图5 三种几何体体积的比较

学生通过观察动态图总结使用祖暅原理的使用条件：如果两个(或以上)几何体等高，并且同高处的横截面积相等，那么这两个(或以上)几何体的体积相等。

从理论层面证明球体积公式为教学的关键环节，教师出示问题：根据祖暅原理的使用条件，如何才能构造出两个符合祖暅原理的几何体来证明球的体积呢？通过这一问题引导学生从理论层面探索新知发现球体积证明的发展的关键之处在于构造两个符合祖暅原理的几何体，让学生感受数学家在解决问题时所遇到的困惑以及数学家们突破问题疑难点的关键过程，由此在教师的引导下将球体积的证明这一问题化繁为简。

此时学生思考：如何构造几何体呢？教师追问：用平行于底面的平面去截它们，它们的截面面积相等吗？学生根据图形可以直观的感受这两个几何体的截面面积是不相等的。教师再次追问：怎样才能让它们满足祖暅原理的条件呢？学生通过观察并思考尝试着把挖去圆锥的圆柱倒过来试试。

为了验证学生的想法，通过数学动态软件来验证这两个几何体是否符合祖暅原理的要求，用平行于这两个平面的任意平面去截这两个几何体，观察它们截面面积的变化情况，可以看出它们任何时候都是相等的(如图6所示)。这样就可以借助这两个几何体对球的体积公式进行推理论证。

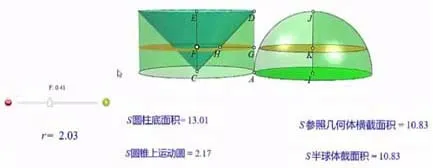
图6 祖暅原理示意图

教师出示问题：用平行于底面的截面去截它们，截面面积是否相等呢？学生根据图中给出的已知条件以及图中所隐藏的几何关系，计算S1和S2的面积(如图7所示)。

图7 截面相等的几何体

让学生感受数学家发现问题，突破问题疑难点，解决问题的关键过程，深入挖掘历史发展的动因，引导学生从理论层面探索新知，渗透转化的数学思想。发扬敢于质疑、勇于探索的科学精神与态度，引入数学文化，由此增强学生的民族自豪感和文化自信。

3.4 学以致用 提升求真务实的思想品质

学生通过动手操作、理论推导证明了球体积公式之后，对球体积这一教学内容不仅仅是对公式的单一记忆，对于公式的历史来源也有了更深刻的理解。基于此，引导学生自行解决学习新知识之前提出的实际问题，强化知识的应用。让学生交流总结本节课的所学及感悟，升华教学内容，凸显育人价值。教师引导学生解决加冰饮料的问题情境，感受利用新知解决问题的喜悦感。

教师提问并引导学生总结反思本节课所学知识，强化记忆，交流、总结思想，谈谈收获。学生本节课的学习感悟是：本节课学习了球的体积公式，并用祖暅原理证明了该公式，深刻认识到我国历史文化的悠久，感受了我国古人对数学的钻研精神，由此增强了我们的民族自信和文化自信。还有学生谈到：本节课我们在利用祖暅原理对求体积进行推理论证是运用了转化与化归的思想。最后，教师根据学生的交流做总结并布置课后作业。为了使本节课所学习的知识在课后得到更好的巩固与提升，本节课的课后作业是：假设每一个小石子为球形，小石子的半径为3 cm，一共投入了18个石子，瓶子里物体的总体积增加了多少？

强化新知识的应用，检验学生对本节课内容的理解和运用程度。通过梳理本节课的知识要点以及数学思想方法，进一步巩固本节课的知识。总结本节课所学知识的历史发生过程，让学生感受我国深厚的历史文化底蕴，提升学生求真务实的思想品质，发挥学科育人价值。

4 课堂实践与反思

本文以历史发生原理为基础，运用历史发生法，对“球的体积”这一教学内容进行教学设计。研究者于2021年5月在黄冈师范学院第六届教育硕士微课大赛中进行了模拟课堂教学并有幸荣获二等奖，此后在麻城二中经课堂实践后通过与专家评委交流总结了以下几点：在教学过程中以学生的已有认知为出发点，创造性的利用教材和知识发生的顺序能让学生达到良好的学习效果；运用发生教学法深入挖掘了历史知识发展环节的关键步骤，使得学生在遇到新问题时积极踊跃探索，学生的科学精神和创新意识得到了发展，直观想象、逻辑推理的素养获得了培育；在重塑历史，浸润历史文化这一教学环节，重构知识的发展顺序，构建以人文为导向的课堂，彰显数学课程独有的学科育人价值；在教学过程中构建新途径，给予学生更多的思考、探究空间，学生的探究问题意识得到了逐步提升。但也有不足之处，在构造几何体证明球的体积公式时在教师的反复引导下学生顺利的构造出证明球体积公式的两个几何体，如果教师能够放手让学生大胆尝试自主探究构造，可能会给予学生更多的创造空间。