基于模态分解的轴对称超声速射流啸声产生位置数值分析1)

李虎 罗勇 韩帅斌 王益民 武从海 刘旭亮

(中国空气动力研究与发展中心,空气动力学国家重点实验室,四川绵阳 621000)

(中国空气动力研究与发展中心,计算空气动力研究所,四川绵阳 621000)

引言

超声速射流在航空航天飞行器的推进系统中广泛存在和应用.由于喷管构型的限制,大多数超声速射流是不完全膨胀的,其势核中的激波栅格结构与剪切层中的湍流拟序结构的相互作用会产生强烈的激波噪声.啸声是激波噪声频谱上的离散频率声模态,主要向上游传播,声压级可高达160 dB.高强度的啸声不仅会造成严重的环境噪声污染,还会使飞行器控制舵面、尾喷管结构部件产生声疲劳、甚至断裂,危及飞行安全,是发展军用/民用超声速飞行器急需解决的重要问题之一.

Powell[1]首次发现射流啸声,并将其产生机制解释为非线性的自激声反馈环机制.自此先驱性工作开始,普遍认为啸声反馈环包含4 种关键机制[2-4]:剪切层中的拟序结构的增长、激波栅格结构和拟序结构的相互作用、声反馈和喷管唇口附近的感受性过程.此外,Powell[1]还发现啸声频率在随完全膨胀射流马赫数(Mj)变化时存在模态跳跃行为.在圆射流中,Powell 确认了A、B、C、D 4 种啸声模态.Merle[5-6]发现A 模态可分为A1和A2两个亚模态.Davies 和Oldfield[7]和Powell等[8]发现圆射流中的啸声模态与射流的内禀不稳定性直接相关,并且确认A1和A2模态是轴对称模态,B 和D 模态是摆动模态,C 模态是螺旋模态.Ponton 和Seiner[9]发现摆动模态是由两个同量级的反向螺旋模态叠加而成.Clem等[10]在完全膨胀射流马赫数为1.0 ＜Mj＜1.7 的圆形收缩喷管实验还捕捉到了啸声B′模态、E模态和F 模态.对于低马赫数超声速射流,轴对称模态是主导啸声模态[11-12].Ponton等[13-14]在声速喷管欠膨胀射流实验中记录了啸声A0模态,Li 和Gao[15]在轴对称URANS 模拟中也捕捉到了该模态.Gao 和Li[16]根据他们提出的新的啸声波长(频率)预测公式,提出Ponton等[13-14]在实验中测量到的两种A0模态可以归类为A1和A2模态,给出了啸声A0模态的一种新解释.

理解啸声的产生机制,需要对啸声反馈环的各个环节进行深入研究.作为环节之一,射流剪切层内拟序结构与势核内激波栅格结构的相互作用涉及啸声声波的产生过程和产生位置.为了解释激波/拟序结构相互作用如何产生啸声声波,基于模型问题,即剪切层与单个孤立的压缩波-膨胀波结构单元的相互作用,Manning[17]提出了“激波泄漏(shock leakage)”机制.Suzuki 和Lele[18]进一步发现局部涡量对激波起到屏障作用,激波会在剪切层内旋涡之间的鞍点也就是局部涡量较弱的区域泄漏,也就是说,激波泄漏和关联啸声的产生只能发生在射流剪切层大尺度湍流结构充分发展并且具有明晰的鞍点的区域.自此之后,激波泄漏机制受到了越来越多的关注,并逐渐被数值[19]和实验[20-21]所证实.

激波泄漏机制虽然指出了剪切层中的旋涡鞍点是影响射流啸声产生关键结构,但其还有不足:未能给出每种模态啸声的精确产生位置.为了定量的理解啸声反馈环,精准定位每种模态啸声的有效声源位置至关重要.Powell等[8]基于纹影发现啸声A1、A2和B 模态的声波是在喷管下游5 倍直径处的区域辐射,而啸声C 模态的声波辐射中心位于喷管下游六倍直径的区域.Umeda 和Ishii[22]利用瞬时纹影发现螺旋C 模态的主控声源位于第3 个激波栅格结构的尾缘.Edginton-Mitchell等[23]采用高分辨率平面PIV 也研究了螺旋C 模态,认为啸声声波可能是在第2、第3 和第4 个激波反射点处,且拟序涡量经历最大脉动时产生.Gao 和Li[16]基于数值分析认为前5 个激波栅格是啸声A1,A2,B 和C 模态的有效声源区,并且主控声波是在第2 和第4 个激波栅格之间产生.Panda[24]则通过啸声同相压力脉动的近场映射发现啸声A2模态的声波是从第3 和第4 个激波尖梢之间某个位置辐射.Shariff 和Manning[25]发现与A1模态相关的激波泄漏和噪声辐射是在第3 和第4 个激波栅格的激波尖梢处.Edgington-Mitchell等[21]发现在第3 和第4 个激波栅格结构的激波尖梢处会产生与A1模态相关的噪声辐射.基于近场声测量和时间分辨的纹影成像,Mercier等[26-27]认为轴对称啸声A1模态和A2模态都是在第4 个激波栅格的尾缘(激波尖梢)处产生,而B 模态是在第3 或第4 个激波尖梢处产生,具体取决于马赫数.Li等[28-29]通过数值模拟研究发现啸声螺旋C 模态的有效声源位于第4 个激波栅格,A1和A2模态的有效声源位于第4 个激波栅格下游,B 模态的有效声源位于第3 个激波栅格下游.

精确定位啸声的声源位置是定量理解啸声反馈环和预测啸声频率的一个关键所在[26].然而,截止目前,关于每种啸声模态究竟是单声源还是多声源,以及各模态啸声具体的声源位置还存在一定的争议.而且,同一类型啸声模态的产生位置还可能与具体的射流马赫数相关.现有研究涉及的射流马赫数范围还比较有限,需要针对不同的射流马赫数开展研究.本文采用高精度数值方法直接求解轴对称可压缩Navier-Stokes 方程,数值模拟了射流马赫数为1.10 和1.15 的圆形声速喷管欠膨胀超声速冷射流,得到了A1和A2两种轴对称模态啸声.基于精细的非定常流场数据,通过傅里叶模态分解、本征模态分解和动态模态分解,研究了啸声关联流动结构的空间演化,定位了两种轴对称模态啸声的有效声源位置.

1 物理模型和数值模拟方法

1.1 控制方程

对于低射流马赫数欠膨胀超声速射流,啸声的主导模态是轴对称模态,在产生啸声的流动范围内,剪切层内的大尺度不稳定波或拟序结构也呈轴对称形态,三维效应并不明显.因而,控制方程采用轴对称可压缩Navier-Stokes (N-S)方程,该方程是从柱坐标系下的三维可压缩N-S 方程退化而来.

无量纲的轴对称可压缩N-S 方程具体形式如下

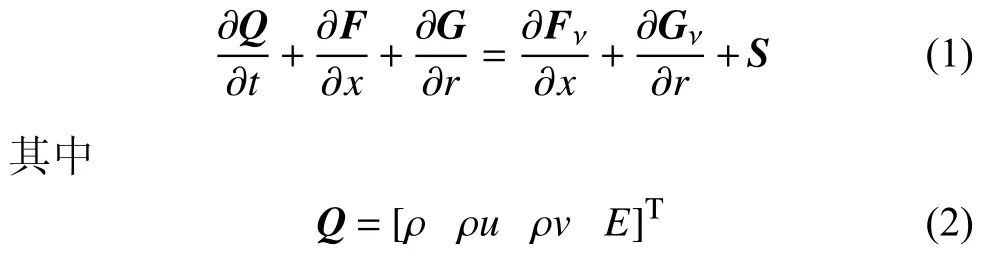
是守恒变量,F和G是x和r方向的无黏通量

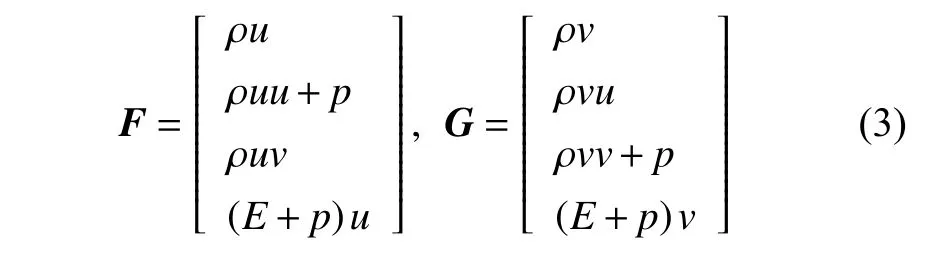
Fv和Gv是x和r方向的黏性通量,即

S是源项,即

E是单位体积总能,即

黏性应力项为

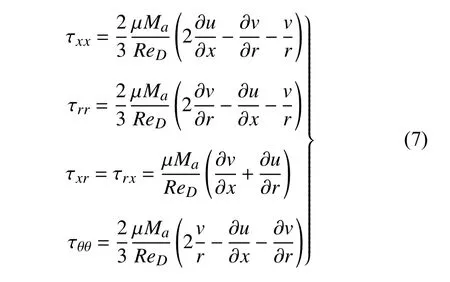
x和r方向的热流率为

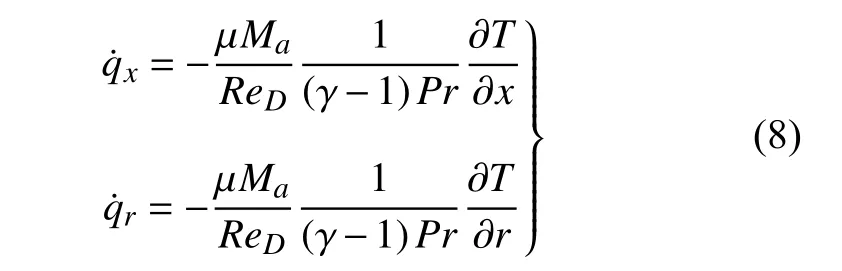
完全气体状态方程和声速表达式如下

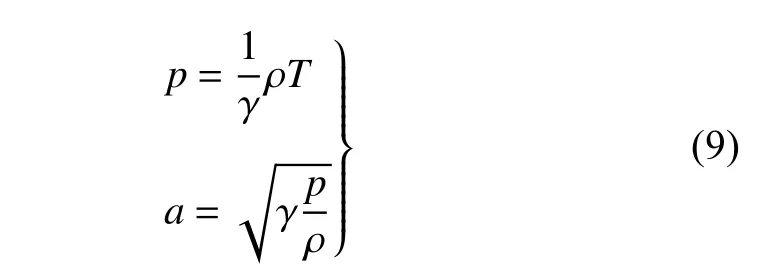
黏性系数根据Sutherland 公式计算

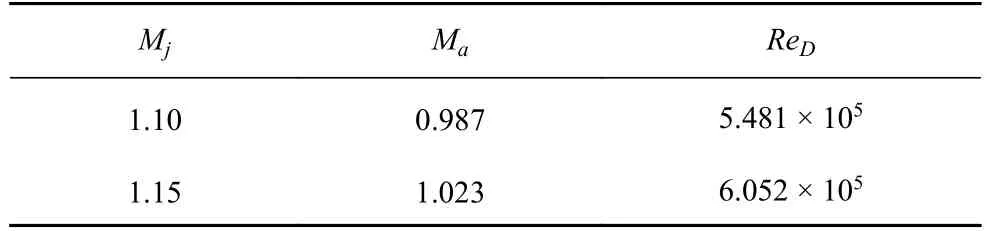
表1 欠膨胀超声速射流的关键流动参数Table 1 The key flow parameters in underexpanded supersonic jet

1.2 数值方法

控制方程的空间对流项离散采用五阶精度的有限差分加权本质无振荡(WENO-JS-5)格式[30],迎风处理采用Van Leer 流通量分裂方法[31];此外,还采用了改善WENO 格式收敛能力的技术[32-33]来消除激波的波后振荡.空间黏性项离散采用6 阶精度的有限差分中心格式,时间导数项离散采用3 阶精度的3 步TVD Runge-Kutta 格式[30].

5阶精度的有限差分WENO-JS-5 格式形式如下:

5点总模板上的数值通量可以表示为3 个3 点子模板上3 阶数值通量的凸组合,即

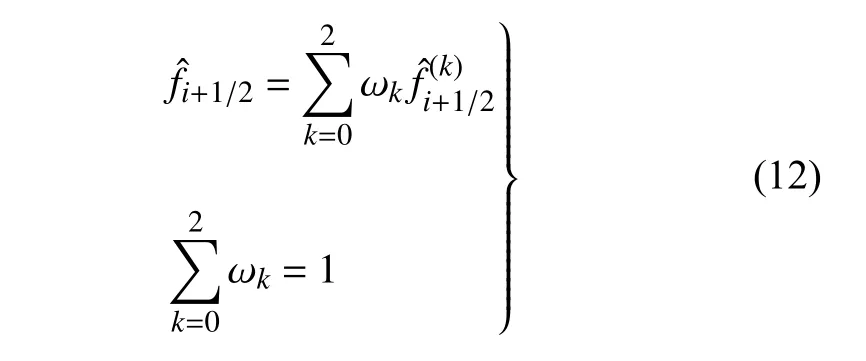
子模板上的数值通量为

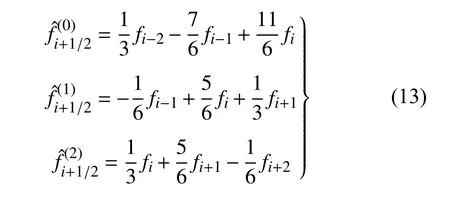
非线性权为

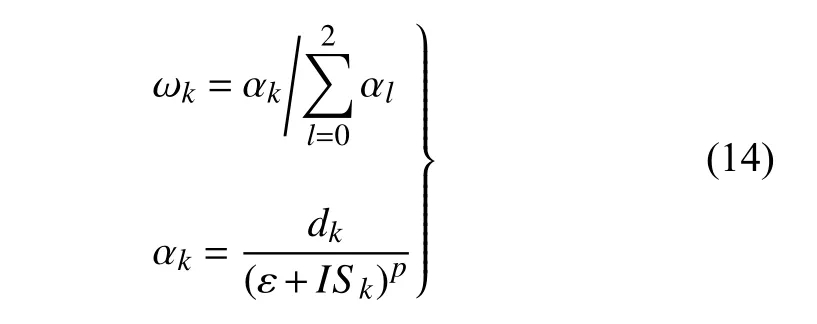
其中,ε=10-6和p=2 .线性权为

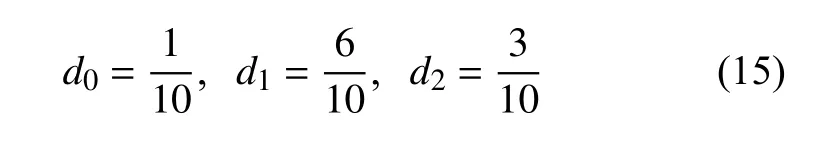
光滑因子为

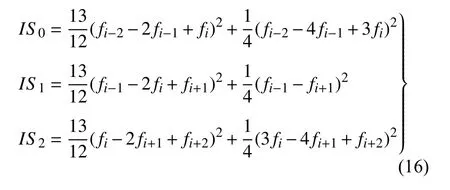
控制方程的对流项和黏性项经过空间离散后,得到一组常微分方程

其中,L(Q) 表示空间离散算子.3 阶精度的3 步TVD Runge-Kutta 格式形式如下

1.3 计算域和初边值条件

计算域和边界条件的设置如图1 所示.在物理域 -2D≤x≤15D和0 ≤r≤6D内,计算网格均匀分布,Δx=Δr=0.02D.在物理域之外,网格开始拉伸以消除反射声波.

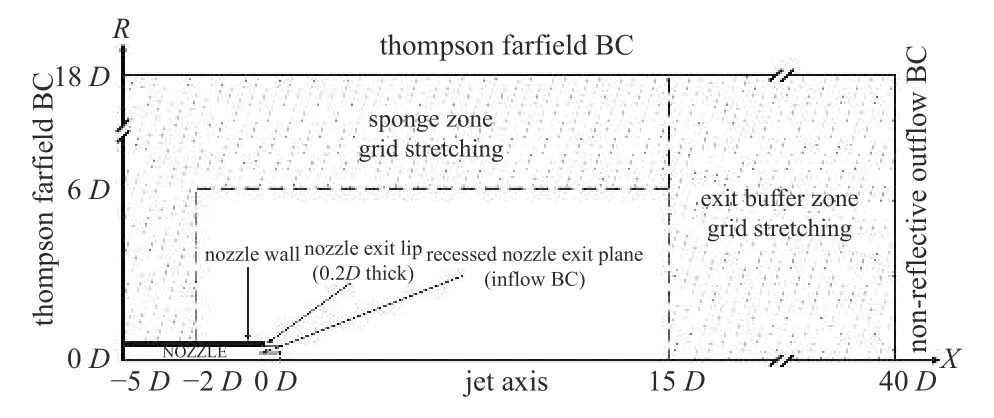
图1 计算域和边界条件示意图Fig.1 The schematic of the computational domain and boundary conditions

计算域的上边界和左边界采用Thompson 的特征远场边界条件[34-35];在下游边界区域,采用无反射出流边界条件[36].在射流轴线上,由控制方程中含“ 1/r”的项所导致的奇性轴问题采用极限法[37]转换成偏导数进行处理.此外,对轴线上的偏导数进行有限差分离散时,计算域也需拓展到的r＜0 的区域,相应的变量通过与r＞0 的区域的镜像关系求得.喷管壁面采用无滑移边界条件.在喷管出口处,入流平面内移6 个网格以便激发出不稳定波,减小对反馈环的数值限制和影响.喷嘴出口处的入流平面为声速平面,无量纲形式的流动变量设置如下[15]

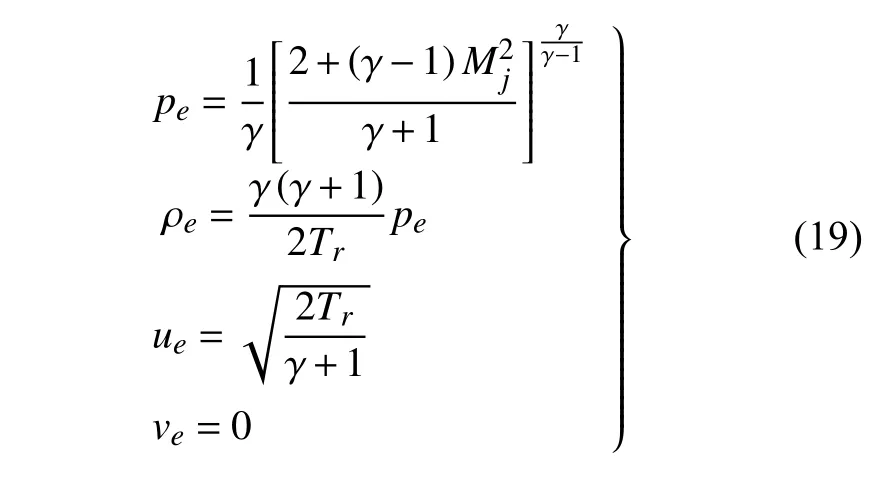
其中,比热比 γ=1.4 ;Tr为储气罐温度,根据冷射流假设,Tr=1 .

需要强调的是,在整个计算过程中,入流条件处并没有添加任何形式的人工扰动.因此,啸声反馈环的产生和维持都不需要任何外部激励.

初始时刻,除了喷管出口处,整个计算域内都设置为环境流动条件

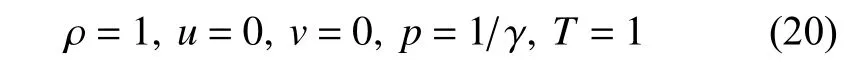
上述参数表示射流由喷管射入周围静止的空气.

为了方便对数值结果进行分析,计算选取固定的无量纲时间步长,具体取值为 Δt=0.002.为了确保时序信号傅里叶分析的精度,计算需要推进大量的时间步,总的无量纲积分时长为T=2500.本文所采用的数值方法、计算程序及针对轴对称超声速射流计算的网格无关性验证见文献[38].

2 数值模拟结果与分析

2.1 激波栅格结构

啸声声波是由射流势核中的激波栅格结构与剪切层中的大尺度拟序结构相互作用产生,因此,准确地模拟激波栅格结构的位置对于定位啸声的有效声源位置至关重要.

图2 是完全膨胀射流马赫数为1.10 和1.15 的欠膨胀超声速射流轴线上的时间平均压力分布.为了验证当前轴对称数值模拟的准确性,将其结果与André等[39-40]的实验结果进行了对比.图中显示,对于前3 个激波栅格,两种状态的数值解都与实验测量值吻合得很好,无论是激波位置还是幅值.对于第4 个激波栅格,数值解的激波幅值与实验测量值有所偏差,但激波位置吻合.在第5 个激波栅格结构之后的区域,数值解与实验测量值差别较大,其原因可能是在此区域轴对称控制方程物理上不再成立.由前文可知,啸声一般是在第5 个激波栅格的上游区域产生,所以这些偏差并不影响后续关于轴对称啸声模态产生位置的分析.

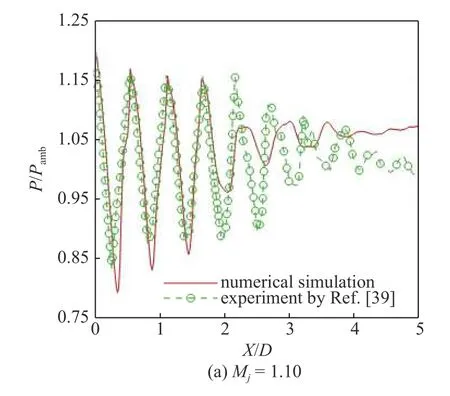
图2 射流轴线上的时间平均压力分布及其与实验结果[39-40]的比较Fig.2 The time-averaged pressure along the jet axis and its comparison with the experimental results[39-40] of screeching jet

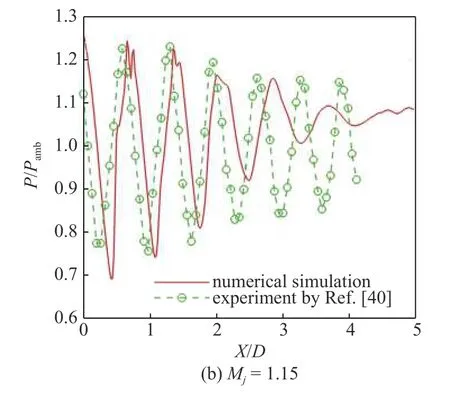
图2 射流轴线上的时间平均压力分布及其与实验结果[39-40]的比较 (续)Fig.2 The time-averaged pressure along the jet axis and its comparison with the experimental results[39-40] of screeching jet (continued)

2.2 啸声的频率与声压级

在喷管唇口壁面上设置压力监测点[0.0D,0.642D],记录该位置处的时序压力信号,采用快速傅里叶变换(单边模式) 进行处理,得到近场噪声频谱信息.图3是Mj=1.10,1.15 这两种状态欠膨胀超声速射流的近场噪声频谱分析结果.图中的横坐标表示频率,单位是 Hz,频带宽度是75 Hz;纵坐标表示声压级,单位是dB.对于Mj=1.10 的欠膨胀超声速射流,有两个尖锐的声压级凸起,分别是轴对称A1模态及其谐频.对于Mj=1.15 的欠膨胀超声速射流,可以识别出3 个有意义的声压级凸起,分别是轴对称A2模态及其第1、第2 谐频.

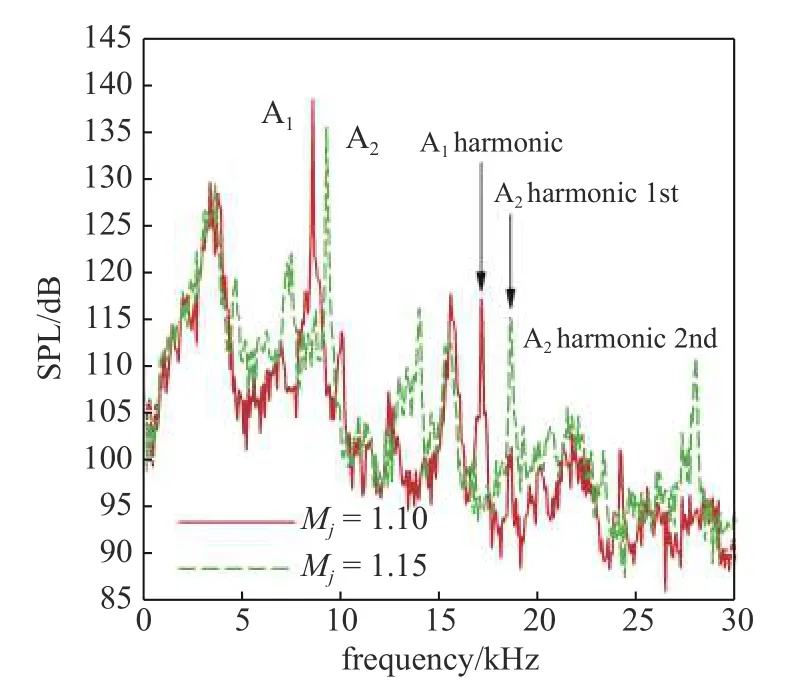
图3 射流近场噪声频谱信息:喷管唇口壁面监测点[0.0D,0.642D]Fig.3 Spectral information of jet near-field noise:monitor [0.0D,0.642D] located on the nozzle exit lip wall

表2 具体给出了上述离散频率模态的频率和声压级,为了进行对比,同时列出了Ponton等[13-14]的实验测量值和Loh等[41]的数值模拟结果.对于Mj=1.10 的射流,当前数值结果与Loh等[41]的数值结果都捕捉到了轴对称A1模态及其谐频,且频率和声压级吻合得很好.对于Mj=1.15 的射流,不论是模态类型,还是模态频率和声压级,当前数值结果都与实验结果[13-14]要更为吻合.

表2 啸声模态及其谐频的频率和声压级Table 2 The frequencies and amplitudes of screech modes and their harmonics

2.3 轴对称A1 模态啸声的声源位置

图4 是在完全膨胀射流马赫数Mj=1.10 的欠膨胀射流中与A1模态相关的瞬时流场结构和声场.从图中可以看到3 道向上游传播的啸声声波.采用Edgington-Mitchell等[21]的方法,在图4 中叠加一个与啸声声波重合的圆(蓝色虚线),通过圆心来定位声源位置.图4 显示,圆心位于流向位置x=2.29D处,该位置恰好是第4 个激波栅格结构的尾缘,也称激波反射点或激波尖梢;根据纹影和涡量还可以确定,在此位置处,剪切层内同时出现了一个旋涡鞍点.激波泄漏机制[17-18]也指出激波会在剪切层鞍点处向外泄漏,形成啸声声波.因此,可以确定第4 个激波栅格结构的尾缘是轴对称啸声A1模态的有效声源位置.

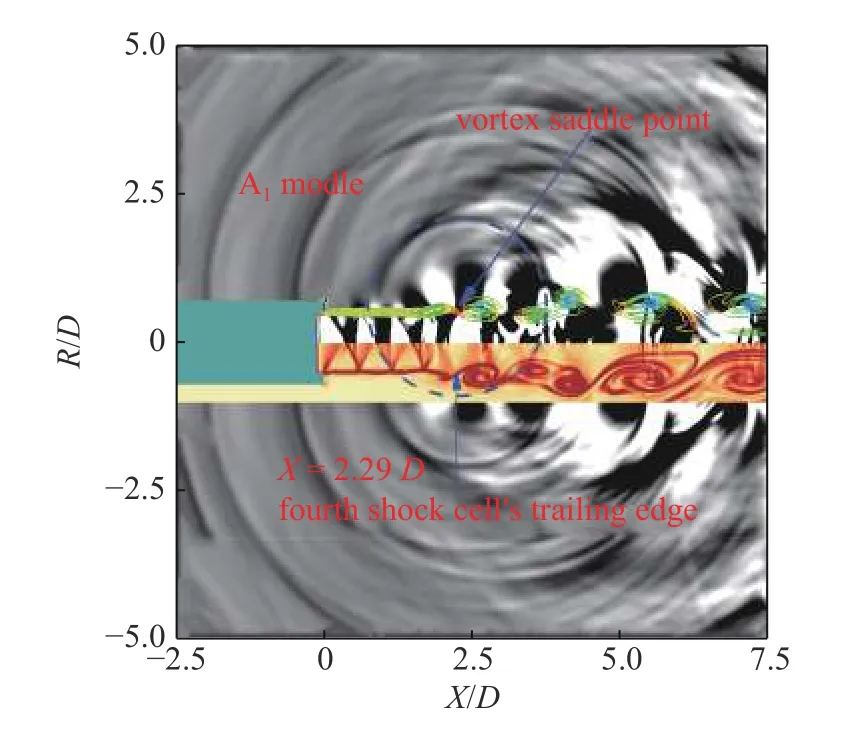
图4 Mj=1.10 的欠膨胀超声速射流中与啸声A1 模态相关的瞬时流动结构和声场Fig.4 The instantaneous flow structures and acoustic field associated with screech A1 mode in the underexpanded supersonic jet with Mj=1.10

2.4 轴对称A2 模态啸声的声源位置

通过快速傅里叶变换,对射流压力场进行傅里叶模态分解,即将时域空间的脉动压力场时间序列变换到频域空间,提取啸声频率成分,逐点计算声压级和相位,得到啸声频率上声压级和相位的空间分布.声压级最大的位置可认为是啸声模态的产生位置.本节的压力场傅里叶模态分解共选取了8192 个时刻的数据,起始时刻为t=200,无量纲时间间隔为δt=0.1.

图5是Mj=1.15 的欠膨胀超声速射流中啸声A2模态频率上的声压级空间分布和势核区的时间平均压力空间分布.在图5(a)声压级云图中可以看到沿射流剪切层外缘分布的啸声A2模态关联驻波结构.驻波结构是向下游传播的剪切层不稳定波和向上游传播的声波相互作用所产生[24].图5(b)中的时间平均压力分布展现的是射流势核内的激波栅格结构.结合图5(a)和图5(b)可知,声压级最大的位置是在流向位置x=2.14D处,即第3 个激波栅格结构尾缘.因此,可以确定啸声A2模态的声源位于第3 个激波栅格结构的尾缘.

图5 Mj=1.15 的欠膨胀超声速射流Fig.5 The underexpanded supersonic jet with Mj=1.15

图6是Mj=1.15 的欠膨胀超声速射流中啸声A2模态频率上的相位空间分布,从图中可以清晰地看到声波传播的波振面.为了进一步确定A2模态的声源位置,图7 提取了直线R/D=1.5 上的相位分布.相位斜率的符号表示声波的传播方向,而相位斜率符号变化的位置也可指示声源位置[26,28-29].图中显示,相位斜率的符号在流向位置x=2.14D附近发生了明显变化,在其上游,斜率为正值,声波向上游传播,而在其下游,斜率为负值,声波则向下游传播;该位置同时也是图5(a)中声压级最大的位置,表明啸声A2模态的声源位置的确是在第3 个激波栅格结构的尾缘.

图6 Mj=115 的欠膨胀超声速射流中啸声A2 模态频率上的相位空间分布Fig.6 The spatial distribution of phase at the frequency of screech A2 mode in underexpanded supersonic jet with Mj=1.15

图7 Mj=1.15 的欠膨胀超声速射流中啸声A2 模态频率上的相位沿直线R/D=1.5 的分布Fig.7 The distribution of phase at the frequency of screech A2 mode along the line of R/D=1.5 in underexpanded supersonic jet with Mj=1.15

2.5 基于本征模态分解的声源位置分析

本征正交分解(proper orthogonal decomposition,POD)是提取、分析湍流中拟序流动结构的重要工具[42].POD 方法的实质是在最小二乘意义下提供能够代表已知数据的一组正交基.POD 快照法[43]的目标是寻找脉动速度场数据快照u′的最小二乘表达式,即残差ures的模最小;相应的数学表达式[23,44]如下

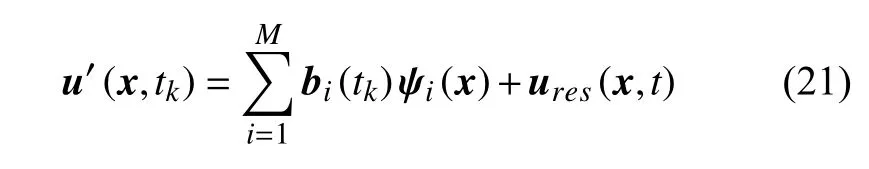
其中,bi是时间POD 模态,ψi是空间POD 模态.M是模态数,M≤N,N是数据快照序列的快照总数.

为了得到POD 模态,首先构造脉动速度场的快照矩阵V,随后计算脉动速度场的自相关(对称正定)矩阵R=VTV.

针对自相关矩阵进行特征分解Rai=λiai,求得自相关矩阵的特征值 λi和特征向量ai

空间POD 模态可以表示为脉动速度场快照与时间POD 模态乘积的线性组合

式中特征值 λi表征了每个空间POD 模态两倍的不可压脉动动能.因此,POD 方法能够提取最富能的流动结构.特别地,为了表征每个POD 模态的能量占比,需要对特征值 λi进行归一化处理,并按大小进行排序.需要注意的是,POD 模态通常是成对出现的.

本节的POD 分析选取了共2048 个时刻的速度场数据快照,无量纲时间间隔 δt=0.1 .

图8是Mj=1.10 的欠膨胀超声速射流速度场的时间POD 模态,包括波形、相图和特征值.POD 模态都是成对出现的,图8(a)和图8(b)是1 阶和2 阶POD 时间模态[a1(tk) 和a2(tk),k是快照时刻]及其相图.相图能够表征各阶POD 模态间的时间相关性,表示两个模态的平均幅值.1 阶和2 阶模态的波长是相匹配的;相图中的点大致呈圆形散布,表明前两阶模态是时间强相关的.时间相关性以及匹配的波长说明1 阶模态和2 阶模态是耦合的,两者共同表征了1 个振荡过程或拟序结构.图8(c)是各阶POD 模态的能量占比,1 阶和2 阶模态含能最高,两者之和接近45%,大于其它各阶模态.

图8(d)是1 阶和3 阶POD 模态的相图.图中的点呈双扭线形分布,表明1 阶、3 阶模态之间没有类似1 阶、2 阶模态的时间相关性.图8(e)和图8(f)是5 阶和6 阶POD 时间模态[a5(tk)和a6(tk) ] 及其相图,同样表示两者的平均幅值.与前两阶模态类似,5 阶和6 阶模态的波长相匹配,并且是时间强相关的,两者也共同表征了1 种拟序结构.

图8 脉动速度场的POD 时间模态和特征值,Mj=1.10Fig.8 Temporal POD modes and their eigenvalues of fluctuating velocity field,Mj=1.10

图9是Mj=1.10 的欠膨胀超声速射流速度场第1 对和第3 对POD 时间模态的傅里叶分析.一般来说,每个POD 模态包含多种频率组分.图9 显示,这两对POD 模态都有一个很强的主导频率,其中,第1 对的主导频率是4396 Hz,第3 对的主导频率是8595 Hz.第3 对POD 模态的主导频率与啸声A1模态的频率(8560 Hz)十分一致,即第3 对POD 模态表征的是与啸声A1模态相关的拟序流动结构.第1 对POD 模态的主导频率接近第3 对POD 模态的1/2,因此,其所表征的拟序流动结构是啸声A1模态关联拟序流动结构的亚谐频.

图9 脉动速度场的POD 时间模态的傅里叶分析,Mj=1.10Fig.9 The FFT analysis of the first and the third pairs of temporal POD modes of fluctuating velocity field,Mj=1.10

图10是Mj=1.10 的欠膨胀超声速射流速度场的第1 对和第3 对POD 空间模态,包括u分量和v分量.图中显示,空间POD 模态的u分量存在着非常明显的交界面,在交界面两侧符号相反,这一交界面是剪切层与射流主流(势核)的交界面;此外,每1 对空间POD 模态之间都存在着1/4 波长的相位差.第1 对POD 模态所表征的拟序结构在流向位置x＞3.8D的区域达到饱和态;第3 对POD 模态所表征的啸声相关拟序结构发展的更快,在流向位置1.5D＜x＜3.8D的区域就达到饱和态,随后开始衰减.前文2.3 节所述啸声A1模态的声源位置(x=2.29D)就位于该饱和态区域内.在第3 对POD 模态中,还可以清楚地看到从饱和态区域发出的,规律性地向上游和下游辐射的条纹,而向上游传播的条纹即为A1模态的啸声.根据主导频率和空间演化,第1 对POD 模态所表征的拟序结构是由啸声A1模态关联拟序结构在下游发生旋涡合并所产生.

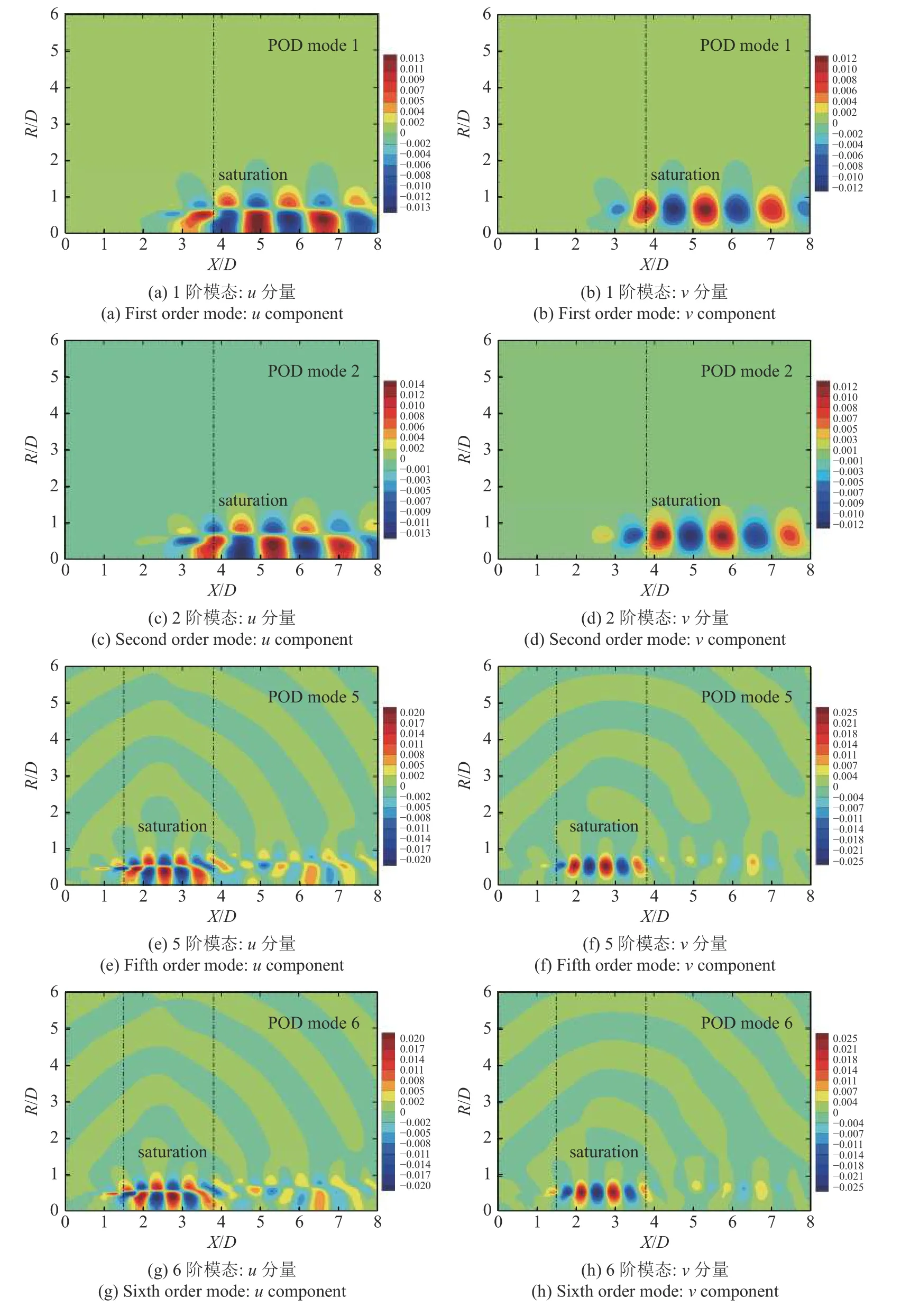
图10 脉动速度场的POD 空间模态,Mj=1.10Fig.10 The first and the third pairs of spatial POD modes of fluctuating velocity field,Mj=1.10

通过对不同流向位置处的脉动速度场切片进行POD 分析,可以研究拟序结构能量占比沿流向的发展变化.在每一流向站位,提取特定时间间隔内的

切片速度场时间序列组成局部数据快照矩阵,然后对局部数据快照矩阵进行POD 分析.

图11是Mj=1.10 的欠膨胀超声速射流速度场POD 模态特征值沿流向的变化曲线.图中显示,在流向位置x=3.1D处,第2 对POD 模态特征值之和的极大值点恰好对应第1 对POD 模态特征值之和在此处的极小值点;第1 对POD 模态所表征的拟序结构在此位置前经历了较为强烈的能量释放,而第2 对POD 模态所表征的拟序结构在此位置前一直在吸收能量,表明这两种拟序结构之间存在着能量传递.第3 对POD 模态特征值之和沿流向的变化表明,啸声A1模态关联拟序结构在其饱和态区域(1.5D＜x＜3.8D)内,先后经历了能量吸收再释放的过程,并且在能量释放子区间内,其能量占比,即第3 对POD 模态的特征值之和,在流向位置x=2.29D处产生了一个局部极小值点,这个局部极小值点就是前文2.3 节中确定的啸声A1模态的产生位置.

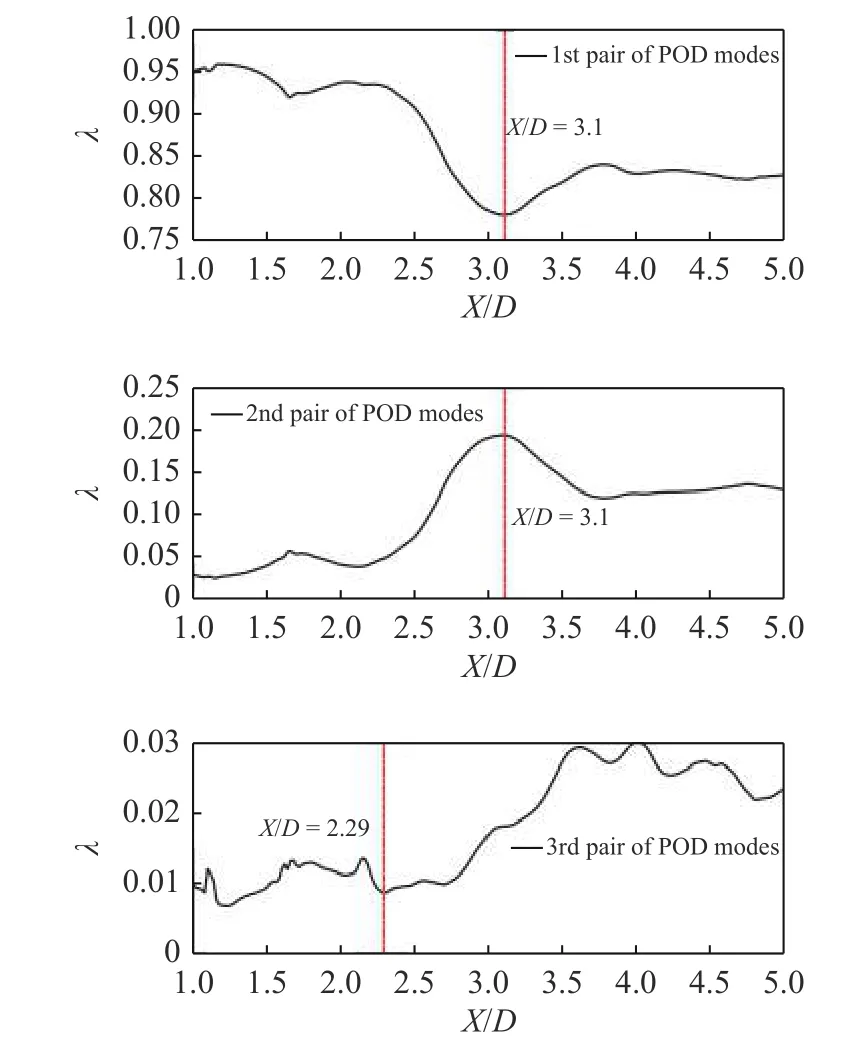
图11 脉动速度场轴向切片POD 分析中相关模态的特征值沿流向的变化,Mj=1.10Fig.11 The variations of eigenvalues along streamwise of the POD modes based on the POD analysis of velocity field’s slices in different axial position,Mj=1.10

2.6 基于动态模态分解的声源位置分析

动态模态分解[45](dynamic mode decomposition,DMD)方法则是基于动力系统Koopman 分析发展而来的分析工具,其通过时间正交的特征模态来重构数据快照序列.POD 模态强制空间正交性(结构去相关),每个独立的POD 模态都包含了多种频率成分,而DMD 模态是时间正交的(单一频率),一般空间不正交.如果数据序列足够长,DMD 方法能够识别主频,提取相关的流动特征.对源自于饱和非线性过程的实验或数值数据来说,相较于提取按能量排序的空间去相关结构,提取带有特定频率信息的时间去相关结构更为重要.

基于DMD 模态的数据快照重构表达式[46]为

式中,ϕk是DMD 模态,K是DMD 模态的数目,ωk=lnµk/Δt的虚部是DMD 模态的圆频率,而实部则表示指数增长或衰减,具体取决于符号;bk(0) 是每个DMD 模态的初始幅值.初始时刻的数据快照x1=Φb,所以DMD 模态的初始幅值可通过b=Φ+x1求得.

本节针对压力场的DMD 分析选取与2.5 节POD 分析中相同时刻的数据快照序列.具体求解过程如下.

其中,µj和yj分别是特征值和特征向量.

其中,U和W是酉矩阵,Σ 是奇异值对角矩阵.

最终可得DMD 模态

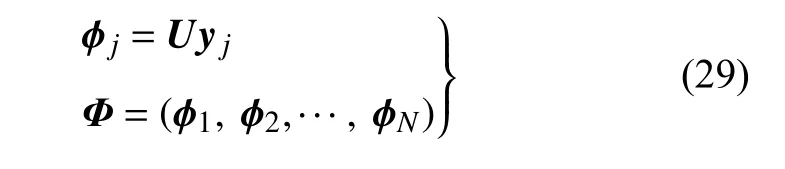
需要说明的是,本节后续分析中的DMD 模态都是包括了初始幅值的DMD 模态,即bjϕj.

图12是Mj=1.10 的欠膨胀超声速射流的压力场DMD 模态.各阶DMD 模态的频率分布见图12(a),其中,幅值最高的前4 阶DMD 模态的频率依次是4383 Hz,8570 Hz,4252 Hz 和4186 Hz.对比2.5 节中Mj=1.10 的欠膨胀射流速度场POD 分析结果可知,压力场的1 阶、3 阶和4 阶DMD 模态的频率都十分接近速度场第1 对POD 模态的主导频率(4396 Hz),并且三者具有相似的空间形态,这里只给出了3 阶DMD 模态,见图12(b),其所表征的拟序结构也是在流向位置x＞3.8D达到饱和态.2 阶DMD模态的频率接近第3 对速度场POD 模态的主导频率(8595 Hz),此频率也是啸声A1模态的频率(8560 Hz),因此,2 阶DMD 模态表征的是啸声A1模态的关联拟序结构,其饱和态区域为 1 .5D＜x＜3.8D,见图12(c),从中可以观察到从饱和态区域向外辐射的啸声A1模态声波条纹.根据频率,3 阶DMD 模态表征的拟序结构是2 阶DMD 模态所表征拟序结构的亚谐频;而且在空间演化上,两者的饱和态区域是接续的,因此,前者是由后者在下游发生旋涡合并后所产生.

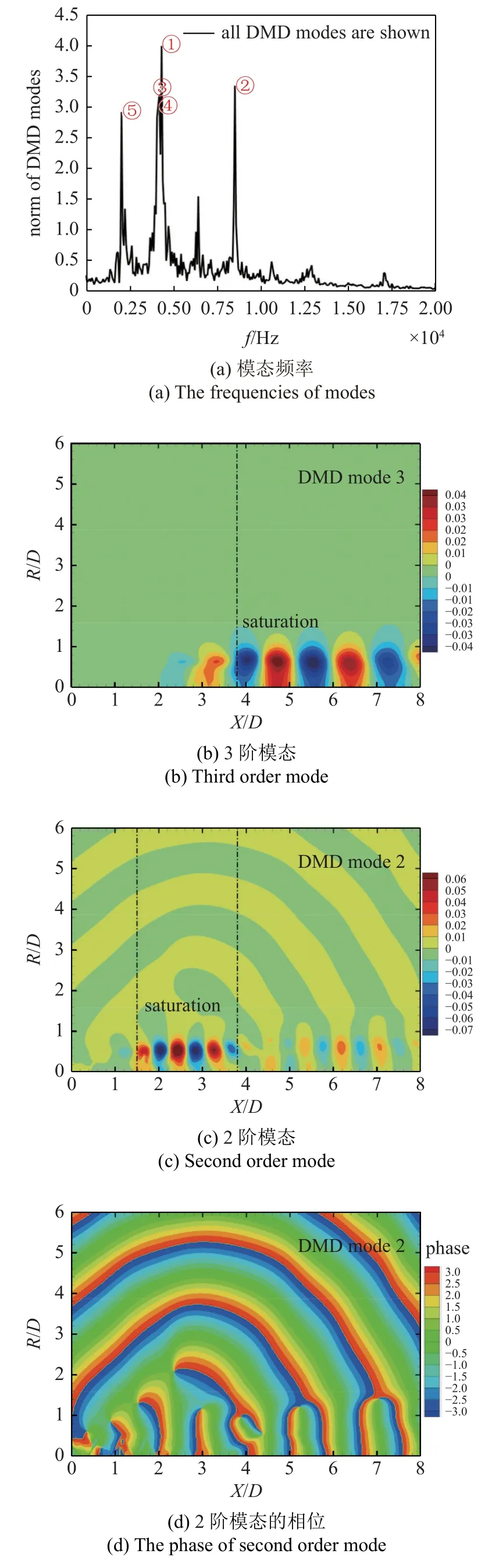
图12 Mj=1.10 的欠膨胀超声速射流的脉动压力场DMD 模态Fig.12 The DMD modes of fluctuating pressure field in the underexpanded supersonic jet with Mj=1.10

图12(d)是Mj=1.10 的欠膨胀超声速射流压力场2 阶DMD 模态的相位空间分布,清晰地表征了A1模态啸声声波传播的波振面.图13 提取了2 阶DMD 模态在直线R/D=2.1 上的相位分布.前文2.4 节中已经说明相位斜率符号改变的位置可以指示啸声的声源位置.2 阶DMD 模态相位斜率的符号是在流向位置x=2.29D处发生改变,该位置也是前文2.3 节和2.5 节中所确定的啸声A1模态的产生位置,这再次证实啸声A1模态的有效声源位置是在第四个激波栅格结构的尾缘.

图13 2 阶DMD 模态的相位在直线(R/D=2.1)上的分布,Mj=1.10Fig.13 The distribution of phase along the line R/D=2.1 for the second DMD mode,Mj=1.10

图14是Mj=1.15 的欠膨胀超声速射流的压力场DMD 模态.图14(a)是各DMD 模态的频率分布,其中,幅值最高的前4 阶DMD 模态的频率依次是4579 Hz,4644 Hz,4710 Hz 和9289 Hz.前3 阶DMD 模态的频率近似相等,而且也具有相似的空间形态,因此,这里只给出了2 阶模态,见图14(b).4 阶DMD 模态接近啸声A2模态的频率(9250 Hz),因此,它表征的是啸声A2模态关联拟序结构,图14(c)显示其饱和态区域为 1 .65 ＜x＜3.25,并且可以观察到自此区域向外辐射的啸声A2模态声波条纹.2 阶DMD 模态是4 阶DMD 模态的亚谐频,其所表征的拟序结构在流向位置x＞3.25 处达到饱和态.同样地,根据频率和空间演化可知,前者也是由后者在下游发生旋涡合并所产生.

图14 Mj=1.15 的欠膨胀超声速射流的脉动压力场DMD 模态Fig.14 The DMD modes of fluctuating pressure field in the underexpanded supersonic jet with Mj=1.15

图14(d)是Mj=1.15 的欠膨胀超声速射流压力场4 阶DMD 模态相位的空间分布.与图12(d)类似,相位空间分布清晰地表征了A2模态啸声声波传播的波振面.图15 提取了4 阶DMD 模态在直线R/D=1.5 上的相位分布.沿流向,2 阶DMD 模态有多个相位斜率符号发生改变的位置,但只有一个位于饱和态区域之内,即x=2.14D.图14(c)也显示啸声声波是在饱和态区域内向外辐射,因此,饱和态区域外的相位斜率符号转变位置与啸声的产生没有直接关联.此外,x=2.14D这一位置也与2.4 节中傅里叶模态分解得到的结果一致,进一步证实啸声A2模态的产生位置是在第3 个激波栅格结构的尾缘.

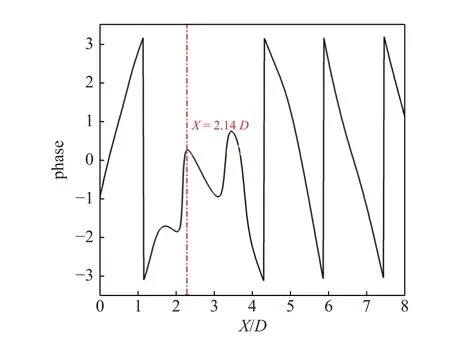
图15 4 阶DMD 模态的相位在直线(R/D=1.5)上的分布,Mj=1.15Fig.15 The distribution of phase along the line (R/D=1.5) for the fourth DMD mode,Mj=1.15

3 结论

为了研究轴对称模态啸声的产生位置,本文采用高阶精度有限差分方法直接求解轴对称可压缩Navier-Stokes 方程,数值模拟了完全膨胀射流马赫数分别为1.10 和1.15 的圆形声速喷管欠膨胀超声速冷射流,得到了轴对称啸声A1模态和A2模态.通过激波栅格结构位置和啸声模态频谱与文献实验结果的对比,验证了数值模拟的准确性.

基于傅里叶模态分解、本征模态分解和动态模态分解,分析了射流时序压力场和速度场,研究了啸声关联拟序流动结构的空间演化,精确定位了轴对称模态啸声的有效声源位置.

研究表明:啸声关联拟序流动结构存在饱和态区域,并且啸声声波是在其饱和态区域内产生并向外辐射.在本文所涉及的射流马赫数范围内,A1和A2两种轴对称模态啸声的有效声源位置分别是在第4 和第3 个激波栅格结构的尾缘.因此,本文的数值模拟结果支持A1和A2两种啸声模态是单声源的观点.

需要注意的是,本文只研究了低马赫数超声速射流中的轴对称模态啸声,对于出现在高马赫数射流中的摆动模态啸声和螺旋模态啸声没有涉及,它们具体的声源位置以及是否为单声源,仍有待进一步研究.