交通载荷作用下跨海桥梁-电缆组合结构随机振动分析1)

张振鹏 赵健康 李文杰 赵鹏 黄凯文

(中国电力科学研究院有限公司,武汉 430074)

(电网环境保护国家重点实验室,武汉 430074)

引言

随着内陆与岛屿、岛屿与岛屿之间的跨海大桥不断建设,越来越多的电缆采用沿跨海大桥敷设方式进行[1-4].对于海岛电力输送而言,采用沿跨海大桥敷设电缆比沿海底敷设电缆具有更高的经济效益,且更加便于电缆的维护和检修[5-7].当电缆敷设于桥梁上时,桥上经过的汽车和列车交通载荷会诱发桥梁的振动,从而引起电缆的振动,长期处于振动环境会导致电缆内部产生额外的应力且会导致构件的疲劳问题[8-10].此外,电缆的机械振动会使得电缆同时承受温度应力和振动引发的弯曲应力,使其内部的应力分布更加复杂,对电缆的介电性能产生不利影响[11].机械力和外部振动产生的应力也会导致电缆绝缘材料的老化,从而使电缆绝缘性能降低甚至失效[12-14].张振鹏等[15]研究了交联聚乙烯电缆在温度和外部振动联合作用下引起的电缆绝缘老化失效问题,研究结果表明机械振动加速了电缆绝缘层的老化.开展沿桥敷设电缆在交通载荷作用下引起的振动问题研究,对保证电缆的正常输电功能和提高电缆耐久性具有必要性[16].

对于沿跨海桥敷设的电缆而言,由桥上行驶经过的汽车和列车交通载荷引起的振动对电缆的影响不容忽略,在实际工程中往往也会采取相应的减振措施[2,17].尽管沿桥敷设电缆的振动问题已经逐渐被认识到,但对桥上电缆振动响应的特性和影响规律尚未研究透彻.实际上,引起桥梁振动的汽车和列车交通载荷包含有不同的频率成份,在具有不同频率成份交通载荷作用下的电缆动力响应也会有区别.刘骥等[18]研究了外部载荷频率对不同支撑条件下交联聚乙烯电缆的内部应力和位移的影响规律,研究结果表明在共振频率与非共振频率外部载荷作用下,电缆内部应力、位移的幅值相差很大.随着电缆服役年限的增长,外部振动可能导致绝缘层老化,护套开裂等现象,导致电缆无法完成电力输送任务[19-20].同时,现代交通日益增长的车流量,进一步加快了电缆的老化进程.

本文建立了桥梁-电缆结构整体组合分析模型,对沿跨海大桥敷设电缆在汽车和列车交通载荷作用下产生的随机振动响应展开研究.将交通载荷视为移动的随机集中载荷序列,考虑引起车辆和桥梁振动的路面和轨道不平顺性的随机性,发展虚拟激励法(pseudo-excitation method,PEM),通过构造特定的虚拟移动载荷,求解虚拟响应,能快速地得到电缆响应的标准差以及电缆响应的演变功率谱.数值算例针对不同汽车和列车运行速度,研究了不同行驶速度对电缆动力响应的影响规律.本文工作为后续交通载荷引起沿桥梁跨海铺设电缆振动及疲劳破坏和疲劳寿命评估问题的深入研究具有一定的参考价值.

1 计算模型及参数

1.1 跨海铺设电缆有限元模型

本文分析所采用的电缆为220 k V 高压交联聚乙烯电缆,各层材料的主要物理特性参数[18]及厚度列于表1 中,图1 中给出了电缆的结构模型.根据电缆的结构特征,并考虑到桥梁的长度较长,若采用实体单元来模拟电缆,节点自由度规模庞大,显著消耗计算资源.对此,根据跨海桥梁电缆的细长结构特征,在ANSYS 中用梁单元进行模拟.当电缆沿着跨海桥梁敷设时,通常会采用如图2 所示的蛇形敷设.其中,Ws为蛇形幅宽取0.24 m;Ls为蛇形节距取6 m.根据蛇形幅宽和节距,将电缆沿z轴方向的坐标表示为正弦函数.为了建模的便利性,将电缆各节点x轴坐标间距取为0.5 m,并根据z轴坐标沿电缆轴向变化的规律,得到电缆各个节点的坐标,从而建立电缆的有限元模型.根据电缆各层材料参数和截面尺寸,分别定义相应的材料特性和截面参数,实现对铺设电缆不同结构层的模拟.

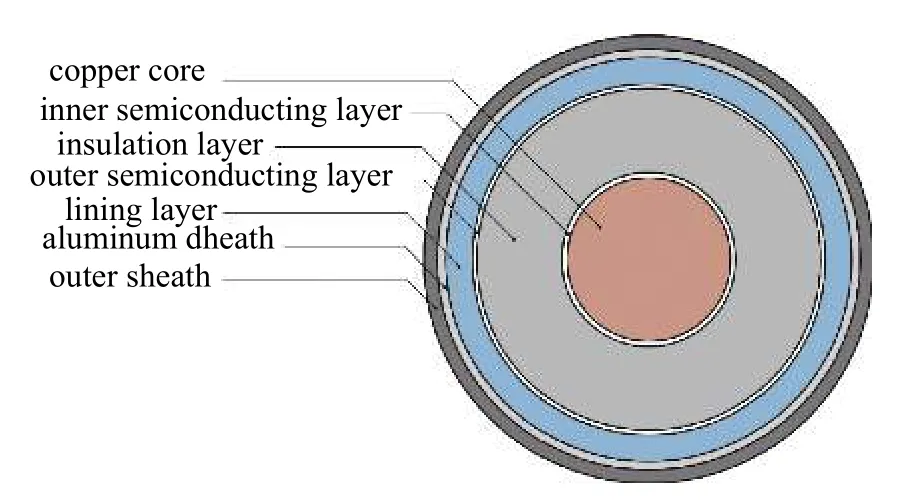
图1 电缆结构Fig.1 Structure of cable

图2 电缆蛇形敷设形状Fig.2 Snake-shaped laying shape of cable

表1 电缆各层材料参数[18]Table 1 Material parameters of each layer of cable[18]

1.2 桥梁-电缆组合结构有限元模型

这里跨海桥梁分析模型采用典型的多跨连续梁桥,桥面和桥墩的材料及结构参数列于表2 中.桥梁的有限元模型采用BEAM188 单元建立,单元长度设置为1 m.根据桥墩的结构形式,假定桥墩在与桩基础的交界面处为固定端约束.

表2 桥梁的结构及材料参数Table 2 Material parameters of bridge

电缆沿跨海桥梁敷设时,每间隔一定距离均会采用电缆夹具对其进行固定.由于夹具的刚度非常大,因此假定电缆在夹具位置处无法发生转动,且假定电缆与桥梁是刚性连接的.将桥梁与电缆在连接节点处的自由度进行耦合,从而建立如图3 所示跨海桥梁-电缆组合结构的分析模型.

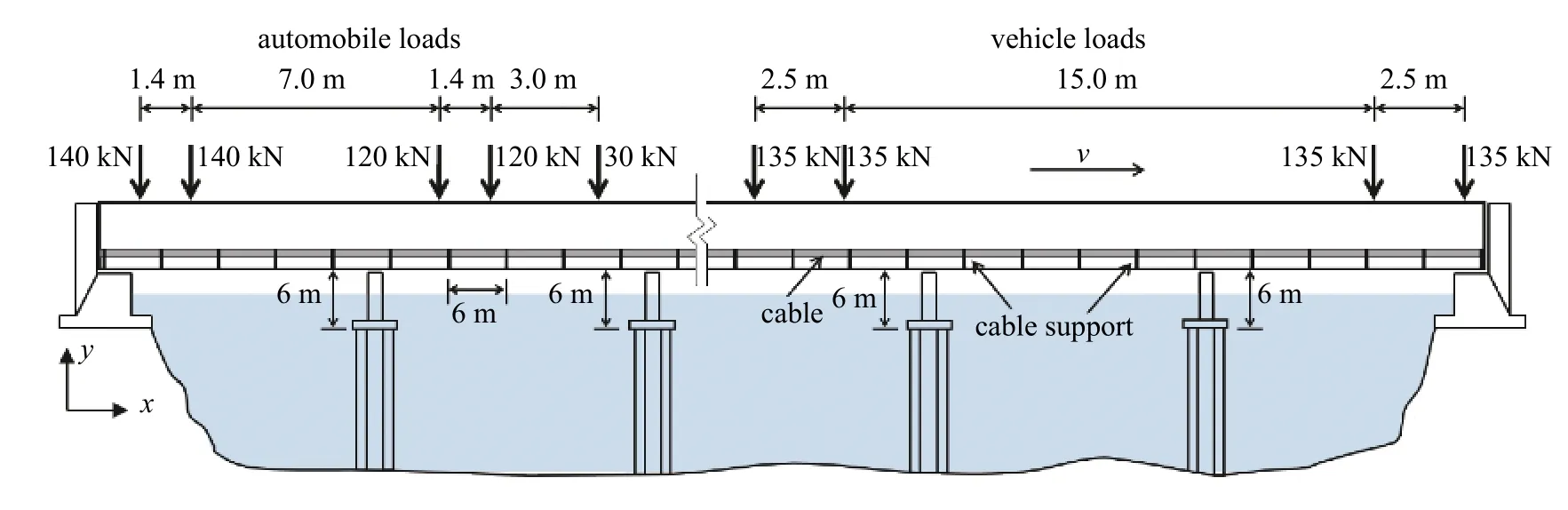
图3 跨海桥梁-电缆组合结构分析模型Fig.3 Analysis model of the coastal bridge-cable composite strucuture

1.3 交通载荷的移动随机载荷序列模型

当桥上有汽车或者列车经过时,桥梁主要在汽车车轮或列车轮对处受到集中力序列作用,在本文中采用移动随机集中力序列来模拟汽车载荷或列车载荷对桥梁的作用.汽车采用5 轴货车来模拟,列车采用8 节车厢编组的高速列车来模拟.汽车及列车的轴距及轴重(均值)如图3 所示.列车前一车厢最后一组轮对与后一车厢第一组轮对的距离取 1 .1 m,不考虑车厢之间的水平方向连接作用力.当汽车经过桥梁时,分析时间自前轮上桥时起至后轮下桥时止.当列车经过桥梁时,分析时间自第1 节车厢的第1 组轮对上桥至列车最后1 节车厢最后1 对轮对下桥时止.为使问题分析和讨论简化,暂不考虑汽车和列车同时经过桥梁时的情形.

2 桥梁-电缆随机振动响应求解的虚拟激励法

当汽车或列车从桥上经过时,由于桥面的不平顺性和轨道的不平顺性,使得汽车和列车产生垂向的振动响应,导致图3 中的移动集中力不再是确定的值.不平顺性具有固有的随机性本质,相应的移动集中力也具有随机性,需要结合随机振动的功率谱分析理论来分析电缆的动力响应.

2.1 桥梁-敷设电缆结构运动方程

在进行桥梁-敷设电缆组合结构的有限元离散后,可以得到结构在移动随机载荷序列作用下的运动方程[21]

式中,n为桥梁-电缆组合结构中桥梁的自由度数目.

车辆在桥上经过时是连续移动的,用于桥梁-电缆结构动力响应分析的移动集中载荷也应当是连续移动的.采用有限元方法进行分析,载荷只能作用于有限元模型的节点上,需要将单元内连续移动的集中力等效作用于节点.移动集中力作用于单元内部时,可用插值形函数将移动集中载荷等效作用于单元两端的节点上[22].移动集中力尚未上桥时,认为其作用在桥梁有限元模型左侧第1 个单元的左侧节点上.当移动集中力经过桥梁到达桥梁最右端时,认为其作用在桥梁有限元模型右侧最后1 个单元的右侧节点上.

移动力的x轴坐标可以根据载荷移动速度v以及时间t确定.在确定每一时刻每个移动集中力的x轴坐标后,便能够进行桥梁-电缆结构在车辆载荷作用下的随机振动分析.

2.2 移动随机载荷作用桥梁-电缆结构随机振动分析

在求解方程(1)时,由于结构自由度数目较多,通常采用振型叠加法.根据该方法的原理,当取结构前q阶振型参与计算时,假定结构具有正交阻尼,并利用振型的正交性,可以得到模态空间内的q个解耦的单自由度运动方程

式中,j=1,2,···,q,φj为结构的第j阶振型向量;xj(t),(t)和(t) 分别为结构第j阶模态位移、速度和加速度;mj,cj和kj分别为结构第j阶模态质量、阻尼和刚度.

式(3)的解可以采用Duhamel 积分表示为

式中,hj(t-τ) 为脉冲响应函数.原方程(1)的解可表示为

结构响应x(t) 的方差矩阵Rxx(t) 为

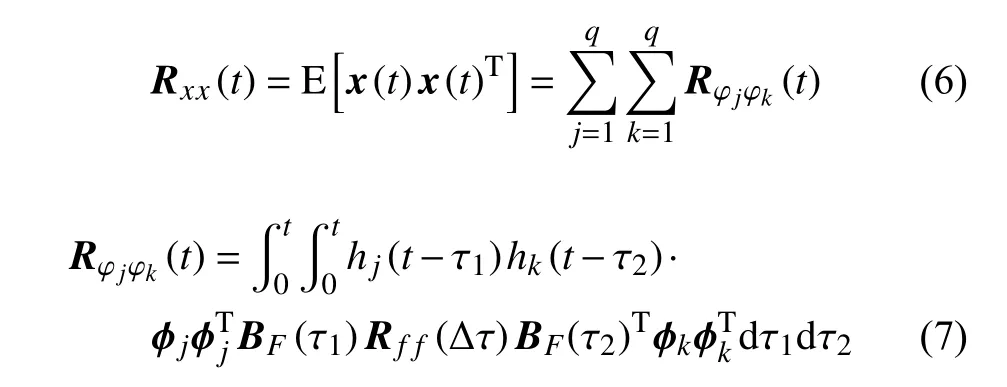
式中,E [•] 为数学期望运算;Δ τ=τ1-τ2,Rφjφk(Δτ)为模态响应方差矩阵;Rff(Δτ) 为外载荷协方差矩阵.根据Wiener-Khintchine 关系[23],载荷以及响应的自相关函数和功率谱矩阵存在如下关系

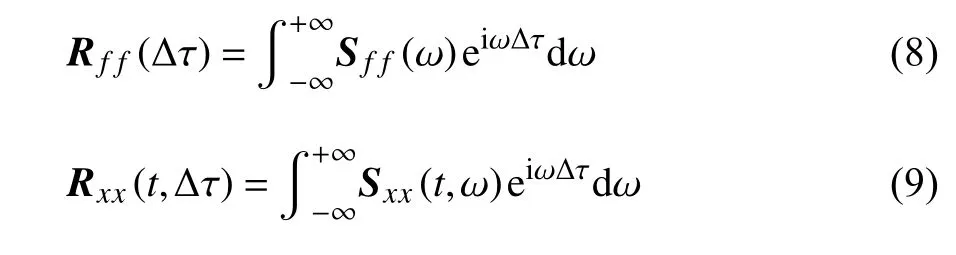
将式(8)代入式(7)中并交换积分次序,得到

将式(10)代入式(6)中,并根据式(9)中的Wiener-Khintchine 关系,得到结构响应的功率谱矩阵

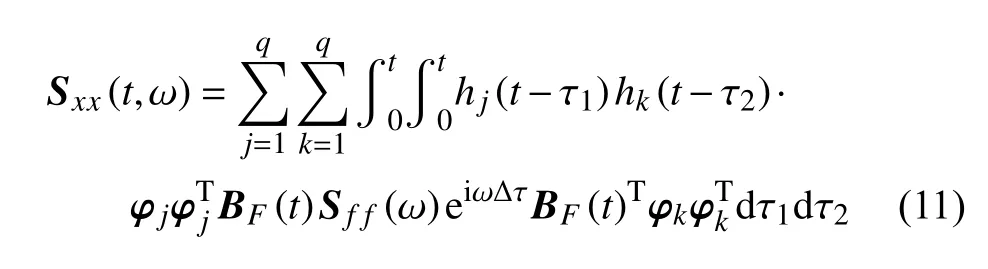
响应的方差矩阵Rxx(t) 和功率谱矩阵Sxx(t,ω)是随机振动分析中非常重要物理量,由式(6)和式(11)可知其计算过程涉及双重求和和双重积分,计算量非常大.在实际应用中,计算响应功率谱矩阵时通常忽略了振型的交叉项以减少计算量,得到了计算功率谱的SRSS (square root of the sum of squares,平方和开平方)方法.SRSS 方法对于参振频率全部为稀疏分布,且各阶阻尼比都很小的均质材料结构才是可用的[24].当结构自振频率比较密集时,采用SRSS 公式计算功率谱可能会带来较大的误差.为此,本文采用PEM 来计算移动随机载荷作用下电缆的响应功率谱.

当汽车或列车从桥上经过时,引起桥梁垂向振动的激励源主要是路面和轨道的不平顺性[25-27].当前后车轮行驶至桥梁相同位置时,所受到的不平顺激励是完全相同的,但存在与行驶速度相关的时间差.因此,可将桥上移动随机载荷假定为完全相干的随机载荷.这时,移动随机载荷的功率谱矩阵Sff(ω)可表示为

式中,Sf(ω) 为激励的功率谱;ai(i=1,2,···,Nf) 表示每个随机载荷的强度,对于完全相干的激励可取ai=1;ti(i=1,2,···,Nf) 表示每个随机载荷的时刻.

根据PEM[28],功率谱矩阵Sff(ω) 可分解为向量的乘积

式中,上标“*”表示向量的复共轭.

将式(13)代入式(11)中,得到响应功率谱矩阵

对比式(16)和式(4)可知,在计算响应的功率谱矩阵Sxx(t,ω) 时,只需要计算虚拟移动载荷引起的虚拟响应 ˜x(ω,t) .在计算得到电缆响应的功率谱后,根据式(9)可以得到电缆的响应方差,从而可以对电缆响应进行估计.

3 数值算例

在本文算例中,桥梁采用5 跨连续梁桥,各跨跨度取30 m.由2.2 节可知,在计算电缆在车辆载荷作用下的随机响应时,根据PEM 只需要求解结构在特定移动简谐载荷下的动力响应.本文利用MATLAB作为实现虚拟激励法主控制程序,通过调用ANSYS进行瞬态响应分析,进行电缆非平稳随机振动响应的求解.在模态叠加法中,取结构前200 阶振型参与计算,各阶模态阻尼比均取为0.02.所有移动集中力均假定为高斯平稳随机过程[29],均值如图3 中的载荷序列所示,载荷的功率谱Sf(ω)=6.366×107N2/s .根据路面和轨道的不平顺频谱特性[30-31],汽车载荷的分析频率取 [ 0,40π],频率步长取 0 .4π .列车载荷的分析频率取 [ 0,200π],频率步长取1 .0π .在求解汽车载荷引起的动力响应时,积分时间步长取 0 .005 s .求解列车载荷引起的动力响应时,相应的积分时间步长取 0 .002 s .根据结构响应特征,取跨海桥梁第3 跨跨中位置处的电缆跨中位移和缆芯及铝护套应力响应作为主要的研究对象.

3.1 电缆响应时变标准差

为了验证PEM 计算结果的精确性,本文将PEM 的计算结果与MC 方法结果进行对比.根据汽车或列车的运行速度确定各轮轴力时间差,由移动载荷的功率谱Sf(ω) 利用三角级数叠加法生成1000 个随机移动集中力序列样本.根据每个载荷样本均进行一次动力响应分析,分别得到电缆跨中位移和缆芯应力响应,最后根据样本值求得响应的时变标准差.图4 中给出了汽车载荷v=33.33 m/s 工况时,两种方法的计算结果对比.从图中曲线可知,PEM 计算得到的电缆时变响应标准差与MCS 模拟结果吻合较好,表明PEM 具有足够的精确性.值得注意的是,在MCS 中需要进行1000 次时域响应分析.而采用PEM 计算响应时变标准差时,只需在每个频率点处构造虚拟正弦和余弦移动载荷并进行时域响应分析.在本文中,PEM 仅需进行200 次时域响应分析便能够得到与MCS 非常吻合的结果.

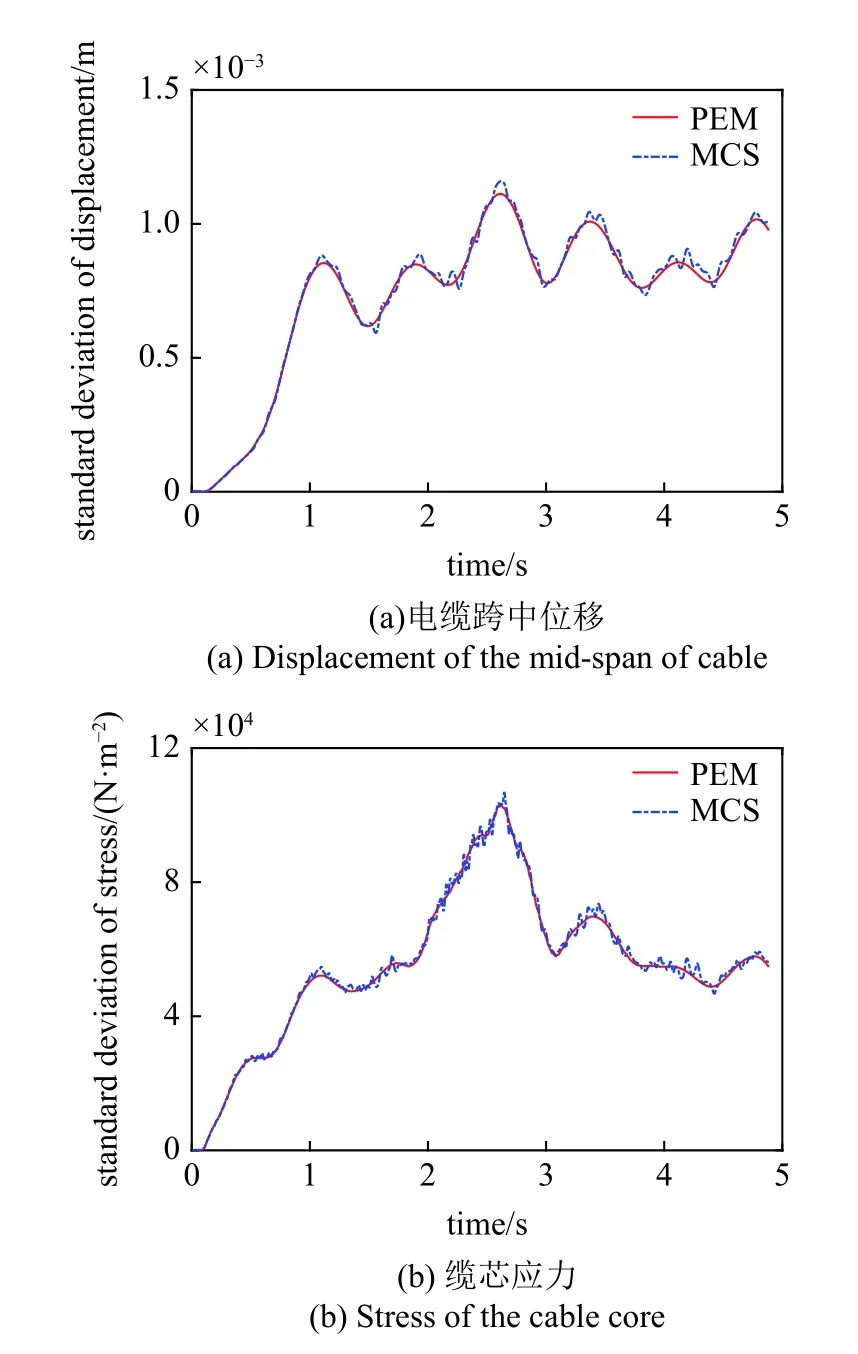
图4 MC 方法与PEM 计算结果对比Fig.4 Comparison of results of MC method and PEM

图5～图7 中给出了采用PEM 计算得到的不同汽车和列车行驶速度时引起的电缆响应时变标准差.对比图中不同速度工况时的电缆响应曲线可知,随着汽车和列车行驶速度的增大,电缆的位移和应力响应标准差总体呈现增大的趋势.对比电缆不同部位的响应时变标准差可知,无论是汽车载荷还是列车载荷,电缆铝护套的应力响应标准差会比缆芯应力标准差更大.在列车载荷作用时,电缆响应标准差出现的峰值波动更多,这与列车具有更多的轮对导致的载荷完全相干作用有关.

图5 电缆跨中位置位移响应时变标准差Fig.5 SD of displacement of the mid-span of cable

图6 电缆跨中位置缆芯应力响应时变标准差Fig.6 SD of stress of cable core of the mid-span of cable

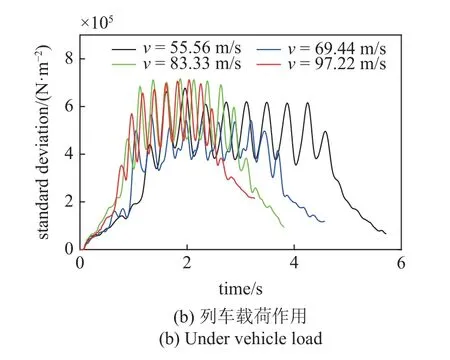
图6 电缆跨中位置缆芯应力响应时变标准差 (续)Fig.6 SD of stress of cable core of the mid-span of cable (continued)

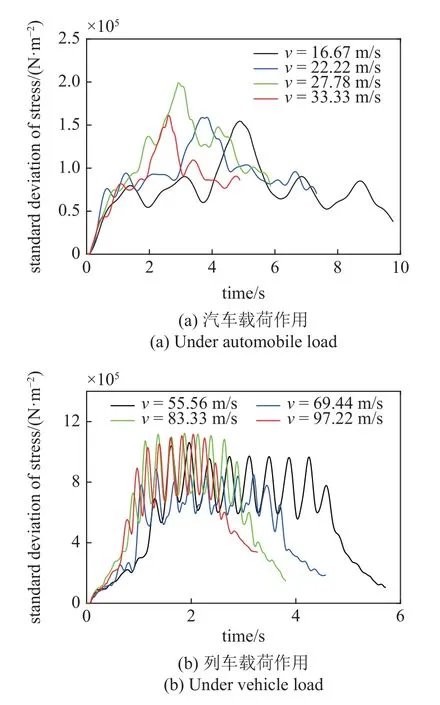
图7 电缆跨中位置铝护套应力响应时变标准差Fig.7 SD of stress of aluminum sheath of the mid-span of cable

3.2 电缆响应演变功率谱

图8 中给出了由PEM 计算得到的电缆跨中位移响应演变功率谱.由图可知,电缆位移响应主要集中在较低的频率范围内.尽管汽车载荷和列车载荷的功率谱取值相同,但由于两种载荷形式和特征不同,列车载荷作用下电缆位移功率谱的取值比汽车载荷作用的下功率谱更大.

图9 和图10 中分别给出了PEM 计算得到的缆芯和铝护套的应力演变功率谱.尽管移动随机载荷被假定为高斯平稳过程,但由于载荷在桥上移动具有与时间的相关性,由此引起的电缆响应也具有时间相关性,功率谱具有演变特征.与位移演变功率谱不同的是,应力响应演变功率谱的分布频带范围更宽一些.对比图9 和图10 中缆芯应力功率谱和铝护套应力功率谱可知,无论是受汽车(或列车)载荷作用,缆芯和铝护套应力功率谱随时间和频率的变化趋势基本一致,但在这两种移动载荷作用下,电缆铝护套的应力功率谱值均大于缆芯应力功率谱的值.根据结构振动疲劳寿命分析的频域方法[32],会使得铝护套首先发生疲劳破坏.本文方法可以给出缆芯和铝护套的应力功率谱,从而为沿桥敷设电缆的进一步疲劳寿命评估和预测提供了一定的基础.

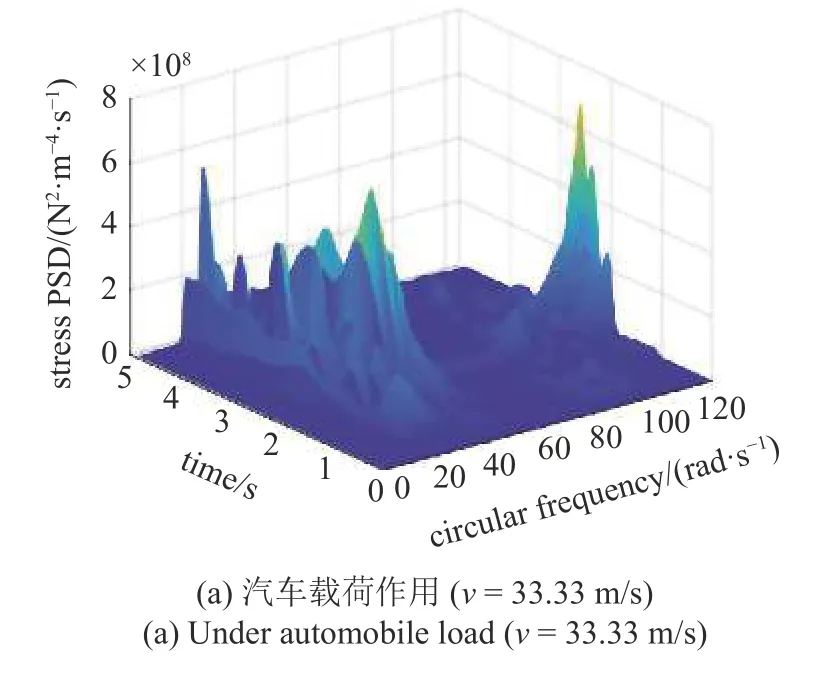
图9 电缆跨中位置缆芯应力响应演变功率谱Fig.9 PSD of stress of cable core of the mid-span of cable

图9 电缆跨中位置缆芯应力响应演变功率谱 (续)Fig.9 PSD of stress of cable core of the mid-span of cable (continued)

图10 电缆跨中位置铝护套应力演变功率谱Fig.10 PSD of stress of aluminum sheath of the mid-span of cable

4 结论

本文针对沿桥敷设电缆在随机汽车和列车载荷作用下的动力响应进行分析,建立了桥梁-电缆有限元分析模型,采用虚拟激励法(PEM)计算了电缆的随机振动响应,研究了汽车和列车运行速度对电缆动力响应的影响.分析结果表明,PEM 能够得到与Monte Carlo 方法相吻合的电缆响应演变标准差,且能够方便地得到电缆响应的演变功率谱.当载荷的移动速度增大时,电缆位移和应力演变响应标准差会相应增大.与缆芯相比,铝护套的位移响应演变标准差和应力响应演变功率谱值更大,这可能使得电缆的疲劳破坏首先出现在铝护层.