考虑无功支撑的分布式光伏接入配电网电压适应性研究

李 征，王文宾，韩胜峰，林丽娟

考虑无功支撑的分布式光伏接入配电网电压适应性研究

李 征1，王文宾1，韩胜峰1，林丽娟2

(1.国网河北省电力有限公司邢台供电分公司，河北 邢台 054001；2.电力电子节能与传动控制河北省重点实验室(燕山大学)，河北 秦皇岛 066004)

在构建以新能源为主体的新型电力系统背景下，分布式光伏呈现高比例渗透趋势。光伏出力的波动性易引起配电网电压越限和三相不平衡问题，同时光伏逆变器的剩余容量又具有无功主动支撑作用，有利于改善电压质量。而且配电网阻感比大、电压与有功耦合明显，导致配电网电压受光伏有功无功的综合影响而更加复杂。从电压适应性角度研究配电网接纳三相和单相分布式光伏的承载能力。首先，按统计学原理分别建立最大值、期望值和众数值等反映电压质量的统计特征指标，并从光伏渗透率和接入分散程度两方面描述分布式光伏的接入特征。其次，基于历史天气数据构建典型日场景，考虑光伏主动参与无功支撑作用，运用随机模拟分析得出各节点电压质量统计指标。最后，采用AHP-CRITIC组合赋权法分别对电压偏差和不平衡指标进行一定的加权组合，综合反映电压适应性。应用OpenDSS软件进行算例分析，结果验证了所提方法的有效性。

配电网；分布式光伏；主动支撑；场景构建；电压适应性

0 引言

在“双碳”目标驱动下，我国电力系统正在由传统型向新能源型过渡，这将促使分布式光伏极高比例接入配电网[1-2]。2021年6月，国家能源局正式下发《关于报送整县(市、区)屋顶分布式光伏试点方案的通知》，标志着配电网承载极高比例分布式光伏的现实压力已摆在面前。电力系统承载高比例新能源需解决功率平衡和安全并网两个问题。并网问题关注新能源能否安全接入配电网而不引起电压和潮流越限，其中电压问题是突出问题之一[3-4]。

分布式光伏(Distributed Photovoltaic, DPV)可主动参与电压支撑[5]，实现灵活快速的无功调节，消除DPV随机波动引起的电压干扰[6-8]。文献[9]针对分布式电源(Distributed Generator, DG)接入配电网引起的电压偏差问题，考虑DG有功无功调压能力，提出基于模型预测控制的电压优化控制方案。针对电压随机波动问题，文献[10]分析了高渗透光伏并网引起的电压越限和波动，提出一种双递阶抑制策略，充分利用DPV虚拟同步机的无功调节能力，实现系统快速响应，以支持光伏广泛接入。文献[11]提出含多异质DG参与电压调控的配电网多时空尺度无功优化方法，实现时间域和空间域的精准电压控制。文献[12-13]提出高渗透率DG接入配电网的多目标无功分区方法，以减少无功控制的网损。文献[14-16]分别从全局系统电压控制以及无功分区控制角度对DG接入配电网的电压进行调节。文献[17]提出DPV的两级电压控制策略，利用其无功补偿能力微调系统电压分布，并满足控制响应时间。单相光伏接入配电网会带来电压不平衡问题，文献[18]针对光伏并网的影响进行研究，指出分布式光伏的大量单相接入会大大加重配电网的三相电压不平衡问题。为准确分析分布式光伏接入导致的配电网不平衡，文献[19]分别从光伏容量比、系统网络损耗和电压稳定裕度等角度建立了考虑三相不平衡的分布式光伏多目标优化配置模型。对配电网电压质量的评价，文献[20-21]从电压偏差、电压波动和三相不平衡等指标分析配电网健康状况。文献[22]基于DPV出力的Beta分布概率模型，建立了配电网电压质量的概率评估体系。文献[23]提出了一种电压三相不平衡的判别方法，并引入风险偏好型效用函数进行影响程度评估。文献[24]从评估指标、评估权重及评估模型三方面特性概述了电能质量综合评估的研究现状，指出DG并网条件下综合评估是未来的重要研究方向。

构建以新能源为主体的新型电力系统是实现能源转型的必然趋势，配电网对于分布式光伏的可承载能力需要明确。DPV高比例接入引起的电压偏差和不平衡问题是限制其接入规模的重要因素。现有文献主要研究DPV参与配电网调压控制策略以及特定接入情形下配电网的电压质量问题，没有从可承载能力角度对DPV接入配电网的电压适应性提出评判指标和分析方法。本文针对分布式光伏单相和三相高比例接入引起的电压问题，提出一种评估配电网承载DPV能力的电压适应性分析方法。分别建立电压偏差及不平衡的5%最大值、95%期望值和5%众数的风险统计指标，定义光伏渗透率和分布均匀度指标来表征分布式光伏的接入形态。通过历史天气数据构建典型日场景，运用随机模拟分析得到电压质量指标。采用AHP-CRITIC组合赋权法分别对电压偏差和不平衡指标进行组合，综合反映电压适应性。本文研究可为分布式光伏高比例接入的配电网规划问题提供指导。

1 电压质量风险指标构建

1.1 指标越限区间的概率统计

由于光伏具有很大的随机性和不确定性，本文采用统计原理对光伏出力模型进行随机模拟，统计配电网电压质量指标，进而分析高比例光伏接入的电压适应性。考虑到相关标准对电压质量统计指标允许出现一定概率的越限[25-26]，本文遵循这个原则，结合光伏高比例接入电网的特征提出电压质量指标。光伏引起的电压质量问题主要有电压偏差、三相不平衡及谐波畸变和电压波动等，本文方法主要对电压偏差和三相不平衡进行描述，对于其他指标同样适用。考虑到分布式光伏以单相方式接入配电网的比例很大，存在严重的不平衡问题，本文分别以配电网各相单独进行电压偏差考核，同时以负序和零序电压作为不平衡指标进行考核。为刻画电压质量统计特性，将电压越限的分布范围以1%为步长划分越限区间，分别统计节点越限电压落在各区间的数目。以统计数据落入各区间的频率作为发生概率，以越限区间的中心值做为区间值。设m为数据落入区间的频数，sum为统计期所有节点电压数据的总样本数，则数据落在区间的概率为

1.2 统计指标的定义

1.2.1 5%越限电压最大值指标

1.2.2 95%越限电压期望值指标

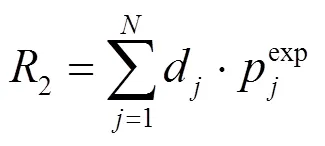
1.2.3 5%越限电压众数值指标

式中，d为5%众数统计落入区间的区间值。

1.3 电压质量越限区间

1.3.1越限电压偏差

越限电压偏差的统计对象为电压偏差超过限值的样本值，定义越限电压偏差为

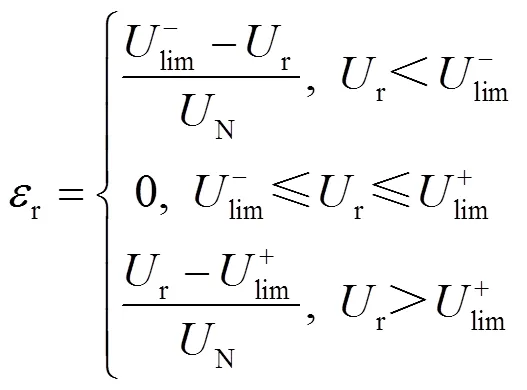
1.3.2越限电压的三相不平衡

利用对称分量法将节点电压有效值进行相序分解，得到节点电压的负序分量及零序分量，并统计电压不平衡超过标准限值的序分量样本。则负序和零序电压不平衡度分别定义为

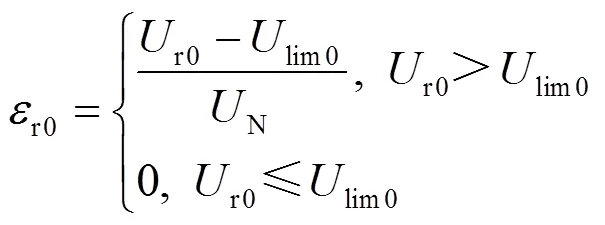
2 光伏接入配电网的分布特征

2.1 分布式光伏渗透率

因配电网自身的功率限制以及电能质量要求，可接入配电网的光伏总容量受到系统的约束。光伏装机容量在配电网中所占比重大小通常采用光伏渗透率来进行表征，定义如式(8)所示。

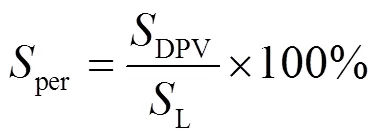
2.2 分布式光伏接入的均匀度

本文从分布式光伏的接入位置、分布状况及单节点渗透率等接入条件考虑，建立分布式光伏接入均匀度指标，如式(9)所示。

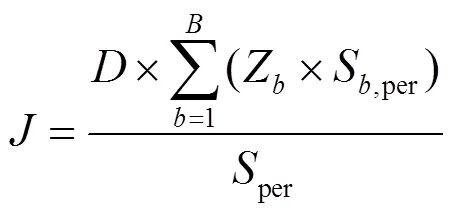
定义单节点光伏渗透率为接入单节点的光伏额定容量及该节点的额定负荷之比，如式(10)所示。

3 光伏接入配电网电压适应性分析

3.1 光伏无功支撑的全局优化调压策略

在各运行优化时段，以全网节点电压偏差之和最小为目标，光伏逆变器无功输出主动支撑调压任务，其无功输出为最优控制量。各时段的全局优化目标函数为

约束条件包括潮流平衡等式约束；不等式约束包括各时段内光伏逆变器无功输出限值、有载调压变压器分接头档位上下限值和各时段内无功补偿电容器最大投切组数。其中，逆变器运行约束为

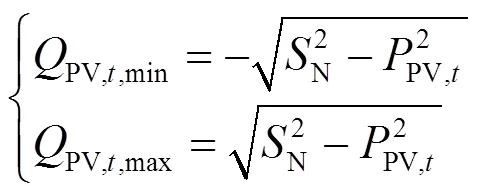
3.2 光伏接入配电网的电压适应性分析

3.2.1 电压偏差及不平衡的适应性

考虑光伏主动支撑调压任务，采用本文提出的电压质量风险评估指标来定量分析在不同光伏渗透率和接入均匀度接入下的配电网电压适应性。为使电压适应度评估结果更能反映电压电能质量的真实状态，在各指标的赋权过程中，不仅需要主观经验，同时也需考虑电压质量的客观实际。因此，本文采用组合赋权法来求取各电压指标权重，并采用AHP- CRITIC组合赋权法来避免AHP法较为强烈的主观性以及CRITIC法忽略指标间的重要程度差异问题[27]。

将电压的95%越限电压期望值指标与5%众数进行组合加权求和，形成各相的电压偏差综合平均指标2。

同理，将5%最大电压不平衡风险指标与标准限值对比得到各相的最大电压不平衡指标，其分别为3,2、3,0。

分别将负序零序电压不平衡的95%期望值与5%众数值指标进行加权求和并归一化处理，得到表征负序零序电压不平衡综合平均指标4。

由上式可知，各指标取值越小则电压质量越好。当指标小于0时，表明配电网电压对光伏接入足以适应；当指标大于0时，表明配电网电压质量难以适应光伏的接入。上述的综合权重通过AHP-CRITIC组合赋权法求得。

3.2.2 AHP-CRITIC线性组合赋权

线性组合赋权法具有简单且灵活性强的优点，可根据实际需求对权值进行调整。因此，在得到主观权重和客观权重之后，采用线性组合赋权进行最终赋权。

对于电压不平衡指标，线性组合赋权得到的95%期望值和众数值电压不平衡风险指标的综合权重为

3.3 配电网电压适应性分析步骤

3.3.1基于历史天气数据构建分析场景

获取待分析地区近年的历史天气数据，采用Kmeans聚类算法对数据序列进行聚类以构建包含太阳辐照度、温度以及负荷的典型场景集合。

日场景集合建立步骤：

1) 确定所构建日场景集合中的典型场景数，将年的光照、温度及负荷历史数据按日划分为数据序列，并对数据序列进行分项处理。

2) 随机选取个日场景数据序列作为初始中心序列；分别计算各数据序列与中心序列间的欧氏距离，并将与中心数据序列最相似的数据聚为一类，并更新迭代出新的中心数据序列。

3) 全部数据序列聚类为个集合则迭代计算完成，将个中心数据序列还原为原始数据作为典型日场景数据。

3.3.2典型场景下电压适应度的随机模拟分析

以1 h为分析步长，运用第4.1节阐述的光伏主动支撑调压策略，基于典型场景，采用随机模拟方法分析光伏不同接入形态下配电网的适应性。

典型场景电压适应度的随机模拟分析步骤：

1) 根据个典型场景中光照、温度数据序列，计算得到各时段内的光伏有功出力值；进而求取各时段内的光伏逆变器无功输出限值。

2) 由各典型场景中负荷数据序列以及1)中计算得到的各分布式光伏有功出力值，结合光伏的接入位置分布，计算各时段内的光伏渗透率和接入分布均匀度指标。

3) 通过粒子群优化算法结合潮流计算得到各光伏逆变器的最优无功输出量，并计算典型场景下的电压偏差指标及各相和各序的电压偏差指标。

4) 每个典型场景代表了若干原始场景，由各典型场景对应的电压偏差及不平衡指标值，可映射得到所代表的原始场景中的各电压指标数据。

5) 由4)得到的原始场景的电压指标数据，计算得到不同光伏渗透率和接入分布均匀度下的电压越限偏差和不平衡指标，进而评估配电网的电压适应性。

4 算例分析

4.1 典型场景集合构建

基于天津市2011—2020年的真实历史天气数据，通过Kmeans聚类得到的55个典型日场景所组成的集合，包括光照以及温度的数据序列，分别如图1所示。

图1 基于Kmeans聚类得到的日场景集合

图1中，典型场景的光照和温度曲线较为分散，且包含了常见的各种天气情况。本文仅以4种典型场景为例来分析，其他场景下分析方法完全相同，所选场景集合如图2所示。

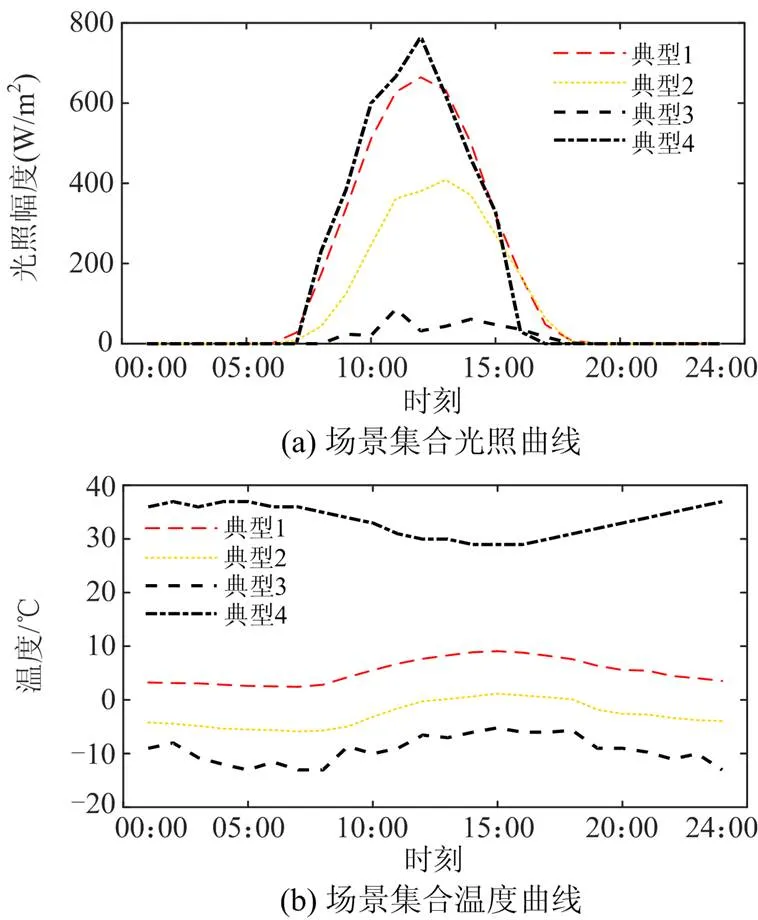
图2 光照及温度的日场景集合

4.2 不同场景下光伏无功调压分析

以IEEE-33配电网模型为例，分布式光伏的接入位置及容量参数如表1所示，设置在节点7、10、13、14、17、20、23处接入三相光伏逆变器，节点26、29、32分别接入单相光伏逆变器，对光伏总并网容量进行平均分配，设置光伏接入均匀度为7.36。各场景下光伏接入配电网且未采取调压措施时各节点电压分布如图3所示。粒子群优化算法的设定参数如表1所示。图3中黄色平面和绿色平面分别表示规定的电压幅值上限和下限。

表1 粒子群算法参数设置

场景1下各时段光伏无功出力的全局优化结果及各日典型场景下配电网各节点电压分别如图4和图5所示。图5中分别用黄色平面和紫色平面表示规定的电压上限和下限。

由图3与图5对比可知，光伏主动支撑的全局调压效果显著，电压越限问题得到解决，且电压分布图形较为平坦。

图4 场景1下分布式光伏无功输出优化结果

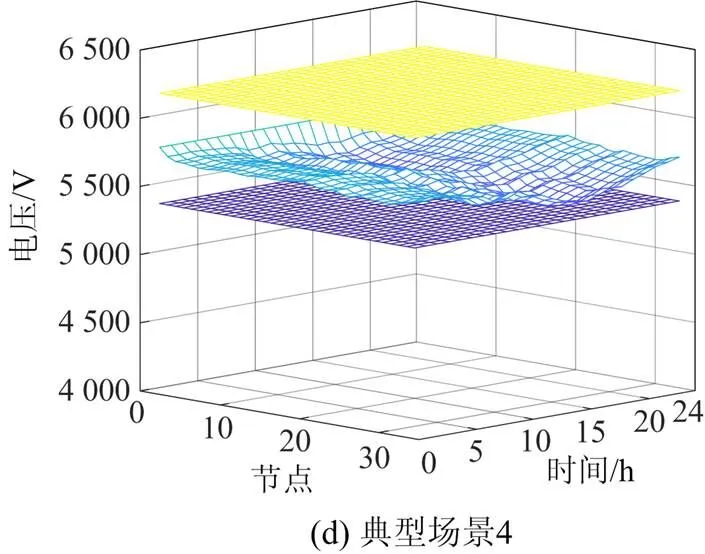
图5 光伏参与的多手段调压结果

4.3 不同光伏渗透率下的电压适应性分析

为探究不同光伏渗透率下配电网电压适应性，采用统计学分析方法。基于各时段内的光伏出力及负荷预测信息，优化分布式光伏用于调压的无功补偿量，得到统计时段内所有节点的电压数据。通过分别增大节点接入光伏容量来模拟光伏渗透率的提高，以一日内13：00为例，得到不同光伏渗透率下的各节点电压幅值如图6所示。

图6中，当光伏渗透率为0%时，节点电压幅值维持在正常范围内。随着光伏渗透率的逐步提高，电压幅值显著提高，当渗透率为70%时，各节点电压基本在电压上限值附近波动，表明光伏接入对电压升高起到了一定的调节作用。而当渗透率达到100%时，大量节点电压越上限，说明光伏本身参与调压仍然会导致电压越限，因此需在一定程度上限制光伏渗透率。

以10%的渗透率为步长，分别对光伏在10%～ 100%渗透率下的电压偏差和不平衡指标进行模拟分析。对于电压综合平均指标，按照AHP-CRITIC组合赋权法对电压风险指标的95%期望值和5%众数值指标进行组合赋权。根据文献[27]中AHP法求得主观权重矩阵1= [0.348 0.652]T。由CRITIC法求得客观权重矩阵2= [0.411 0.589]T。本文参考文献[28]将主观权重系数均设为0.65，客观权重系数均为0.35，则各指标的组合权重为= [0.370 0.630]T。计算得到的配电网不同光伏渗透率下电压偏差和不平衡指标分别如图7和图8所示。

图7中，三相中B相的电压偏差指标较另两相大，说明光伏单相接入导致各相的电压偏差程度存在差异。随着光伏渗透率的逐步提高，5%最大电压偏差指标和综合平均指标均有明显的增大趋势，当渗透率达到90%时，达到一个峰值。与规定的标准限值作比较，5%最大电压偏差指标在光伏渗透率达到70%时大于0，说明此时配电网电压偏差对光伏的接入已不具有适应性。电压偏差综合平均指标在光伏渗透率达到90%时大于0，对光伏接入的包容性更强。

图7 不同光伏渗透率下电压偏差指标

由图8可知，随着分布式光伏渗透率的增加，配电网电压不平衡指标值逐渐增大。从电压最严重指标和平均指标角度来分析适应性角度，配电网电压不平衡指标对光伏接入渗透率的极限分别在85%和100%。

4.4 不同光伏接入均匀度下的电压适应性分析

以光伏渗透率50%为例，将不同容量、不同接入位置的分布式光伏电源分别接于10个节点处。对光伏在不同接入均匀度下的电压指标进行模拟分析，得到不同光伏接入均匀度下的配电网电压偏差和不平衡指标分别如图9和图10所示。

由图9和图10可知，随着光伏接入均匀度的增加，电压偏差和不平衡指标值逐渐减小，说明改变光伏接入均匀度能够改善配电网节点电压的整体分布。图9(b)可得出，当光伏渗透率为50%时，在不同的光伏接入均匀度下，配电网电压偏差对光伏接入均能适应。从图10可知，负序不平衡较零序更为严重。当均匀度大于4时，配电网电压不平衡对光伏接入足以适应。

5 结论

本文在光伏高比例接入且具有无功支撑作用背景下，研究配电网接纳高比例光伏的电压适应性分析方法。采用统计分析手段分别建立节点电压偏差和不平衡统计学指标，从节点电压的5%最大值指标和综合平均指标两方面反映配电网对光伏接入的适应性。建立光伏渗透率和接入均匀度指标以表征分布式光伏的接入形态。基于天气数据驱动手段构建了典型场景的随机模拟，定量分析了配电网对光伏不同渗透率和接入均匀度下的电压适应性。结果表明，考虑光伏主动支撑配电网调压任务，在一定的光伏渗透率范围内，配电网电压对光伏渗透率的增加是可适应的，在本文研究中存在峰值。随着光伏接入均匀度的提高，配电网对光伏接入的适应性增强。本文研究可为光伏高比例接入配电网的规划提供分析手段和一定的指导建议。

[1] 张敏, 刘进, 林江刚, 等.“双碳”背景下屋顶分布式光伏开发环境效益分析[J]. 能源研究与利用, 2021(6): 37-41.

ZHANG Min, LIU Jin, LIN Jianggang, et al. Environmental benefit analysis of rooftop distributed photovoltaic development under the background of "double carbon"[J]. Energy Research and Utilization, 2021(6): 37-41.

[2] 王文宾, 朱燕舞, 韩天华, 等. 基于随机规划的分布式光伏并网最大准入容量计算[J]. 燕山大学学报, 2018, 42(6): 510-518.

WANG Wenbin, ZHU Yanwu, HAN Tianhua, et al. Maximum access capacity calculation of distributed PV grid connected based on stochastic programming[J]. Journal of Yanshan University, 2018, 42(6): 510-518.

[3] 李晓明, 刘翔宇, 李安昌, 等. 配电网电压控制的分布式光伏无功仿射可调鲁棒优化方法[J]. 电力系统保护与控制, 2021, 49(12): 124-131.

LI Xiaoming, LIU Xiangyu, LI Anchang, et al. Distributed photovoltaic reactive power affine adjustable robust optimization method for voltage control of a distribution network[J]. Power System Protection and Control, 2021, 49(12): 124-131.

[4] LEÓN L F, MARTINEZ M, ONTIVEROS L J, et al. Devices and control strategies for voltage regulation under influence of photovoltaic distributed generation: a review[J]. IEEE Latin America Transactions, 2022, 20(5): 731-745.

[5] 王景钢, 刘轶. 考虑光伏逆变器电流裕度的主动配电网动态电压支撑策略[J]. 电力系统保护与控制, 2021, 49(6): 105-113.

WANG Jinggang, LIU Yi. Dynamic voltage support strategy for an active distribution network considering the current margin of a photovoltaic inverter[J]. Power System Protection and Control, 2021, 49(6): 105-113.

[6] 王超洋, 张蓝宇, 刘铮, 等. 基于特征挖掘的indRNN光伏发电功率预测[J]. 电力系统及其自动化学报, 2021, 33(4): 17-22.

WANG Chaoyang, ZHANG Lanyu, LIU Zheng, et al. Feature mining based indRNN photovoltaic power generation prediction[J]. Proceedings of the CSU-EPSA, 2021, 33(4): 17-22.

[7] CALLEGARO L, ROJAS C A, CIOBOTARU M, et al. A controller improving photovoltaic voltage regulation in the single-stage single-phase inverter[J]. IEEE Transactions on Power Electronics, 2022, 37(1): 354-363.

[8] 靳伟, 王文宾, 陈岩, 等. 计及分布式光伏有功削减的配电网全局电压综合优化策略[J]. 燕山大学学报, 2020, 44(2): 164-172.

JIN Wei, WANG Wenbin, CHEN Yan, et al. Global voltage comprehensive optimization strategy for distribution network considering distributed photovoltaic power reduction[J]. Journal of Yanshan University, 2020, 44(2): 164-172.

[9] 肖浩, 裴玮, 邓卫, 等. 分布式电源对配电网电压的影响分析及其优化控制策略[J]. 电工技术学报, 2016, 31(增刊1): 203-213.

XIAO Hao, PEI Wei, DENG Wei, et al. Analysis of the impact of distributed generation on distribution network voltage and its optimal control strategy[J]. Transactions of China Electrotechnical Society, 2016, 31(S1): 203-213.

[10] LI Y, SUN Y, LI K, et al. Analysis and suppression of voltage violation and fluctuation with distributed photovoltaic integration[J]. Symmetry, 2021, 13(10): 1894.

[11]颜湘武, 徐韵. 考虑网络动态重构含多异质可再生分布式电源参与调控的配电网多时空尺度无功优化[J].电工技术学报, 2019, 34(20): 4358-4372.

YAN Xiangwu, XU Yun. Multiple time and space scale reactive power optimization for distribution network with multi-heterogeneous RDG participating in regulation and considering network dynamic reconfiguration[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4358-4372.

[12]李建芳, 张璐, 宋晓辉, 等. 含高渗透率分布式电源的配电网多目标无功分区及主导节点选择方法[J]. 可再生能源, 2017, 35(11): 1664-1671.

LI Jianfang, ZHANG Lu, SONG Xiaohui, et al. Multi- objective reactive power partitioning and pilot node selection of distribution network with high penetration of DG[J]. Renewable Energy Resources, 2017, 35(11): 1664-1671.

[13] ABRI R A, EL-SAADANY E F, ATWA Y M. Optimal placement and sizing method to improve the voltage stability margin in a distribution system using distributed generation[J]. IEEE Transactions on Power Systems, 2013, 28(1): 326-334.

[14]倪爽, 崔承刚, 郑庆荣, 等. 基于多风电相关性场景生成法的配电网随机多目标无功优化[J]. 浙江电力, 2020, 39(11): 103-111.

NI Shuang, CUI Chenggang, ZHENG Qingrong, et al. Stochastic multi-objective reactive power optimization of distribution network based on multiple wind turbines correlative scenario generation method[J]. Zhejiang Electric Power, 2020, 39(11): 103-111.

[15] CHAI Y, GUO L, WANG C, et al. Network partition and voltage coordination control for distribution networks with high penetration of distributed PV units[J]. Transactions on Power Systems, 2022, 33(3): 3396-3407.

[16] ZHAO B, XU Z, XU C, et al. Network partition-based zonal voltage control for distribution networks with distributed PV systems[J]. IEEE Transactions on Smart Grid, 2017, 9(5): 4087-4098.

[17] EMARATI M, BARANI M, FARAHMAND H, et al. A two-level over-voltage control strategy in distribution networks with high PV penetration[J]. International Journal of Electrical Power & Energy Systems, 2021, 130.

[18]张艳萍, 郭成. 分布式光伏并网对配电网的影响研究[J]. 云南电力技术, 2021, 49(1): 38-43.

ZHANG Yanping, GUO Cheng. Review on the influence of distributed photovoltaic grid connection on distribution network[J]. Yunnan Electric Power, 2021, 49(1): 38-43.

[19]吴斌, 单来支, 王庆, 等. 基于三相不平衡的分布式光伏接入配电网的优化配置研究[J]. 电力系统保护与控制, 2019, 47(24): 108-114.

WU Bin, SHAN Laizhi, WANG Qing, et al. Research on optimal configuration of distributed photovoltaic access distribution network based on three-phase unbalance[J]. Power System Protection and Control, 2019, 47(24): 108-114.

[20] VIEIRA R, GUERRA M I, BANDEIRA S. Analysis of the power quality of a grid-connected photovoltaic system[J]. IEEE Latin America Transactions, 2020, 18(4): 714-721.

[21] MAHELA O P, KHAN B, ALHELOU H H, et al. Power quality assessment and event detection in distribution network with wind energy penetration using stockwell transform and fuzzy clustering[J]. IEEE Transactions on Industrial Informatics, 2020, 16(11): 6922-6932.

[22] 毛锐, 袁康龙, 钟杰峰, 等. 基于概率潮流法的含分布式光伏的配电网电压状态评估[J]. 电力系统保护与控制, 2019, 47(2): 123-130.

MAO Rui, YUAN Kanglong, ZHONG Jiefeng, et al. Distribution network voltage state assessment with distributed generation based on probabilistic power flow method[J]. Power System Protection and Control, 2019, 47(2): 123-130.

[23] 张艳萍, 郭成, 尹轲. 一类低压配电网过电压原因分析及评判方法研究[J]. 浙江电力, 2021, 40(5): 112-118.

ZHANG Yanping, GUO Cheng, YIN Ke. Cause analysis and evaluation method of a type of overvoltage in low-voltage distribution networks[J]. Zhejiang Electric Power, 2021, 40(5): 112-118.

[24] 刘颖英, 冯丹丹, 林才华, 等. 电能质量综合评估研究现状及发展趋势[J]. 电力系统保护与控制, 2020, 48(4): 167-176.

LIU Yingying, FENG Dandan, LIN Caihua, et al. Current status and development trend of power quality comprehensive assessment[J]. Power System Protection and Control, 2020, 48(4): 167-176.

[25] 电能质量—三相电压不平衡: GB/T 15543—2008[S]. 北京: 中国电力出版社, 2008.

Power quality—three-phase voltage unbalance: GB/T 15543—2008[S]. Beijing: China Electric Power Press, 2008.

[26] 电能质量—供电电压偏差: GB/T 12325—2008[S]. 北京: 中国电力出版社, 2008.

Power quality—power quality deviation of supply voltage: GB/T 12325—2008[S]. Beijing: China Electric Power Press, 2008.

[27]王小雷, 宋耐超, 史雷敏, 等. 基于边缘计算的台区状态综合评价方法[J/OL].电测与仪表: 1-8[2021-12-16]. http://kns.cnki.net/kcms/detail/23.1202.TH.20210525. 1231.003.html.

WANG Xiaolei, SONG Naichao, SHI Leimin, et al. Comprehensive evaluation method of transformer area status based on edge computing[J/OL]. Electrical Measurement & Instrumentation: 1-8[2021-12-16]. http:// kns.cnki.net/kcms/detail/23.1202.TH.20210525.1231.003. html.

[28]肖白, 李攀攀, 姜卓, 等. 基于梯级组合评分的农村电网精益化改造方法[J]. 电力系统自动化, 2020, 44(3): 220-230.

XIAO Bai, LI Panpan, JIANG Zhuo, et al. Lean transformation method for rural power grid based on cascade combination score[J]. Automation of Electric Power Systems, 2020, 44(3): 220-230.

Voltage adaptability of distributed photovoltaic access to a distribution network considering reactive power support

LI Zheng1, WANG Wenbin1, HAN Shengfeng1, LIN Lijuan2

(1. Xingtai Power Supply Branch, State Grid Hebei Electric Power Co., Ltd., Xingtai 054001, China; 2. Key Lab of Power Electronics for Energy Conservation and Motor Drive of Hebei Province, Yanshan University, Qinhuangdao 066004, China)

New power systems will be built with ‘new’ energy as the main component. Distributed photovoltaics are the main trend in high proportion penetration. The fluctuation of photovoltaic output is prone to cause voltage out of limit and three-phase imbalance of a distribution network. The residual capacity of a photovoltaic inverter has the function of voltage active support, which is conducive to improving voltage quality. At the same time, the large resistance inductance ratio of a distribution network makes the coupling between voltage and active power obvious, resulting in the comprehensive influence of photovoltaic active and reactive power on the voltage of the network. This paper studies the carrying capacity of the network in accepting three-phase and single-phase distributed photovoltaics from the perspective of voltage adaptability. First, according to statistical principles, the indices reflecting the voltage quality statistical characteristics of maximum value, expected value and public value are established. The access characteristics of distributed photovoltaic are described from the two aspects of photovoltaic permeability and the dispersion of access location. Secondly, a typical daily scenario is constructed based on historical weather data, considering the active participation of photovoltaic in voltage support, and the statistical indicators of voltage quality of each node are obtained by random simulation analysis. Finally, the AHP-CRITIC combination weighting method is used to combine the statistical indices of voltage deviation and imbalance, and the comprehensive indices representing voltage adaptability are obtained. An example is analyzed using OpenDSS software, and the results verify the effectiveness of the method.

distribution network; distributed photovoltaic; active support; scenario construction; voltage adaptability

10.19783/j.cnki.pspc.211781

国家自然科学基金项目资助(51807172)；国网河北省电力有限公司科技项目资助(kj2021-041)

This work is supported by the National Natural Science Foundation of China (No. 51807172).

2021-12-30；

2022-02-16

李 征(1983—)，男，硕士，高级工程师，研究方向为新能源电力系统运行控制；E-mail: xtlizheng@126.com

林丽娟(1991—)，女，通信作者，博士研究生，研究方向为配电网电能质量分析与治理。E-mail: linlijuan19324@ 163.com

(编辑 张爱琴)