逆变电源对风火/光火打捆送端电网低频振荡影响及其惯量匹配方法
王 倩,盛四清,田颢璟
逆变电源对风火/光火打捆送端电网低频振荡影响及其惯量匹配方法
王 倩,盛四清,田颢璟
(华北电力大学电气与电子工程学院,河北 保定 071003)
为研究逆变电源(Inv)对“风火/光火”打捆送端电网稳定运行的影响,提出了一种计及系统参数的控制模型及不同类型电源的惯量匹配方法。首先,构建Inv所有控制环节的数学模型,进而形成整个研究系统的小信号模型,并通过Matlab仿真验证。其次,基于小信号模型利用根轨迹法,分析系统参数对送端电网内部低频振荡的影响。研究表明送端电网内部线路越短,阻感比越大,Inv出力越多,越有利于系统稳定。最后,利用等效电源原理,推导出送端电网中两种类型电源的惯量匹配方法。RT-LAB半实物仿真验证了所提惯量匹配公式能更好分配功率,提高送端电网稳定性。
逆变电源;送端电网;小信号模型;低频振荡;惯量匹配
0 引言
近年来,随着能源互联战略的实施,系统中新能源渗透率不断提高[1-5]。与传统同步电源不同,以风电和光伏为主要代表的逆变电源多通过电力电子设备接入系统,这类电源因其弱惯性和低阻尼性,大量接入后将影响系统的动态响应和稳定性[6-9]。
为此,国内外学者提出了针对Inv的虚拟惯量控制、一次调频控制和阻尼控制等多种方法[10-11],与此同时,国标对不同Inv并网条件提出相关要求[12-13]。考虑到Inv通常“与同步电源打捆”的形式接入到送端电网[14],其对送端电网区域内低频振荡特性以及系统稳定性的影响也日益受到重视[15]。
目前针对Inv的研究工作主要集中在稳定性分析和影响原因分析两个方面。
稳定性分析:文献[16]针对电压控制型Inv和电流控制型Inv参与大电网控制的情况,分别分析了改变其控制环节参数对系统稳定性的影响。指出过小的有功调频系数f,会导致含有电压控制型Inv的系统由于新引入的模态阻尼小于零而使系统失稳。同时指出过大的惯性时间常数j会导致含有电流控制型Inv系统的高频模态阻尼小于零,系统将引发高频振荡失稳。文献[17]通过小信号理论分析得出,在微电网中,有功、无功下垂系数,转动惯量和虚拟电阻增大,都会导致低频特征根阻尼比降低,不利于系统稳定。文献[18]分析得出,在单机无穷大系统中,当虚拟电阻或者虚拟电感过大时,系统可能出现低频振荡。但是以上分析都是针对接入无穷大系统或者微电网中Inv本身参数对系统稳定性的影响,不适用于“风火/光火”打捆送出系统,并且未考虑送端电网其他参数对系统稳定性影响。
影响原因分析:文献[19]通过分析特征根对系统各参数的影响效果,针对不同参数对特征根的影响程度进行解释。文献[20]认为Inv一次调频响应时间会影响状态变量参与因子,进而影响Inv参数对特征根的影响程度,响应时间越短,向系统提供的低频阻尼越强,越有利于系统稳定。文献[21]建立了考虑Inv影响的送出系统等效转子运动方程模型,研究了Inv一次调频与虚拟惯量控制对系统低频振荡特性的影响机理,指出Inv会影响其公用输电通道的SG电磁功率,进而影响系统阻尼。但是以上分析均着眼于稳态时有功功率,忽略了无功功率以及负荷波动时Inv和SG响应速度差异对稳定性的影响。
本文针对上述问题,首先建立Inv模型,通过系统小信号模型求解并辨识“风火/光火”送出电网区域内低频特征根;其次分析惯性时间常数、有功调频系数、内部线路参数以及Inv出力占比等参数变化时对低频特征根以及系统稳定性的影响情况;最后提出了Inv惯量整定表达式,并通过RT-LAB半实物仿真平台验证其有效性。
1 系统小信号建模
本文研究的“风火/光火”打捆送出系统如图1所示,具体如下:送端电网主要包含SG1和Inv2,其中,SG1直接连接到送端电网并网点(PCC1),Inv2通过内部线路接到PCC1。受端电网主要包含SG3和负荷,两者直接连接到受端电网并网点(PCC2),送端和受端电网经过200 km的220 kV架空线连接。
Inv2结构如图2所示,通过有功功率控制、无功功率控制、虚拟阻抗控制、内环控制环节生成调制波,经过脉冲宽度调制(Pulse Width Modulation, PWM)产生驱动信号驱动Inv2开关器件的开断。
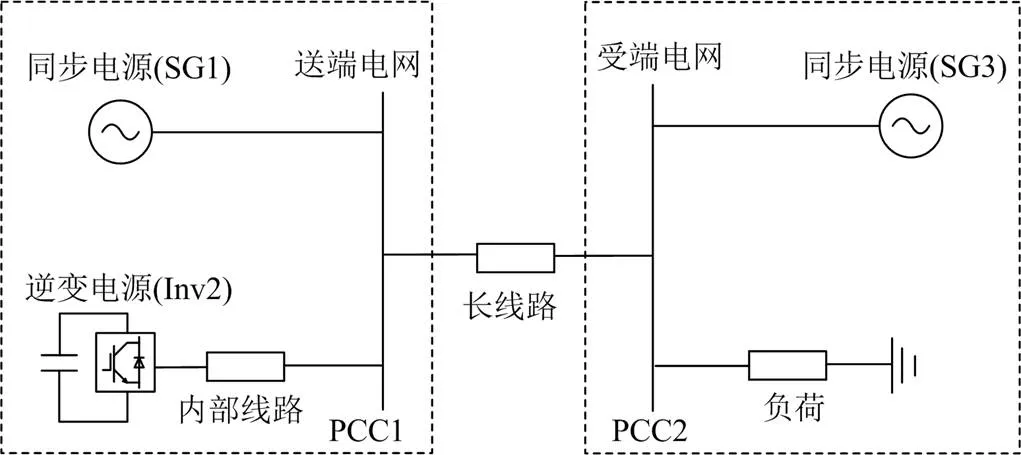
图1 “风火/光火”打捆送出系统

图2 逆变电源控制器结构
1.1 SG状态方程
同步电源的二阶经典数学模型描述了其转子运动方程的基本特性,忽略了复杂的电磁暂态过程,适用于研究低频振荡问题。因此本文采用SG的二阶模型开展研究[18]。
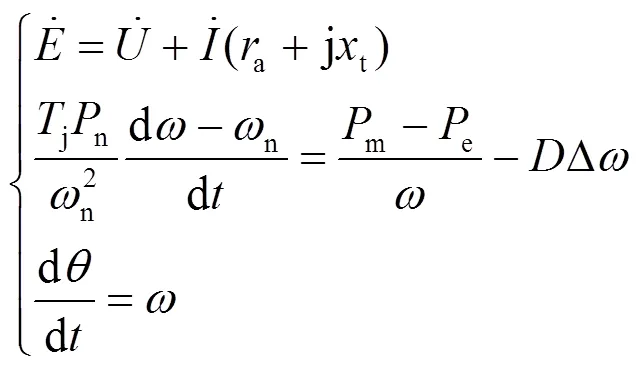
本节关于送端电网中SG1和受端电网中SG3的有功功率控制环节、无功功率控制环节、功率测量与计算环节的状态方程可参考文献[19]。
1.2 内部线路状态方程
如图1所示,Inv2通过内部线路连接到PCC1,其状态方程可表示为
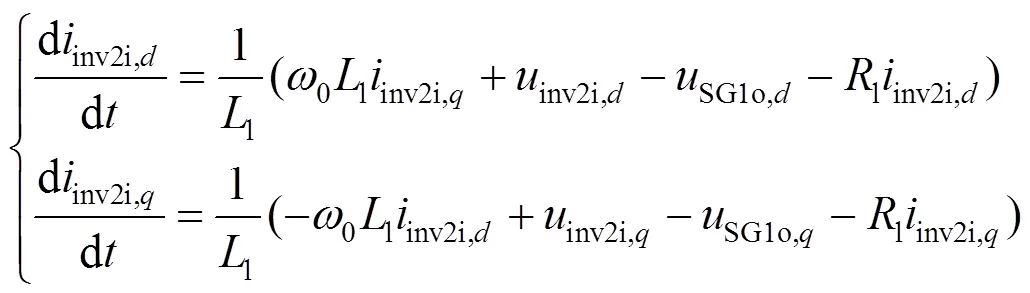
1.3 长线路状态方程
如图1所示,送端电网和受端电网通过长线路连接,其状态方程为
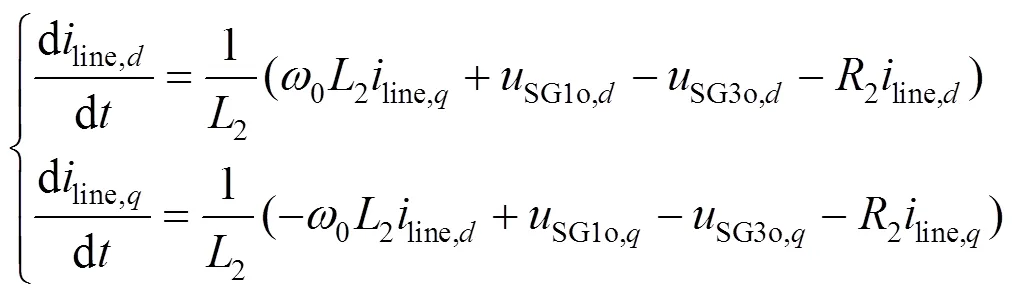
1.4 负荷状态方程
系统中的大多数负荷是异步电动机,呈现阻感特性,受端电网用RL的等值负荷代替所建系统的用电负荷。R、L负荷对应的状态方程为
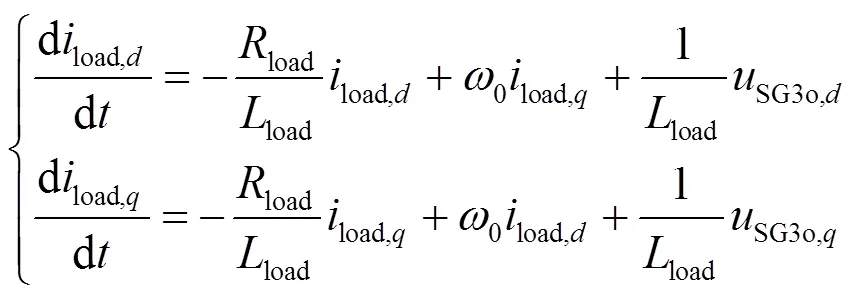
1.5 有功功率控制环节状态方程
图2中的有功功率控制环节所对应的状态方程可表示为
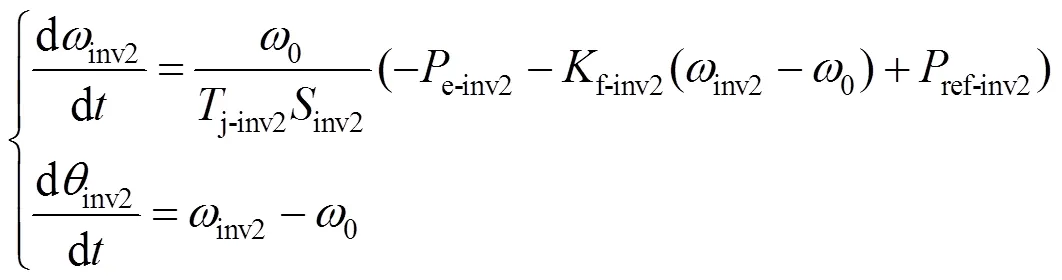
1.6 无功功率控制环节状态方程
图2中的无功功率控制环节对应的状态方程如式(6)所示。
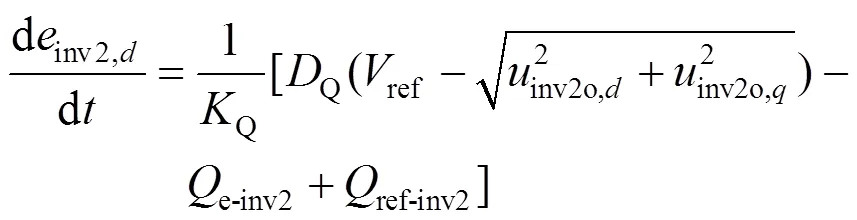
1.7 虚拟阻抗控制环节状态方程
图2中的虚拟阻抗控制环节所对应的状态方程可表示为
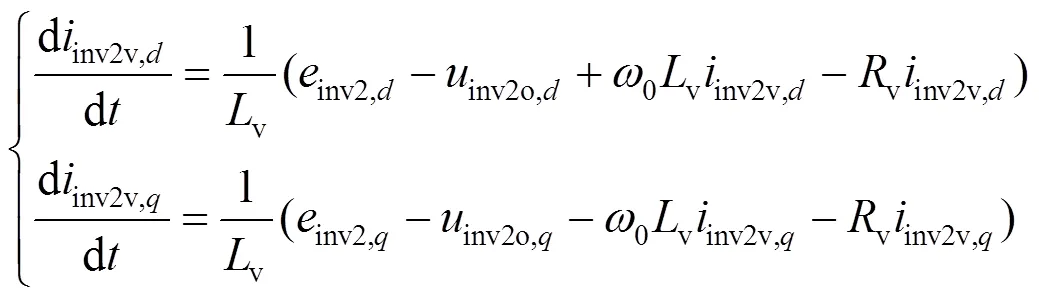
1.8 内环控制环节状态方程
图2中的内环控制环节对应的状态方程可表示为

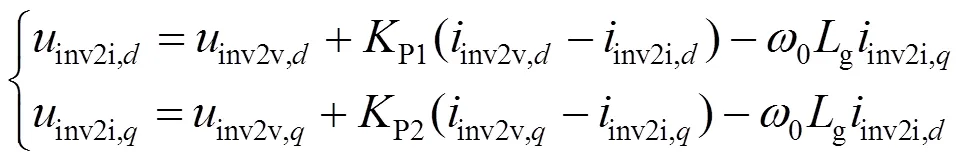
1.9 系统小信号建模及验证
联立式(2)—式(9),可求解系统稳态运行点,在稳态运行点进行线性化,系统的小信号模型如式(10)所示[22-23]。

式中:Δ= [ΔSG1i,d, ΔSG1i,q, ΔSG1, ΔSG1, ΔSG1i,d, Δe-SG1, Δe-SG1, Δinv2i,d, Δinv2i,q, Δinv2o,d, Δinv2o,q, Δinv2o,d, Δinv2o,q, Δinv2, Δinv2, Δinv2,d, Δinv2v,d, Δinv2v,d, Δinv2v,q, Δinv2v,q, Δe-inv2, Δe-inv2, ΔSG1i,d, ΔSgi1,q, ΔSG3, ΔSG3, ΔSG3i,d, Δe-SG3, Δe-SG3, Δload,d, Δload,q]T为系统状态量;为系统的状态矩阵,为系统的输入矩阵;Δ表示相应状态变量可以进行线性化的微小变化状态。其中SG1i,d和SG1i,q分别为SG1输出电流的轴和轴分量,SG和SG分别SG角速度和电动势角度,e-SG和e-SG分别同步电源输出的有功功率和无功功率。
为验证以上所推导小信号模型的正确性,在Matlab/Simulink中建立与小信号模型对应的数字仿真模型进行对比验证。小信号模型和Simulink模型的参数如表1所示。
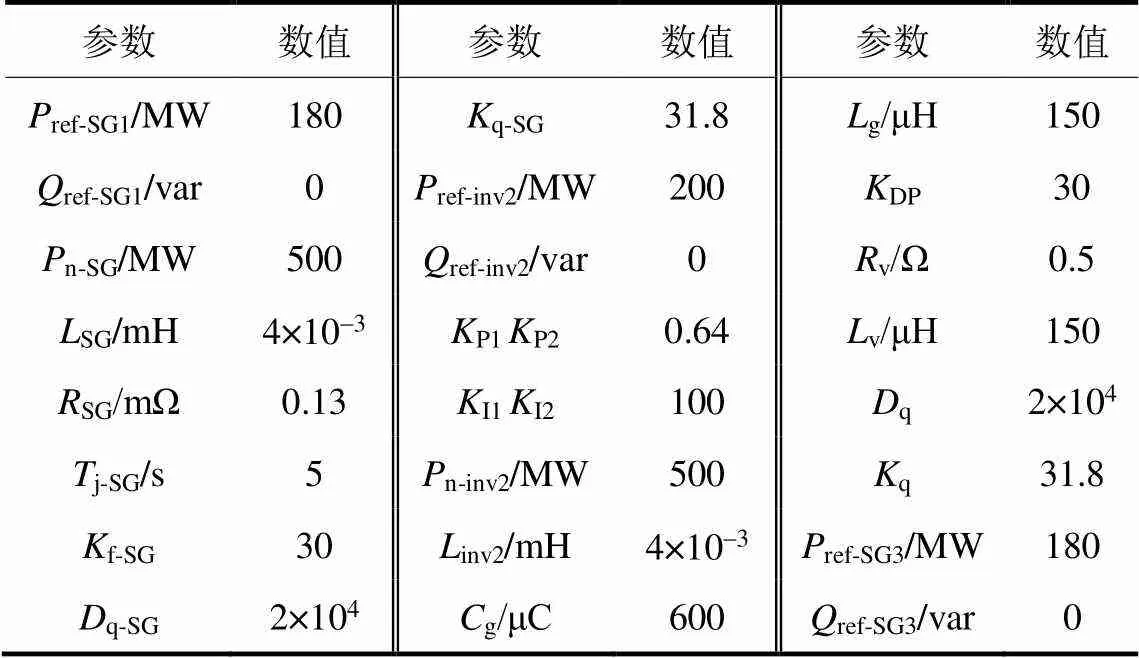
表1 系统主要参数
对比Inv2有功参考值ref-inv2阶跃1 MW时,两个模型得出的Inv2输出有功功率和角速度的动态变化过程,如图3所示。从图3可以看出,小信号数学模型与Matlab/Simulink仿真模型对应的系统动态曲线基本吻合,可以证明小信号模型的正确性。

图3 对比Simulink仿真模型与小信号模型
2 “风火/光火”送端电网低频振荡分析
通过式(11),得到图1所示整体系统的小信号模型,根据表1所示系统的主要参数可以计算系统的特征根以及影响特征根的主要相关变量,结果如表2所示(计算结果已经归一化处理)。
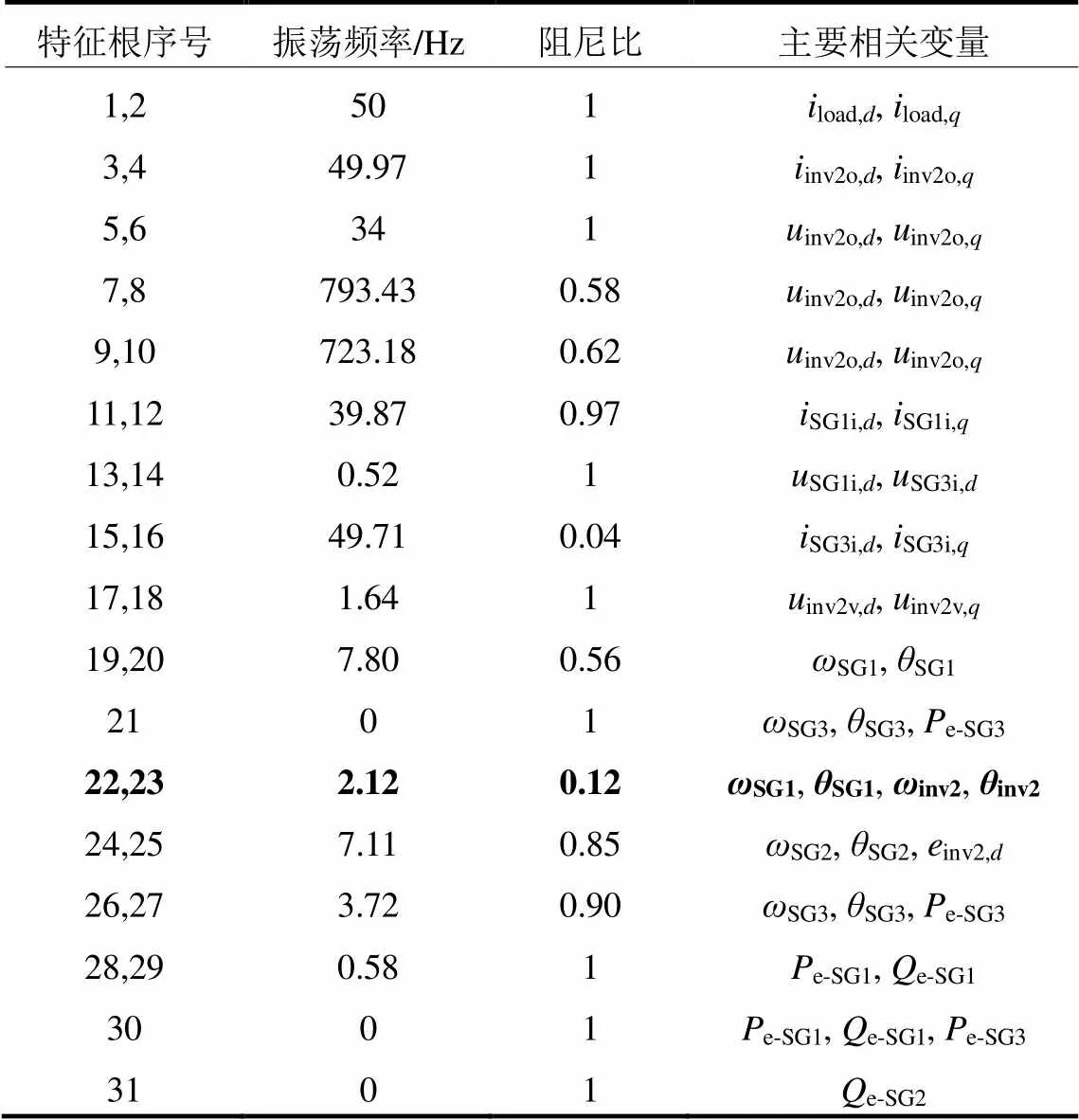
表2 系统特征根特性
由表2可知,系统的31个特征根的阻尼比均大于零,系统是小干扰稳定的。低频振荡模态对应的振荡频率一般为0.2~2.5 Hz[20],再结合主要相关变量,可以确定特征根中22-23对应振荡模态为“风火/光火”送端电网区域内的低频振荡模态,后文着重分析送端电网参数对22-23的影响。
2.1 惯性时间常数对低频特性的影响
由于逆变电源参数的可控性,Inv2的惯性时间常数可以在一定范围内调节。而同步电源参数一般不可调节,但是不同类型同步电源的惯性时间常数存在差异,本节用不同惯性时间常数研究不同同步电源对“风火/光火”送端电网区域内的低频振荡特性的影响,2.2节类似。
当SG1的惯性时间常数j-SG1= 3→7,Inv2的惯性时间常数j-inv2= 5时,低频特征根22-23的变化轨迹如图4(a)所示;当j-SG1= 5,j-inv2= 3→7时,时低频特征根22-23的变化轨迹如图4(b)所示。
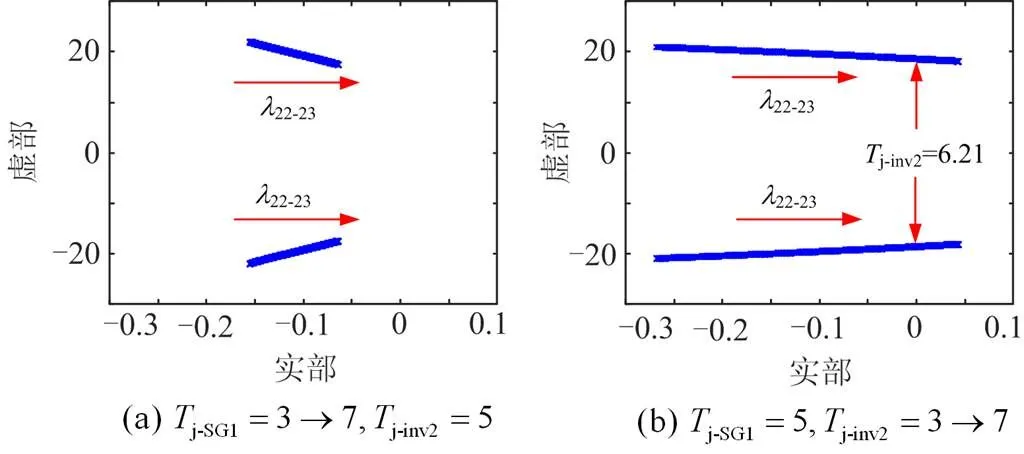
图4 惯性时间常数对特征根的影响
由图4可知,无论SG1还是Inv2,增大j-SG1或者j-inv2都会使送端电网的区域内低频振荡模态对应特征根均向右移动,对应的振荡频率减小,阻尼减小,不利于系统稳定。但当j-SG1= 3→7时,22-23实部变化绝对值为0.091,且恒小于零,系统始终保持稳定;当j-inv2= 3→7时,22-23实部变化绝对值为0.311,当j-inv2大于6.21时,22-23实部大于零,系统失稳。并且相比于j-SG1,j-inv2对22-23的影响更明显。
2.2 有功调频系数对低频特性的影响
当SG1的有功调频系数f-SG1= 30→10,Inv2的有功调频系数f-inv2= 30时,低频特征根22-23的变化轨迹如图5(a)所示;f-SG1= 30,f-inv2= 30→10低频特征根22-23的变化轨迹如图5(b)所示。
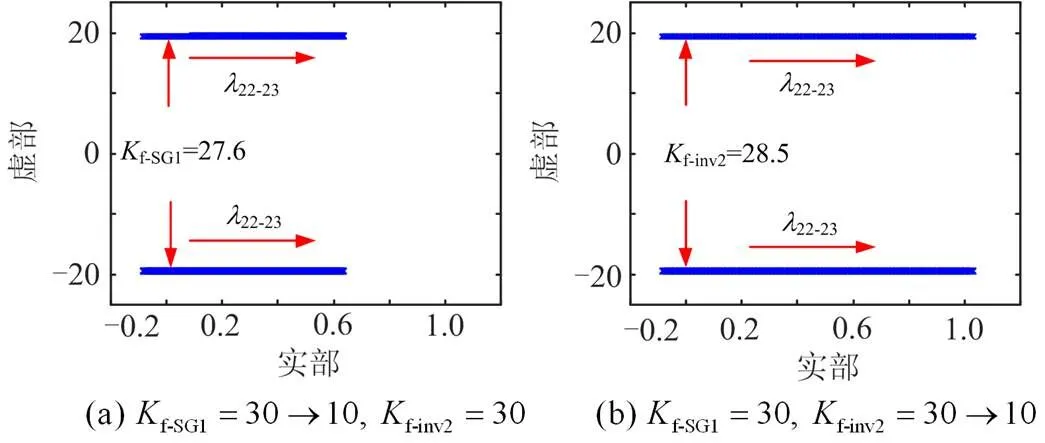
图5 有功调频系数对特征根的影响
如图5所示,无论SG1还是Inv2,减小f-SG1或者f-inv2都会使送端电网区域内低频振荡模态对应特征根向右下方移动,对应的振荡频率基本不变,阻尼减小,不利于系统稳定。但是当f-SG1= 30→10时,22-23实部变化绝对值为0.719,且当f-SG1小于27.6时,特征根实部大于零,系统失稳;当f-inv2= 30→10时,22-23实部变化绝对值为1.111,且当f-inv2小于28.5时,22-23实部大于零,系统失稳。并且相比于f-SG1,f-inv2对22-23的影响更明显,与2.1节结论类似。
2.3 内部线路参数对低频特性的影响
内部线路阻感性质可能会影响有功频率、无功电压的解耦下垂控制,进而影响送端电网区域内低频振荡特性。内部线路的阻感比(1/1)从15变化到0.01,22-23的变化轨迹如图6所示。
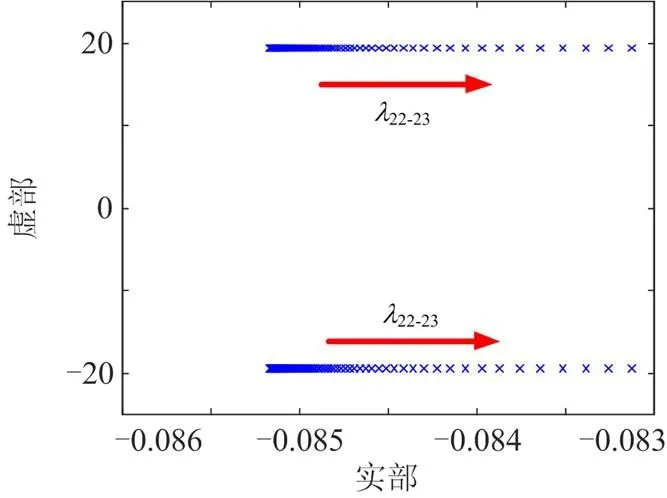
图6 阻感比对特征根的影响
当线路阻抗模值不变,线路从阻性变为感性时,22-23向右移动,不利于系统稳定,即可认为线路的电阻特性会提供正阻尼作用,抑制系统低频振荡。
为了分析内部线路长度(1)对送端电网区域内低频振荡特性的影响,分析内部线路从10 m到1 km时,22-23的变化轨迹如图7所示。
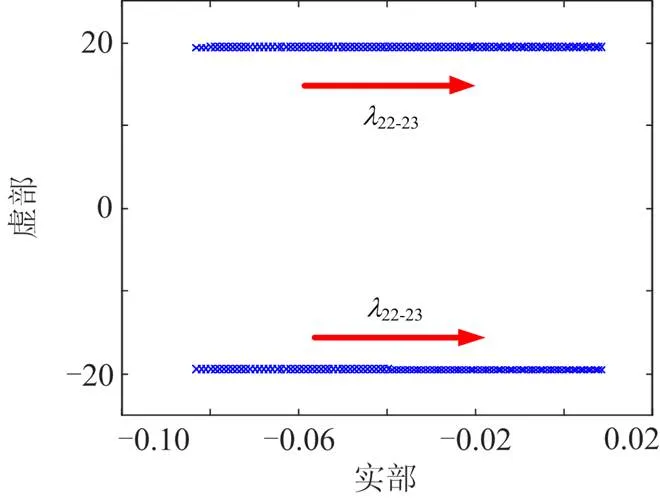
图7 线路长度对特征根的影响
当内部线路阻感比不变,仅增加内部线路长度时,22-23向右移动,系统阻尼比变小,不利于系统稳定,当线路大于890 m时,系统失稳。随着内部线路增加,Inv2与SG1之间电气联系变弱,送端电网区域内部更容易出现低频振荡。
2.4 逆变电源出力对低频特性的影响
在送端电网总出力保持在200 MW的前提下,分析Inv2出力占比(w)从0变化到30%时,22-23的变化轨迹,如图8所示。
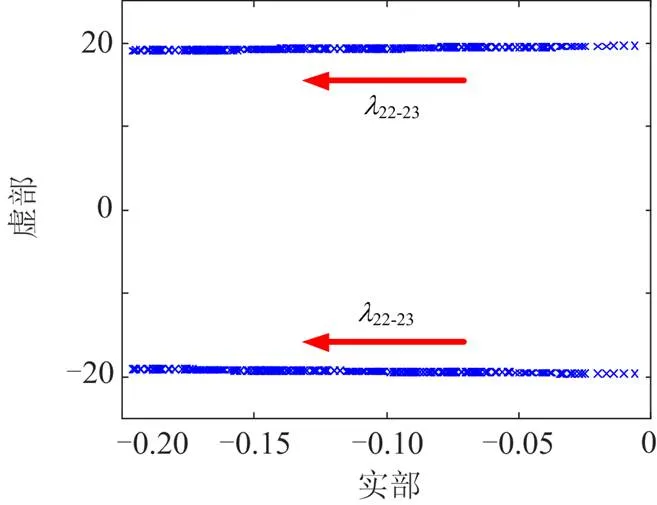
图8 αw对特征根的影响
随着w的增加,22-23向左移,阻尼比增加,有利于系统稳定,Inv2的控制参数可以为低频振荡模态提供阻尼,这也说明本文对Inv2建模方法的有效性。
2.5 仿真验证
为验证上述小信号稳定性分析的相关结论,利用RT-LAB进行半实物仿真实验,搭建与小信号系统一致的RT-LAB测试系统,测试系统参数与小信号模型保持一致,采用表1的参数。
在RT-LAB测试系统中开展对应测试,测试操作时序如下:在测试第0 s时于受端投入40 MW有功负荷,并在0~20 s设置j-inv2= 3,f-inv2= 30;在第20 s切除受端40 MW的有功负荷,并在20~40 s设置j-inv2= 5,f-inv2= 30;在仿真第40 s于受端再次投入40 MW有功负荷,并在40~60 s设置j-inv2= 3,f-inv2= 29;在第60 s再次切除受端40 MW的有功负荷,并在60~80 s设置j-inv2= 5,f-inv2= 29。内部线路功率振荡结果如图9所示。

图9 Inv2参数对低频振荡影响的RT-LAB测试结果
对图9所示结果进行Prony分析,结果如表3所示,其中为Prony分析所得低频振荡阻尼比。如表3所示,当f-inv2= 30、j-inv2= 3时,低频阻尼比= 7.9,当f-inv2= 30、j-inv2= 5,低频阻尼比= 6.2,可以验证“Inv2的惯性时间常数j-inv2增大不利于系统稳定”的结论。当f-inv2= 30、j-inv2= 5,低频阻尼比= 6.2、f-inv2= 29、j-inv2= 5,低频阻尼比= 6.12,可以验证“Inv2的有功调频系数f-inv2减小不利于系统稳定”的结论。

表3 Inv2参数对低频振荡影响的RT-LAB结果Prony分析
分别设置不同的内部线路阻感比(1/1)、内部线路长度(1)以及逆变电源出力(w),通过RT-LAB半实物仿真平台,观察内部线路上功率振荡情况,并进行Prony分析,结果如表4所示。
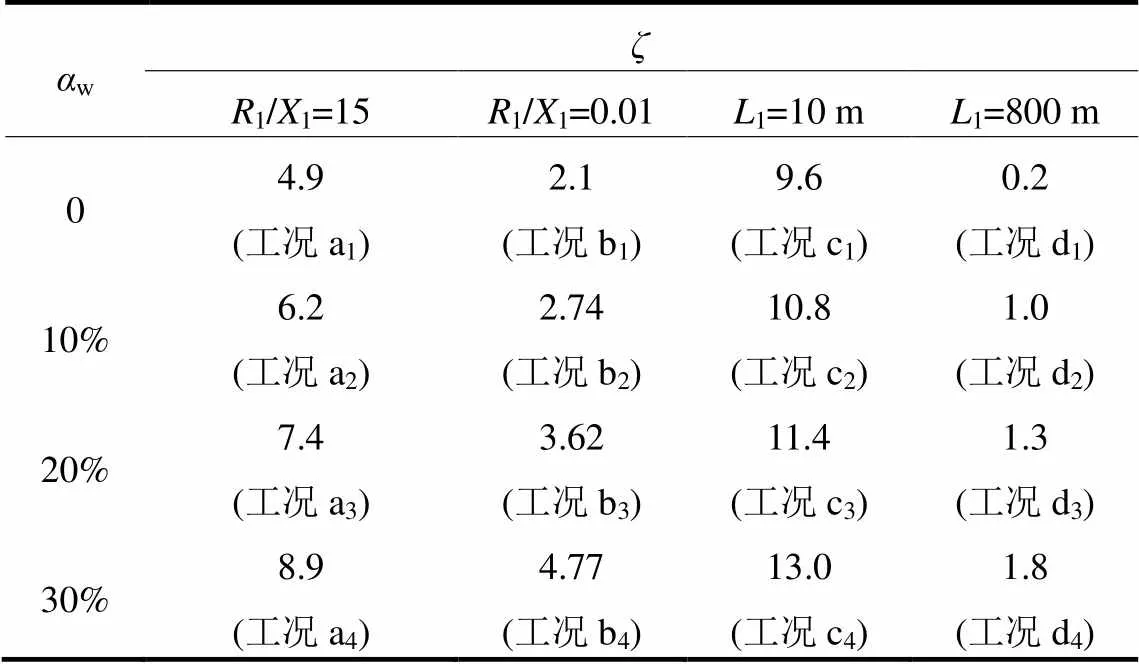
表4 R1/X1 , L1和αw对低频振荡影响的Prony分析
如表4所示,通过a1、a2、a3、a4四个工况与b1、b2、b3、b4四个工况对比,可以验证“内部线路由阻性变为感性,不利于系统稳定”的结论。通过c1、c2、c3、c4四个工况与d1、d2、d3、d4四个工况对比,可以验证“内部线路长度增大,不利于系统稳定”的结论。通过对比a1、a2、a3、a4四个工况可以验证“逆变电源出力增加,有利于系统稳定”的结论。
3 逆变电源惯量匹配方法
在“风火/光火”打捆的送端电网中,当系统的总负荷发生变化时对应系统的频率改变,如果各发电单元的有功调频过渡过程存在时间上的差异,必定影响“风火/光火”打捆中并列运行的各个发电单元的同期性和一致性;本节将重点分析在“风火/光火”打捆送端电网中整定逆变电源的惯性时间常数,使得整个系统的频率过渡过程一致,提高整个系统的稳定性。
3.1 惯量匹配推导
针对传统同步电源,等值电源的调差系数是各台同步电源调差系数的倒数,即
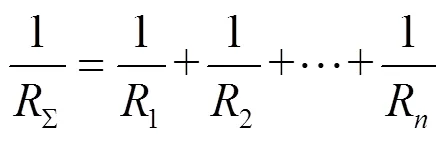
可用下垂系数式(11)表示。
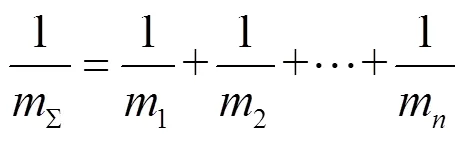
从而,由等值电源的概念,可以将“风火/光火”打捆送端电网中的两类电源等效为一类等值电源后再进行惯量匹配,会使惯量匹配方法的复杂程度大幅度降低。

式中,inv2=j-inv2/2。
假设扰动前后逆变电源工作点Q1和Q2,系统达到稳态时m1-inv2=e1-inv2,m2-inv2=e2-inv2。
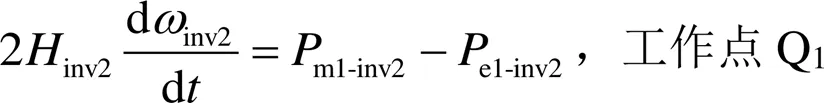
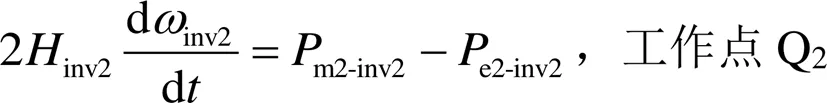
由式(5)可得

由下垂控制原理可知,当“风火/光火”打捆送端电网中Inv2出力占比改变时,其输出功率由e1-inv2变为e2-inv2,工作点由Q1变为Q2。但此时Inv2的输出指令值并没有立即响应,即
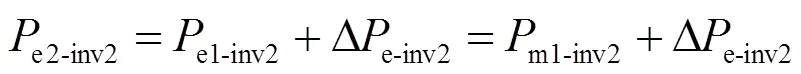
联立式(14)和式(17),可得
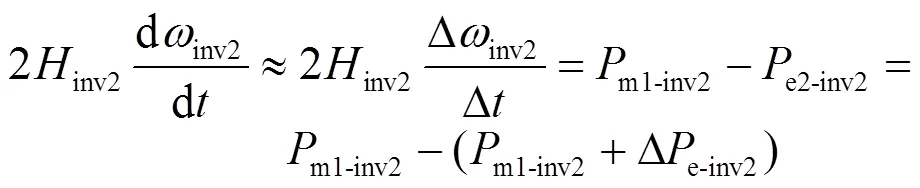
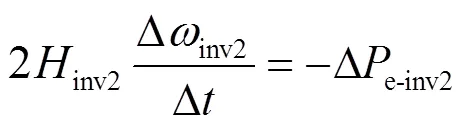
联立式(16)和式(19),可得
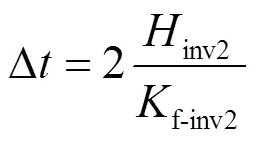
在“风火/光火”打捆送端电网中,SG1也具有上述与Inv2类似过程,当负荷扰动引起系统频率波动时,若要使SG1和Inv2获得相同的过渡时间Δ,由式(20)可知,两者的惯性时间常数必须按照各自有功调频系数的比例进行配置。
一般情况下,为了使“风火/光火”打捆送端电网中并列运行电源能够按容量比例分担负荷,SG1和Inv2的参数之间必须满足式(21)的关系。
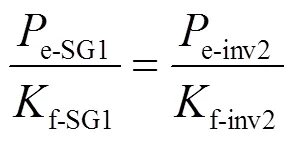
在“风火/光火”打捆送端电网中,Inv2出力占比为w,SG1出力占比为1-w,联立式(20)、式(21),得到式(22)。
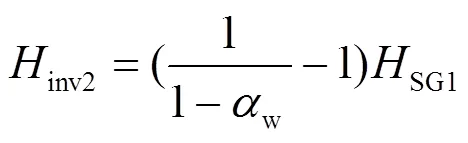
式(22)说明,要使送端电网中所有电源的过渡过程一致,Inv2的出力占比w越大,其惯量常数整定值越大。表5给出典型逆变电源出力占比情况下inv2/SG1的比值。

表5 典型αw情况下Hinv2/HSG1的比值
3.2 仿真验证
为了验证3.1节提出的惯量改进方法的有效性,在RT-LAB半实物仿真平台搭建与小信号模型一致的测试系统,测试系统参数按照表1所示设置。
区域I:有功负荷为400 MW,无功负荷为140 Mvar,采用下垂控制。区域II:有功负荷为400 MW,无功负荷为140 Mvar,采用下垂控制和惯量控制。区域III:有功负荷为600 MW,无功负荷为150 Mvar,采用下垂控制和惯量控制。
1) 工况一:w为10%
当w= 10%时,整个控制过程SG1和Inv2输出有功功率的情况如图10(a)所示,无功功率的情况如图10(b)所示。
如图10(a)所示,区域I、区域II和区域III内SG1和Inv2有功功率输出完全按照容量比分配,并且采用下垂控制和惯量控制,当增加负荷时,过渡过程输出有功功率始终保持容量比。如图10(b)所示,区域I内SG1和Inv2无功功率输出明显不是按照容量比分配;区域II和区域III内SG1和Inv2无功功率输出完全按照容量比分配。
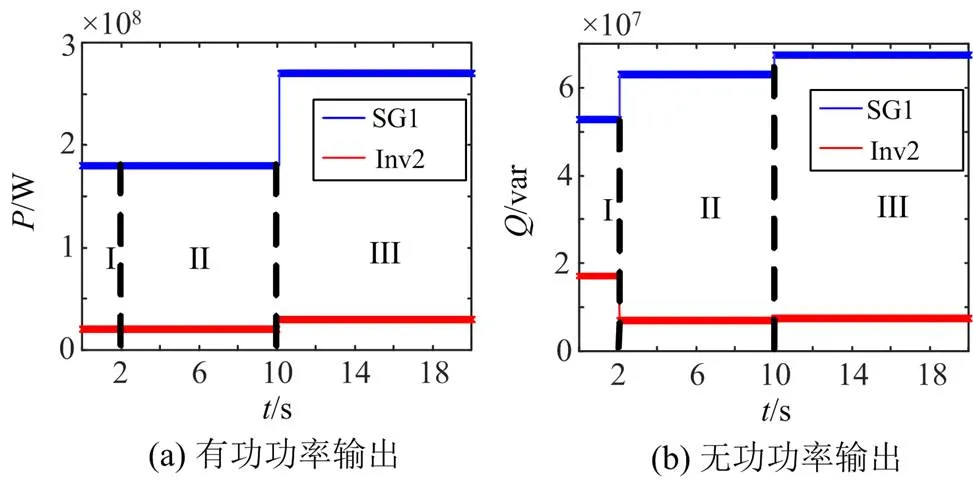
图10 αw=10%有功无功输出情况
2) 工况二:w为20%
当w= 20%时,整个控制过程SG1和Inv2输出有功功率的情况如图11(a)所示,无功功率的情况如图11(b)所示,具体数值如表6所示。

图11 αw=20%有功无功输出情况

表6 αw=20%功率输出情况
当w= 20%和w= 10%时类似,下垂控制和惯量控制均能保证有功功率按照容量比输出,但是下垂控制不能保证无功功率按照容量比输出,而惯量控制可以保证无功功率按照容量比输出。
经过RT-LAB仿真验证可知,当w取其他数值时,也可以得到相同的结论,验证了本文所提出的针对“风火/光火”打捆送端系统的惯量匹配方法的有效性。
4 结论
本文建立了“风火/光火”送端系统小信号模型,重点分析了送端电网区域内低频振荡模态,提出了SG1和Inv2的惯量匹配表达式,并完成RT-LAB仿真验证,主要结论如下。
1) 分析了惯性时间常数和有功调频系数对送端电网区域内低频振荡的影响,当Inv2出力占比w=10%时,SG1对低频振荡的影响更明显。
2) 分析了内部线路阻感比(1/1),内部线路长度1和Inv2出力占比w对送端电网区域内低频振荡的影响,当1/1越大,1越小,w越大,低频振荡模态对应的阻尼比越大,越有利于送端电网稳定。
3) 推导了送端电网SG1和Inv2的惯量表达式,w越大,inv2越大,送端电网采用惯量匹配控制时,负荷稳态和暂态过程中按SG1和Inv2容量比分配,提高了送端电网的稳定性。
[1] 陈泽雄, 张新民, 王雪锋, 等. 分布式光伏电站接入配电网的分布鲁棒优化配置方法[J]. 电力系统保护与控制, 2021, 49(13): 30-42.
CHEN Zexiong, ZHANG Xinmin, WANG Xuefeng, et al. A distributionally robust optimal allocation method for distributed photovoltaic generation stations integrated into a distribution network[J]. Power System Protection and Control, 2021, 49(13): 30-42.
[2] 丁理杰, 刘姗梅, 史华勃. 水电高占比电网中水轮机模型对频率振荡特性影响及其适应性分析[J]. 电力系统保护与控制, 2021, 49(12): 174-180.
DING Lijie, LIU Shanmei, SHI Huabo. Influence of a turbine model on frequency oscillation characteristics and its adaptability in a high hydro-ratio power grid[J]. Power System Protection and Control, 2021, 49(12): 174-180.
[3] 孙亮, 杨晓飞, 孙立国, 等. 基于改进虚拟同步发电机的多逆变器频率无差控制策略[J]. 电力系统保护与控制, 2021, 49(11): 18-27.
SUN Liang, YANG Xiaofei, SUN Liguo, et al. Frequentdeviation-free control for microgrid multi-inverters based on improving a virtual synchronous generator[J]. Power System Protection and Control, 2021, 49(11): 18-27.
[4] ZHAO Yingying, AN Aimin, XU Yifan, et al. Model predictive control of grid-connected PV power generation system considering optimal MPPT control of PV modules[J]. Protection and Control of Modern Power Systems, 2021, 6(4): 407-418.
[5] ALIPOOR J, MIURA Y, ISE T. Stability assessment and optimization method for microgrid with multiple VSG units[J]. IEEE Transactions on Smart Grid, 2018, 9(2): 1462-1471.
[6] 钟庆昌. 虚拟同步机与自主电力系统[J]. 中国电机工程学报, 2017, 37(2): 336-348.
ZHONG Qingchang. Virtual synchronous machines and autonomous power systems[J]. Proceedings of the CSEE, 2017, 37(2): 336-348.
[7] 蒋雯倩, 谭骞, 吕志鹏, 等. 三相四桥臂并网逆变器模拟同步发电机控制策略[J]. 智能电网, 2015, 3(8): 683-689.
JIANG Wenqian, TAN Qian, LÜ Zhipeng, et al. Research of three-phase four-wire grid-connected inverter which mimics synchronous generator characteristic[J]. Smart Grid, 2015, 3(8): 683-689.
[8] ACKERMANN T. Wind power in power systems[M]. Chichester: John Wiley and Sons Ltd., 2005.
[9] 薛禹胜, 雷兴, 薛峰, 等. 关于风电不确定性对电力系统影响的评述[J]. 中国电机工程学报, 2014, 34(29): 5029-5040.
XUE Yusheng, LEI Xing, XUE Feng, et al. A review on impacts of wind power uncertainties on power systems[J]. Proceedings of the CSEE, 2014, 34(29): 5029-5040.
[10] WANG Yi, XU Lie. Coordinated control of DFIG and FSIG-Based wind farms under unbalanced grid conditions[J]. IEEE Transactions on Power Delivery, 2010, 25(1): 367-377.
[11] DU W J, FU Q, WANG H F. Power system small-signal angular stability affected by virtual synchronous generators[J]. IEEE Transactions on Power Systems, 2019, 34(4): 3209-3219.
[12] 张波, 颜湘武, 黄毅斌, 等. 虚拟同步机多机并联稳定控制及其惯量匹配方法[J]. 电工技术学报, 2017, 32(10): 42-52.
ZHANG Bo, YAN Xiangwu, HUANG Yibin, et a1. Stability control and inertia matching method of multi-parallel virtual synchronous generators[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 42-52.
[13] 中国国家标准化管理委员会. 风电场接入电力系统技术规定: GB/Z 19963—2011[S]. 北京: 中国标准出版社, 2012.
Standardization Administration of the People's Republic of China. Technical rule for connecting wind farm to power network: GB/Z 19963—2011[S]. Beijing: Chinese Standard Press, 2012.
[14] 中国国家标准化管理委员会. 光伏发电站接入电力系统技术规定: GB/Z 19964—2012[S]. 北京: 中国标准出版社, 2013.
Standardization Administration of the People’s Republic of China. Technical rule for connecting solar generation to power network: GB/Z 19963—2012[S]. Beijing: Chinese Standard Press, 2013.
[15] ZHONG Q, WEISS G. Synchroverters: inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1267.
[16] 孙大卫, 刘辉, 李蕴红, 等. 风火/光火打捆系统中逆变电源调频与惯量控制对低频振荡的影响机理[J]. 中国电机工程学报, 2021, 41(17): 5947-5957.
SUN Dawei, LIU Hui, LI Yunhong, et al. Effect mechanism of primary frequency and virtual inertia control of inverter power on low frequency oscillation in wind-thermal/solar-thermal bundled system[J]. Proceedings of the CSEE, 2021, 41(17): 5947-5957.
[17] KAWABE K, TANAKA K. Impact of dynamic behavior of photovoltaic power generation systems on short-term voltage stability[J]. IEEE Transactions on Power Systems, 2015, 30(6): 3416-3424.
[18] 高娟, 秦岭. 虚拟同步发电机的输入阻抗建模及稳定性分析[J]. 电网技术, 2021, 45(24): 578-588.
GAO Juan, QIN Ling. Input impedance modeling and stability analysis for virtual synchronous generator[J]. Power System Technology, 2021, 45(24): 578-588.
[19] POGAKU N, PRPDANOVIC M, GREEEN T C. Modeling, analysis and testing of autonomous operation of an inverter-based microgrid[J]. IEEE Transactions on Power Electronics, 2007, 22(2): 613-624.
[20] 孙大卫, 刘辉, 赵峰, 等. 不同逆变电源主动支撑控制方式的对比研究[J]. 电网技术, 2019, 40(3): 910-917.
SUN Dawei, LIU Hui, ZHAO Feng, et al. Comparison of inverter generators with different support control methods[J]. Power System Technology, 2019, 40(3): 910-917.
[21] DU W J, FU Q, WANG H F. Concept of modal repulsion for examining the subsynchronous oscillations caused by wind farms in power systems[J]. IEEE Transactions on Power Systems, 2019, 34(1): 518-526.
[22] LIU J, MIURA Y, BEVRANI H, et al. Enhanced virtual synchronous generator control for parallel inverters in microgrids[J]. IEEE Transactions on Smart Grid, 2017, 8(5): 2268-2277.
[23] 贺静波, 庄伟, 许涛, 等. 暂态过电压引起风电机组连锁脱网风险分析及对策[J]. 电网技术, 2016, 40(6): 1839-1844.
HE Jingbo, ZHUANG Wei, XU Tao, et al. Study on cascading tripping risk of wind turbines caused by transient overvoltage and its countermeasures[J]. Power System Technology, 2016, 40(6): 1839-1844.
Effect of an inverter on low frequency oscillation of wind-thermal/solar-thermal bundled sending-end power grid and inertia matching method
WANG Qian, SHENG Siqing, TIAN Haojing
(School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071003, China)
In order to study the influence of the inverter (Inv) on the stable operation of the "wind-thermal/solar-thermal" bundled sending-end power grid, a control model that takes into account the system parameters and the inertia matching method of different types of power sources are proposed. First, this paper constructs the mathematical model of all the control links of Inv, and then forms the small signal model of the entire research system, which is verified by Matlab simulation. Secondly, based on the small-signal model, the root locus method is used to analyze the influence of system parameters on the internal low-frequency oscillation of the sending-end power grid. The study shows that the shorter the internal line of the sending-end power grid, the larger the resistance-inductance ratio and the more the Inv output, which is more conducive to system stability. Finally, using the principle of equivalent power supply, the inertia matching method of the two types of power sources in the sending-end power grid is derived. The RT-LAB semi-physical simulation verifies that the proposed inertia matching formula can better distribute power and improve the stability of the sending-end power grid.
inverter; sending-end power grid; small signal model; low-frequency oscillation; inertia matching
10.19783/j.cnki.pspc.210934
国家电网公司科技项目资助“高比例电力电子型电源接入对电力系统稳定性影响机理及控制措施研究”(5100-201955014A-0-0-00)
This work is supported by the Science and Technology Project of State Grid Corporation of China (No. 5100-201955014A-0-0-00).
2021-07-20;
2021-12-14
王 倩(1995—),女,通信作者,硕士研究生,主要研究方向为新能源并网及其稳定性。E-mail: 946262936@ qq.com
(编辑 许 威)

