基于长短期记忆网络的UKF动态谐波状态估计

黄蔓云，王天昊，卫志农，孙国强

基于长短期记忆网络的UKF动态谐波状态估计

黄蔓云，王天昊，卫志农，孙国强

(河海大学能源与电气学院，江苏 南京 211100)

传统动态谐波状态估计的卡尔曼滤波预测步通常以单位阵构建状态空间模型，同时将系统噪声协方差矩阵假设为常数阵，从而导致动态估计预测精度降低，影响动态状态估计模型的滤波性能。为了准确建立谐波状态的空间模型，提出一种基于长短期记忆网络(Long Short-Term Memory, LSTM)的时序预测方法。通过大量历史数据离线训练模拟复杂的状态转移过程，基于历史时刻的滤波估计值预测当前时刻的谐波状态量，有效提高无迹卡尔曼滤波(Unscented Kalman Filter, UKF)中预测模型精度。在改进IEEE34节点三相不平衡系统上进行了测试分析。与传统算法进行对比，结果证明所提出的方法在谐波状态估计精度和鲁棒性方面均表现更好。

动态谐波状态估计；无迹卡尔曼滤波；长短期记忆网络；预测模型；鲁棒性

0 引言

近年来，高渗透率的分布式能源与广泛使用的电力电子元件使得电网中的谐波污染问题变得愈发严重[1]。为了治理谐波污染，保障电力设备安全，需要对电网谐波进行实时监测[2-5]，谐波状态的准确估计是谐波实时监测的基础功能和模块[6-8]。谐波状态估计能够利用有限的谐波测量装置提供的数据推断出全网节点和支路谐波状态[9-12]，节约了谐波测量装置的配置成本，对电力系统谐波治理具有重要意义。

传统的动态谐波状态估计以卡尔曼滤波算法为核心，以单位阵为状态空间模型，这使得其预测步的作用大大降低，估计精度受到限制。文献[13]基于电压幅值和线路功率量测，利用卡尔曼滤波算法估计谐波状态，但其状态转移矩阵仍然为单位阵。文献[14]将谐波源进行小波分解并分别计算系统噪声协方差矩阵和状态转移矩阵，建立了状态空间模型。面对大电网的高维非线性问题，UKF算法逐渐得到广泛应用。文献[15]提出了一种广义无迹卡尔曼滤波算法，利用统计线性化方法进行了准确估计，并能够有效辨识量测坏数据。文献[16]提出了一种基于混合量测的无迹卡尔曼滤波算法，避免了线性化误差的引入和雅可比矩阵的计算，提高了动态状态估计的性能。文献[17]提出了一种自适应UKF估计方法，能在未知系统噪声下进行准确估计。以上谐波动态状态估计的研究中，UKF算法的状态转移矩阵通常都设为单位阵，或通过Holt's两参数指数平滑法构建状态空间模型。这些方法假设系统噪声协方差矩阵保持恒定，仿真结果具有较高的精度。然而这种状态空间模型的构建方式并没有基于实际的谐波模型，仅通过数学方程近似卡尔曼滤波的状态转移过程，使得动态状态估计预测步精度受到限制，最终影响滤波步估计结果[18]。

针对传统动态谐波状态估计预测步状态空间模型难以建立的特点，本文提出基于LSTM神经网络的状态空间模型，通过历史数据的特征提取模拟复杂的状态转移关系，然后采用UKF算法进行动态谐波状态估计。本文所提方法首次通过数据驱动的方式建立谐波电压状态空间模型，并将系统噪声协方差矩阵考虑在内，避免了传统卡尔曼滤波方法中由常系数的状态转移矩阵引起的状态空间模型误差，有效提高了UKF预测步的精度，进而提高了谐波状态的滤波精度。仿真结果表明，本文所提方法相较于传统谐波动态状态估计方法的预测和滤波精度更高，鲁棒性能更优。

1 UKF动态谐波状态估计数学模型

1.1 无迹变换基本原理

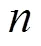
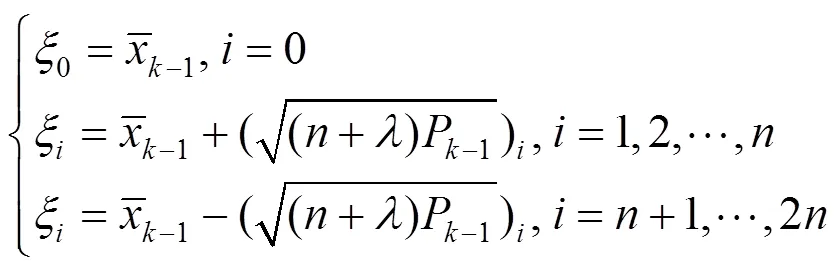
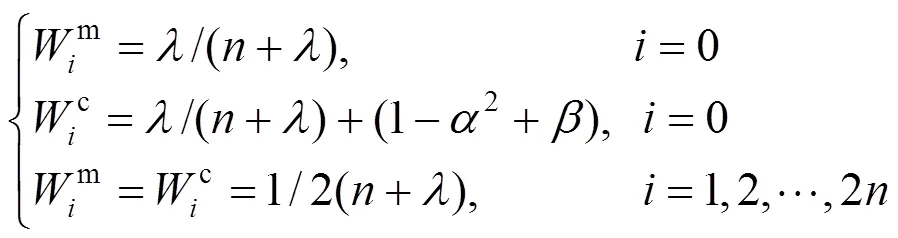
1.2 基于UKF的谐波状态估计模型

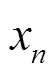
2) 状态预测步

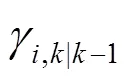
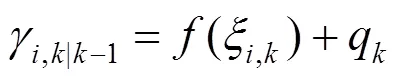
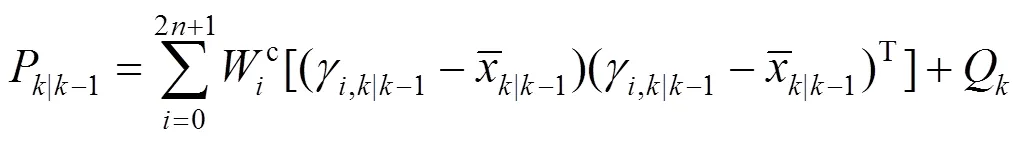
3) 量测预测步

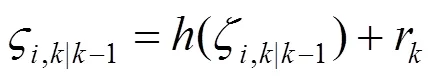
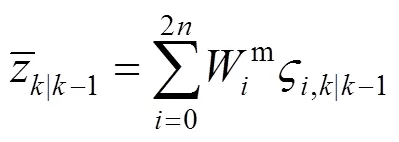
4) 滤波步

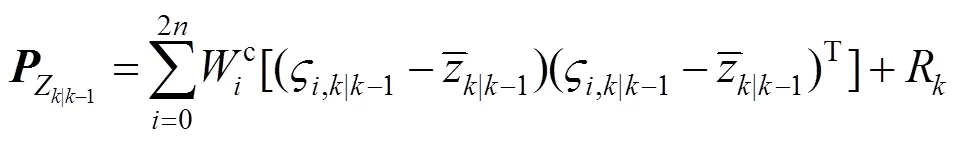
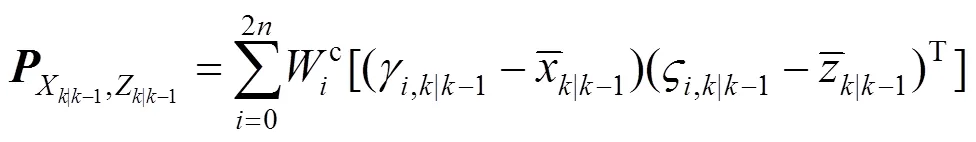
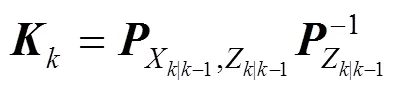
2 基于LSTM的时序预测模型

本文所构建的LSTM模型以节点谐波电压和误差协方差矩阵作为网络的输入输出特征量，各次谐波均彼此独立且具备时序特征。LSTM作为一种时间递归神经网络[22]，其基本单元如图1所示。

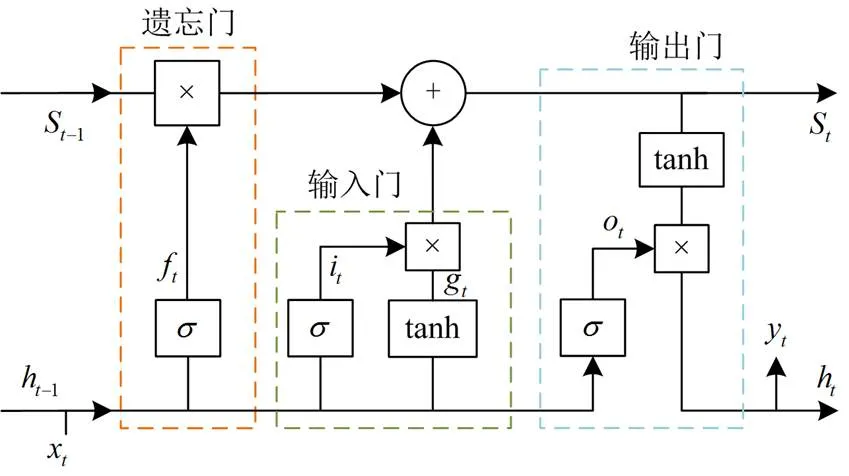
图1 LSTM基本单元

LSTM网络包含输入门、遗忘门和输出门三个部分。本文算法的网络输入即为节点电压和误差协方差矩阵，通过遗忘门决定上一时刻保留到当前时刻的单元状态数量，输出门则控制当前时刻的输入保存到当前单元状态的数量，最终输出由输出门和单元状态共同决定，从而达到了长期记忆对当前输出影响的目的，输出量即为下一时刻电压和误差协方差矩阵的预测值。

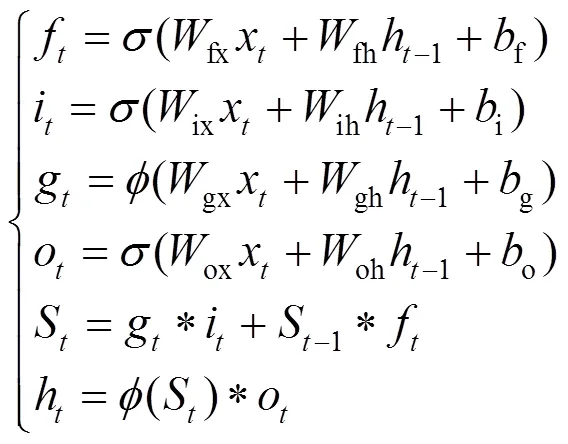
3 LSTM-UKF动态谐波状态估计方法

3.1 LSTM模型搭建

图2 LSTM网络模型层次结构图

根据LSTM模型特征维数与本文方法数据量大小，构建如图2所示LSTM模型，其参数调优过程见附录。LSTM层的神经元数量分别为60、120、60，并根据调优过程及经验公式将每层的dropout函数均设置为20%，可以加快模型的训练速度并且有效防止网络的过拟合。训练的最大轮数为50，每次训练迭代的最小批次大小为128。

将电压与协方差矩阵分为两个LSTM模型进行训练。首先构建训练集数据库，然后将历史电压值及协方差矩阵输入，采用LSTM单步预测的方式构建状态预测模型。网络输入输出维度与状态变量维度一致。根据训练模型在未来时刻UKF计算中对上一时刻的估计值进行预测作为当前时刻的先验估计。

3.2 LSTM-UKF算法

LSTM-UKF动态谐波状态估计根据各个时间断面下部分节点谐波电压、节点谐波电流和支路谐波电流量测数据估计所有节点的谐波电压情况。通过LSTM时序模型训练真实负荷波动下的谐波电压数据和误差协方差矩阵数据，在UKF实际计算中用LSTM模型预测下一时刻的谐波电压值和误差协方差矩阵，通过数据驱动的方式替代了UKF的预测步，避免了谐波复杂模型的建立。将预测后的电压值通过比例采样算法变换得到采样点，然后进行量测预测步和滤波步的计算，当前时刻所有节点估计结束时，进行下一时刻的状态估计；若所有时刻均估计结束，则输出数据，程序终止。

本文算法流程图如图3所示。

图3 算法流程图

通过上一时刻的滤波步结果实时更新LSTM网络模型，提高了LSTM训练模型随负荷波动的自适应能力，且仅需对历史数据进行一次离线训练，满足实际电网运行的实时性要求。

4 算例分析

在改进三相不平衡系统IEEE34节点算例上对本文方法进行测试，其网络拓扑结果以及实时量测配置情况如图4所示，配有电能质量监测装置的节点能够获取节点谐波电压、节点谐波电流以及相邻支路谐波电流量测数据[23]。在尽可能减小谐波量测装置配置成本的情况下，该量测配置方案能够满足系统可观性要求[24]，同时具备较高的估计准确性。通过对谐波源进行建模，采用三相全桥逆变器作为谐波注入设备，谐波源节点的各次谐波电流幅值及相位根据基波电流向量进行调整。将谐波源节点设置于26、33处，各谐波源地理和电气距离较远，符合电网的实际情况。

某地区某月真实负荷曲线采样间隔为15 min，选择连续采样所得的3 100组数据对标准算例的PQ负荷波动处理，模拟电网实际运行中的动态过程，该曲线依据实际某省网归一化得出，其负荷波动曲线详见附录。若掌握真实的年负荷曲线进行训练，可以通过典型日选取[25]等手段，挑选具有代表性的负荷曲线集进行训练，使得训练后的模型适应性强，同时训练效率高。根据负荷曲线计算多时间断面的基波潮流计算的结果，并根据基波潮流结果计算谐波源注入电流，谐波频谱如表1所示。通过谐波导纳矩阵计算得全网的谐波电压、支路谐波电流[26]，并将其作为测量值，通过添加均值为0，标准差为0.01的高斯白噪声获得含噪量测数据。经计算得全网的谐波电压估计值后，与谐波导纳矩阵进行计算即可得谐波电流估计结果。

我不敢再叫了，吓得直往后退缩，一直退到墙角，蹲在那儿发抖。鼻子里像两条毛毛虫在爬，我伸手一摸，满手的血。鼻血不断线地往出涌，地上很快洇红了一大片。我仰起头，鼻血倒流，和着泪水往嗓子眼儿灌，漾起令人作呕的铁腥气。

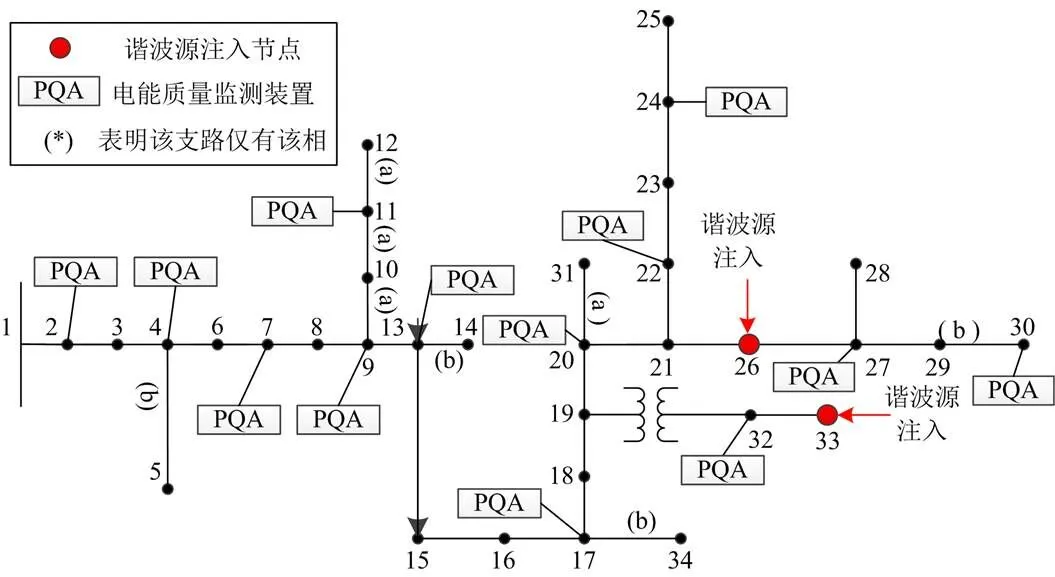
图4 算例拓扑与量测配置

表1 谐波源频谱表

为了获得LSTM模型电压以及误差协方差矩阵训练集数据，本文首先计算历史时刻3 000组断面的谐波电压和误差协方差矩阵数据，并将其输入LSTM模型进行训练。在未来时刻的100组断面上对电压以及误差协方差矩阵数据进行预测，由预测得到的电压和误差协方差矩阵变换得到Sigma点，然后进行UKF滤波步的计算，最终比较预测步和滤波步的估计精度。

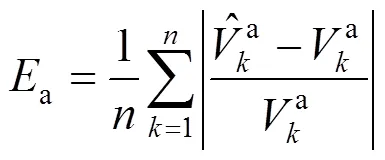
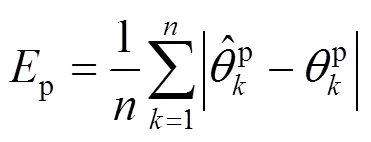
4.1 LSTM离线训练

根据3 000组断面的电压估计值以及误差协方差矩阵数据，选择前2 400组作为LSTM模型的训练集，后600组数据为测试集。

以26节点A、B两相的5次谐波电压训练数据为例，得到电压幅值的训练集拟合结果如图5所示，这表明训练集有较高的预测精度。

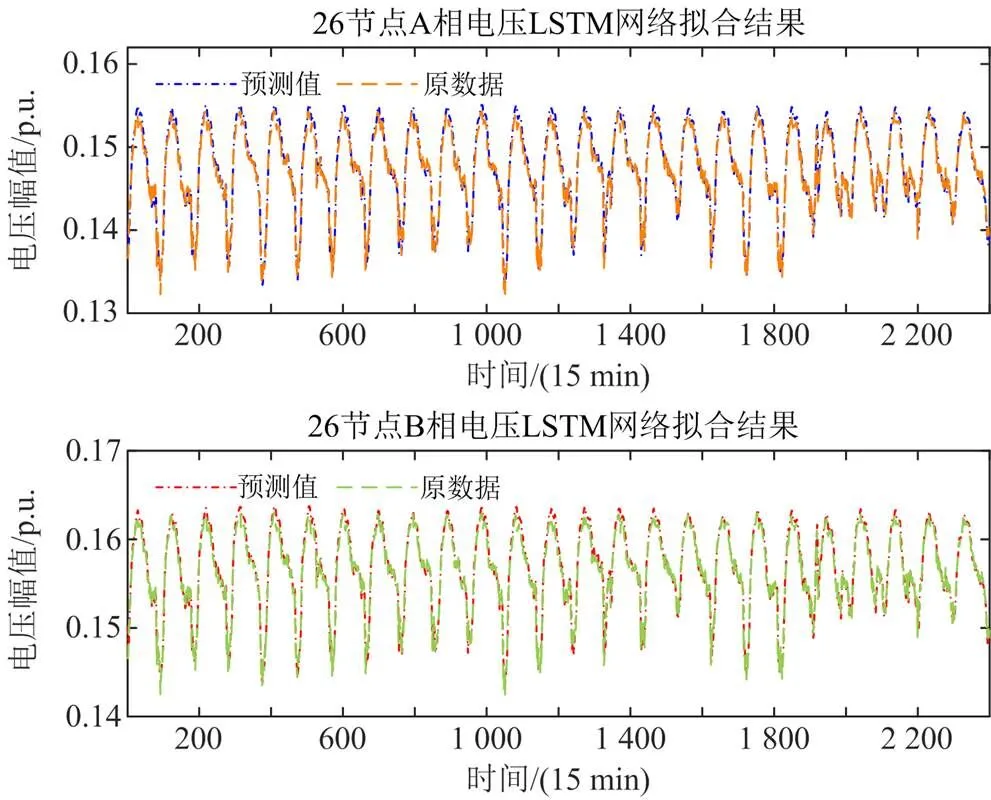
图5 训练集电压拟合结果

LSTM模型训练过程中训练集的预测值与测试集的预测值如图6所示。前2 400组为训练集结果，后600组为测试集结果，这表明对未训练的数据也有较高的预测精度。

可以看出，电压训练集预测值能够较好跟踪原数据，且测试集数据同样具备与训练集相似的时序特征，这说明所搭建的LSTM训练模型结构合理，具有较高的预测精度，能够替代UKF的预测步。为了与预测后的电压值相对应，对UKF计算过程中误差协方差矩阵进行同步预测。由于预测电压与误差协方差矩阵彼此独立，且各次谐波之间的预测模型也彼此独立，所以在离线计算时可以单机同步运行，训练时间仅为训练模型的最长时间，在本文LSTM神经网络的数据结构设置下，最大训练时间为44 s，且相关神经网络只需进行一次训练，后续时刻的滤波步结果可以实时更新网络，可以避免数据重复占用内存。

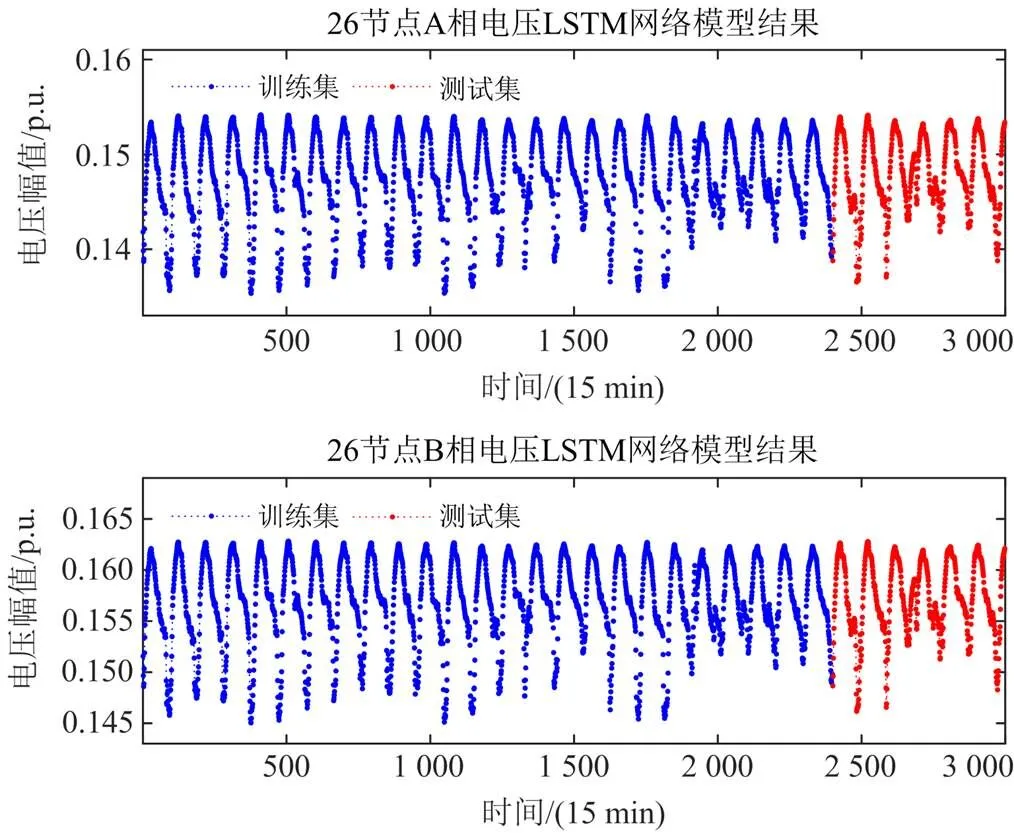
图6 电压训练集预测值及测试集预测值

4.2 LSTM-UKF估计精度分析

1) 本文方法估计结果分析

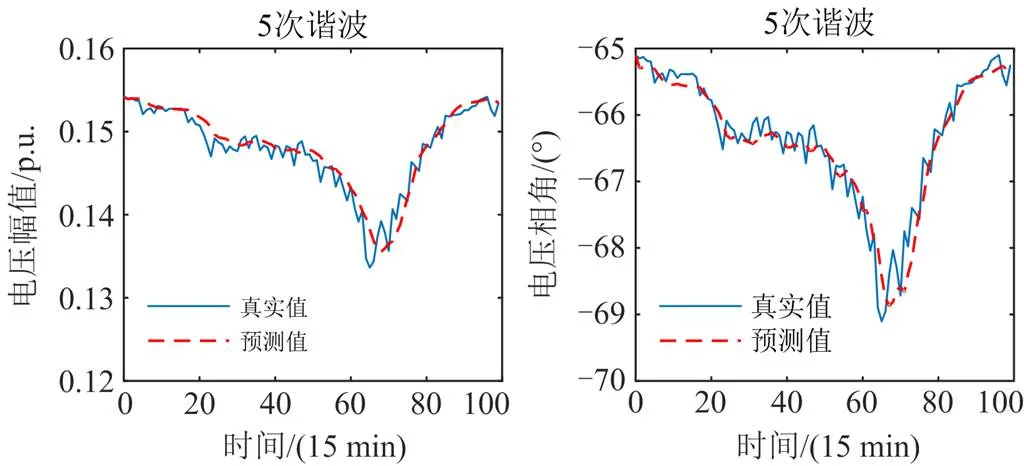
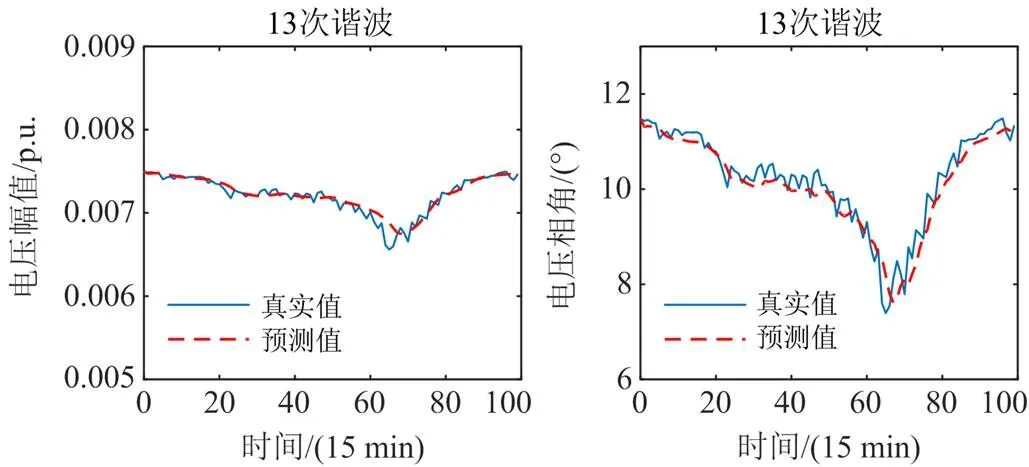
图7 26节点A相各次谐波预测步精度

对比预测步曲线与真实值曲线，预测步的结果能够较好地跟踪真实值曲线，这表明所构建的LSTM预测模型对谐波电压状态量预测精度较高。表2列出各谐波源注入节点的预测步误差。

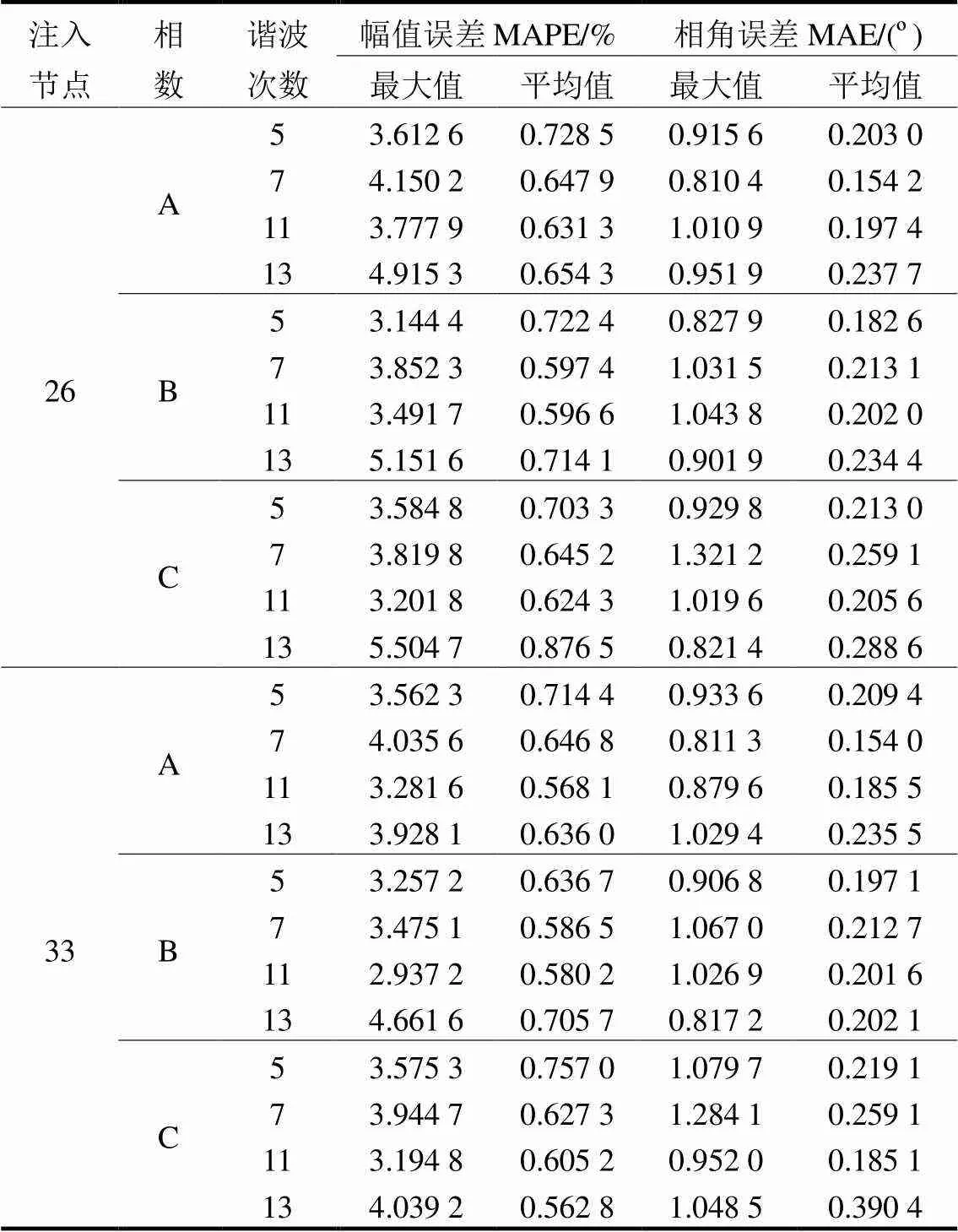
表2 谐波源注入节点电压状态量预测步误差

在实时量测数据到来后，通过滤波步计算校正预测步的估计值，从而得到最优估计值。将谐波电压幅值与电压相角的滤波步估计结果与真实值进行比较，根据图8对各次谐波滤波步估计结果与真实值的比较，可以明显看出滤波步结果能够较好地跟踪真实值，各次谐波电压幅值与相角均具有准确的估计结果。

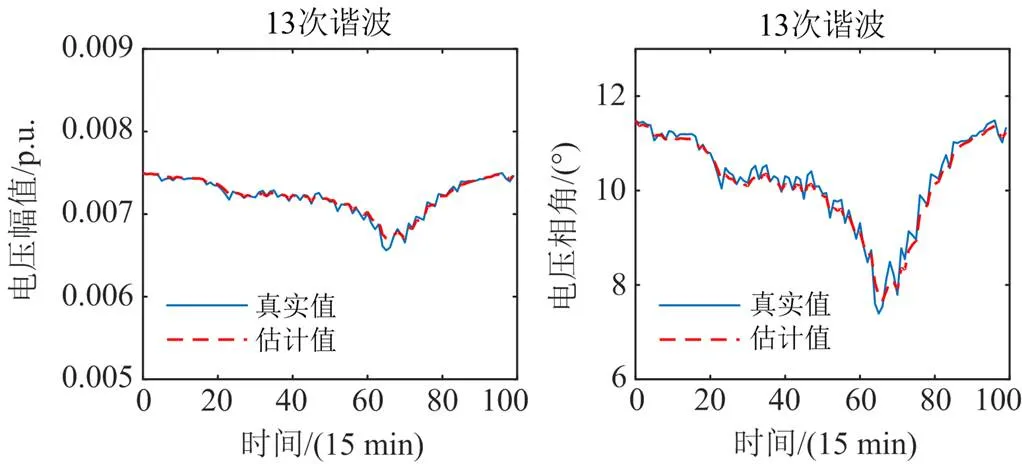
图8 26节点A相各次谐波滤波步估计精度

为了进一步比较滤波步估计结果的精度，表3列出各谐波源注入节点的滤波步估计误差。

本文测试的硬件平台基于PC机，处理器为Intel® Core™ i5-6300HQ CPU @ 2.30GHz，内存为12.0 GB。

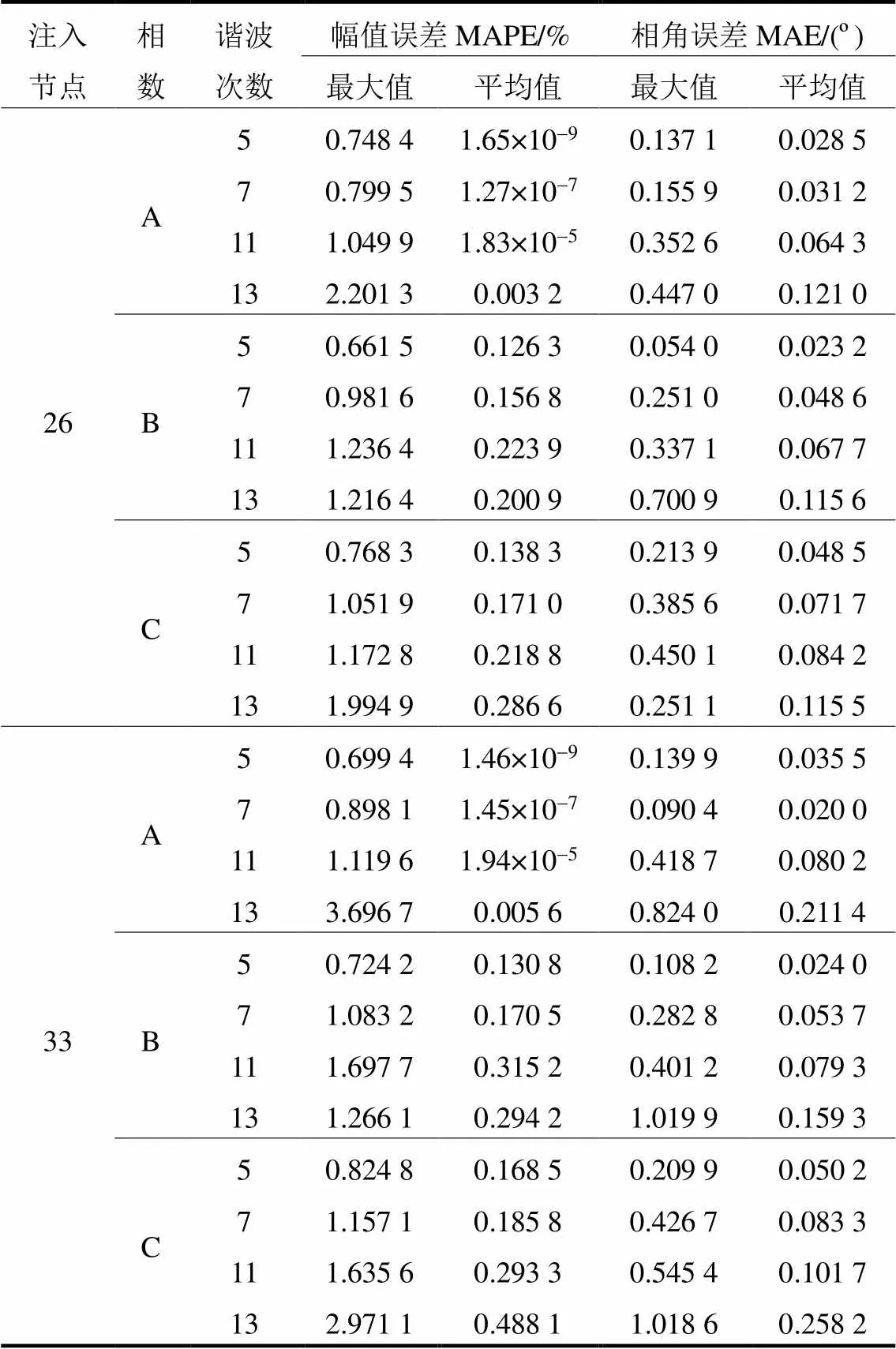
表3 谐波源注入节点电压状态量滤波步误差

经过仿真结果分析，本文方法利用LSTM训练模型进行100个断面各次谐波的估计共耗时102 s。由于各次谐波的LSTM神经网络模型彼此独立，各次谐波的量测量也彼此独立，所以在本文方法中，针对各次谐波可以独立进行动态状态估计，因此单断面下单次谐波估计耗时仅为0.255 s。以电网实际运行10 min采样一次为例，本文方法的计算效率能够满足实际电网的运行要求，可以对电网谐波状态精确实时估计。

2) 与传统方法估计精度对比

由于谐波数学模型难以精确建立，目前在UKF动态谐波状态估计的研究中主要以单位阵、Holt's数学模型作为状态空间模型为主，这种状态模型的构建方式常常使得UKF的预测步估计精度较低，从而估计精确度主要依赖于滤波步的计算，而本文通过LSTM的预测方法，进一步提高了传统UKF算法的预测步估计精度，同时增强了UKF的估计鲁棒性。

由相同真实负荷曲线模拟量测数据的情况下，将本文方法与状态转移矩阵为单位阵、Holt's模型为状态空间模型的方法进行比较。以改进三相不平衡系统IEEE34节点算例为例，存在谐波源注入的26节点A相各次谐波电压预测步相对误差与滤波步相对误差结果如图9所示。

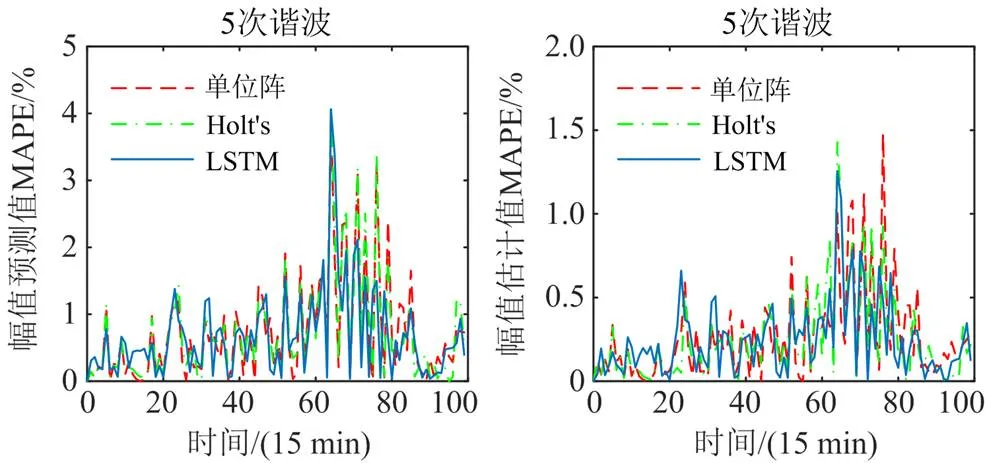
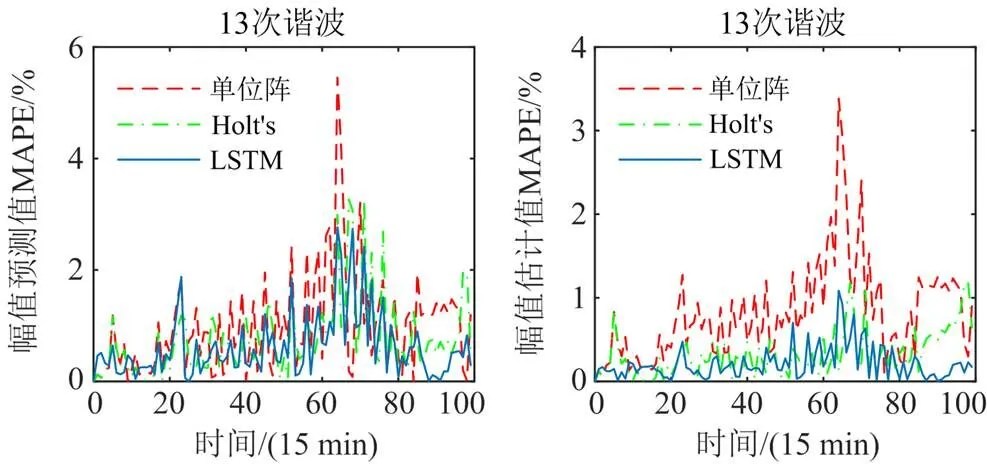
图9 三种方法预测步与滤波步误差比较

由图9可见，利用单位阵作为状态转移矩阵、Holt's模型作为状态空间模型的方法由于系统噪声的存在，其预测步精度低于LSTM时序预测的方法，因此在三种状态空间模型的UKF计算方法下，LSTM模型预测步电压状态量估计值的精度更高，且计算实时性能够满足电网的实际运行要求。

4.3 LSTM-UKF鲁棒性分析

为验证本文所提方法在实际电网运行中的鲁棒性，本文对改进IEEE34节点的5次谐波进行分析，随机分布坏数据量测位置，比例约占总量测的10%左右，符合电网实际运行情况。

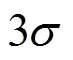
如图10所示为含坏数据情况下26节点A相5次谐波电压预测步与滤波步误差计算结果，其余次数谐波的鲁棒性分析详见附录。表4、表5为具体估计误差结果分析，显然当存在坏数据时，本文所提方法的鲁棒性更好。

图10 不良数据时状态预测和估计误差

表4 含坏数据下三种方法预测步估计误差对比

表5 含坏数据下三种方法滤波步估计误差对比

2) 为了进一步验证所提方法针对坏数据时仍具有较高的鲁棒性，将正常量测增大或缩小50%～ 200%来模拟量测坏数据，如图11为鲁棒性测试结果。

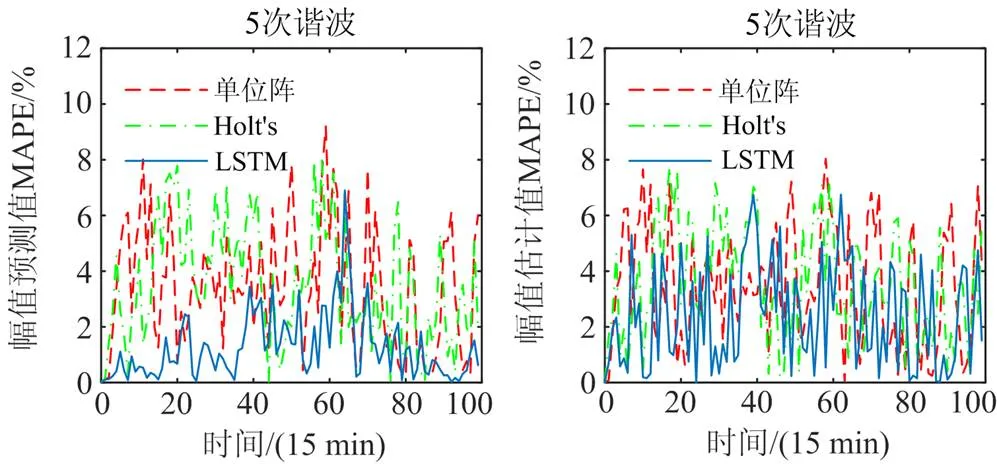
图11 坏数据时状态预测和估计误差

在电网实际运行中存在量测坏数据的情况下，本文方法在训练时将历史时刻的估计值考虑在内，所以其预测步仍具有较高的精度。当进行滤波步计算时，传统方法仅根据前一时刻的估计值进行预测，所以预测步精度较低。而UKF的估计精度取决于预测步和滤波步，本文方法相比传统方法预测步的精度大大提高，故具有较高的鲁棒性。

5 结论

为进一步发挥动态谐波状态估计的预测优势，解决传统UKF算法中的预测步状态空间模型难以建立的问题。本文提出一种基于LSTM神经网络的状态空间模型，基于历史状态量数据特征提取，通过数据驱动的方法模拟复杂的状态转移关系。利用LSTM长短时记忆神经网络的优势，建立了准确的状态空间模型，提高了UKF的预测性能。仿真结果表明，该方法相比于传统的UKF计算方法无论是预测步还是滤波步精度均明显提高，且LSTM-UKF算法在噪声均值非零、方差增大的情况下仍具备较好的估计精度和鲁棒性。所提方法能够在当前时刻量测量到来之前对电网的谐波状态进行准确预测，提高了谐波状态估计的精度，有利于大电网谐波的有效监测与治理。

附录

根据LSTM模型特征维数与本文方法数据量大小，由网络层数调优分析结果选择LSTM层数为3层，为了防止网络过拟合，依据网络参数优选和经验公式设置每层的dropout函数为20%，初始学习率为0.005，如附图1所示，实际损失函数曲线表明所设置的参数能够适应所建网络的需求。其余参数的调优过程如下：

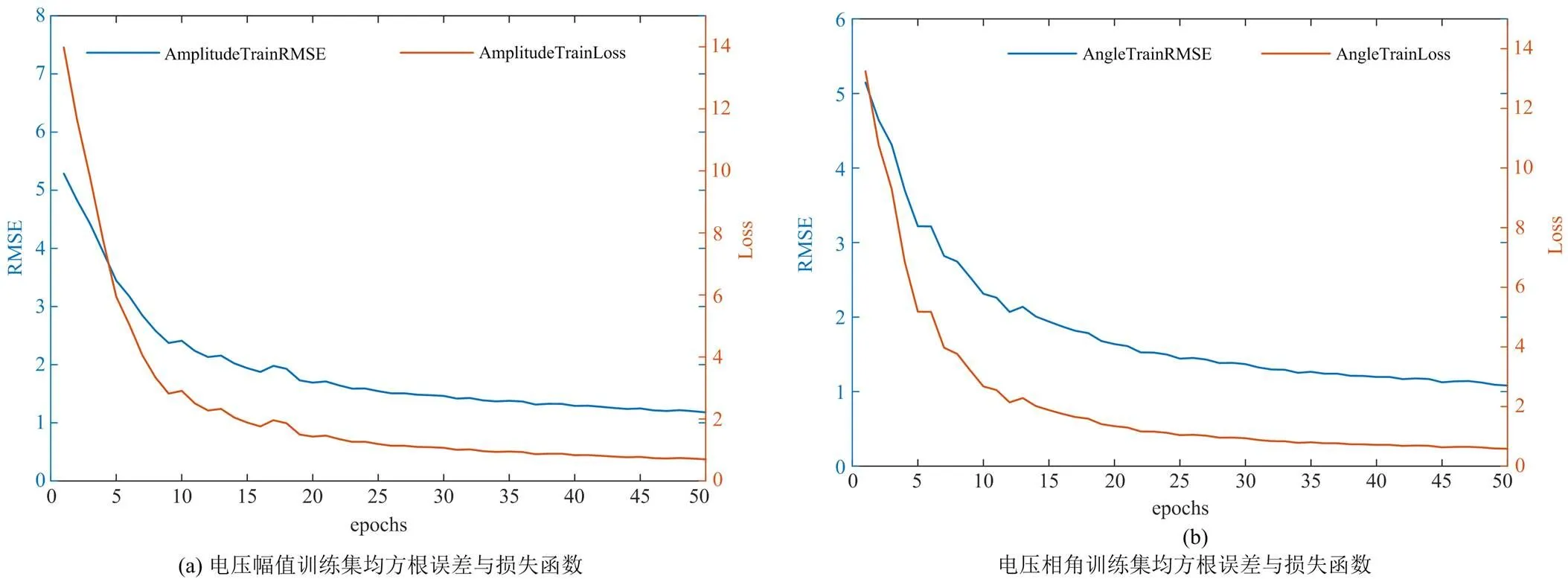
附图1 节点电压幅值与相角训练收敛曲线

Attached Fig. 1 Convergence curve of bus voltage amplitude and phase angle training

1) 确定LSTM层中神经元个数

针对所构建的LSTM模型进行网络参数调优，以谐波源注入26节点A相5次谐波电压估计结果为例，由附表1可以看出，综合测试集估计精度与训练效率，选择LSTM层中神经元个数分别为60、120、60个。

2) 确定Batch_size和Epochs

由附表2可以看出，综合测试集估计精度及训练效率，选择LSTM网络最大迭代次数Epochs为50，一次训练所选取的样本数Batch_size为128。

附表1 神经元个数调优表

Attached Table 1 Result of neuron number tuning

附表2 batch_size和epochs调优表

Attached Table 2 Result of batch_size and epochs tuning

附图2为连续4天负荷的变化情况。00：00—24：00每隔15 min采样一次，共计96个采样点。可以看出，4天的日负荷变化存在一定的波动和区别，总体上具有一定的周期性。

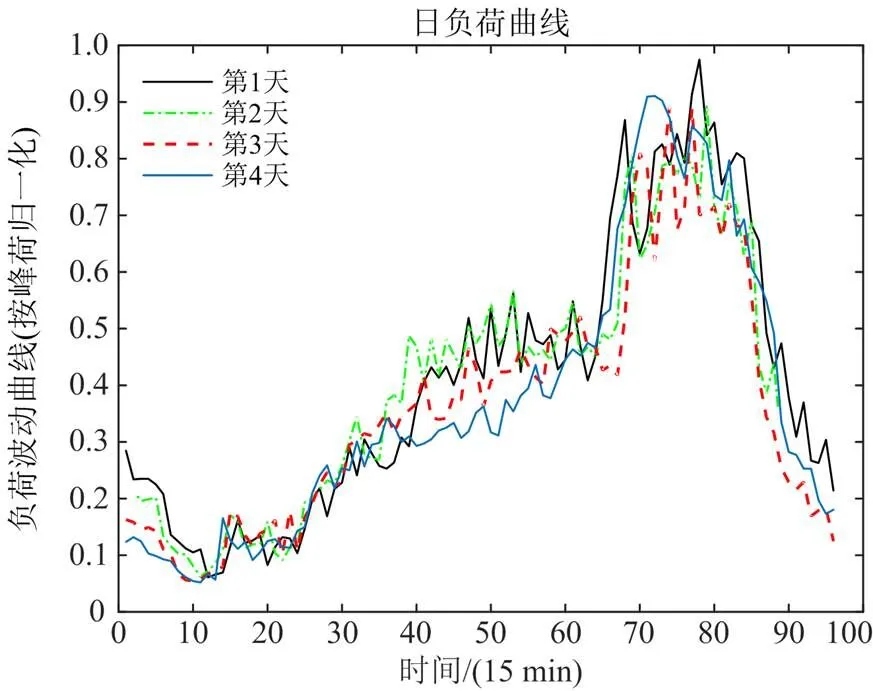
附图2 连续4天负荷变化趋势

Attached Fig. 2 Change trend of load with 4 running days

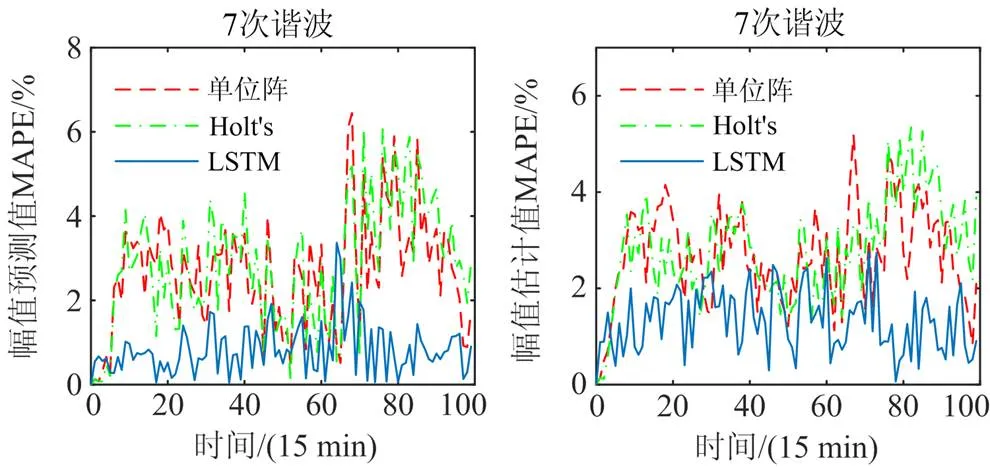
附图3 不良数据下26节点A相7次谐波电压误差比较

Attached Fig. 3 Comparison of 7th harmonic voltage errors of 26-node A phase with bad data

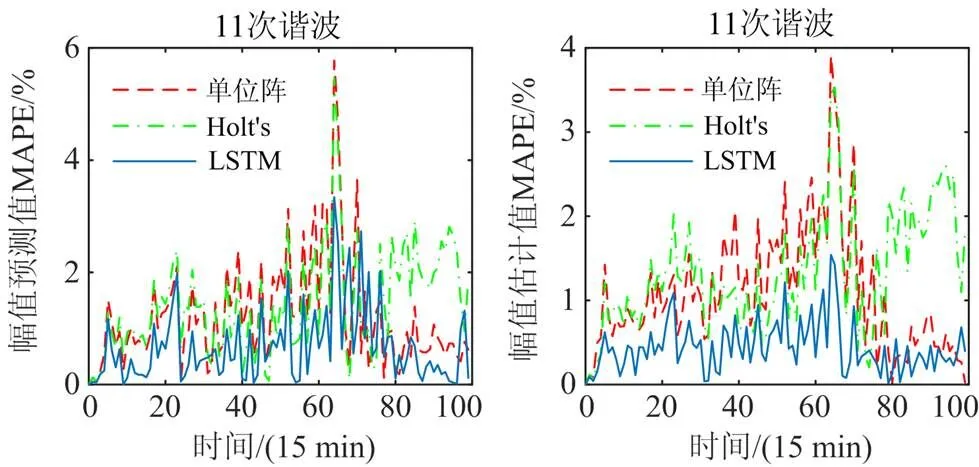
附图4 不良数据下26节点A相11次谐波电压误差比较

Attached Fig. 4 Comparison of 11th harmonic voltage errors of 26-node A phase with bad data

[1] 聂晓华. 一种基于卡尔曼滤波的电能质量扰动检测新方法[J]. 中国电机工程学报, 2017, 37(22): 6649-6658.

NIE Xiaohua. A new method of power quality disturbance detection based on Kalman filter[J]. Proceedings of the CSEE, 2017, 37(22): 6649-6658.

[2] 阳登辉, 朱明星, 徐斌. 孤网失稳状态下频率和暂态谐波分析方法[J]. 中国电力, 2021, 54(8): 27-34.

YANG Denghui, ZHU Mingxing, XU Bin. An analysis method for frequency and transient harmonics of isolated network under instable condition[J]. Electric Power, 2021, 54(8): 27-34.

[3] 李欣悦, 李凤婷, 尹纯亚, 等. 直流双极闭锁故障下送端系统暂态过电压计算方法[J]. 电力系统保护与控制, 2021, 49(1): 1-8.

LI Xinyue, LI Fengting, YIN Chunya, et al. Transient overvoltage calculation method of HVDC sending-end system under DC bipolar blocking[J]. Power System Protection and Control, 2021, 49(1): 1-8.

[4] 陈磊, 何慧雯, 王磊, 等. 基于限流器与断路器协调的混合直流输电系统故障隔离方法[J]. 电力系统保护与控制, 2020, 48(19): 119-127.

CHEN Lei, HE Huiwen, WANG Lei, et al. Fault isolation method of a hybrid HVDC system based on the coordination of a fault current limiter and a DC circuit breaker[J]. Power System Protection and Control, 2020, 48(19): 119-127.

[5] 孙立明, 杨博. 蓄电池/超导混合储能系统非线性鲁棒分数阶控制[J]. 电力系统保护与控制, 2020, 48(22): 76-83.

SUN Liming, YANG Bo. Nonlinear robust fractional-order control of battery/SMES hybrid energy storage systems[J]. Power System Protection and Control, 2020, 48(22): 76-83.

[6] 白志轩, 肖先勇, 张逸, 等. 计及谐波视在功率的谐波源识别方法[J]. 电力系统自动化, 2017, 41(8): 1-15.

BAI Zhixuan, XIAO Xianyong, ZHANG Yi, et al. Identification method of harmonic source considering harmonic apparent power[J]. Automation of Electric Power Systems, 2017, 41(8): 11-15.

[7] 孙媛媛, 李树荣, 石访, 等. 含分布式谐波源的配电网多谐波源责任划分[J]. 中国电机工程学报, 2019, 39(18): 5389-5398, 5586.

SUN Yuanyuan, LI Shurong, SHI Fang, et al. Multiple harmonic source contribution determination in the active distribution network with distributed harmonic sources[J]. Proceedings of the CSEE, 2019, 39(18): 5389-5398, 5586.

[8] 李从善, 刘天琪, 李兴源, 等. 用于电力系统状态估计的WAMS/ SCADA混合量测数据融合方法[J]. 高电压技术, 2013, 39(11): 2686- 2691.

LI Congshan, LIU Tianqi, LI Xingyuan, et al. Data fusion method of WAMS/SCADA hybrid measurements in power system state estimation[J]. High Voltage Engineering, 2013, 39(11): 2686-2691.

[9] 赵洪山, 田甜. 基于自适应无迹卡尔曼滤波的电力系统动态状态估计[J]. 电网技术, 2014, 38(1): 188-192.

ZHAO Hongshan, TIAN Tian. Dynamic state estimation for power system based on an adaptive unscented Kalman filter[J]. Power System Technology, 2014, 38(1): 188-192.

[10] 张伟晨, 熊永新, 李程昊, 等. 基于改进VDCOL的多馈入直流系统连续换相失败抑制及协调恢复[J]. 电力系统保护与控制, 2020, 48(13): 63-72.

ZHANG Weichen, XIONG Yongxin, LI Chenghao, et al. Continuous commutation failure suppression and coordinated recovery of multi-infeed DC system based on improved VDCOL[J]. Power System Protection and Control, 2020, 48(13): 63-72.

[11] LIU Y, MELIOPOULOS A, SUN L, et al. Protection and control of microgrids using dynamic state estimation[J]. Protection and Control of Modern Power Systems, 2018, 3(4): 340-352.

[12] 韩斐, 杨洪耕. 基于复值独立分量分析的配电网谐波状态估计[J]. 电网技术, 2014, 38(11): 3173-3179.

HAN Fei, YANG Honggeng. Harmonic state estimation in power distribution network based on complex independent component analysis[J]. Power System Technology, 2014, 38(11): 3173-3179.

[13] BEIDES H M, HEYDT G T. Dynamic state estimation of power system harmonics using Kalman filter methodology[J]. IEEE Transactions on Power Delivery, 1991, 6(4): 1663-1670.

[14] 王艳, 臧天磊, 符玲, 等. 基于谐波源特征提取的电力系统动态谐波状态估计自适应方法[J]. 电网技术, 2018, 42(8): 2612-2619.

WANG Yan, ZANG Tianlei, FU Ling, et al. Adaptive method for dynamic harmonic state estimation in power system based on feature extraction of harmonic source[J]. Power System Technology, 2018, 42(8): 2612- 2619.

[15] ZHAO J, MILI L, GÓMEZ-EXPÓSITO A. Constrained robust unscented kalman filter for generalized dynamic state estimation[J]. IEEE Transactions on Power Systems, 2019, 34(5): 3637-3646.

[16] 李大路, 李蕊, 孙元章. 混合量测下基于UKF的电力系统动态状态估计[J]. 电力系统自动化, 2010, 34(17): 17-21.

LI Dalu, LI Rui, SUN Yuanzhang. Power system dynamic state estimation with mixed measurements based on UKF[J]. Automation of Electric Power Systems, 2010, 34(17): 17-21.

[17] 孙江山, 刘敏, 邓磊, 等. 基于自适应无迹卡尔曼滤波的配电网状态估计[J]. 电力系统保护与控制, 2018, 46(11): 1-7.

SUN Jiangshan, LIU Min, DENG Lei, et al. State estimation of distribution network based on AUKF[J]. Power System Protection and Control, 2018, 46(11): 1-7.

[18] ZHAO J, MILI L. Robust unscented Kalman filter for power system dynamic state estimation with unknown noise statistics[J]. IEEE Transactions on Smart Grid, 2019, 10(2): 1215-1224.

[19] 孙国强, 黄蔓云, 卫志农, 等. 基于无迹变换强跟踪滤波的发电机动态状态估计[J]. 中国电机工程学报, 2016, 36(3): 615-623.

SUN Guoqiang, HUANG Manyun, WEI Zhinong, et al. Dynamic state estimation for synchronous machines based on unscented transformation of strong tracking filter[J]. Proceedings of the CSEE, 2016, 36(3): 615-623.

[20] 肖润龙, 王刚, 徐晨, 等. 含脉冲负载的中压直流综合电力系统的无迹卡尔曼动态状态估计方法[J]. 中国电机工程学报, 2020, 40(23): 7555-7566.

XIAO Runlong, WANG Gang, XU Chen, et al. An unscented Kalman filter based dynamic state estimation for the medium-voltage DC integrated power system with pulse load[J]. Proceedings of the CSEE, 2020, 40(23): 7555-7566.

[21] 陈碧云, 李弘斌, 李滨. 伪量测建模与AUKF在配电网虚假数据注入攻击辨识中的应用[J]. 电网技术, 2019, 43(9): 3226-3236.

CHEN Biyun, LI Hongbin, LI Bin. Application research on pseudo measurement modeling and AUKF in FDIAs identification of distribution network[J]. Power System Technology, 2019, 43(9): 3226-3236.

[22] 陆继翔, 张琪培, 杨志宏, 等. 基于CNN-LSTM混合神经网络模型的短期负荷预测方法[J]. 电力系统自动化, 2019, 43(8): 131-137.

LU Jixiang, ZHANG Qipei, YANG Zhihong, et al. Short-term load forecasting method based on CNN-LSTM hybrid neural network model[J]. Automation of Electric Power Systems, 2019, 43(8): 131-137.

[23] JAIN S K, JAIN P, SINGH S N. A fast harmonic phasor measurement method for smart grid applications[J]. IEEE Transactions on Smart Grid, 2017, 8(1): 493-502.

[24] 欧朱建, 程新功, 宗西举, 等. 电网谐波状态估计中的可观性分析[J]. 电力系统自动化, 2015, 39(6): 53-59.

OU Zhujian, CHENG Xingong, ZONG Xiju, et al. Observability analysis of power grid harmonic state estimation[J]. Automation of Electric Power Systems, 2015, 39(6): 53-59.

[25] 彭显刚, 潘可达, 张丹, 等. 基于季节性负荷自适应划分及重要点分割的多分段短期负荷预测[J]. 电网技术, 2020, 44(2): 603-613.

PENG Xiangang, PAN Keda, ZHANG Dan, et al. Piecewise short-term load forecasting based on adaptive seasonal load category and important point segment[J]. Power System Technology, 2020, 44(2): 603-613.

[26] SHU Q, WU Y, XU F, et al. Estimate utility harmonic impedance via the correlation of harmonic measurements in different time intervals[J]. IEEE Transactions on Power Delivery, 2020, 35(4): 2060-2067.

Dynamic harmonic state estimation of an unscented Kalman filter based on long short-term memory neural networks

HUANG Manyun, WANG Tianhao, WEI Zhinong, SUN Guoqiang

(College of Energy and Electrical Engineering, Hohai University, Nanjing 211100, China)

The Kalman filter prediction step of traditional dynamic harmonic state estimation usually constructs the state space model with a unit matrix and assumes the system noise covariance matrix as a constant matrix. This reduces the accuracy of the estimation and affects the results of the dynamic state estimation model. In order to establish the spatial model of harmonic state accurately, this paper proposes a time series prediction method based on a long short-term memory network. The complex state transfer process is simulated by off-line training of a large number of historical data, and the harmonic state at the present moment is predicted based on the filtering estimation of historical moments. This effectively improves the accuracy of the prediction model in an unscented Kalman filter. The method in this paper is tested and analyzed on the improved IEEE 34-node three-phase unbalanced system. Compared with the traditional method, the results show that the proposed method performs better in both precision and robustness of harmonic state estimation.

dynamic harmonic state estimation; unscented Kalman filter; long short-term memory neural networks;prediction model; robustness

10.19783/j.cnki.pspc.211221

国家自然科学基金项目资助(U1966205)；中央高校基本科研业务费专项资金项目资助(B200201067)

This work is supported by the National Natural Science Foundation of China (No. U1966205).

2021-09-03；

2021-12-13

黄蔓云(1991—)，女，博士，青年副教授，主要研究方向为电力系统运行与控制；E-mail: hmy_hhu@yeah.net

王天昊(1998—)，男，硕士研究生，主要研究方向为电力系统状态估计；E-mail: hhuwth@163.com

卫志农(1962—)，男，通信作者，博士，教授，博士生导师，研究方向为电力系统运行分析与控制、输配电系统自动化等。E-mail: wzn_nj@263.net

(编辑 葛艳娜)