计及虚拟惯量控制的DFIG等效惯量在线评估与响应特性分析

王彤，邢其鹏，李鸿恩，王增平

计及虚拟惯量控制的DFIG等效惯量在线评估与响应特性分析

王彤，邢其鹏，李鸿恩，王增平

(新能源电力系统国家重点实验室(华北电力大学)，北京 102206)

虚拟惯量控制的引入提高了双馈风机的频率调节能力，然而其惯量表现形式依赖于不同控制方式，导致其惯量响应特性不尽相同，亟需实现对其惯量水平及变化特征的准确感知。对基于转子动能虚拟惯量控制的双馈风机等效惯性定量表征及响应特性问题展开研究。首先，基于利用转子动能的虚拟惯量控制策略，建立了双馈风机在转子转速时间尺度下的简化模型，进而理论推导了双馈风机等效惯性常数的数学解析式。其次，针对解析式中双馈风机控制参数的“黑箱”问题，提出了一种基于自适应扩展卡尔曼滤波的控制参数在线辨识方法。在此基础上，利用双馈风机稳态运行下的量测信息在线评估双馈风机等效惯性常数，定量表征双馈风机的惯量支撑能力。最后，在改进的四机两区仿真系统上验证了该方法的准确性。仿真分析结果表明：虚拟惯量控制参数主要影响惯量响应过程的初始阶段和恢复阶段，速度控制器参数主要影响惯量响应过程的恢复阶段和稳定阶段。

双馈风机；虚拟惯量控制；等效惯量；控制参数；自适应扩展卡尔曼滤波；惯量响应特性

0 引言

在碳达峰、碳中和的时代背景下，加快构建以新能源为主体的新型电力系统是电力行业的必由之路。发展风电是实现国家能源战略，兑现国际承诺的重要举措[1-3]。作为风电市场的主要机型，双馈风机(Doubly-fed Induction Generator, DFIG)灵活快速的控制特性使其转子动能与输出有功功率相对解耦，基本不具备惯量支撑能力[4]。随着风电机组渗透率的提高，电力系统整体惯量水平势必会被削弱，严重恶化系统抗扰能力和稳定特性[4]。我国最新发布的《电力系统安全稳定导则GB38755-2019》中明确要求新能源场站应具有足够的惯量支撑能力。

目前，虚拟惯量控制技术[5-6]已成为提高电力系统惯量水平的重要手段，在DFIG传统控制策略的基础上将电网频率偏差相关量引入变流器有功控制环节，通过吸收或释放转子动能来抵抗电网频率波动，进而向电网提供惯量支撑。DFIG惯量响应特性与变流器类型、控制方式和机组运行工况息息相关[2]。含虚拟惯量控制的DFIG接入电网后，系统惯量不再是无法改变的固有特性，其时空变化特征将愈加突出，扰动后的惯量响应过程将会更加复杂多变，这使得传统电网的惯量分析技术的局限性日益凸显。

电力系统的惯量评估问题作为当前的研究热点[7-8]，可为电网规划和调度运行提供科学参考，对提高电力系统抗扰能力意义重大。根据评估方法分类，可分为以下两类：基于摇摆方程原理的评估方法[9-13]和基于准稳态运行数据的机器学习方法[14-15]。基于摇摆方程原理的评估方法是指根据扰动引起的功率不平衡量、频率变化率以及惯性时间常数之间的数学关系来计算获取惯量，具体可分为以下几种方式：基于系统在频率事件后的功率偏差和频率变化率的量测数据直接计算等效惯量[9-10]、根据摇摆方程推导机电振荡模态与等效惯量间的数学表达式，提取机电振荡特征参数实现等效惯量在线评估[11-12]、结合摇摆方程与参数辨识技术，从中提取惯量响应环节进而对等效惯量进行估计[13]。然而，基于摇摆方程原理的评估方法一般需要外加扰动信号，无法结合稳态运行下的量测信息对等效惯量实施在线跟踪和连续监测。针对此问题，基于准稳态运行的惯量评估方法[14-15]对历史数据中的等效惯量及频率波动进行相关性分析，构建含有等效惯量的学习模型，利用准稳态下的频率量测数据实时评估惯量。然而，上述评估方法大多聚焦于整个系统或部分区域的等效惯量，关于DFIG自身惯量及响应特性的研究[16-17]相对较少。一般情况下，同步机组的惯性时间常数已经给定，且其数值基本不会发生变化。但对于DFIG来说，其惯性响应特性较为复杂，对系统整体惯性的时空分布特性影响较大。而系统暂态稳定以及暂态失稳模式不仅与系统总惯性相关，与整个系统的惯性分布更为相关[18]。准确评估含虚拟惯量控制的DFIG自身等效惯量、深入分析其惯量响应特性可以为风电机组虚拟惯量的合理分配提供科学依据，有利于调度运行人员掌握系统惯量的时空分布情况，进而为实际系统安全预警和实时紧急控制策略提供理论参考。

本文对含虚拟惯量控制的DFIG等效惯性定量表征及响应特性问题展开研究。首先，在转子转速时间尺度下建立了计及锁相环和比例微分虚拟惯量控制的DFIG模型；然后，结合DFIG等效惯性常数的数学定义式，推导了DFIG等效惯性常数在此模型下的数学频域解析式；同时利用自适应扩展卡尔曼滤波(Adaptive Extended Kalman Filter, AEKF)参数辨识技术来获取DFIG等效惯性常数解析式中的控制参数；在此基础上，结合DFIG稳态运行下的量测数据计算其等效惯性常数，并根据等效惯性常数的变化特征，分析了虚拟惯量控制和速度控制器的控制参数对DFIG惯量响应过程各阶段的影响。

1 含虚拟惯量控制的DFIG模型

1.1 DFIG转子转速尺度暂态模型

多时间尺度控制是DFIG并网系统的关键特征，转子转速时间尺度[19]可用于该时间尺度下的储能元件(转子)的动态特性研究，适合于利用转子动能的虚拟惯量响应特性分析。因此，为了更加清晰和有针对性地解决DFIG等效惯量评估问题，本文建立了DFIG在转子转速时间尺度下的简化模型，并做出如下假设：

1) 忽略磁链的动态变化以及定子电阻损耗；

2) 不考虑风速和机械转矩的变化；

3) 电流内环控制响应速度远快于转子转速尺度，认为转子电流快速跟踪指令值[19]；

4) 网侧变流器相对于转子侧变流器动态较小，所以忽略网侧变流器动态[19]；

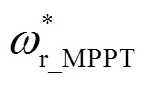
转子侧变流器控制通过定子电压定向矢量控制实现，由转子电流控制的电磁转矩方程为

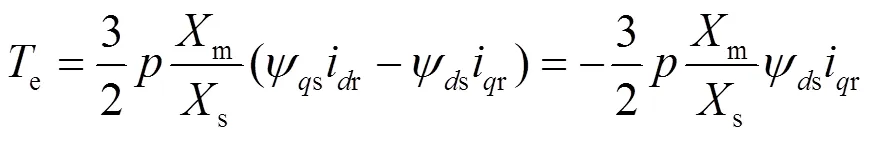
不考虑机械转矩的变化，转子运动方程增量频域表达式为

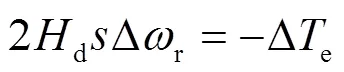
1.2 锁相环模型

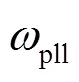
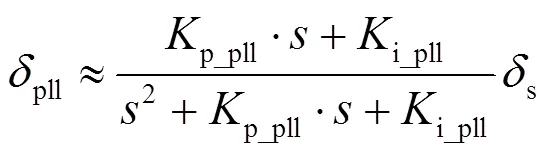
式中：为锁相环输出的相角；与为锁相环的积分与比例增益；为定子电压相角。

1.3 虚拟惯量控制模型

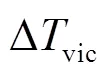
1.3.1基于锁相环频率的比例微分虚拟惯量控制

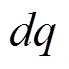
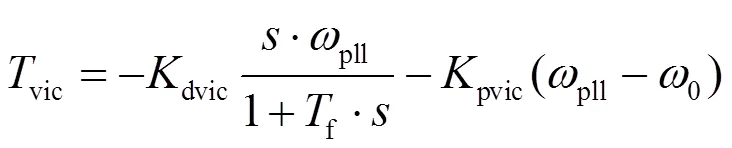
1.3.2最大功率追踪模块

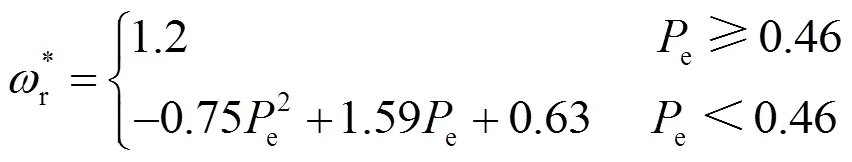
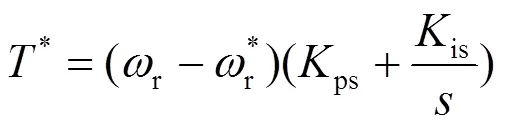
由式(3)、式(4)和式(6)联立可得电磁转矩参考值的增量表达式，如式(7)所示。

1.4 含虚拟惯量控制的DFIG简化模型

根据前述分析，含虚拟惯量控制的DFIG在转子转速尺度下的DFIG简化模型如图2所示，主要计及发电机暂态模型、传动链模型、锁相环模型、比例微分虚拟惯量控制、MPPT控制与速度控制器。

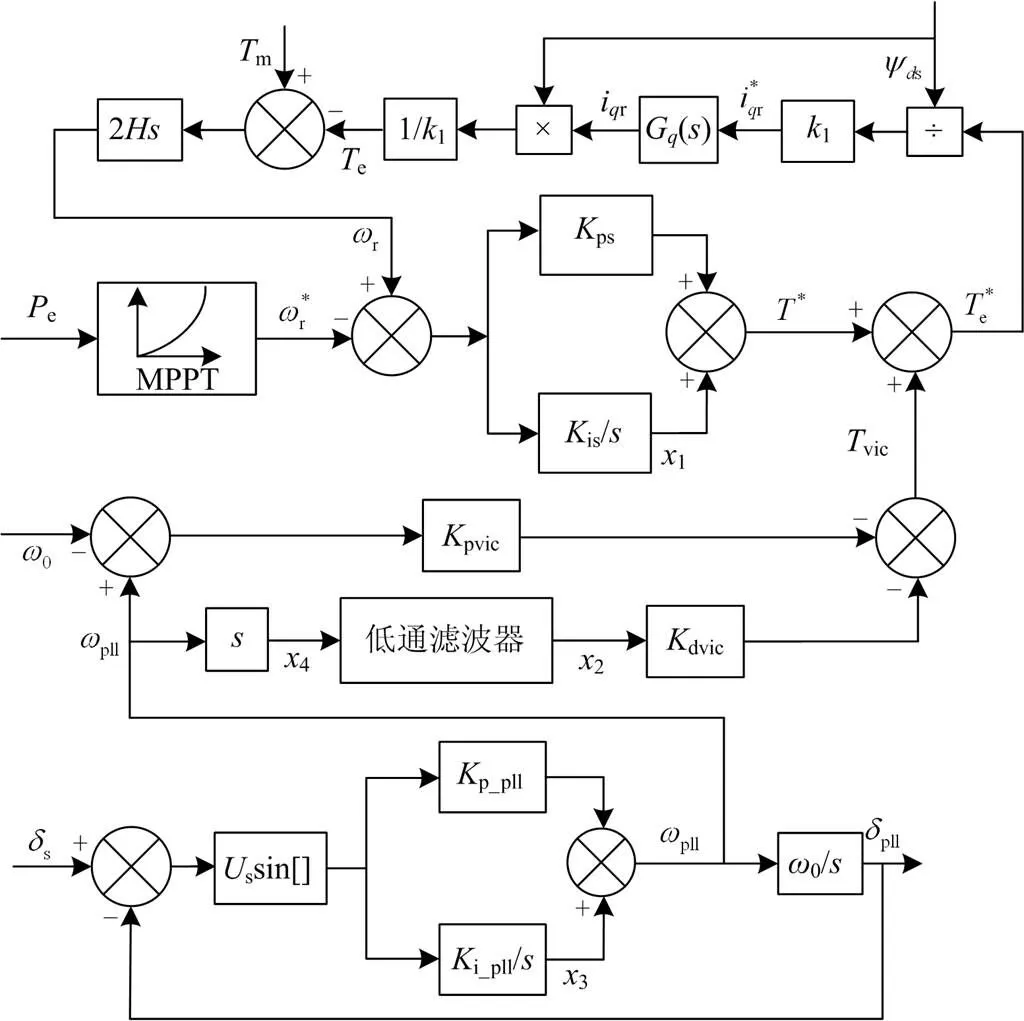
图2 含虚拟惯量控制的DFIG模型

2 含虚拟惯量控制的DFIG等效惯性常数

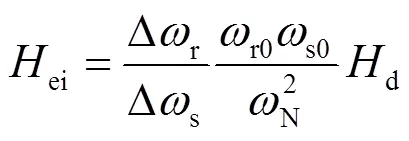
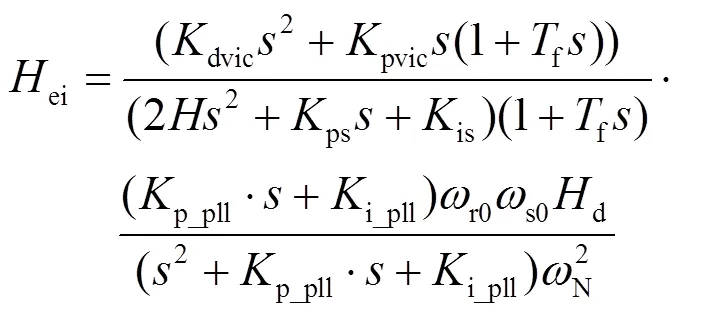
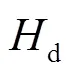
需要说明的是，本文针对一种给定的基于转子动能虚拟惯量控制的DFIG模型展开研究，进而分析其惯量响应特性。而如今新能源厂家众多、型号多样，通用化建模难度巨大，实际应用中很难完全匹配本文的控制结构。但是对于利用转子动能进行虚拟惯量控制的DFIG来说，其等效惯量大小均可以采用如式(8)所示的DFIG等效惯性常数定义式来定量表征。因此，随着新能源控制结构及其性能标准化、规范化发展，在已知DFIG具体模型和控制结构的条件下，完全可以采用本文所述的研究思路和理论方法来分析此类虚拟惯量控制下的DFIG惯量响应问题。

3 基于AEKF的DFIG控制参数辨识方法

扩展卡尔曼滤波EKF[24-25]是一种非线性最小方差估计，具有收敛速度快、抗干扰性强和估计精度高的优点。本文针对风电场信息量测的噪声对辨识精度的影响，在传统的EKF算法基础上引入Sage-Husa估值器自适应技术，通过估计随机噪声的统计特征来提高控制参数的辩识精度。

根据前文分析，用于AEKF的状态方程和量测方程为

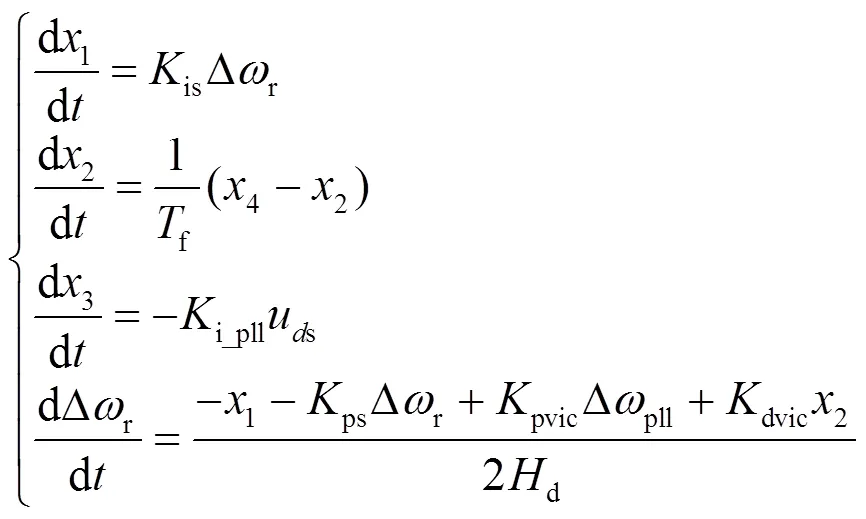
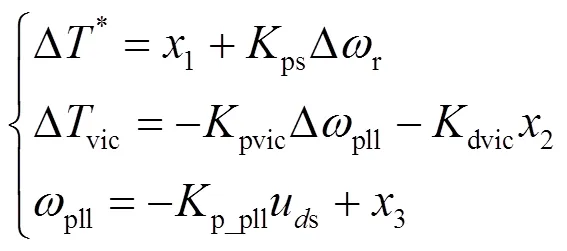
EKF作为常用的一种经典的非线性估计方法，在许多领域具有广泛的应用，其具体步骤可参见文献[24]。根据DFIG的数学模型和Sage-Husa估值器自适应技术，AEKF方法的主要步骤如下所述。

1) 预测更新

状态变量预测如式(12)所示。

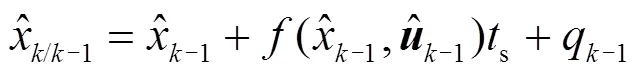
误差协方差矩阵预测如式(13)所示。

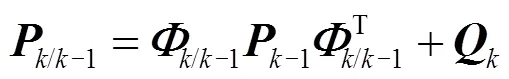
2) 增益矩阵和测量更新

增益矩阵计算如式(14)所示。

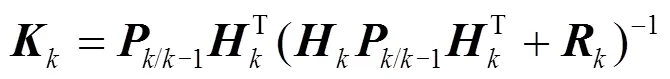
误差协方差矩阵更新为

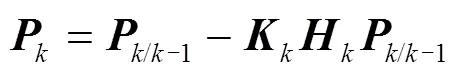
状态变量更新为

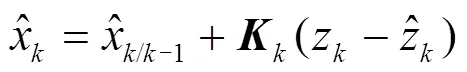
3) 随机噪声评估

采用Sage-Husa估计器对过程噪声协方差和量测噪声协方差进行实时估计，在迭代过程中对随机噪声进行自适应化地处理，以提高辨识精度。有偏噪声估计可以防止滤波发散，但会造成较大的估计误差，因此本文采用了将无偏噪声估计和有偏噪声估计相结合的方法，其计算方程式为

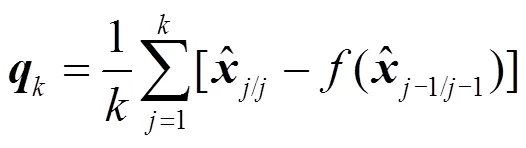
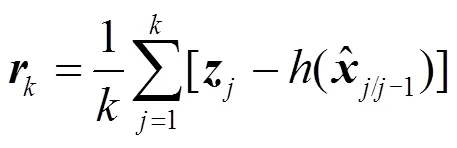
有偏噪声估计为

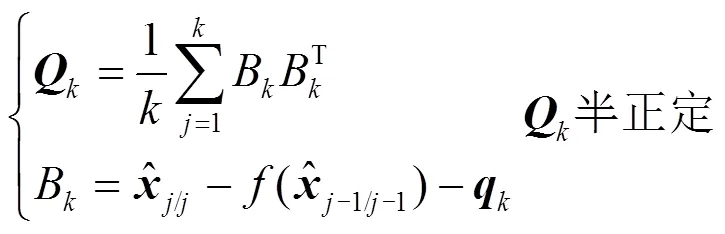
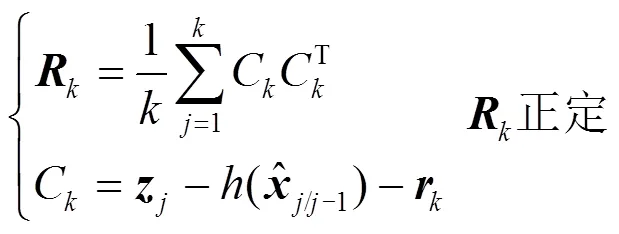
无偏噪声估计为

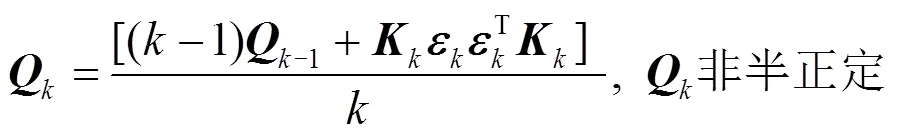
通过上述步骤不断迭代可以获得DFIG的控制参数，若风机控制参数不再发生变化，此后仅需风电场的实时量测信息和风机具体参数即可计算DFIG的等效惯性常数，摆脱了对大扰动事件的依赖。但是有时风电场模型参数需要改变[26]，当风机控制方式发生变化时，则需利用扰动后的量测数据重新在线辨识DFIG的控制参数。DFIG等效惯量评估方法的完整流程示意图如图3所示。

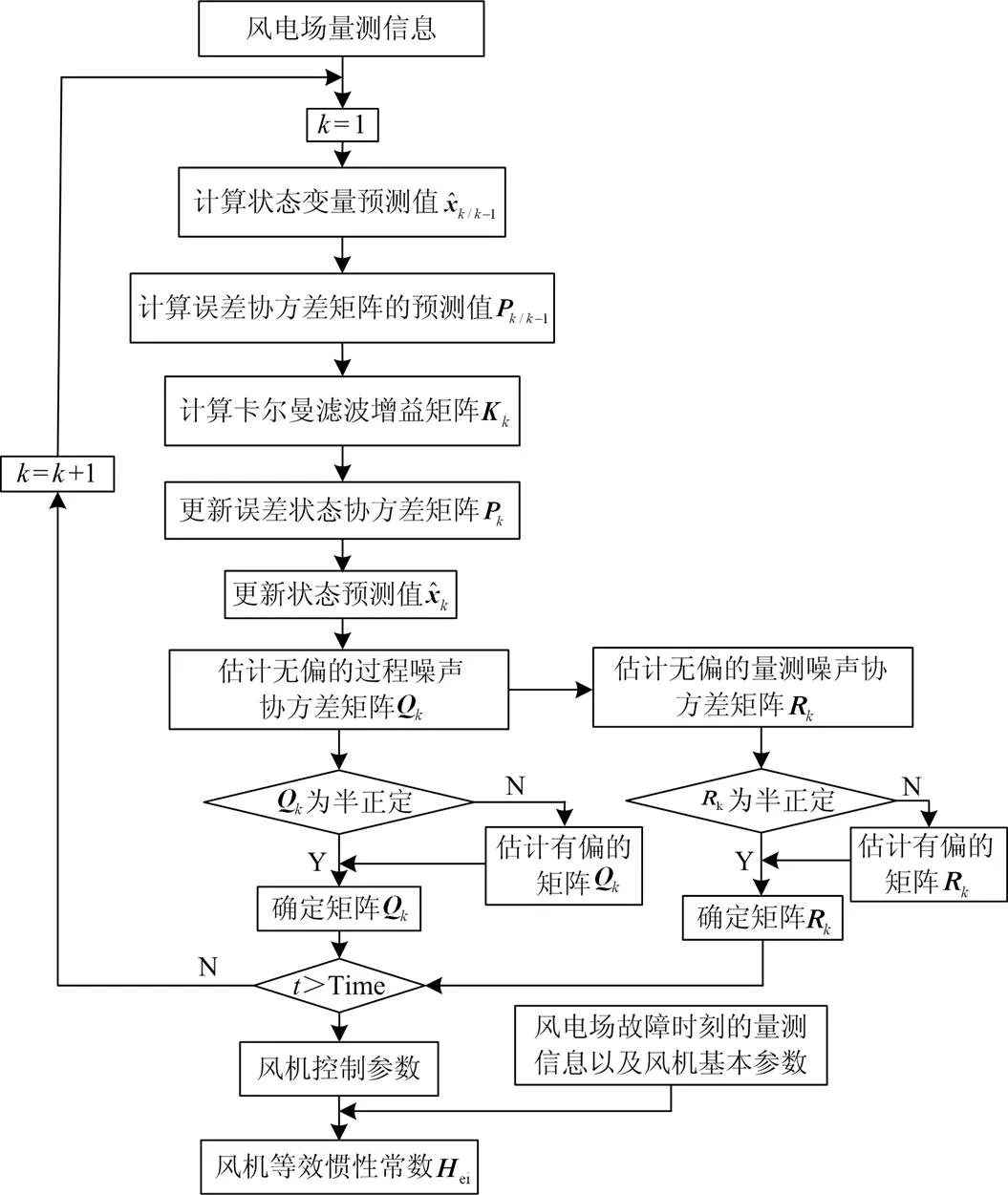
图3 DFIG等效惯量评估方法的流程示意图

4 仿真分析

改进的四机两区仿真系统如图4所示，DFIG替换节点1的同步机，利用Matlab平台验证上述辨识方法和等效惯量评估方法的准确性，并进一步探究控制参数对DFIG等效惯量的影响。

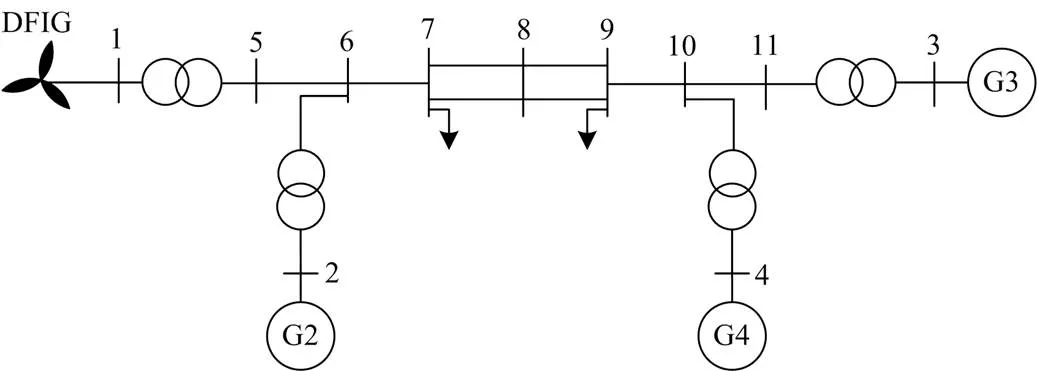
图4 改进的四机两区系统

4.1 基于AEKF的控制参数辨识结果

为了提高辨识结果的准确性，本文基于仿真数据采用试错法[27]来确定系统噪声协方差矩阵，测量噪声协方差矩阵采用对角元为的对角矩阵。时，在系统中施加三相短路故障，持续时间为0.1 s，仿真时间为10 s，仿真步长为0.01 s，将仿真结果得到的真值叠加高斯白噪声作为量测量。图5展示了辨识过程中控制参数不断迭代变化的曲线，表1给出了最终的详细辨识结果。

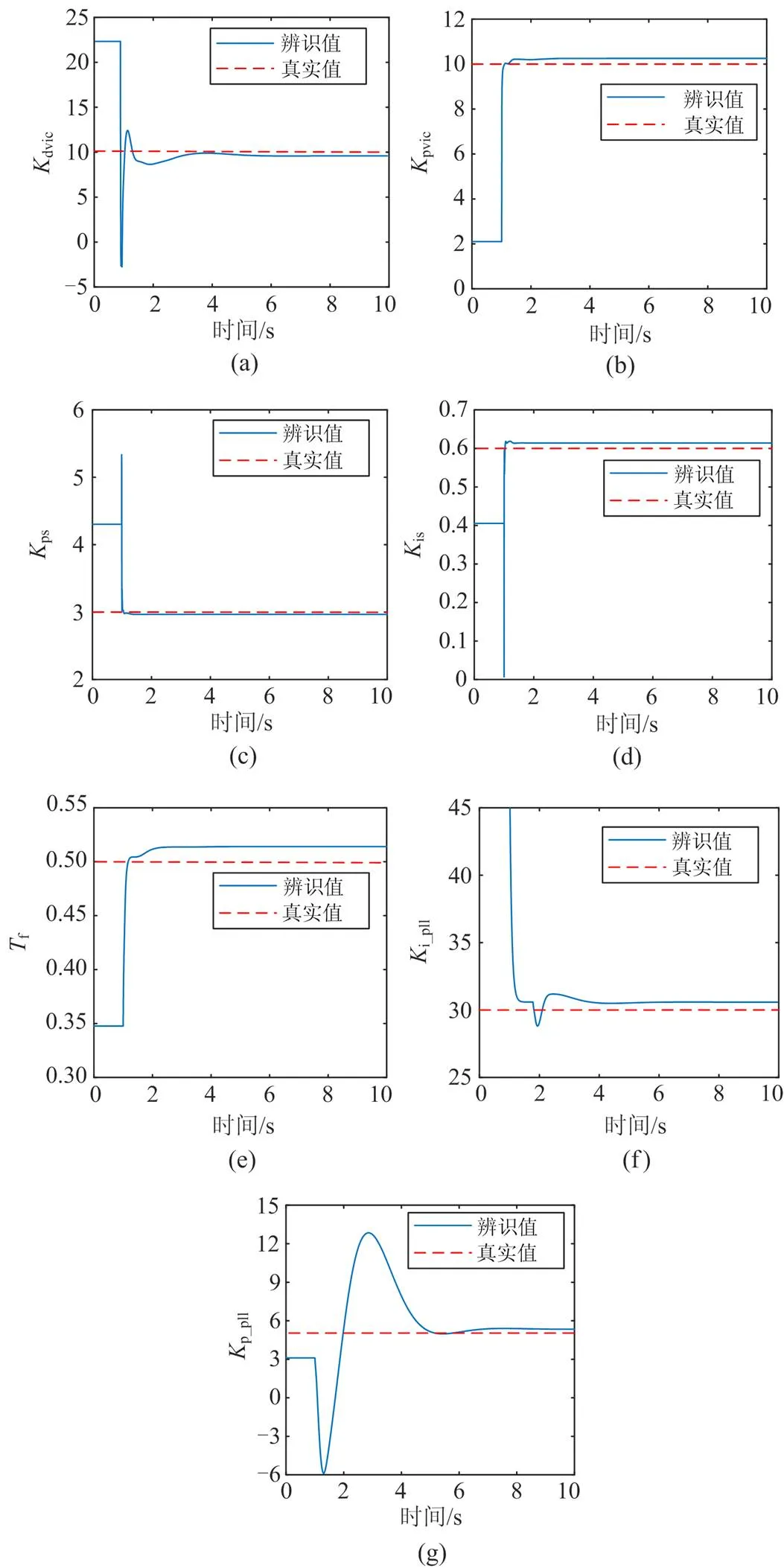
图5 控制参数的辨识结果曲线

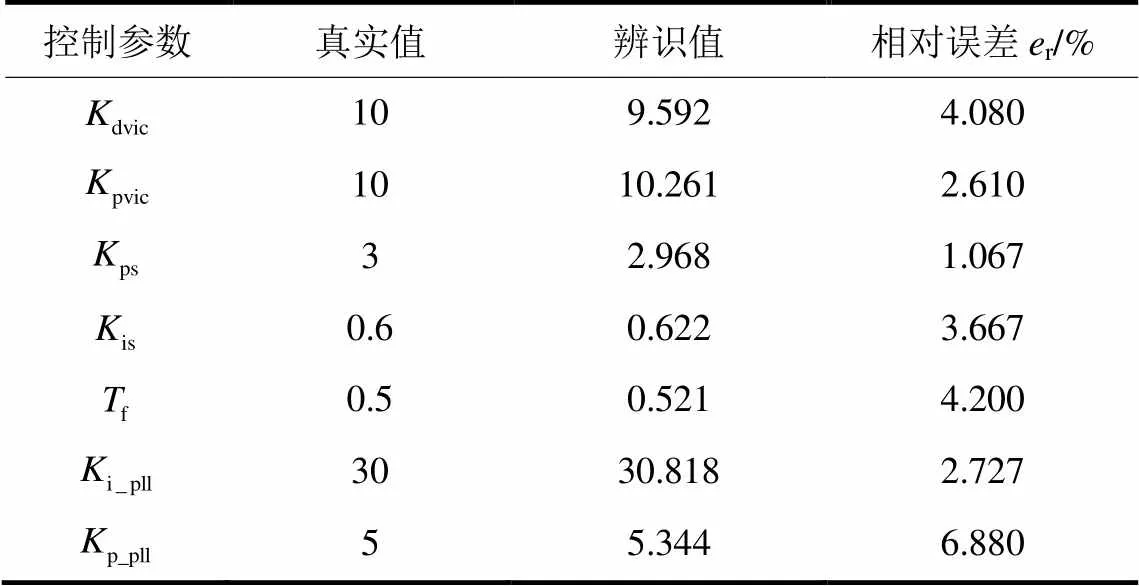
表1 控制参数辨识结果

由图5和表1的辨识结果可以看出，AEKF方法可以准确地辨识DFIG的控制参数，辨识结果存在的误差均在可接受的范围内，这为接下来DFIG等效惯性常数的评估奠定了基础。

4.2 DFIG等效惯量在线评估

图6 不同工况下两种算法的Hei对比结果

4.3 控制参数对DFIG等效惯性常数的影响分析

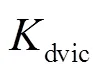
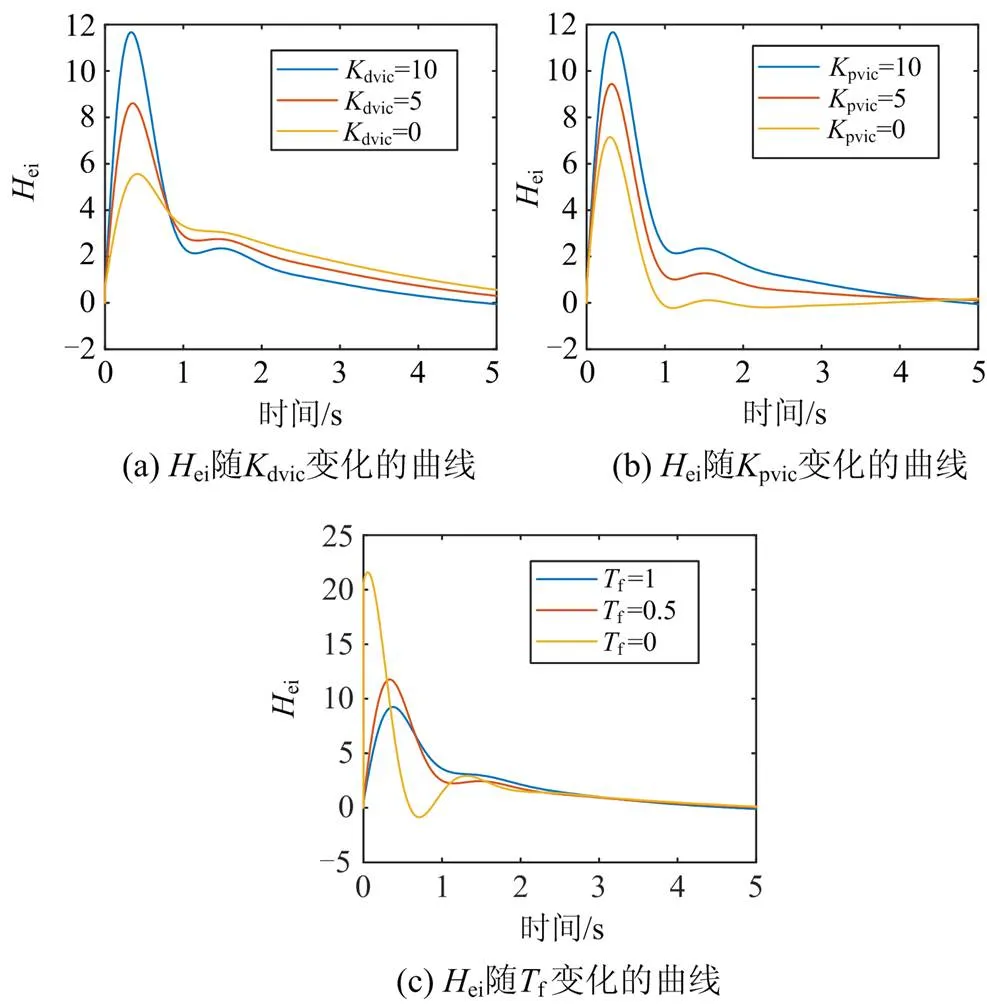
图7 虚拟惯量控制参数对的影响

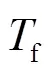
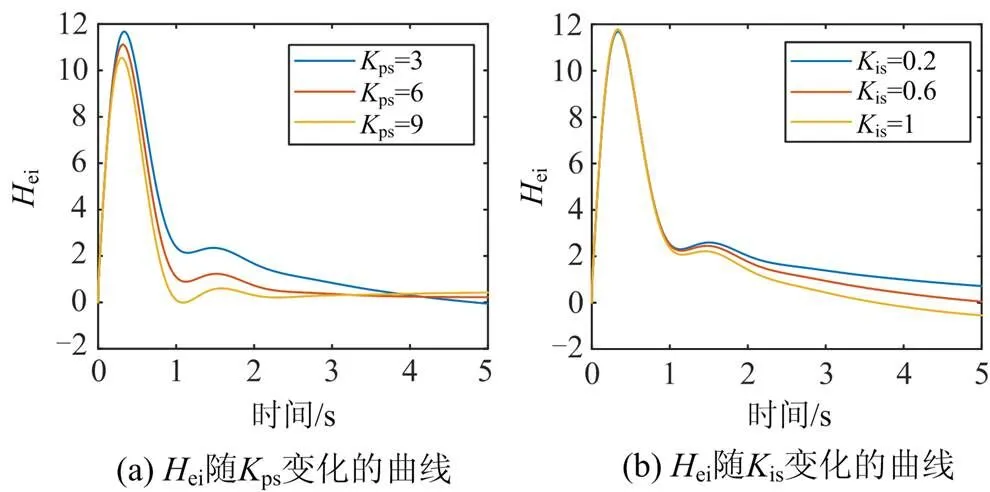
图8 速度控制器控制参数对的影响

综上所述，虚拟惯量控制参数主要影响惯量响应过程的初始阶段和恢复阶段，速度控制器参数主要影响惯量响应过程的恢复阶段和稳定阶段。虚拟惯量控制和速度控制器两者共同作用，直接决定了DFIG的惯量响应特性。

5 结论

本文对含虚拟惯量控制的DFIG等效惯量在线评估问题进行研究，主要内容可分为以下几个方面。

1) 构建了计及锁相环和虚拟惯量控制的DFIG转子转速时间尺度下的暂态模型；在此模型基础上，结合惯性常数的数学定义式，推导得到了DFIG等效惯性常数的数学解析式。

2) 针对风机控制参数的“黑箱”问题，提出了一种基于自适应扩展卡尔曼滤波的控制参数在线辨识方法；在获取到风机参数后，根据DFIG等效惯性常数的数学解析式，仅需风机稳态运行下的输出功率和电网频率的量测信息即可对DFIG的等效惯性进行实时计算。

3) 根据DFIG等效惯性常数的变化特征，分析了虚拟惯量控制和速度控制器的控制参数对DFIG惯性响应特性的影响。虚拟惯量控制参数主要影响惯量响应过程的初始阶段和恢复阶段，速度控制器参数主要影响恢复阶段和稳定阶段。

[1] 赵福林, 俞啸玲, 杜诗嘉, 等. 计及需求响应的含大规模风电并网下电力系统灵活性评估[J]. 电力系统保护与控制, 2021, 49(1): 42-51.

ZHAO Fulin, YU Xiaoling, DU Shijia, et al. Assessment on flexibility of a power grid with large-scale wind farm integration considering demand response[J]. Power System Protection and Control, 2021, 49(1): 42-51.

[2] 李德鑫, 宗崇林, 黄大为, 等. 大规模风电汇聚外送的区域送端电力系统两级优化调度[J]. 电力系统保护与控制, 2021, 49(11): 35-44.

LI Dexin, ZONG Chonglin, HUANG Dawei, et al. Two-level optimal dispatching of regional sending-end power system for large-scale clustering wind power transmission[J]. Power System Protection and Control, 2021, 49(11): 35-44.

[3] LI J, LIU C, ZHANG PF, et al. Difference between grid connections of large-scale wind power and conventional synchronous generation[J]. Global Energy Interconnection, 2020, 3(5): 486-493.

[4] 王同森, 程雪坤. 计及转速限值的双馈风机变下垂系数控制策略[J]. 电力系统保护与控制, 2021, 49(9): 29-36.

WANG Tongsen, CHENG Xuekun. Variable droop coefficient control strategy of a DFIG considering rotor speed limit[J]. Power System Protection and Control, 2021, 49(9): 29-36.

[5] 张雪娟, 束洪春, 孙士云, 等. 双馈风机参与系统调频对系统暂态功角稳定性的影响分析[J]. 电力系统保护与控制, 2021, 49(2): 18-29.

ZHANG Xuejuan, SHU Hongchun, SUN Shiyun, et al. Effect analysis of a doubly-fed induction generator participating in system frequency modulation on system transient power angle stability[J]. Power System Protection and Control, 2021, 49(2): 18-29.

[6] 彭喜云, 刘瑞叶. 变速恒频双馈风力发电机辅助系统调频的研究[J]. 电力系统保护与控制, 2011, 39(11): 56-61.

PENG Xiyun, LIU Ruiye. Research on the frequency regulation of aiding system of VSCF double-fed wind generator[J]. Power System Protection and Control, 2011, 39(11): 56-61.

[7] 张武其, 文云峰, 迟方德, 等. 电力系统惯量评估研究框架与展望[J]. 中国电机工程学报, 2021, 41(20): 6842-6856.

ZHANG Wuqi, WEN Yunfeng, CHI Fangde, et al. Research framework and prospect on power system inertia estimation[J]. Proceedings of the CSEE, 2021, 41(20): 6842-6856.

[8] 王博, 杨德友, 蔡国伟. 高比例新能源接入下电力系统惯量相关问题研究综述[J]. 电网技术, 2020, 44(8): 2998-3006.

WANG Bo, YANG Deyou, CAI Guowei. Review of research on power system inertia related issues in the context of high penetration of renewable power[J]. Power System Technology, 2020, 44(8): 2998-3006.

[9] AZIZIPANAH-ABARGHOOEE R, MALEKPOUR M, PAOLONE M, et al. A new approach to the online estimation of the loss of generation size in power system[J]. IEEE Transactions on Power Systems, 2019, 34(3): 2103-2113.

[10] WALL P, TERZIJA V. Simultaneous estimation of the time of disturbance and inertia in power systems[J]. IEEE Transactions on Power Delivery, 2014, 29(4): 2018-2031.

[11] CAI G, WANG B, YANG D, et al. Inertia estimation based on observed electromechanical oscillation response for power systems[J]. IEEE Transactions on Power Systems, 2019, 34(6): 4291-4299.

[12] PANDA R K, MOHAPATRA A, SRIVASTAVA S C. Online estimation of system inertia in a power network utilizing synchrophasor measurements[J]. IEEE Transactions on Power Systems, 2020, 35(4): 3122-3132.

[13] ZHANG J, XU H. Online identification of power system equivalent inertia constant[J]. IEEE Transactions on Industrial Electronics, 2017, 64(10): 8098-8107.

[14] TUTTELBERG K, KILTER J, WILSON D, et al. Estimation of power system inertia from ambient wide area measurements[J]. IEEE Transactions on Power Systems, 2018, 33(6): 7249-7257.

[15] CAO X, STEPHEN B, ABDULHADI I F, et al. Switching Markov Gaussian models for dynamic power system inertia estimation[J]. IEEE Transactions on Power Systems, 2015, 31(5): 3394-3403.

[16] 刘皓明, 任秋业, 张占奎, 等. 双馈风机等效惯性时间常数计算及转差率反馈惯量控制策略[J]. 电力系统自动化, 2018, 42(17): 49-57.

LIU Haoming, REN Qiuye, ZHANG Zhankui, et al. Calculation of equivalent inertia time constant for doubly-fed induction generators and slip-feedback inertia control strategy[J]. Automation of Electric Power Systems, 2018, 42(17): 49-57.

[17] LIU M, CHEN J, MILANO F. On-line inertia estimation for synchronous and non-synchronous devices[J]. IEEE Transactions on Power Systems, 2021, 36(3): 2693-2701.

[18] 赵振元, 陈维荣, 戴朝华, 等. 系统惯性时间常数对互联电网暂态稳定水平的影响[J]. 电网技术, 2012, 36(1): 102-107.

ZHAO Zhenyuan, CHEN Weirong, DAI Chaohua, et al. Influence of system inertia time constants on transient stability level of interconnected AC power grid[J]. Power System Technology, 2012, 36(1): 102-107.

[19] 唐王倩云, 张睿, 胡家兵. 用于系统暂态行为分析的双馈风机转子转速控制时间尺度暂态模型[J]. 中国电机工程学报, 2021, 41(9): 3037-3046.

TANG Wangqianyun, ZHANG Rui, HU Jiabing. Modelling of DFIG-based WT for power system transient responses analysis in rotor speed control timescale[J]. Proceedings of the CSEE, 2021, 41(9): 3037-3046.

[20] LIU J, TANG F, ZHAO J, et al. Coherency identification for wind-integrated power system using virtual synchronous motion equation[J]. IEEE Transactions on Power Systems, 2020, 35(4): 2619-2630.

[21] 应杰. 基于幅相运动方程的双馈风电机组机电尺度建模与特性分析及对电力系统稳定影响[D]. 武汉: 华中科技大学, 2018.

YING Jie. Modeling and characteristics analysis of doubly fed induction generator based wind turbine in electromechanical time-scale based on amplitude-phase motion equations method and its impact on power system stability[D]. Wuhan: Huazhong University of Science and Technology, 2018.

[22] CLARK K, MILLER N W, SANCHEZ-GASCA J. Modeling of GE wind turbine-generators for grid studies[R]. Schenectady: GE Energy, 2010.

[23] 李世春, 邓长虹, 龙志君, 等. 风电场等效虚拟惯性时间常数计算[J]. 电力系统自动化, 2016, 40(7): 22-29.

LI Shichun, DENG Changhong, LONG Zhijun, et al. Calculation of equivalent virtual inertial time constant of wind farm[J]. Automation of Electric Power Systems, 2016, 40(7): 22-29.

[24] 陈振, 刘向东, 靳永强, 等. 采用扩展卡尔曼滤波磁链观测器的永磁同步电机直接转矩控制[J]. 中国电机工程学报, 2008, 28(33): 75-81.

CHEN Zhen, LIU Xiangdong, JIN Yongqiang, et al. Direct torque control of permanent magnet synchronous motors based on extended Kalman filter observer of flux linkage[J]. Proceedings of the CSEE, 2008, 28(33): 75-81.

[25] 柴林杰, 蔡亦浓, 高铭, 等. 基于加权平均插值和容积卡尔曼滤波的配电网预测辅助状态估计[J]. 电力建设, 2021, 42(8): 1-9.

CHAI Linjie, CAI Yinong, GAO Ming, et al. A forecasting aided state estimation for distribution network based on weighted average interpolation and cubature Kalman filter[J]. Electric Power Construction, 2021, 42(8): 1-9.

[26] 杨睿茜, 陈红坤, 陶玉波, 等. 双馈式风机控制器参数整定的实用方法[J]. 电力系统保护与控制, 2015, 43(2): 63-69.

YANG Ruixi, CHEN Hongkun, TAO Yubo, et al. A practical method on doubly-fed induction generator controller parameter determination[J]. Power System Protection and Control, 2015, 43(2): 63-69.

[27] ZERDALI E. A comparative study on adaptive EKF observers for state and parameter estimation of induction motor[J]. IEEE Transactions on Energy Conversion, 2020, 35(3): 1443-1452.

Online evaluation and response characteristics analysis of equivalent inertia of a doubly-fed induction generator incorporating virtual inertia control

WANG Tong, XING Qipeng, LI Hong'en, WANG Zengping

(State Key Laboratory of Alternate Electric Power Systems with New Energy Resources (North China Electric Power University), Beijing 102206, China)

The introduction of virtual inertia controlimproves the frequency regulation ability of a DFIG. However, its manifestation of inertia depends on different control modes, resulting in different response characteristics. It is important to determine an accurate perception of its inertia level and change characteristics. In this paper, the quantitative characterization and response characteristics of the equivalent inertia of a DFIG based on virtual inertia control of rotor kinetic energy are studied. First, a simplified model of a DFIG in rotor speed timescale is established based on a virtual inertia control strategy utilizing rotor kinetic energy, and then the mathematical expression of equivalent inertia constant of the DFIG is derived theoretically. Secondly, given that there is a problem of unknown control parameters, an online evaluation method of control parameters based on adaptive extended Kalman filter is proposed. The equivalent inertia constant of the DFIG is calculated and the inertia support ability of the DFIG is quantitatively evaluated based on the measurement information of the DFIG in steady-state operation. Finally, the accuracy of the proposed method is verified on an improved 4-machine 2-area simulation system, and the simulation results show that the virtual inertia control parameters mainly affect the initial stage and recovery stage of the inertia response process, and the speed controller parameters mainly affect the recovery stage and stability stage of that process.

doubly fed induction generator; virtual inertia control; equivalent inertia; control parameters; adaptive extended Kalman filter; inertia response characteristics

10.19783/j.cnki.pspc.211029

国家自然科学基金重点项目资助(51637005)；新能源电力系统国家重点实验室开放课题资助(LAPS20021)

This work is supported by the National Natural Science Foundation of China (No. 51637005).

2021-08-04；

2021-12-07

王 彤(1985—)，女，通信作者，副教授，博士生导师，研究方向为新能源电力系统稳定分析与控制、暂态稳定分析与紧急控制；E-mail: hdwangtong@126.com

邢其鹏(1997—)，男，硕士研究生，研究方向新能源电力系统暂态稳定分析与控制；E-mail: xqpncepu@163.com

王增平(1964—)，男，教授，博士生导师，研究方向为继电保护、变电站综合自动化、广域保护等。E-mail: wangzp1103@sina.com

(编辑 周金梅)