基于灰色关联度分析的导水裂隙带高度预测

白丽扬

(1.吕梁学院 矿业工程系，山西 吕梁 033001；2.河南省瓦斯地质与瓦斯治理重点实验室 省部共建国家重点实验室培育基地，河南 焦作 454003；3.吕梁市智慧煤矿工程技术研究中心，山西 吕梁 033001)

煤层采出后，采空区上覆岩层从下往上会出现岩层的垮落、岩层中出现裂缝、岩层发生弯曲变形等现象，有时候也会出现离层带，一旦这些裂缝和断裂互相沟通后就会形成导水通道。根据“上三带”理论[1-3]，将变形和破坏后的煤层覆岩划分为三带，即：垮落带、裂隙带和弯曲下沉带，垮落带和裂隙带又合称为导水裂隙带，如图1所示。导水裂隙带范围内的岩层失去了隔水性能，将会造成矿井涌水量的增加，不仅破坏了地下水资源，也威胁煤矿的安全开采，因而其发育高度的准确预测尤为重要。

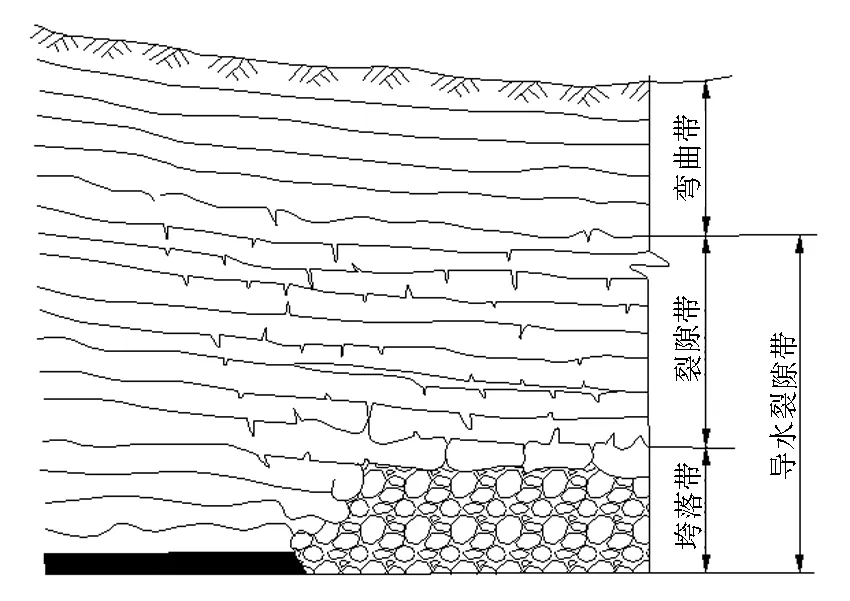
图1 “上三带”示意

国内外很多学者对导水裂隙带高度的预测进行了研究。寻博辉等[4]选取开采深度、倾角、开采厚度和工作面斜长作为导水裂隙带高度的主要影响因素，综合利用现场探测、数值计算和机器学习结合的方法，构建了适用于山西地区的导水裂隙带高度预测模型。施龙青等[5]对导高带的主要影响因素进行了分析，并通过理论计算得出含水层水压对导水裂隙带的发育也有一定的促进作用。娄高中等[6]针对BP神经网络收敛速度慢和容易陷入局部极小的问题，优化了BP神经网络模型的权值和阈值，建立了PSO-BP神经网络的导水裂隙带高度预测模型。张峰[7]等根据影响导水裂隙带高度的各影响因素之间的关系，应用正交试验法，设计了共18次试验，用3DEC数值模拟软件研究了特厚煤层综放工作面导水裂隙带的发育高度。

导高带的计算广泛采用“三下规程”的经验公式法，只考虑了采高一个影响因素，显然是不够全面的，这种方法适用于煤层埋藏深度不大的薄煤层工作面导水裂隙带高度的计算；目前，我国多数的矿井开采具有采深大、工作面跨度大、采厚大的特点，由于这些开采条件的变化导致现有的经验公式不再适用。因此本文在前人的研究基础上，进行大采深条件下导水裂隙带发育高度的预测研究。

1 大采深导水裂隙带高度预测模型

1.1 算法简介

LinearRegression是利用数理统计中的回归分析，来确定多个变量之间相互依赖的定量关系的一种统计方法。它利用最小二乘函数对一个或多个自变量和一个标量型因变量之间的关系进行建模，如果模型中只涉及1个自变量，称为简单线性回归，涉及多个自变量的则称为多元线性回归。

给定p维数据集{xi1,…xip,yi}(i=1,2…,N)，线性回归模型假设因变量yi和自变量xi之间是线性关系，即：

当p=1时，就表示为简单的一元线性回归：

yi=w0+w1xi

假设yi的方差为常数，回归系数w0和w1对应直线在纵轴的截距和斜率，则可以使用下式来计算：

1.2 导水裂隙带高度影响因素分析

为了对大埋深(采深>400 m)下导水裂隙带发育高度进行研究，选取采深、硬岩岩性比例系数、采高和工作面斜长为主要影响因素，调研和收集了导水裂隙带高度实测数据共41组，其中用38组数据建模，剩余的3组数据进行模型的检验，部分建模数据如表1[8-9]所示。

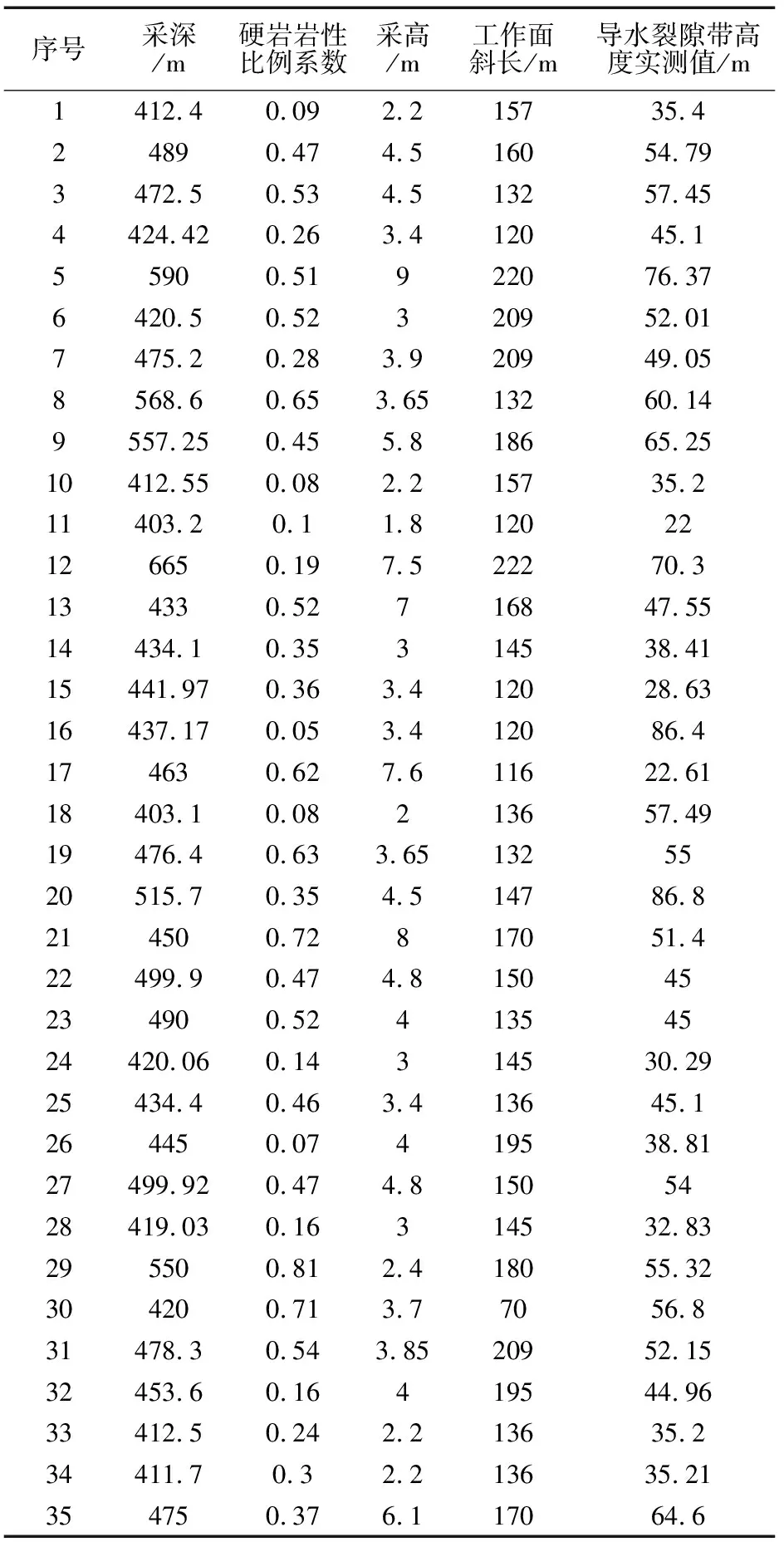
表1 建模数据

1)采深。根据矿山压力控制理论可知，在一定范围内，开采深度越大，矿山压力就越大，矿山压力的大小和煤层的开采深度成正比，所以开采深度越大，顶板岩层的运动越剧烈，导水裂隙带高度也越发育。

2) 硬岩岩性比例系数。硬岩岩性比例系数能够较综合地反映煤层顶板和上覆岩层强度及结构组合等特点，而且该系数的获得比较方便。

3) 采厚。随着煤层开采厚度的增加，上覆岩层的塑性区也变大，造成垮落带的高度也越大，而且在“三下”规程导水裂隙带高度的经验公式计算中，采厚是唯一的参数，是由此可见，开采厚度决定着垮落带的高度。

4) 工作面斜长。煤层在没有达到充分采动之前，导水裂隙带的发育高度随着工作面的开采逐渐增加；当煤层充分采动之后，工作面斜长对导高带的发育影响则不明显。

1.3 灰色关联度分析

1.3.1 初值化序列生成

数理统计的分析方法往往需要大量的样本数据，否则就很难找出统计规律，灰色关联分析方法弥补了数理统计方法的缺憾，对样本数据量少同样适用，而且计算量也不大[10]。

不同影响因素序列可能存在着量纲不同的情况，为了消除这种差异，需要通过无量纲化处理，即通过数学变换来消除原始变量量纲影响的一种方法，初值化算子、均值化算子和区间值化算子都可以使系统行为序列无量纲化，本文采用初值化算子，变换后数据见表2。

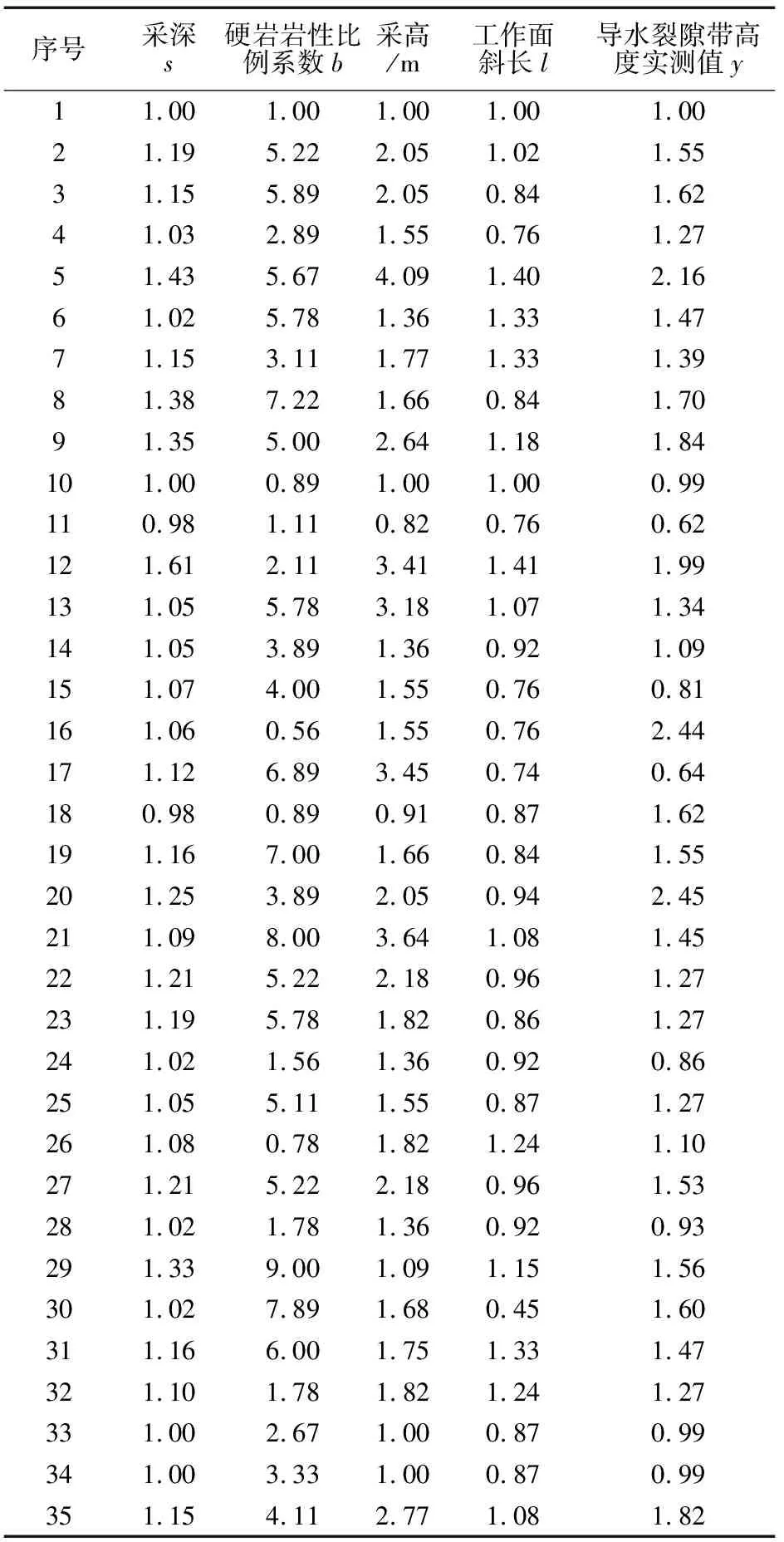
表2 初值变换序列

1.3.2 灰色关联度计算

1) 求关联系数。

式中，γ0i(k)为关联系数；m为两级最小差；M为两级最大差；ξ为相关系数，一般取0.5。

经过计算得出，两级最小差为0，最大差为7.437。

2) 计算关联度。对每个因素序列的各关联系数求取算数平均值：

灰色关联度计算结果如表3所示，可以得出，开采深度、硬岩岩性比例系数、开采厚度、工作面斜长的灰色关联度依次为：0.92、0.61、0.87、0.90，说明各影响因素对导水裂隙带高度的影响程度重要性排序为采深>工作面斜长>采高>硬岩岩性比例系数。

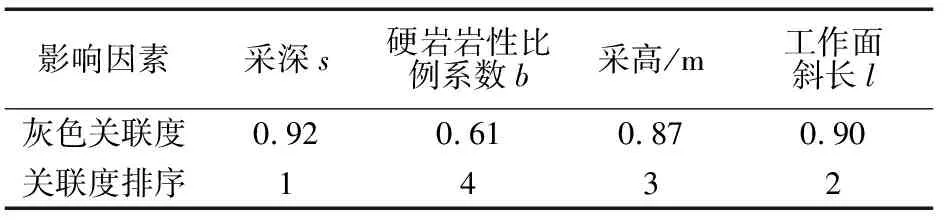
表3 灰色关联度结果

1.4 预测结果对比分析

将上述建模数据另存为arff格式文件，模型的评估方法选择训练集评估，再选择LinearRegression算法进行训练，最后将运行结果保存；“三下”规程中的经验公式[11]只考虑了采高对导水裂隙带高度的影响，具体计算公式见表4。式中：Hf为导水裂隙带高度，M为开采厚度。两种模型所得出的导水裂隙带高度的预测值和真实值曲线见图2，两种计算方法的绝对误差和相对误差结果见表5。

表4 导水裂隙带高度“三下”规程经验公式

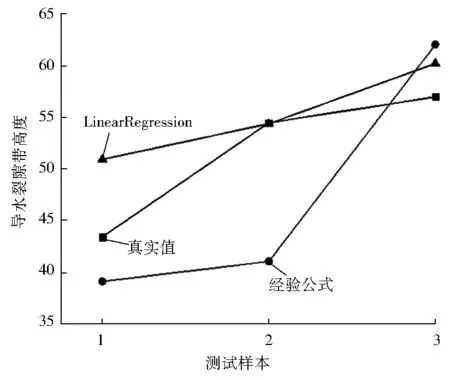
图2 预测模型曲线

表5 经验公式和LinearRegression模型预测结果

1) 通过表5的计算分析可以得出，大埋深条件下，“三下”规程中的经验公式的最大绝对误差为13.44 m，相对误差最大值为24.66%，LinearRegression模型的最大绝对误差为7.52 m，相对误差最大值为17.31%，且相对误差的最小值仅为0.18%.

2) 平均相对误差越小，说明模型的精度越高，预测性能越好。“三下”规程中的经验公式的平均相对误差为14.51%；LinearRegression模型的平均相对误差为7.73%，LinearRegression模型的平均相对误差比经验公式提升了6.78%，预测结果更接近实际值，适用于大采深条件下导水裂隙带高度的预测。

2 结 语

1) 基于灰色关联度分析方法完成了对导水裂隙带高度影响因素的关联分析，得出，各影响因素对导水裂隙带高度的影响程度重要性排序为采深>工作面斜长>采高>硬岩岩性比例系数。

2) “三下”规程经验公式的平均相对误差为14.51%，LinearRegression模型的平均相对误差为7.73%，LinearRegression模型的平均相对误差比经验公式提升了6.78%，预测结果更接近实际值，精度更高，可以为大埋深下导水裂隙带高度的预测提供参考。