基于矩阵法的曲柄连杆机构运动学分析

林 瑾

(无锡商业职业技术学院，江苏 无锡 214153)

引 言

机械设计是机械生产的第一步.一部机器质量的优劣，首先取决于设计质量，而在机械设计环节中工作量最大、最重要的是机械结构设计[1].机械结构设计需要综合考虑机械产品的工作性能、使用要求、制造成本、材料性能等因素，只有这样才能在诸多限定条件下设计出最优性能的机械.但有些因素之间会产生互相矛盾，比如，工作性能与使用要求、制造成本与材料性能等，因此，设计过程中不能将各方面因素作片面化分析.为了使机械产品性能达到较高水平，必须深入探讨每一个设计环节，对于复杂、多解的设计方案，需要不断修改、优化和完善，这些都离不开机构分析和机构综合[2].

机构分析和机构综合常用的方法有图解法和解析法.进行传统设计时，图解法用得较多，但此方法作图复杂且精度不高.随着现代计算机辅助设计和优化设计的发展，解析法的应用越来越广泛，其可将机构的位置、速度、加速度等问题转化为数学问题来解决.机构的结构参数、运动参数也可使用数学解析式来进行描述，以便于在机械设计时，进行深入分析，确保设计的科学性[3-4].

解析法设计时，常用矩阵理论作为处理数据的工具，以解决计算工作量过大的难题.应用矩阵作为工具对机构进行解析法分析时，可将机构当作一个质点系，对于机构中的运动副以杆长作为约束条件，建立非线性方程组，从而求解出机构的各点位置，进而可以对速度和加速度进行分析求解[5].

1 运动分析基础

以平面连杆机构为例，分析机构运动情况，确定机构运动特性.将平面连杆机构用一种特殊的图形来描述，把机构中的各个构件当做图形的边界，运动副当做是图形的顶点.将机构用图形来描述后，图形中的边界和顶点可以用矩阵来表示，比如，平面图形中，可以用点的坐标或者向量的坐标作为矩阵的参数值：

利用坐标值可进行平面连杆机构的位移分析，建立位移方程，这是平面连杆机构运动分析的基础，其涉及非线性方程的计算[6].在位移方程的基础上对时间求一阶导数，可以得到速度方程，求二阶导数，可以得到加速度方程，这些都是线性方程.

2 平面四杆机构运动分析

图1所示是常见的平面四杆机构ABCD，以运动副A所在位置为原点建立直角坐标系，x轴沿着杆AD的方向.根据矩阵在机构中的应用，先用矢量法建立机构的位置方程.

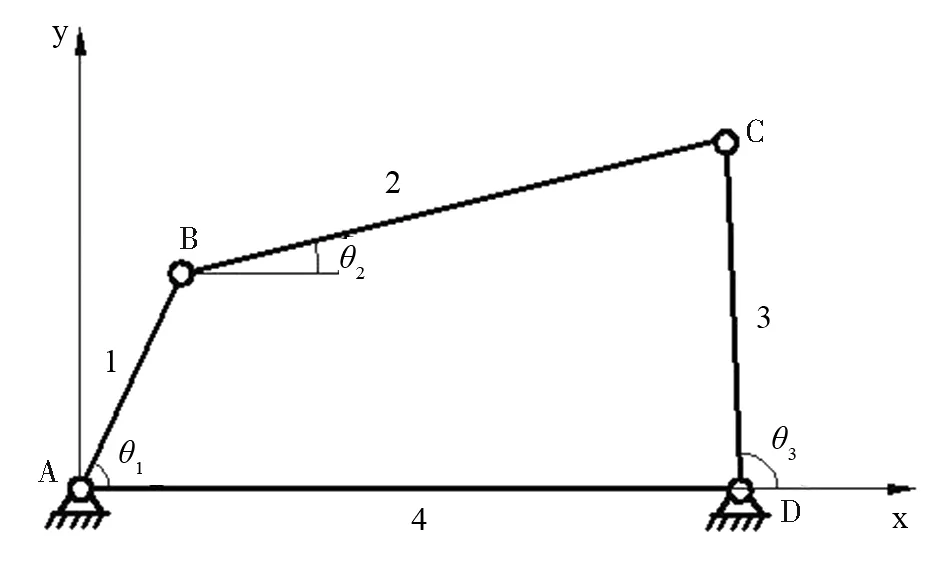
图1 平面四杆机构

设四根构件的长度分别为l1、l2、l3和l4，构件的方位角度为θ1、θ2、θ3和θ4.杆4沿着x轴的方向，因此θ4=0.四杆件组成封闭的矢量多边形，矢量和等于零，封闭矢量表达式为：

(1)

以封闭矢量表达式为依据，位置方程的分量形式可写成：

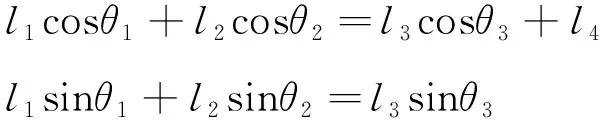
(2)

从式(2)的x轴和y轴分解向量中，可以求得方位角度的代数式，由此描述各杆件的位置.位置方程可用矩阵形式表示为：

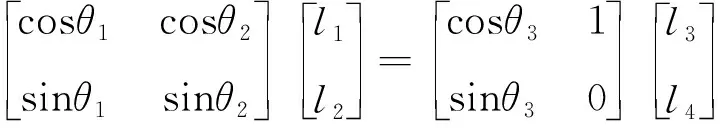
(3)

式(2)闭环矢量方程分量形式对时间求一阶导数，就可得到平面四杆机构的速度方程：

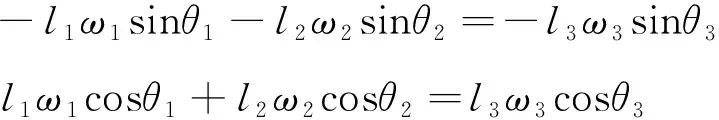
(4)

由式(4)可求解出各从动杆的角速度，从而为机构的运动学分析提供数据支持.

若需要使用计算机来分析机构的速度及加速度情况，可将式(4)用矩阵形式进行描述.为了表述时更加清晰，将机构中原动件杆1的参数置于矩阵等式右侧，将从动件杆2和从动杆3的参数置于矩阵左侧，矩阵形式如下：

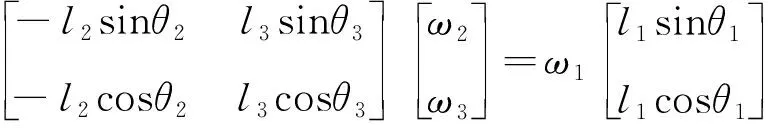
(5)

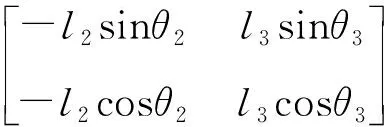
速度矩阵的表达式可简写为：[A][ω]=ω1[B]

(6)

为进一步分析机构的运动情况，可对式(5)继续求二阶导数，便可以得到如下平面四杆机构的加速度矩阵表达式：

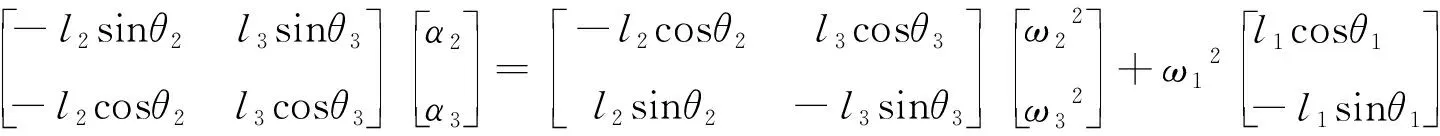
(7)

(8)

采用上述方式，可分析平面四杆机构中某个定点的运动情况，求出该点的位置方程、速度方程和加速度方程，从而计算出该点的速度和运动角度.

3 曲柄连杆机构运动分析

如图2所示，在往复式内燃机中，曲柄连杆机构是核心的传动机构，它是内燃机燃烧的场所.曲柄连杆机构可以将燃料燃烧后所产生的热能转化为机械能，完成能量转换.在做功行程中，曲柄连杆机构将活塞的往复运动转化为曲轴的旋转运动，对外输出动力.在进气、压缩和排气行程中，曲柄连杆机构将曲轴的旋转运动转化为活塞的往复直线运动，从而实现工作循环.

图2 曲柄连杆机构

曲柄连杆机构的工作条件十分恶劣，需要承受高温、化学腐蚀以及周期性变化的冲击载荷.如果在工作中，曲柄连杆机构出现故障，将会使发动机其他部件发生损坏，引发严重的安全事故.因此，曲柄连杆机构的结构设计和材料选用要求相当高，它的结构和性能直接影响发动机品质的优劣[7].

曲柄连杆机构由曲轴、连杆和活塞组成，分为中心式和偏心式两种.图3为曲柄连杆机构运动简图.图3(a)机构中心线经过了曲轴的旋转中心，这是中心式曲柄连杆机构，图3(b)机构中心与曲轴旋转中心偏离了一段距离，这是偏心式曲柄连杆机构.

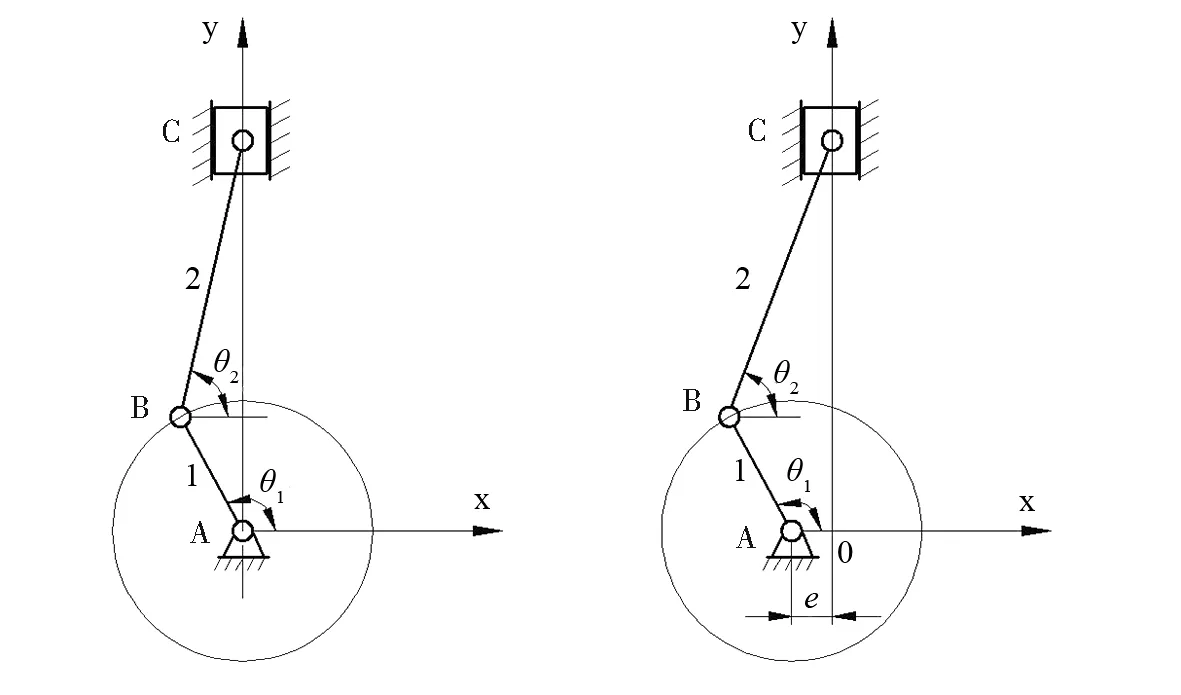
(a)中心式曲柄连杆机构 (b)偏心式曲柄连杆机构 图3 曲柄连杆机构运动简图

进气行程中，该机构通过曲轴1的匀速转动，带动连杆2转动，从而推动活塞C在移动副约束下，沿着设定的轨迹往复直线运动.用上述矩阵法分析曲柄连杆机构活塞C的运动情况，了解运动的具体行程和速度，可为曲柄连杆机构设计提供重要的参考数据.

3.1 位置分析

在图3的机构简图中，设定曲柄1和连杆2长度分别为l1、l2，对应方位角度为θ1、θ2.活塞运行方向与y轴重合，设定x轴正向为机构运动的起始轴线，机构转动的正方向为逆时针方向.

下文以偏心式曲柄连杆机构为例，描述进气行程中机构运动情况.由于偏心式曲柄连杆机构的内燃机中心线和曲轴的中心线不重合，故设定偏心距为e.

将偏心式曲柄连杆机构应用ABCO封闭图形来分析(O为C点在x轴上的投影)，封闭图形用矢量表达式可描述为：

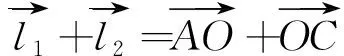
(9)

若AO沿着x轴正方向，OC沿着y轴正方向，由图形封闭性可得到该机构的位置方程为：

(10)

在式(10)中lAO和1、2杆的杆长均为固定值，由两个方程式可求得活塞C的运动轨迹和从动杆2的方位角.

3.2 速度分析

若需要分析曲柄连杆机构中活塞C的运动速度情况，可对式(10)求时间t的一阶导数，得速度方程如下：

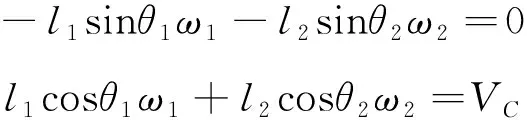
(11)

进气行程中，曲柄1为原动件，将其参数置于等式右侧，其余从动件参数置于等式左侧，得到速度矩阵为：

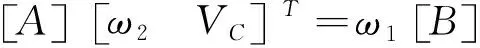
(12)

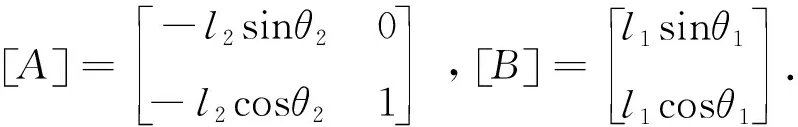
由式(12)可得知活塞C的速度，并可求得连杆2的角速度.

3.3 加速度分析

式(12)继续对时间t求一阶导数，可得加速度矩阵为：

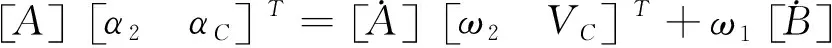
(13)

由式(13)可求得活塞C的加速度，并可求得连杆2的角加速度.

通过以上运动分析，可得到进气行程中连杆和活塞的运动参数，当需要对做功行程进行运动分析时，可参照以上方法进行推导.由矩阵分析得出的各项参数可为曲柄连杆机构的动力分析及强度校核提供数据支持.

4 曲柄连杆机构运动仿真

随着软件技术的发展，连杆机构的运动学仿真应用越来越普遍.在使用牛顿经典力学完整分析连杆机构的运动情况、建立矢量方程和矩阵后，可以很方便地应用计算机软件来建立连杆机构的仿真模型，从而对连杆机构的运动和工作情况进行仿真分析，模拟工作情况，预测工作性能.仿真分析可应用于连杆机构的设计阶段，可视化的结果有助于提高连杆机构的设计效率.

MATLAB 软件是一种交互式计算分析软件，该软件具有科学计算、程序设计、图形绘制等多种功能.利用该软件强大的矩阵运算分析功能，可在众多的数据中获取最优结果，轻松完成连杆机构的仿真分析过程，并有效提高连杆机构的设计水平和质量.

将上述曲柄连杆机构的矢量方程和矩阵用MATLAB 的计算工具来求值，结合其可视化手段，将计算值拟合成曲线，可得到曲柄连杆机构的运动仿真轨迹.

选取某一型号发动机参数如下：曲轴半径l1=57.5 mm，连杆长度l2=210 mm，活塞高度h=32.5 mm，曲轴偏移e=13 mm.

假定机架为参考系，曲柄与x轴重合，活塞行程设为s.非线性超越方程组如下：

(14)

根据式(14)创建函数crankshaft，其格式如下：

function t=crankshaft(th,th1,L1,L2,e)

t=[L1*cos(th1)+L2*cos(th(1))-e;L1*sin(th1)+L2*sin(th(1))-th(2)];

在MATLAB中应用软件自带的fsolve函数，调用上述crankshaft函数，可求解出连杆2对应方位角度θ2和活塞行程s，这部分运行程序如下：

th23(m,:)=fsolve('crankshaft',[1 1],options,th1(m),L1,L2,e)];

为了直观显示出相关参数，可利用MATLAB中plot命令来绘制连杆2运动仿真图形，绘图的程序如下：

plot([x;xx],[y;yy],'k',[0 L1],[0 0],'k--^',x,y,'ko',xx,yy,'ks')];

在上述程序完全运行后，绘制出连杆的运动仿真位置，如图4所示.从图4中可清楚了解连杆的运行路径，为运动过程分析提供基础数据.

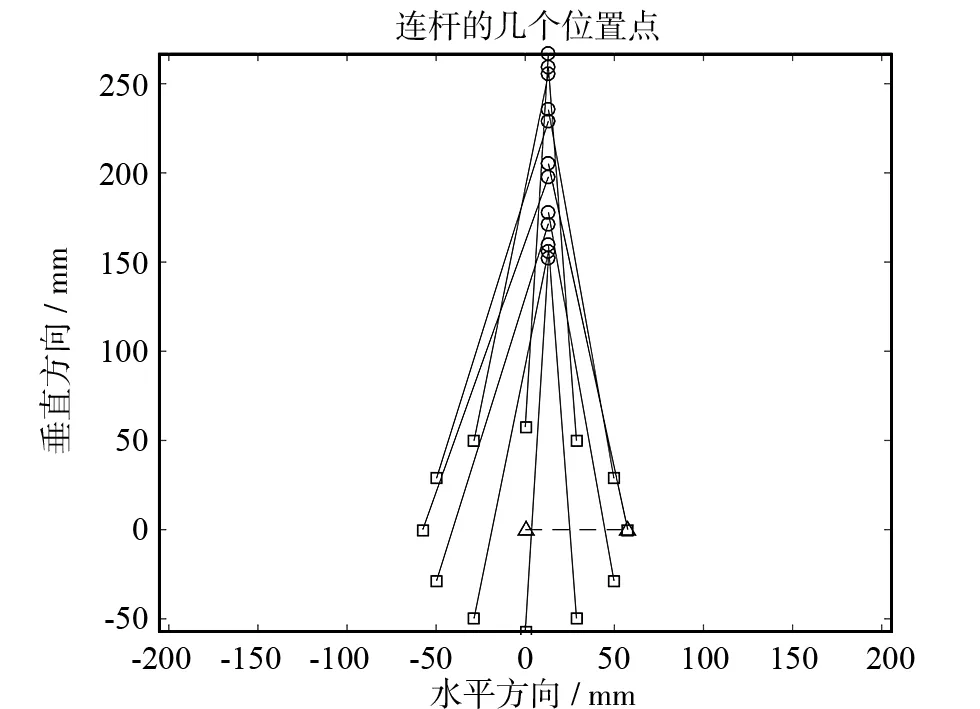
图4 连杆仿真位置

根据式(12)，可利用上述fsolve函数以及inv函数、plot命令绘制θ2和s的仿真曲线图，直观描述曲轴匀速转动时，连杆2对应方位角度θ2以及活塞行程s的变化情况，主要程序指令如下：

plot(th1,th23(:,1));

axis([0 2*pi 0 0.94*pi]);

w1=250;

for i=1:length(th1);

A=[-L2*sin(th23(i,1)) 0;-L2*cos(th23(i,1)) 1];

B=[w1*L1*sin(th1); w1*L1*cos(th1)];

w=inv(A)*B;

绘制出曲柄连杆机构中连杆的角位移仿真曲线图和活塞位移仿真曲线图，如图5和图6所示.

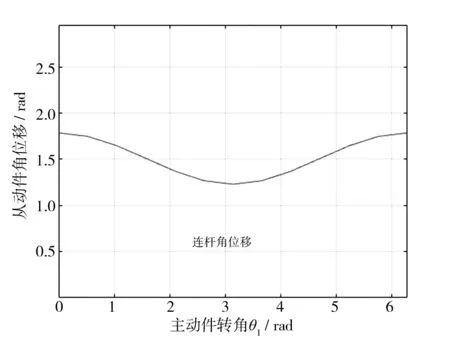
图5 连杆角位移仿真曲线图

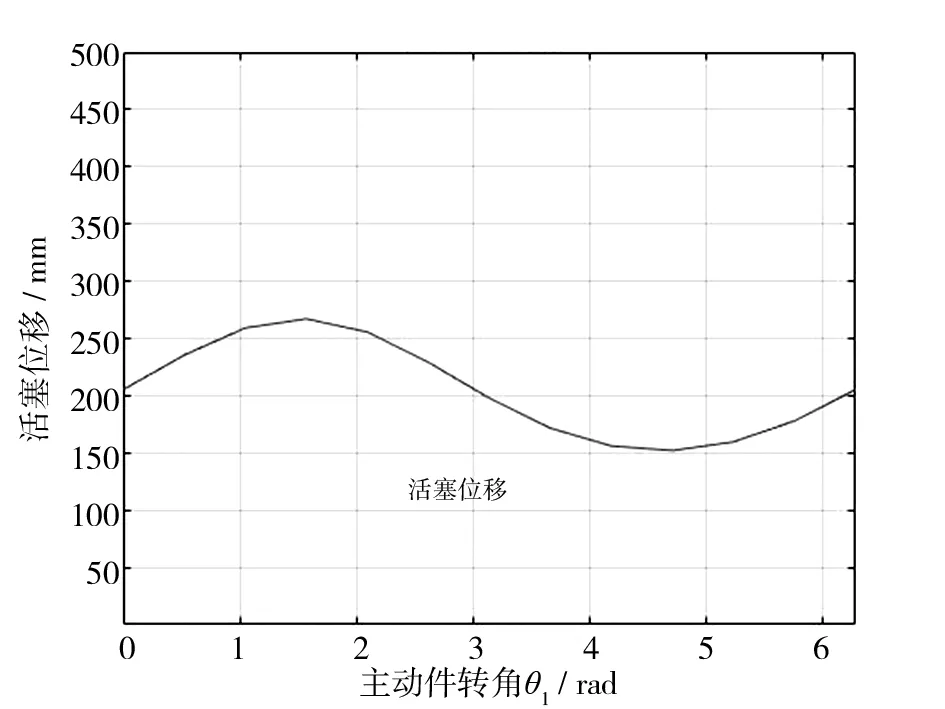
图6 活塞位移仿真曲线图

5 结论

矩阵可以表达构件的坐标位置，还可用于描述位移、速度、加速度等参数的变化情况.文中利用矩阵分析内燃机中曲柄连杆机构的运动学规律，先建立机构矢量方程，再通过矩阵获取活塞、连杆的位移、速度、加速度等运动参数，最后可将矢量方程和矩阵用计算机软件进行运动模拟，将机构的运动分析过程可视化，使设计结果更为直观.

实例分析表明，在曲柄连杆机构设计研究中，应用矩阵进行分析和运算，可以很方便地获取该机构的各种属性，分析过程简单易懂，同时，也使曲柄连杆机构的设计过程更为精确、可靠.在此基础上，利用计算软件辅助设计曲柄连杆机构，充分发挥了计算机强大的运算能力，提高了机械设计的质量和效率[8].当然，在对连杆机构以外的其他类型机构进行运动分析时，亦可引入合理的矩阵来描述连杆机构的内部信息.