六自由度机器人轨迹精度评定方法优化与补偿实验研究
尹宏杰,唐 尧
(1.杭州市质量技术监督检测院,浙江 杭州 310019;2.聚光科技(杭州)股份有限公司,浙江 杭州 310052)
引言
随着“中国制造2025”越来越多地实践和应用,智能制造扮演着越来越重要的角色,并且从加工逐步延伸到工业各个领域,作为典型的智能装备工业机器人的应用也更为广泛。随着工业机器人在市场应用中的难度和复杂程度逐渐的提升,对其末端运动轨迹精度提出了更高的要求[1]。
工业机器人重复定位精度较高,因此目前对提高工业机器人精度的研究主要集中在末端绝对定位精度[2-4]上,通过研究相关标定方法等建立误差模型,辨识参数及补偿修正;空间点位优化方法选取空间最优点位进行补偿;神经网络[5]预测补偿点位误差等提高机器人末端点位精度。而对机器人末端运动轨迹精度的研究方法大多停留在理论上,能够有效应用到实际工业当中的却很少,但也取得了相关的理论成果。Santolaria[6]等分析了温度对模型参数及对末端位置造成的影响,补偿误差参数提高其运动精度。Chettibil[7]从机器人最小能耗轨迹规划出发,约束机器人动力学中位移、速度、加速度、转矩等参数,采用三次样条曲线转化非线性优化问题进行研究。文献[8-9]采用遗传算法、提出基于距离轨迹的规划算法实现运动时间最优,精确运动到指定的空间轨迹。费家人[10]等考虑结构参数误差及关节转角偏差,基于ADAMS建立轨迹精度预测模型进行有效的轨迹精度预测。蔡锦达[11]等构建自适应模糊神经网络轨迹控制器,对机器人轨迹误差进行在线补偿。以上研究对提高机器人末端轨迹精度都有一定的效果,但很少从轨迹静态误差源因素出发建立综合轨迹精度模型,未对各误差源与机器人轨迹误差的关系作深入研究,且相关补偿方式在实际环境中因其理论方案的理想性、复杂性而采用较少。本文从上述问题出发,通过高精度的激光跟踪仪设备进行测量,构建机器人轨迹测量与补偿系统,对其运动轨迹进行轨迹精度的评定,为提高工业机器人的轨迹精度提供理论与实际依据。
1 轨迹精度模型
1.1 误差源分析
六自由工业机器人的轨迹误差分为静态误差与动态误差[12],静态误差即为机器人进行轨迹运动时不随时间发生变化,一般由加工制造、环境温度、关节间隙、传感器和控制系统等产生,其中主要体现为机器人结构参数a、d、α与机器人关节变量参数θ。结构参数中a、d的连杆长度误差ΔL为主要误差,关节扭角α为次要误差。动态误差即为机器人进行轨迹运动时随时间时刻发生变化的误差,一般由外力、惯性力及重力引起的振动与变形,其中主要体现为关节柔性误差即关节角误差和连杆柔性误差,连杆柔性误差由柔性变形、磨损等引起。综上六自由度工业机器人的轨迹误差中运动学误差大约占95%,而非几何误差占5%左右。
将各误差进行数学定义并将机器人的轨迹误差进行数学关系表达,连杆长度误差ΔL=ΔL1+ΔL2,ΔL2=LaiΔt,关节转角误差Δθ=Δθ1+Δθ2+Δθ3+Δθ4,,总误差ΔR=Δξ+Δη+Δζ。
式中:ΔL1为加工误差;ΔL1为温度引起的杆长变化;ai为连杆材料的热伸系数;Δt为温度变化量。Φd为电机转角误差,μ为电机与连杆间的传动比,Δθ1为电机控制误差引起,Δθ2为传动运动误差引起;Δθ3为传动机构间隙误差引起;Δθ4为关节柔性误差引起。Δξ为静态误差源引起的末端误差;Δη+Δζ为动态误差源引起的末端误差。
1.2 轨迹误差模型构造
从机器人位置误差模型进一步分析机器人轨迹误差模型,六自由度机器人通过建立各轴坐标系,以各杆之间的转换矩阵进行误差传递并表示出末端位置的矩阵形式即:
由于受到各误差源的影响,无论机器人是运动PTP轨迹还是CM轨迹,其末端均产生由误差影响的位姿变化量,即理论末端位置与实际末端位置的偏差即:
通过对机器人轨迹误差源的分析,运动学参数误差对机器人的位置精度影响最大,六自由度工业机器人通过建立常用DH模型引入连杆偏距a、连杆长度d、连杆扭角α和关节转角θ等运动参数分析在机器人运动过程中对轨迹的影响机理。若运动过程中产生运动偏差:
其中a、d、α为理论固定值,不考虑由其他误差源如环境温度等对运动参数的改变量,而关节转角θ为机器人正解过程的输入量,即机器人运动轨迹时在各个时刻的关节转角θ发生变化,对机器人设定轨迹在运动时间内受运动误差的影响从而导致实际轨迹与理论轨迹有一定的偏差,各运动参数产生的误差具体为:
机器人在笛卡尔空间坐标系下的理论轨迹函数,轨迹运动过程中受影响最大的运动参数误差后的实际轨迹与轨迹偏差函数表示为:
当误差较小时可对其进行微分线性化处理:
式中:∂a=∂ai,∂d=di,∂α=αi,∂θ=θi。
求解的运动学参数误差为:
因此得出六自由工业机器人轨迹精度模型的一般表示为:
式中:e为点位置误差值,M为目标轨迹采样前M个位置误差较大的点数。
2 机器人轨迹精度评定方法及优化
目前评定工业机器人轨迹精度的方法主要是根据国标ISO9283中相关机器人性能检测标准,其中对机器人轨迹精度评定主要是在机器人的工作空间内选取最大立方体,在立方体的对角线及其对角面上进行一定数量轨迹选取,依据指令轨迹上m个计算点的位置与n次测量的集群中心G间的距离最大值即:
已有的轨迹精度评定方法主要通过计算选取采样点的原轨迹理论点与实际轨迹中做正交面得到的实际点计算距离作为轨迹最大偏差值ATP,现考虑从点与点的距离转化为点到轨迹的距离偏差,计算各采样点到轨迹距离偏差进行轨迹精度评定。假设任务轨迹为S时,必须保证机器人末端执行器位置与方向时刻沿着指定轨迹S,则表示为:
式中:t为时间变量t∈[0,T],当t=0时对应轨迹S上的起点,t=T对应轨迹S上的终点。
指定轨迹为直线时,由于轨迹误差,运动的实际点无法保证在指令轨迹上,因此必定存在实际点与理想轨迹之间有个距离偏差d。当指定轨迹为圆弧曲线时如图所示,轨迹上的红点为机器人轨迹插值点,P1为轨迹上的采样点,P2为指令轨迹的理想点。当t足够小时,相邻轨迹插值点的圆弧段可近似为直线段,当前点到轨迹的距离可近似为到直线段的距离d。点p0(x0,y0,z0),p1(x1,y1,z1)为直线规划的两点,p2(x2,y2,z2)为某时刻机器人运动点,pc(xc,yc,zc)为垂足点。直线方程为
其中(m,n,p)为直线的方向向量,点xc在直线上,故
则xc=mt+x1,yc=nt+y1,zc=pt+z1,垂线向量为(x2-xc,y2-yc,z2-zc);
由垂线向量与直线方向向量垂直得
则可求得:
由t、xc、yc、zc得点到直线的距离为:
设定进行运动N次该轨迹,则可通过指令理想轨迹上的具体点与实际轨迹之间的距离均方根RMS评定机器人轨迹精度。
3 补偿算法及仿真
3.1 机器人轨迹补偿算法
机器人运动轨迹误差参数补偿采用最为普遍的最小二乘算法,最小二乘法为目前最为常用的通过将误差最小化,寻求误差平方和最小与数据的最佳函数匹配的算法,又称为最小平方法,是一种数学优化方法。在机器人轨迹误差辨识当中可以简便求得参数误差数据,并使参数误差导致的实际轨迹与理论轨迹之间误差的平方和最小,引入轨迹精度目标函数以此求解在轨迹精度下的机器人最优几何参数值。
将实际轨迹与理论轨迹在一定参数值下的轨迹误差函数设定为S(δ),将S(δ)=0改写为δ=φ(δ),φ(δ)为迭代函数,理论的几何参数值若为δ0,代入φ(δ)中,则δ1=φ(δ0),得到迭代一次后的结果δ1,返回上述过程得到δ2=φ(δ1),迭代k次后结果为:
得到的序列为δ0,δ1,δ2,…δk,…,若迭代序列{δ}收敛到δ*,则能够使得:
则δ*=φ(δ*),即δ*为函数S(δ)的最优解,若序列{δ}发散则迭代不收敛。
将最小二乘算法应用于机器人轨迹误差参数辨识当中辨识,由机器人轨迹误差模型ΔS=Jδ·δ转换成δ=φ(δ)的形式,当误差系数矩阵Jδ因奇异性无法求逆时,采用轨迹误差参数迭代模型为:由于雅可比矩阵Jδ奇异性问题,则需对轨迹误差影响较大的冗余参数进行去除,即去除冗余参数δi对应的雅可比阵列,从而避免雅可比矩阵Jδ产生奇异值,保证辨识的运动参数与理想值接近,其中δi为冗余参数,i∈(1,24)。
基于轨迹误差参数迭代模型进行运动学参数辨识,在六自由度机器人工作空间选取任意点或指定轨迹上的点进行激光跟踪仪测量,得到各点的实际位置以及机器人的实际轨迹,经坐标系转化后计算轨迹偏差值ΔATk,轨迹误差参数辨识为:
以此得到满足机器人在所需轨迹精度要求运行运动轨迹下的运动参数最优值。
3.2 机器人轨迹补偿仿真
机器人在运动过程中的位移、速度和加速度形成机器人的运动轨迹,运动轨迹的形成可分为关节空间运动轨迹与笛卡尔空间运动轨迹,即直接确定轨迹目标点所对应的机器人的关节角θ或直接给定目标点在机器人坐标系下的空间位置坐标进行轨迹规划。对机器人常用的直线、圆弧轨迹进行轨迹偏差分析,即在机器人连续运动过程中考虑运动学误差因素使得所走点位产生偏差最终引起轨迹的整体偏差ΔS。
在机器人最大工作空间范围内或在指定运动轨迹上选取一定量的测量点,在轨迹精度模型的基础上通过轨迹辨识补偿算法确定在轨迹精度范围内的最优运动学参数值并修正,使得机器人在补偿后的运行轨迹更接近于理论轨迹(如下页图3,图4所示)。
4 实验过程及分析
4.1 机器人轨迹补偿结果验证
通过加工的连接板将靶球安装在机器人末端,放入1号位置靶球,使用激光跟踪仪进行测量。工具坐标系标定示意如图5所示:
在机器人工作空间选取点C1(500,100,625),立方体棱长为200 mm的立方体,在跟踪仪RPM中输入C1与棱长值,由其计算C2~C8,P1~P5的坐标值并记录;可在示教模式下绕工具坐标系的X,Y,Z旋转各3个点,三个圆确定其Z轴方向;沿着X,Y轴方向走直线确定X,Y轴方向,计算靶球与机器人末端的偏距值并记录;在机器人控制软件中建立新工具坐标系Tool,输入偏距值并调用该工具坐标系。
50个点的测量结果表明静态误差源经标定后位置误差由平均误差的16 mm提高到0.4 mm,机器人在标定后的位置运动明显提高,除个别点位误差值较大以外,机器人运动精度在标定后的总体性能保持良好,能够进行下一步的机器人轨迹精度的测量实验(如图6所示)。
选定机器人工作空间里指定轨迹上的理论点,使用激光跟踪仪测得机器人的轨迹上的一系列散点,得到其在测量坐标系下的坐标值;通过最小二乘轨迹辨识算法进行计算可以得到机械臂的最优DH参数值见表1。
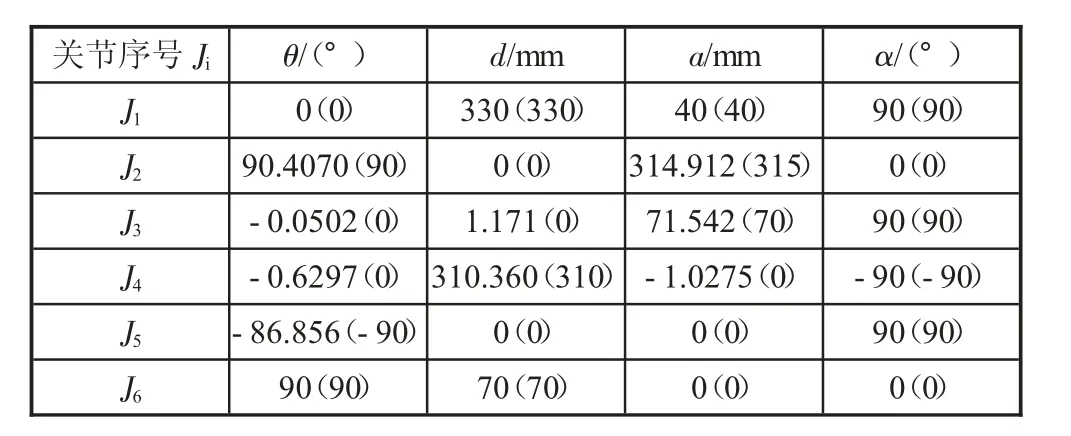
表1 实际与理论运动学参数值
得到在该轨迹精度模型下的最优运动学参数后替代机器人控制器中的理论运动学参数值,进行机器人轨迹精度测量实验,所选轨迹为机器人工作空间最大立方体内的直线与圆弧轨迹,机器人的理论轨迹可由示教器中末端笛卡尔坐标系给出,根据两点确定一条直线,三点确定一圆弧,故可编程使机器人按设定的点位进行轨迹插补,使用激光跟踪仪测量机器人的理论轨迹,设定采样频率为100点/s。首先在机器人最大立方体的对角面上的一条直线与圆弧为例进行误差补偿后的轨迹准确度测量分析(如图7和图8所示)。
SR4C型机器人直线准确度由补偿前的0.414 mm经轨迹静态误差补偿后提高到了0.310 mm,圆弧准确度由补偿前的3.204 mm提高到了2.522 mm,可知经机器人位置误差补偿提高后进行机器人运动轨迹精度仍有一定程度的提高。
4.2 精度评判方法结果验证
按国标上规定进行机器人轨迹补偿前后的实验;即在机器人工作空间最大立方体内任意轨迹上选取一定量测量点进行轨迹误差参数辨识,后使用实际运动学参数值进行机器人轨迹运动测量,通过国家标准中轨迹精度评定方法对其进行轨迹精度评定,得到机器人在该轨迹下的轨迹准确度;对机器人进行轨迹拟合,利用本文提出的轨迹精度评定方法进行评定,得到轨迹准确度值(如图9所示)。
对机器人进行直线轨迹规划运动时,确定机器人最大试验立方体对角面上的直线轨迹,规划点为P2(480,80,655)、P4(320,-80,495),模拟出机器人运动的实际轨迹,运动过程中按采用周期间隔选取点拟合除实际直线轨迹,计算各采样点与直线的距离偏差即拟合度。
在采样的124个点位中,最大偏差点(-668.517,3 213.240,-589.659)的距离误差为0.372 mm,最小偏差点(-468.896,3 102.201,-426.276)距离误差为0.011 mm,与国标的0.391较为接近(如图10所示)。
对机器人进行圆弧轨迹规划运动时,圆弧轨迹规划点为LGC2(456.568 5,0,631.568 5)、LGC3(400,-80,575),LGC4(343.431 5,0,518.431 5)模拟出机器人运动的实际轨迹,运动过程中按采用周期间隔选取点拟合除实际圆弧轨迹,计算各采样点与圆弧的距离偏差即拟合度。
在采样的124个点位中,最大偏差点(-668.517,3 213.240,-589.659)的距离误差为1.27 mm最小偏差点(-468.896,3 102.201,-426.276)距离误差为0.011 mm,与国标的2.731较为接近。
5 结论
本文分析了影响六自由度工业机器人运动轨迹偏差的主要误差源,建立综合轨迹精度误差模型,在对机器人进行预标定的基础上进行基于轨迹精度误差模型的误差参数辨识修正,并对轨迹精度评定方法进行优化和改进,对SR4C型机器人进行轨迹补偿实验及轨迹精度评定的优化方法进行验证,得到以下结论,对机器人在动态误差源影响下的实时补偿修正提供轨迹精度评定的参考依据与理论支持。
1)对机器人运动轨迹误差来源进行分析,得出六自由度工业机器人受到静态误差源与动态误差源,鉴于静态误差源中的主要运动学误差建立较为准确的轨迹精度误差模型经仿真验证了模型的准确性。
2)在进行机器人预标定的基础上进行机器人轨迹补偿精度提高实验,得出直线轨迹准确度比圆弧轨迹准确度更高,直线与圆弧轨迹精度经补偿后都有一定的提高,且提高幅度要比预补偿所提高的幅度低。
3)在机器人试验的最大立方体上进行轨迹精度评定优化方法验证实验,得直线轨迹精度经评定后准确度为0.372与国标评定的0.391相接近,圆弧轨迹精度经评定后准确度为0.408与国标评定的0.391相接近。

