时变交通下社区团购生鲜配送多目标优化
杨习杰,马云峰,2 YANG Xijie,MA Yunfeng,2
(1.武汉科技大学 恒大管理学院,湖北 武汉 430065;2.武汉科技大学 服务科学与工程研究中心,湖北 武汉 430065)
0 引 言
社区团购是一种以生鲜类商品作为切入点,依托于本地社区和团长的个人资源在小范围区域内进行团购的新型电商零售模式。用户当日线上下单,次日在社区团长处自提,由专门的平台提供采购、物流仓储及售后。受疫情影响,自2020年以来,社区团购订单量出现井喷式增长,社区团购市场发展迅猛,随之而来的生鲜配送问题受到诸多学者关注。
社区团购生鲜配送问题可以看作车辆路径问题的一种变体,与传统电商不同,社区团购一般属于小范围配送,并且对于配送的时效性要求更高。目前关于社区团购的研究主要聚焦在其运营模式上,对订单配送展开研究的较少,一般都是基于静态路网,以成本、满意度等为目标,加入了时间窗等约束。然而,社区团购的配送是面向城市道路,在实际配送过程中,必须要考虑到时变交通路网对于车速的影响。近年来,在时变路网的车辆路径问题研究中,常见的优化目标诸如成本、行程时间、碳排放量、车辆使用数量、顾客价值和顾客满意度等。由于该问题属于NP-hard,在模型求解上也以一些元启发式算法为主,包括遗传算法、蚁群算法、粒子群算法、模拟退火和禁忌搜索算法等。赵志学和李夏苗综合考虑了最低新鲜度约束,车载限制和电动车电量约束,利用设计的自适应的蚁群算法求出了最低配送成本。王宁等以客户价值和满意度为优化目标,假设车速在同一时段内保持恒定,考虑了时间窗和车辆载重等约束,利用线性加权法将双目标转化为单目标,并设计了单亲遗传算法进行求解。
本文以配送成本最小和配送时间最短为目标,建立了时变交通下社区团购生鲜配送双目标优化模型,在传统的遗传算法基础上先后引入了进化逆转操作和改进的精英保留策略,用于提高遗传算法的局部寻优能力,最后通过具体算例对模型和算法进行验证。
1 问题描述与模型建立
1.1 问题描述
本文研究的时变交通下社区团购生鲜配送多目标优化问题可以被描述为:以单个配送中心作为配送车辆的起止点,由一组同质车队为多个社区团长点配送货物,考虑时变路网对车辆速度的影响,并以总配送成本最少和总配送时间最短为目标,对车辆的配送路径进行规划。该问题的示意图如图1所示。
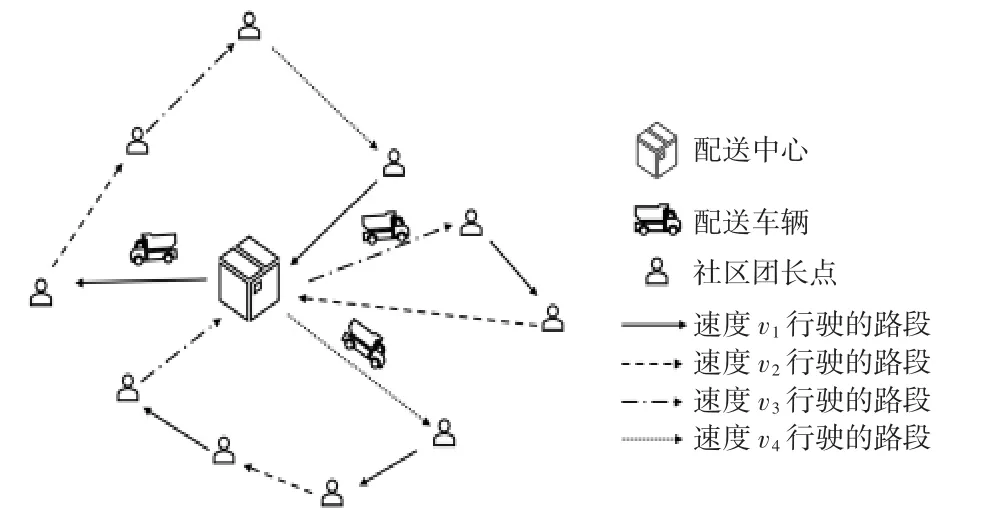
图1 时变交通下社区团购生鲜配送多目标优化模型示意图
针对问题的可操作性,本文做出以下基本假设,使用的符号及参数说明如表1所示。

表1 符号及变量说明
(1)配送中心可以满足所有客户点的需求,车辆从配送中心出发,最终回到配送中心,并且车辆载重不能超过其最大载重量;
(2)每个社区团长点仅由一辆车服务,所有的社区团长点都要被服务,服务时间相同;所有社区团长点的需求量、地理位置等信息已知,所有车辆最早8点从配送中心出发,在16:00前完成所有需求点的配送任务;
(3)假设交通状态对车辆速度的影响是基于时间段的,车辆在每个时间段内的速度保持不变。
1.2 配送成本计算
1.2.1 固定成本与运输成本
本文中的车辆是同质的,固定成本一般只与使用的车辆数量有关,车辆在配送过程中产生的运输成本一般与行驶距离呈正比。因此,固定成本和运输成本的表达式如公式(1)和公式(2)所示。

1.2.2 货损成本
生鲜在配送过程中往往会因为配送时间过长造成物品腐败、变质等,从而形成了货损成本。假设生鲜配送过程中,车内的温度恒定,那么生鲜产品到达社区团长点i处的新鲜度表达式为:

假设货损成本只与生鲜产品的数量、单价以及产品的新鲜度有关,那么货损成本为:

1.3 配送时间的计算
在实际的交通路网中,配送车辆的实际速度与车流量和车速限制有关。道路交通拥堵指数(Traffic Performance Index,TPI)是用来反映道路交通拥挤程度的一种数字化表现,本文按照百度地图道路交通拥堵指数分为畅通、缓行、拥堵和严重拥堵四个等级,畅通(1~1.5)、缓行(1.5~1.8)、拥堵(1.8~2)和严重拥堵(2以上)。本文中的TPI表示为车辆实际行程时间与畅通行程时间的比值,TPI的值越大也代表着道路的拥堵程度越高。因此,车辆的实际速度与车速限制和TPI的关系表示为:

在本文中,假设每天的配送时间被分为p个时间段,车辆从社区团长点i处出发,到社区团长点处完成配送并离开,配送时间由车辆行驶时间和服务时间两部分组成。根据各时间段的交通拥堵指数,设计了配送时间的计算方法,步骤如下:


1.4 模型构建
本文建立总配送成本和配送时间最小的时变交通下社区团购生鲜配送双目标优化模型如下:


约束条件为:

公式(6)和公式(7)分别表示目标函数为总配送成本最小和总配送时间最短,公式(8)表示每个社区团长点有且只有一辆车提供服务,公式(9)、公式(10)表示所有车辆只能从配送中心出发一次,最终并回到配送中心,公式(11)为最低新鲜度约束,公式(12)、公式(13)和公式(14)分别为车辆的载重、里程约束和车辆数量约束,公式(15)、公式(16)为到达社区团长点的时间及软时间窗约束,公式(17)为决策变量。
2 算法设计
2.1 双目标优化的求解思想
本文通过线性加权的方法将双目标转化为单目标进行求解。配送成本与配送时间两个目标函数具有不同量纲和数量级大小,直接进行线性加权得出的结果显然是不合理的,因此首先对两个目标函数进行归一化处理,归一化的方法如公式(18):

其中:C为该目标函数的最小值,C为目标函数的一个极大值。根据本文所建立的模型以及设计的算法只能求出目标函数的极大值,其次单目标的最大值在本文的求解过程中意义不大。线性加权后的单目标函数为:

2.2 遗传算法
2.2.1 编码操作
本文采用整数排列的方式进行编码,染色体的长度等于需求点的数量,染色体的每一段对应着需求点的编号,如{8,10,9,6,1,2,5,4,3,7}就是一个正常的染色体。
2.2.2 选择、交叉与变异操作
选择算子采用轮盘赌的方式,每个个体被选中的概率与其适应度的值有关。适应度的值越大,被选中的概率越大,本文设置适应度函数如公式(20)所示。

交叉操作采用双点交叉算子,交叉操作的步骤如下:
Step1:将父代种群两两分为一组,按照交叉概率对每一组进行交叉操作;
Step2:产生两个客户编号范围内的随机整数a和b,交换两个父代a到b范围内的染色体片段;
Step3:交叉后的染色体中可能存在着重复的片段,对于重复的片段按照交叉片段中的映射关系进行处理。
变异操作的方法是,随机选择染色体的两个基本位,按照变异概率交换其对应片段,如图3(a)所示。
2.2.3 进化逆转操作
加入进化逆转操作的目的是为了提高遗传算法的局部寻优能力,进化体现在仅当逆转后适应度值提高才接受逆转,否则逆转无效。换句话说,进化逆转是为了使得每个个体朝着适应度值高的方向逆转。进化逆转操作的步骤如下:

图2 交叉操作示例
Step1:产生两个客户编号范围内的随机整数a和b,将父代a到b范围内的染色体片段按照相反顺序排列后插入至原位置,如图3(b)所示;

图3 变异操作与进化逆转操作示例
Step2:计算逆转后的个体适应度,若适应度值提高,则保留逆转操作,否则逆转无效。
2.2.4 改进的精英保留策略
本文采用改进的精英保留策略主要有以下三点原因:(1)保证子代种群中的最优个体永远不会比父代的差;(2)同时也防止父代中适应度高的个体由于交叉、变异等操作而丢失;(3)增加随机保留策略,在一定程度上避免了算法陷入局部最优。精英保留策略的具体操作步骤如下:
Step1:计算父代中个体适应度值的集合Fit,计算经过选择、交叉、变异和进化逆转等操作后的个体适应度值的集合Fit;
Step2:将Fit和Fit放在一起,按照适应度值由高到低排序,根据精英保留比例先选出一定比例的子代个体,将这部分个体替代Fit种群中适应度值较差的个体,从而形成新的子代种群进入下一步迭代。
3 数值实验
3.1 实验设计
本文中的部分数据来源于文献[5],包括各社区团长点的位置坐标、需求量和距离等数据,其中各节点间的距离是通过高德地图得到的实际最小距离。各时间段的交通拥堵指数及其他相关参数如表2和表3所示。

表2 各时间段的交通拥堵指数
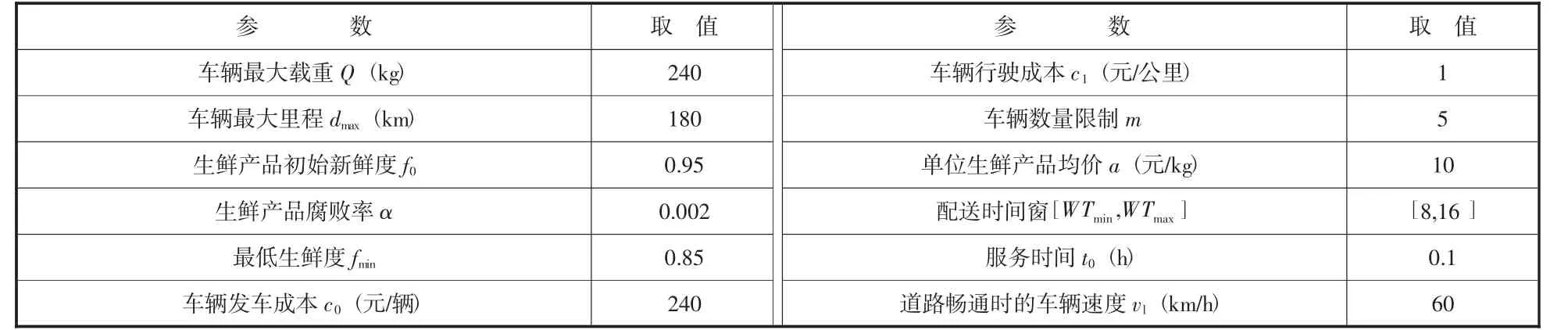
表3 其他相关参数
车辆从配送中心的出发时间为8:00,改进遗传算法的初始种群规模为150,迭代次数为1 000,交叉概率为0.9,变异概率为0.1,精英保留比例为0.3,算法采用MATLAB 2018a软件编写。
3.2 算例求解
采用简单的遗传算法、加入进化逆转算子的遗传算法和本文中改进的遗传算法分别求解单目标下的配送成本最小值,每种算法下均进行20次计算,取20次中的最优值作为配送成本的最小值,三种算法的优化过程如图4所示。由图4可以看出,改进的遗传算法相比于另外两种算法具有更快的收敛速度,同时也更不容易陷入局部最优。

图4 改进遗传算法的配送成本迭代过程
根据上述所给参数计算单目标下的极大值和最小值,总配送成本和配送时间的极大值与最小值分别为:2 460.65元、18.9558小时、1 447.62元、7.9235小时。
将上述结果代入公式(18)和公式(19),λ取值集合为0.1到0.9,步长为0.1,不同λ取值下的仿真结果如表4所示。
表4中所求出的解均可以作为双目标优化的帕累托最优解,当λ取值在0.2到0.7时,求得的双目标优化的解是相同的,因此本文取配送成本为1 457.01元,配送时间为7.9576小时作为最终的解,对应的配送路径的可视化如图5所示。

表4 不同λ取值下的仿真结果

图5 双目标优化下的具体配送路径
为了进一步分析交通状况的变化对生鲜配送过程的影响,λ取0.5,在其他条件不变的情况下,设置不同的车辆出发时间,利用改进的遗传算法进行求解,仿真结果如表5所示。
由表5可以看出,车辆的出发时间主要对货损成本和总配送时间的影响较大,主要原因在于,当配送时间段内的道路交通拥堵指数较低时,车辆以更高的车速完成配送,各个客户也能更早地收到货物,从而降低了货损成本、缩短了配送时间。

表5 不同车辆出发时间下的仿真结果
4 结论
本文在综合考虑生鲜最低新鲜度、软时间窗和车载限制等约束的情况下,建立了以总配送成本最小和配送时间最短为目标的时变交通下社区团购生鲜配送双目标优化模型。采用分段求解的方法计算时变路网下车辆行驶时间,通过极大极小归一化和线性加权处理,将双目标转化为单目标,并设计了改进的遗传算法进行求解。实验结果表明,社区团购企业在生鲜配送调度过程中,要充分考虑到交通状况对生鲜配送的影响,合理规划配送路线,在可能的情况下,尽量避免拥堵时段,从而达到降低配送成本、缩短配送时间和提高客户满意度的目的。

