共轴双旋翼无人机设计与实现
王棒 苏成悦 徐胜 陈元电 施振华


摘要:文章首先通过SolidWorks设计一种矢量共轴双旋翼无人机,其主要由共轴式电机和两个舵机组合而成,共轴式电机提供升力、利用上下旋翼的差速产生反扭矩控制偏航,舵机控制升力方向实现翻滚和俯仰。为研究如何控制其飞行,文章接着设计一款专用的飞行器控制系统。硬件方面,主控采用STM32F4,姿态传感器采用mpu9250九轴传感器,气压传感器采用BMP280。软件方面,实时操作系统采用FreeRTOS嵌入式,姿态解算采用Mahoney互补滤波算法,姿态控制算法采用串级PID。姿态控制量和油门值融合得到总控制量,总控制量转化为4路PWM信号分别控制两个电机和两个舵机。
关键词:FreeRTOS实时操作系统;共轴双旋翼;Mahoney互补滤波;串级PID
中图分类号:TP311 文献标识码:A
文章编号:1009-3044(2022)13-0001-04
随着科技的发展,无人机逐渐进入人们的视野,各种气动布局的无人机层出不穷。共轴双旋翼无人机具有除和常规旋翼无人机垂直起降的功能外,其还具有结构紧凑、重量小、便携性高、效率高、续航久等功能特点[1]。因此,常规多旋翼能胜任的航拍、测绘、救援等任务,共轴双旋翼无人机也可以胜任。但由于其本身的结构和气动布局的特殊性,飞行时易受到外界因素的干扰。所以控制其稳定飞行、提高响应速度也成为必须,共轴双旋翼无人机整体结构如图1所示。
1飞行器结构与控制原理
如图2所示,共轴双旋翼飞行器动力与方向控制部分包含一对8040桨叶、一个1400KV 2204共轴电机、两个20A电调、两个金属数字舵机。①②③④分别为翻滚舵机、俯仰舵机、顺时针电机、逆时针电机。
共轴双旋翼在空中悬停后,可进行八种运动。如垂直升降运动时,顺逆电机同时加速或减速,俯仰和翻滚舵机保持水平;俯仰和翻滚运动时,保持机身稳定不掉高情况下,舵机发生对应的倾转,使升力与重力的合力方向为俯仰或翻滚方向;偏航运动,利用上下电机的转速差产生的反扭矩实现。如顺时针偏航时,逆时针电机加速(其产生顺时针的扭矩增大),顺时针电机减速(其产生逆时针的扭矩减小),产生使机身顺时针旋转的总扭矩。各种姿态运动时,顺逆电机和俯仰翻滚舵机的状态如表1所示。
1.1飞行控制系统总体框图
整个飞行控制系统主要包括三个部分[2]:上位机系统、遥控系統、飞行控制器。飞行控制器通过USB数据线连接上位机系统,在上位机界面调整飞行控制器的PID参数、校准遥控器各通道量程、校准加速度计陀螺仪等。遥控系统采用支持SBUS协议且工作频段为2.4GHZ的航模遥控器和接收机。飞行控制器依据遥控器传入的数据,控制共轴双旋翼无人机的姿态,同时将电量等信息回传给遥控器,具体过程如图3所示。
2系统硬件设计
2.1飞控系统硬件设计
文章选择了STM32F405RGT6作为飞行控制器的主控,上电自动复位,启动模式可通过BOOT0引脚的按键选择。采用MPU9250检测姿态[3],BMP280气压计测量高度。支持SBUS和PPM两种无线通信协议,分别采用两路12位ADC检测电源的电压和电流,当电量不足时触发蜂鸣器报警。通过三色指示灯3528RGB指示飞行控制器的状态,采用TF卡记录飞行数据。采用SWD协议下载和调试代码,采用3个定时器产生6路不同频率的PWM作为控制信号,如图4所示。
2.2数据传输
接收机与飞行控制器可采用SBUS或者PPM通信,可以通过焊盘的焊接选择。SBUS总线是一根串行总线,通过这根线即可获取遥控器各通道的数据,SBUS总线协议使用的是TTL电平的反向电平,可利用三极管的开关特性实现。接收机的输出端连接SBUS_IN,其为高电平时,NPN三极管导通,此时输入端SBUS电平为低电平信号。反之若SBUS_IN为低电平时,三极管不导通,SBUS为高电平。SBUS引脚连接的是主控芯片的串口RX引脚,利用外设串口6实现数据接收,如图5所示。
2.3控制信号输出
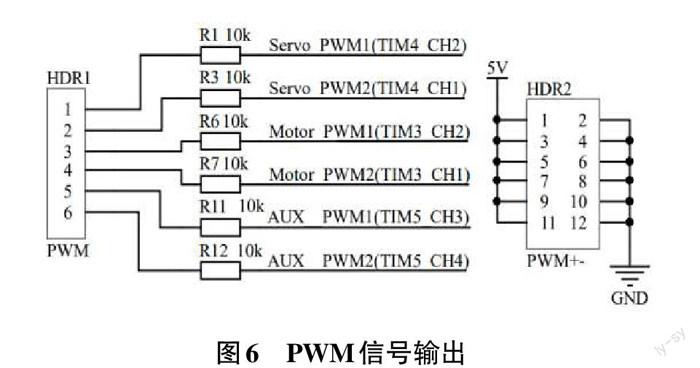
输入给无刷电调的PWM频率,不会影响电机的转速,但会影响控制频率和精度,飞控输出给电调的PWM传递的是1ms~2ms脉宽的信号,脉宽越宽,转速越快。电调会根据这个脉宽来驱动电机。为了满足对共轴电机控制频率和精度的需求,使用定时器3的两个通道产生频率为400Hz的PWM信号分别输入给两电调;因同一个定时器各通道的PWM频率一样,故舵机采用定时器4的两个通道产生脉宽为0.5ms~2.5ms、周期为20ms的PWM信号分别输入给舵机,对应舵机转动角度为0°~180°[4]。另外,利用定时器5设计了两路辅助PWM用于驱动挂载设备,如图6所示。
3系统软件设计
3.1 FreeRTOS任务调度
主要任务之间的调度如图7所示。
UsbRxTask任务负责将上位机通过串口发送过来,存在UsbData队列的数据,打包成ATKP格式数据包,再存入RxQueue队列。
RxAnlTask任务负责将RxQueue队列的ATKP格式包解析,将上位机或者遥控器发来的控制指令发送给StabTask任务。
StabTask任务负责将传感器数据融合,得出姿态,再根据获取的控制数据,进行PID控制和动力分配,控制电机和舵机使机身保持平稳。
TxTask任务负责将StabTask任务的姿态数据、电机和舵机PWM输出数据等打包存入TxQueue_R和TxQueue_U队列,再分别由RadioTask发送给遥控器,UsbTxTask发送给上位机。
3.2 Mahoney互补滤波数据融合算法
MPU9250自带的数字运动处理器DMP不需要主控参与运算还能直接输出四元数,但由于DMP最短采集数据周期为5ms,故采用直接读取数据的方法。在数据融合前,先对加速度计数据IIR滤波,对陀螺仪数据加偏置调整,再通过Mahoney互补滤波融合数据[5]。
3.2.1 旋转矩阵
设有两个坐标系分别为地理坐标系[E]和机体坐标系[B0],起初机体坐标系[B0]和地理坐标系[E]重合。令机头方向为X轴的正方向,将X轴称为翻滚轴,Y轴称为俯仰轴,Z轴称为偏航轴。當机体坐标系绕着Z轴旋转一定角度y,得到新的机体坐标系[B1],此时机[B1]已经不和地理坐标系重合。再绕[B1]坐标系中的Y轴旋转一定角度得到新的坐标系[B2]。最后绕[B2]坐标系的X轴旋转一定角度r,得到最后的机体坐标[B]。即旋转顺序为Z—>X—>Y。绕各轴旋转时,旋转方向为右手方向,每次转动对应一个基本旋转矩阵如下:
[CB1E=cosysiny0-sinycosy0001(绕Z轴)CB2B1=cosp0-sinp010sinp0cosp(绕Y轴) CBB2=1000cosrsinr0-sinrcosr(绕X轴)]
由地理坐标系[E]至最终的机体坐标系[B]的姿态变换矩阵如下:
[CBE=CBB2CB2B1CB1E=cospcosycospsiny-sinpcosysinpsinr-cosrsinycosrcosy+sinpsinrsinycospsinrsinrsiny+cosrcosysinpcosrsinpsiny-cosysinrcospcosr]
3.2.2 四元数与姿态变换矩阵
当刚体定点转动,只考虑[E]系相对[B]系的角位置时,可当作[B]系是由[E]系没有经过中间过程,而是一次性等效旋转形成的[6],得到[B]系至[E]系的姿态变换矩阵:
[CEB=q02+q12-q22-q322q1q2-q0q32q1q3+q0q22q1q2+q0q3q02-q12+q22-q322q2q3-q0q12q1q3-q0q22q2q3+q0q1q02-q12-q22+q32]
[CEB]与[E]系至[B]系的姿态变换矩阵[CBE]互为转置的关系:
[CBE=CEBT=q02+q12-q22-q322q1q2+q0q32q1q3-q0q22q1q2-q0q3q02-q12+q22-q322q2q3+q0q12q1q3+q0q22q2q3-q0q1q02-q12-q22+q32]
对比两式:
[-sinp=2(q1q3-q0q2)cospsinycospcosy=tany=2(q1q2+q0q3)q02+q12-q22-q32cospsinrcospcosr=tanr=2(q2q3+q0q1)q02-q12-q22+q32]
得到四元数转欧拉角公式:
[p=arcsin2(q1q3-q0q2)y=arctan2(q1q2+q0q3)q02+q12-q22-q32r=arctan2(q2q3+q0q1)q02-q12-q22+q32]
加速度计测量到的加速度数据是基于机体坐标系的,而重力加速度向量[Ge]=[00gT]是地理坐标系的,两者要在同一个坐标系下做叉积运算。如图8所示,把[Ge]转到机体坐标系,得到其在机体坐标系表示的向量[Gb]。
根据上一采样周期得到的姿态矩阵[CBE]左乘[Ge],可以得到理论上在机体坐标系下表示的重力加速度[Gb],根据矩阵乘法,[Gb]也就是地理至机体坐标系姿态变换矩阵[CBE]的第三列:
[Gb=CBEGe=2q1q3-q0q22q2q3+q0q1q02-q12-q22+q32=g1g2g3]
则有:
[ρ=Ab×Gb=ijka1a2a3g1g2g3=0-a3a2a30-a1-a2a10g1g2g3ijk]
其中,[Gb]为单位理论加速,[Ab]为传感器测量的单位加速,所以[Gb=1]和[Ab=1],推出:
[ρ=AbGbsinθ=sinθ]
当[θ]很小时,[sinθ≈θ],即[ρ≈θ=error]。
[error=exeyez=0-a3a2a30-a1-a2a10g1g2g3=a2g3-a3g2a3g1-a1g3a1g2-a2g1]
[ρ]向量大小可以看作是[Ab]与[Gb]两向量的夹角。夹角大,说明理论上的加速度和测量得到的加速度偏差大。这是由于陀螺仪的积分误差使旋转矩阵不准确,造成理论加速度不够真实。陀螺仪数据虽不完全准确,但是也不能因此完全信任加速度测得的数据,为了减小这种偏差,使两向量尽可能重合,需二者数据合理采纳。因此采用比例积分PI器控制补偿误差的大小与精度,得到补偿量[error_GYRO]:
[error_GYRO=Kp?error+Ki?error]
其中,比例项用来控制传感器的“可信度”,[Kp]大则偏向加速度计,小则偏向陀螺仪,积分项用来消除静态误差,把补偿量加到角速度上,得到可信度较高的陀螺仪数据。
[Value_GYRO=Value_GYRO+error_GYRO]
最后,代入一阶龙格库塔(Runge—Kutta)算法[7-8],更新得到能代表当前姿态的四元数,其中[wxwywz]就是修正后的角速度,[t+Δt]表示下一时刻。
[q0q1q2q3t+Δt=q0q1q2q3t+12?Δt-wxq1-wyq2-wzq3wxq0-wyq3+wzq2wxq3+wyq0-wzq1-wxq2+wyq1+wzq0]
再将更新后的四元数代入四元数转欧拉角公式,得出最新姿态角,再利用串级PID控制姿态。
3.3 PID控制算法
对模拟PID离散化后的PID算法数学表达式如下:
[U(n)=Kp×e(n)+Ki×i=0ne(i)+Kd×(e(n)-e(n-1))]
式中:[Kp]为比例系数,[Ki]为积分系数,[Kd]为微分系数,[e(n)]=期望角度-实际角度
算法流程图如图9所示,定高模式采用的是单级PID,遥控器油门值转换为Z轴速度值,高度估计值来自Z轴加速度值和气压计BMP280测量的高度值的数据融合,高度期望值为Z轴速度值的积分,偏差值为高度期望值与高度估计值之差,经过单级PID作用后输出油门控制量。手动模式下遥控器油门值为油门控制量。姿态控制采用串级PID,角速度环作为内环,角度环作为外环,即P-PID[9-10]。外环的输入为期望角度与测量角度之差,输出作为期望角速度,其与测量的角速度之差作为内环输入,内环的輸出即为姿态控制量。
4 实验与结论
文章通过STM32单片机和MPU9250姿态传感器芯片设计了一款共轴双旋翼飞控。通过Mahoney互补滤波算法,将陀螺仪和加速度计的数据融合,得到姿态角。再采用串级PID(角度环+角速度环)得到姿态控制量,将姿态控制量和油门控制量整合后,产生对应的PWM信号控制电机和舵机。实物飞行如图10所示,因未融合磁力计数据,飞行一段时间后会偏航,还略有掉高现象,但总体飞行效果达到预期。后续可以采用串级PID(位置环+速度环)作为定高方式。
参考文献:
[1] 陈铭.共轴双旋翼直升机的技术特点及发展[J].航空制造技术,2009,52(17):26-31.
[2] 陈旺才,陈虢,徐君,等.基于STM32的四旋翼飞行器姿态控制器设计与实现[J].电子测量技术,2020,43(19):165-168.
[3] 赵嵌嵌.一种基于MPU9250的四旋翼姿态解算改进算法[J].机械工程师,2019(5):36-39.
[4] 单树清.基于STM32的无刷直流电机控制系统研究[D].兰州:兰州交通大学,2021.
[5] 徐恩松,陆文华,刘云飞,等.基于Mahony滤波算法的姿态解算与应用研究[J].智能计算机与应用,2019,9(5):80-83.
[6] 梅春波.捷联惯性导航系统惯性系非线性初始对准技术研究[D].西安:西北工业大学,2016.
[7] Shi T N,Lu N,Zhang Q,et al.Brushless DC motor sliding mode control with Kalman Filter[C]//2008 IEEE International Conference on Industrial Technology.April 21-24,2008,Chengdu.IEEE,2008:1-6.
[8] 黄权,李立欣,高昂,等.基于Runge-Kutta法的小型无人机姿态角算法研究[J].电子设计工程,2017,25(11):133-136.
[9] 吴东旭,丁茹,张梓嵩,等.基于P-PID控制器对共轴双旋翼飞行器的姿态控制[J].沈阳理工大学学报,2019,38(4):58-61.
[10] 冯庆端,裴海龙.串级PID控制在无人机姿态控制的应用[J].微计算机信息,2009,25(22):9-10,45.
【通联编辑:梁书】

