基于虚警可控梯度提升树的海面小目标检测

刘安邦 施赛楠 杨静 曹鼎

0 引言

海面小目标(浮冰、小船、蛙人、飞机残骸等)已成为海洋雷达探测的主要对象[1-3],海面小目标探测在海上救援、海洋防卫、海上突击等方面具有重要意义．通常,海面小目标的回波较弱,往往被淹没在强海杂波背景下．由于小目标的信杂比(Signal-to-Clutter Ratio,SCR)低,传统的检测器会出现检测概率低、虚警点多等问题．

在雷达信号处理中,长时累积技术是提升小目标SCR的有效途径．在秒级长时观测下,海杂波具有复杂的空时变特性[4-5]．同时,小目标的功率不再保持恒定,具有起伏特性．从海杂波幅度非线性建模出发,Hu等[6]提出了基于Hurst指数的检测器,利用海杂波和目标回波在多尺度分形特性上的差异性,实现了单特征检测．通过对时域数据进行经验模态分解、重构和去噪等预处理,张林等[7]提出了基于变换域分形特性的检测器．从多特征联合角度出发,Shui等[8]提出了基于三特征的检测器,联合一个时域幅度特征和两个频域多普勒几何特征,在三维特征空间中,该检测器采用快速凸包学习算法,获得虚警可控的判决区域．而Shi等[9]提出了基于时频三特征的检测器,充分挖掘了目标和海杂波在时频域的精细化几何特征,包括频谱的波动性和分散性．考虑不同特征对不同数据的敏感性,联合使用更多互补特征成为进一步提高检测性能的有效途径．

在高维特征空间中,目标检测的主要难点是设计虚警可控的分类器．目前,主要有两条途径可以实现高维分类器设计．第一条途径是特征压缩,将高维分类器简化为低维分类器．通过沿着一类最大方差方向投影到低维空间中,Gu[10]提出了基于主成分分析(Principle Component Analysis,PCA)的三特征检测器．基于两类最大距离的压缩,Shui等[11]提出了基于B氏距离的特征压缩检测器．但是,特征压缩势必会带来部分性能损失．第二条途径是设计高维分类器．郭子薰等[12]提出了改进的KNN算法,实现高维判决区域划分．通过调节参数实现虚警控制,Zhou等[13]提出了基于决策树的特征检测器．这些检测器保证了高维信息量,但高维分类器需要遍历搜索参数以满足给定虚警率,导致计算量大且控制不准确．因此,亟需设计虚警可控且计算复杂度低的高维分类器．

为了满足实际雷达快速检测的需求,本文引入梯度提升树(Gradient Boosting Decision Tree,GBDT)[14-15]算法,快速获得高维域虚警可控的二分类器．GBDT分类器集成了多个弱分类器,具有显著的泛化性能以及更高的分类准确度．首先,将从时域、频域、时频域提取的多维特征作为GBDT分类器的输入,获得属于一类的概率预测值．然后,将之作为检测统计量,获得虚警可控的判决门限．最后,基于实测数据的实验结果表明:所提出的检测器能快速获得判决门限,实现海面小目标检测性能提升的目标．

1 高维特征域二分类目标检测

1.1 二元假设检验

假设雷达接收到某个距离单元的N个连续脉冲,构成观测向量z=[z(1),z(2),…,z(N)]T．若观测向量只包含杂波,则称H0假设;若观测向量由目标回波和杂波组成,则称H1假设．因此,传统的雷达目标检测问题归结为二元假设检验:

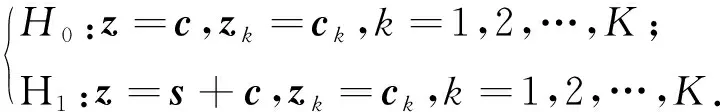
(1)

其中:z和zk分别表示待检测距离单元(Cell Under Test,CUT)以及周围K个参考距离单元的回波向量,为CUT提供杂波信息;c表示海杂波;s表示目标回波;ck表示第k个距离单元为海杂波．

事实上,检测的本质就是判断观测向量属于哪种假设．通常,传统的检测方法基于单个域特性设计统计量,存在小目标检测概率低、虚警点高的问题．基于多特征联合的检测方法主要是利用海杂波和含目标回波在多个域的差异性,并将这些差异性转变为特征,实现高维特征域目标检测．

1.2 高维特征检测问题

为了充分利用观测向量的信息,本文从时域、频域、时频域3个域提取7个特征,分别记为δ1,δ2,…,δ7,如表1所示．在时域,提取Hurst指数[6]和相对平均幅度[8],分别反映幅度的几何粗糙度和能量特性．在频域,提取相对多普勒峰高[8]和相对向量熵[8],分别反映海杂波和含目标回波在频谱宽度、聚集度方面的差异性．在时频域,提取脊能量[9]、连通区域数目[9]和最大连通区域尺寸[9],进一步精细化动态频谱的几何特性．此外,表1给出了2种假设在不同特征下相对取值的大小,这与海杂波和含目标回波的差异性有关．

表1 7个特征描述

考虑到不同特征的取值范围不同,对每个特征作归一化预处理,保证所有特征投影到相同的尺度上．对于第i个特征,假设获得H0假设下Q个样本,归一化定义为

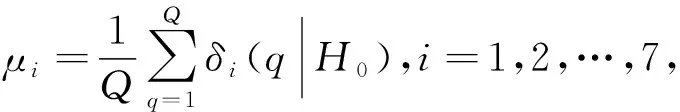
(2)

其中,μi表示第i个特征的均值．

下面,构建高维特征空间．为了保证信息的充分运用,将每个特征作为一个维度,构建七维特征空间．此时,观测向量转换为归一化特征向量为

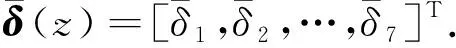
(3)

在高维特征空间中,式(1)中的目标检测问题转化为二分类检测问题,即:

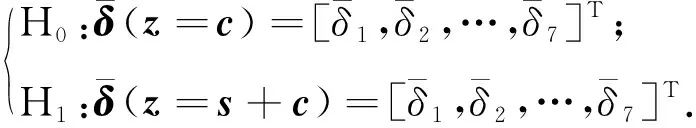
(4)

第一类为H0假设,观测向量只含杂波;第二类为H1假设,观测向量含有目标回波．因此,高维特征域中分类问题的核心在于设计一个具有虚警可控的二分类器．

2 基于虚警可控GBDT的检测器

2.1 检测器结构

基于虚警可控GBDT(False-Alarm-Controllable GBDT,FAC-GBDT)检测器的流程如图1所示．整个检测结构包括在线检测分支和离线训练分支两部分．在检测分支,首先,CUT的观测向量通过时域、频域、时频域提取多个特征,并归一化预处理,去除不同尺度的影响；其次,构建高维特征向量,作为GBDT分类器的输入；然后,将GBDT分类器输出的概率预测值,作为统计量;最后,统计量和门限进行比较,获得最终的判决结果．

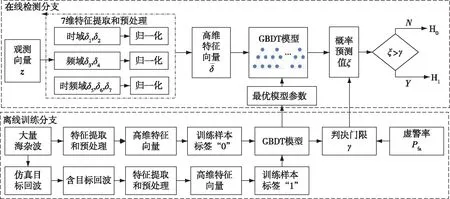
图1 FAC-GBDT检测器的流程Fig.1 Flowchart of FAC-GBDT detector

在训练分支,两类均衡训练样本用于训练学习,获得GBDT模型的最优参数和给定虚警率下的判决门限．通常,由于小目标的空间稀疏性以及军事保密性,海杂波数据可大量获得但含目标回波数据极其稀少．为了提升二分类器的分类准确度,两类的训练样本数目应当均衡．因此,在H1假设下,观测回波建模[10,12]为

z(n|H1)=c(n)+ρ(n)10RSC/20×

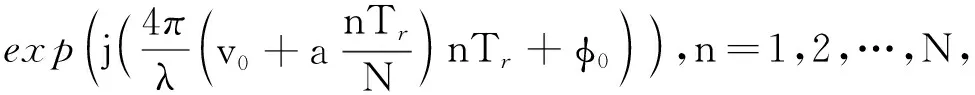
(5)

其中:c是实测海杂波,来自H0假设下的训练数据;ρ是均值为1的相关序列,描述目标起伏特性;RSC为信杂比(SCR)的值;λ是雷达波长;Tr是雷达的脉冲重复周期;|a|≤2是目标的加速度;φ0∈[-π,π]是初始相位;|v0|≤5是目标的初始速度．

在实际工作中,海洋雷达更关注的是在线检测时间．由于GBDT模型参数可离线训练获得,因而不影响雷达实时检测．此外,当探测环境发生变化时,可启动离线训练分支．通过收集当前海杂波数据,重新学习模型的最优参数．FAC-GBDT检测器具有的这种动态更新模式,可以实现对海洋环境的恒虚警特性．

2.2 虚警可控的GBDT分类器

在高维特征空间中,K近邻、决策树、支持向量机等机器学习方法都可以实现二分类．但是,上述分类器自身无法控制虚警率,只能通过建立某个参数和虚警率的关系,进行全局搜索获得给定虚警率下的参数值[12-13]．这类方法明显计算量大,且参数精度设置对虚警精准度有较大的影响．因此,本文引入GBDT算法,无需搜索参数且能精准控制虚警率．

图2给出了GBDT模型的结构[14-15],以Cart回归树作为基本的弱分类器,通过多个弱分类器级联,获得鲁棒性更高的分类结果．GBDT算法核心是一种贪婪最优策略,通过不断减小训练过程产生的残差来达到准确分类．在训练弱分类器的过程中,准则是最小化损失函数．这里,定义损失函数为

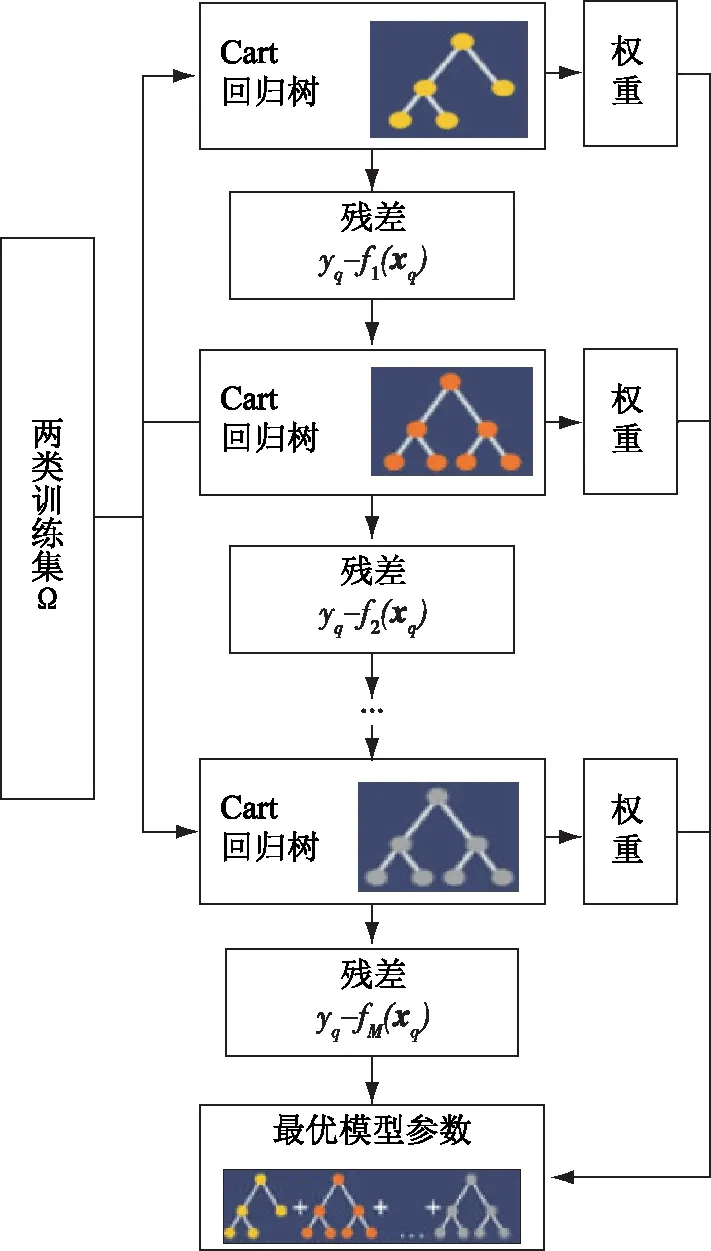
图2 GBDT模型结构Fig.2 GBDT model structure

L(y,f(x))=ylog(1+e-f(x))+

(1-y)(f(x)+log(1+e-f(x)),

(6)

其中,y∈{0,1}表示x的真实标签值,f(x)是y的预测值．

在GBDT分类器训练时,假设H0假设下有Q个向量样本,标签为0;H1假设下有Q个向量样本,标签为1．因此,在7D特征空间中,输入训练集Ω为

Ω={(x1,y1),(x2,y2),…,(x2Q,y2Q)},

xq∈R7,yq∈{0,1}．

(7)

下面,给出GBDT算法的具体步骤．

步骤1.初始化.根据训练集Ω,初始预测值为

(8)

步骤2.生成第m棵Cart回归树.首先,对于第q个样本,计算损失函数的负梯度,即残差值

(9)

然后,通过拟合残差值gm,q,得到第m棵树的叶子节点区域为Rm,j,j=1,2,…,Jm,其中,Jm是第m棵树叶子节点的个数．通过最小化损失函数,计算第j个叶子节点的最佳拟合值cm,j：

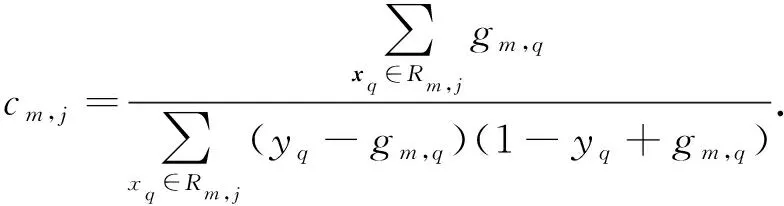
(10)

最后,更新预测值为

(11)

其中,ν∈[0,1]是学习率,用于控制过拟合度．

步骤3.更新迭代.重复步骤2,最终生成M棵Cart回归树．第M棵树的输出,即最终的预测值为

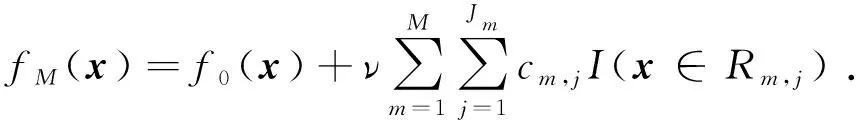
(12)

至此,可以获得GBDT的最优模型参数．

为了获得虚警可控的二分类器,将输入x预测为正样本的概率

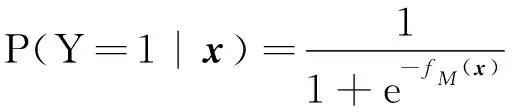
(13)

作为统计量ξ．借助蒙特卡罗实验方法[8-13],将H0假设下Q个样本带入具有最优模型参数的GBDT分类器中,按照式(13)计算获得Q个统计量,记为ξ1,ξ2,…,ξQ．并且,这些统计量按照值从大到小进行排序．那么,在给定虚警率Pfa下,判决门限为

γ=ξ[Q×Pfa],

(14)

其中,[]表示取整数．

图3演示了虚警可控门限的获取过程,设置Pfa=10-3,则11 231个海杂波样本中存在11个虚警点．但是,传统分类器输出以γ=0.5为分界线(即黑色线),存在39个虚警点,虚警率为0.003．这就意味着门限γ=0.5无法保证分类器获得设定的虚警率．因此,调整门限位置至红色直线位置,精确保证虚警点个数为11个．因此,通过调整判决门限,达到设定的虚警率,即虚警可控,实现检测器的恒虚警特性．

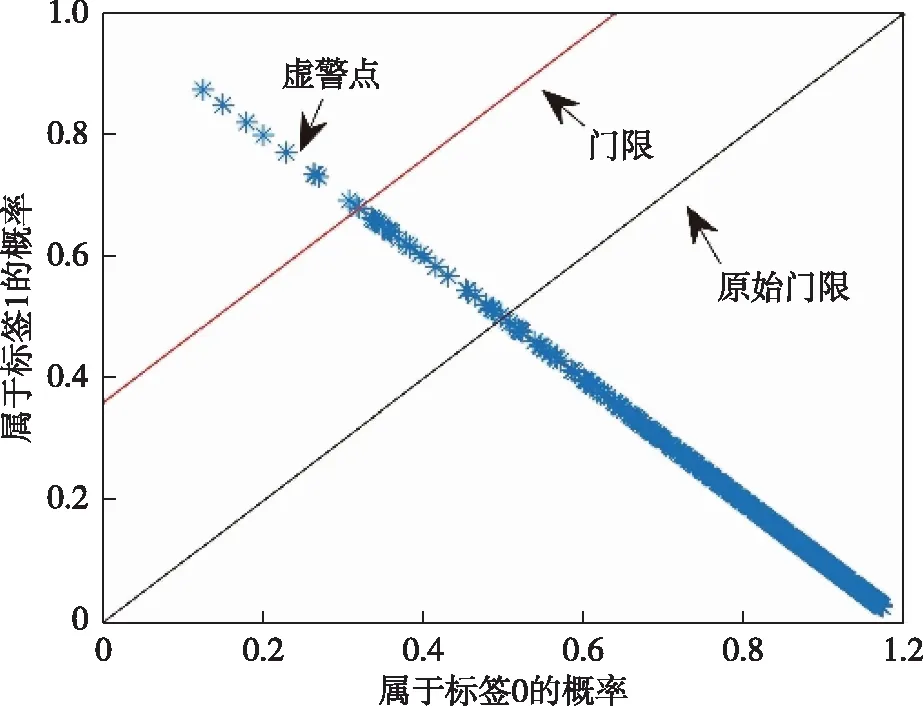
图3 虚警可控判决门限的演示Fig.3 Demonstration of false-alarm-controllable decision threshold

3 实验结果与性能分析

实测数据来自1993年采集的IPIX雷达目标数据库(http:∥soma.mcmaster.ca∥ipix.php.2012.10.11),该数据库是目前公认的小目标测试数据库．实验采用10组数据,每组数据包含14个距离单元、217个脉冲数．雷达工作频率为9.3 GHz,工作在驻留模式,脉冲重复频率fr=1 000 Hz,距离分辨率30 m．测试目标为被金属丝包裹的小球,直径为1 m,可视为漂浮低速运动小目标．每组数据涉及多种海洋环境且SCR起伏较大,具体参照文献[8-10]．

3.1 GBDT分类器性能分析

在高维特征空间中,GBDT分类器的性能影响着后续的检测结果．因此,有必要对分类器性能进行分析．图4演示了二维特征空间中GBDT分类器的区域划分过程．对比第1棵Cart回归树和第15棵Cart回归树的结果,判决区域明显具有较好的划分．随着Cart回归树的增加,判决区域不断地在优化和更新,验证了集成多个弱分类器的性能优势．此外,总的判决区域为非线性边界,适用于非线性的两类样本分类情况．

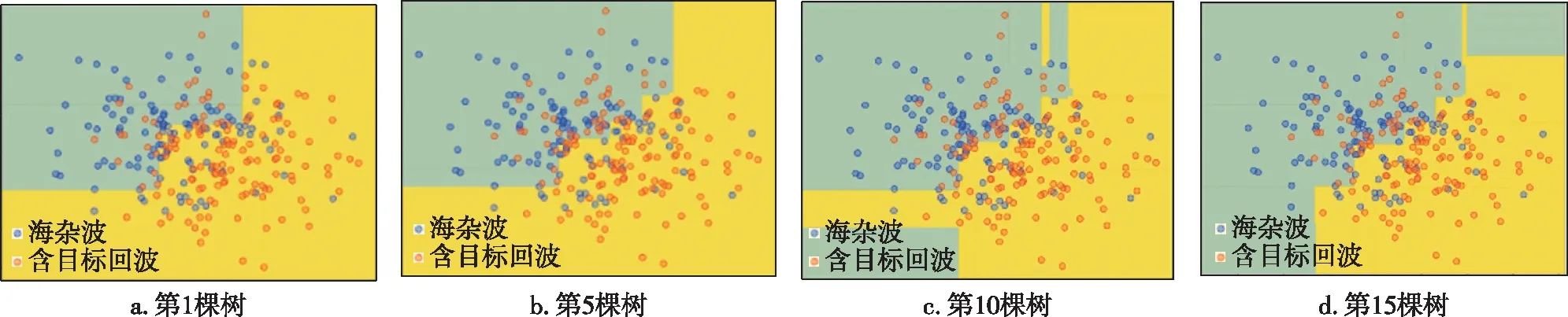
图4 GBDT二分类区域划分过程Fig.4 Division process of dichotomy region in GBDT

图5讨论了Cart回归树数目M和回归树的最大深度D对检测概率的影响．在图5a中,随着M的增大,检测概率上升,这体现了弱检测器集成的优势．但是,这种性能优势在M>12以后,检测概率趋于稳定．在图5b中,当回归树的深度D<5时,检测性能波动性大．因此,综合考虑计算量和性能,设置参数M=15,D=7．

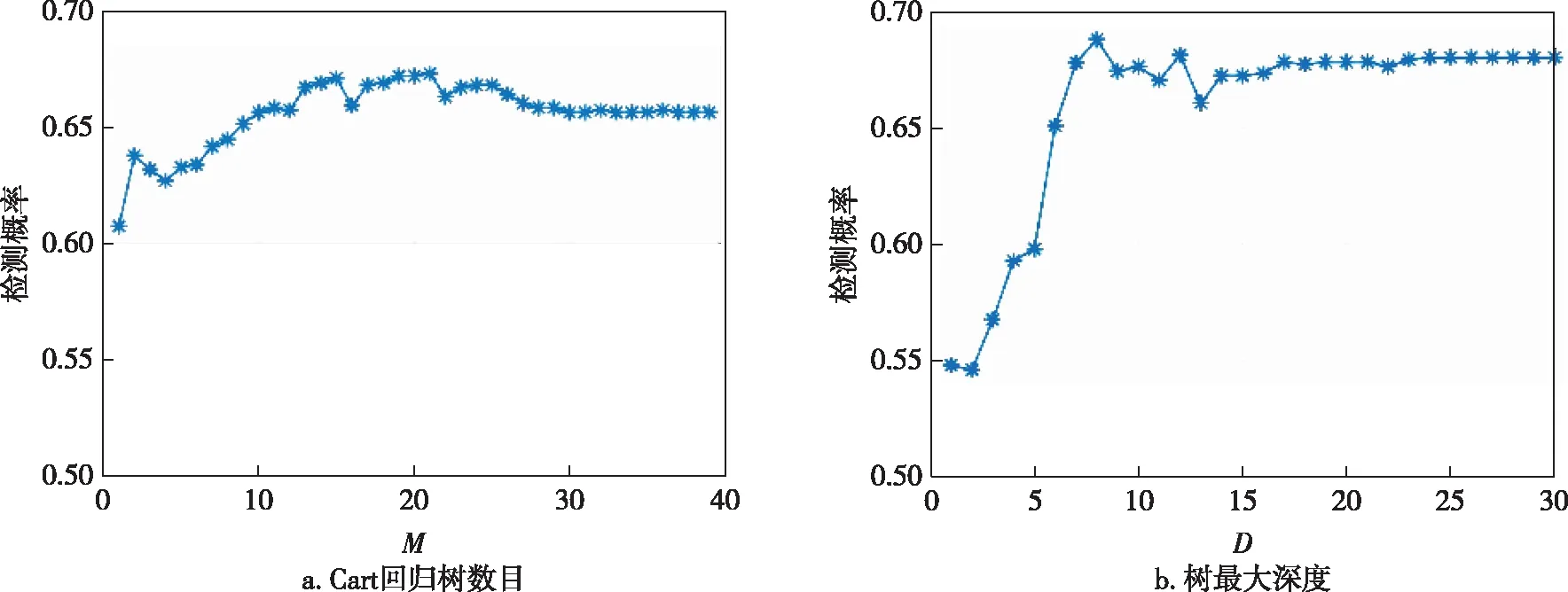
图5 Cart回归树参数对检测性能的影响Fig.5 Parameter influence of Cart regression tree on detection performance

3.2 检测性能对比

实验中,设定Pfa=10-3,脉冲累积数N=512(即观测时间0.512 s)．由于10组数据都含有目标,因而对每组不同极化下数据进行独立检测．在训练分支中,从纯杂波单元和按式(5)产生的含目标回波中,获取两类均衡训练样本,构建训练集Ω．在检测分支中,从目标单元中提取特征向量,计算检测概率．图6中给出了4种检测器在10组数据下的检测结果,横轴表示数据名称．可以发现,检测概率最低的是基于Hurst指数的检测器[6],HH、HV、VH、VV极化下平均检测概率分别为0.248、0.351、0.351、0.290．这意味着该检测器无法探测到小目标,主要原因在于只利用了幅度信息,且观测时间未达到几秒以上．基于三特征的检测器[8]联合了时域和频域的特性,4种极化下的平均检测概率分别为0.534、0.622、0.619、0.518,性能得到大幅度提升．对于基于时频三特征的检测器[9],4种极化下的平均检测概率分别为0.698、0.699、0.698、0.614．相对于三特征的检测器[8]性能平均提升18%,特别是后5组数据,性能提升明显．对于提出的FAC-GBDT检测器,4种极化下的平均检测概率为0.774、0.777、0.789、0.733,相对于时频三特征的检测器[9]性能提升13%．此外,可以明显看到,FAC-GBDT检测器的检测概率在不同数据、不同极化下都具有最佳的性能．这主要源于检测器采用了7个特征,充分利用了多个域的信息,而且具有较好的稳健性能．

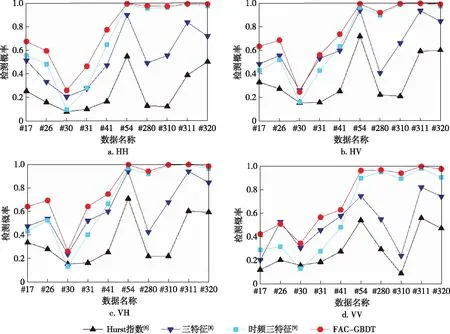
图6 4种检测器的性能对比(N=512,Pfa=10-3)Fig.6 Performance comparison between four detectors

下面,讨论观测时间对检测性能的影响．表2列出了N=512和N=1 024两种情况下的平均检测概率,对应观测时间为0.512 s和1.024 s．从表2中,得到以下3个结论:

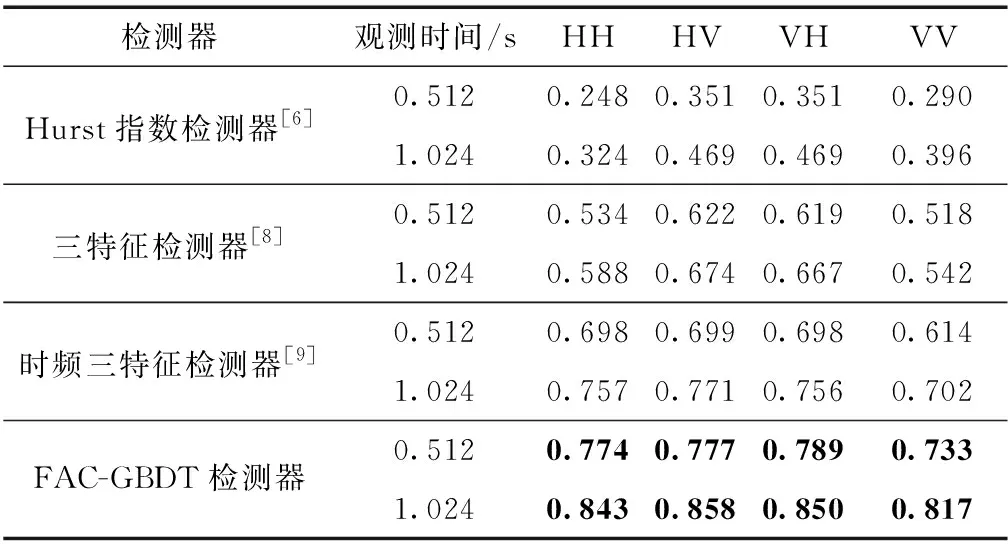
表2 不同观测时间下4种检测器性能对比

1)所有检测器在更长的观测时间下,检测性能均有所提升．这验证了长时累积是提升小目标的检测性能的有效途径．

2)FAC-GBDT检测器具有最优的检测结果,这是因为联合了时域、频域以及时频域的7维特征,能够充分利用海杂波和含目标回波在多域的差异性．

3)当观测时间增加1倍后,FAC-GBDT检测器没有其他3个检测器性能提升多．这是因为后5组数据的检测存在“天花板效应”．在观测时间为0.512 s时,FAC-GBDT检测器的检测概率已经接近于1,因此性能提升空间有限．

4 结论

本文提出一种高维特征域FAC-GBDT检测器,能充分利用时域、频域、时频域多个域的特征信息．通过将GBDT分类器的一类概率值作为统计量,能快速获得判决门限,解决了高维分类器虚警率难以控制的问题．后续可进一步优化分类器模型参数,满足海洋雷达在复杂海洋环境下稳健且快速探测的需要．