高压供油泵凸轮轴润滑特性的热流固耦合分析*

许 磊 张 翼 徐春龙 李斌茂 马运昌 唐诗泽 张 宇

(1.中北大学能源与动力工程学院 山西太原 030051；2.中国北方发动机研究所 天津 300400)

高压供油泵作为内燃机燃油供给系统的主要部件，在供油过程中，主轴、座圈等部件承受着大幅值的交变载荷，工作环境相对恶劣[1-2]。其中，柴油润滑用于减少曲轴轴颈摩擦副之间的磨损。柴油在零件表面附着一层微米级的油膜，既能避免零件间的相互接触，又能迅速带走摩擦产生的热量，其上油膜特性是影响零件寿命的一个重要方面[3-4]。宋兰兰[5]基于Reynolds提出的动压润滑理论，通过联立 Reynolds方程、黏温方程和能量方程分析了黏温效应影响下的滑动轴承动力特性及系统稳定性。由于考虑轴承表面粗糙度等影响因素的油膜能量方程过于复杂，文献[5]对能量方程进行了较大的简化，未能很好地反映表面油膜温度变化。PANG等[6]基于油膜厚度比理论，推导了润滑状态与扭矩载荷值的对应关系。主轴发生形变后对真实油液分布也有较大影响，杨东鹏[7]运用Workbench建立了液体动静压轴承油膜和轴瓦的流固耦合分析模型，采用单向流固耦合分析法研究了油膜的相关特性对轴瓦的应力变形情况所造成的影响。

在主轴工作时，主轴轴颈的旋转作用使得油膜对轴颈产生摩擦热，主轴内部油膜的平均温度会因此而升高[8]。当轴径内部温度升高后，黏温效应使得润滑油黏度降低，导致油膜产生的热量减少，同时由于润滑油黏度的降低使得润滑油流量增加，其端泄量增大，使得轴径得到更好的冷却，进而导致轴径的温度下降。故主轴内部油膜的热量及温度受到黏性耗散、润滑油黏温特性、润滑油通流特性的复杂耦合作用。柴油黏度较之于机油更小，受黏温效应影响，柴油黏度会更小，更易使摩擦副相对运动阻力增大，处于混合润滑和干摩擦概率增大，从而导致主轴损伤。故针对主轴采用柴油润滑时考虑黏温效应显得极为重要。

综上所述，学者们在结合能量方程求解油膜温度时，由于受多因素的影响能量方程过于复杂，均会对能量方程进行简化，而简化后的能量方程未必能反映真实的油膜温度。基于此，本文作者通过数学推导，建立一种可代入温度实验数据或导入软件计算温度数据的黏温效应一维计算仿真模型，以更好地反映真实的油膜温度；考虑到主轴内部油膜的热量及温度受多因素复杂耦合作用，主轴真实运转时油膜特性受主轴形变影响，建立Workbench平台下双向热流固耦合模型，研究黏温效应对主轴摩擦副油膜特性的影响；对黏温效应影响下柴油润滑主轴的油膜特性进行分析，为主轴设计提供依据。

1 MATLAB数值模拟

1.1 方程的量纲一化

计算流体动力学(CFD) 以计算机为载体，通过离散求解流动方程[9-10]。下文将根据离散求解流动方程的方式建立基于MATLAB的一维仿真模型。

常见的稳定运转的径向滑动轴承，其一般使用的雷诺方程二维形式如下式:

(1)

式中：p为油膜压力；h为油膜厚度；η为润滑油的动力黏度；U为轴颈旋转的线速度。

对式(1)进行量纲一化。采用x的量纲一化形式为：x=rφ→φ=x/r，0≤φ≤2π，其中φ为由轴与轴承中心连线沿轴旋转方向角度；r为轴承半径。采用z的量纲一化形式为：z=Lλ→λ=z/L，0≤λ≤1，其中L为轴承宽度；λ为量纲一轴承宽度。油膜厚度h的量纲一化形式为：H=h/c，其中H=1+εcosφ，ε=e/c，e为偏心量；c为轴承初始半径间隙；ε为偏心率；H为量纲一油膜厚度。对于压力p的量纲一化形式，先以一未定的p0值作为p的量纲一化数，则有：P=p/p0。

将以上量纲一化公式代入式(1)，并化简得：

(2)

(3)

式中：φ为由轴与轴承中心连线沿轴旋转方向角度；L为轴承宽度；n为转速；η为润滑油黏度。

U=2πnr，由此可得参考压力p0随转速升高而增加。

1.2 黏度变化的量纲一化方程

当考虑黏温特性影响时，轴承间隙流场内的黏度并非恒定，其黏度随温度变化曲线如图1所示。可见，黏度随流场温度变化而发生变化。对黏度求偏导时，其计算值不为0，原量纲一化方程改进为以下形式：

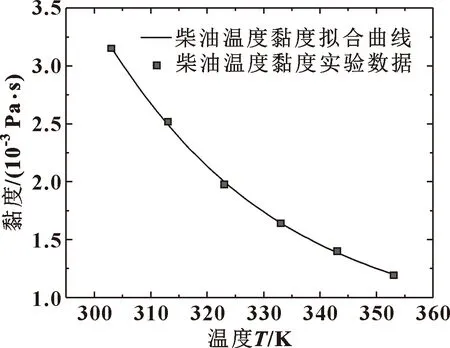
图1 柴油黏温特性曲线

(4)

其中计算黏度变化时采用基于柴油黏温特性实验数据[11]经由MATLAB拟合工具箱进行函数拟合后的函数关系式(5)，其中t为温度。

η=-5.97×10-9×(t-273)3+1.58×10-6×

(t-273)2-0.000 155 2×(t-273)+0.006 557

(5)

1.3 考虑黏度变化的Reynolds方程的差分形式

采用有限差分法求解油膜的压力分布，将轴承内部的油膜沿周向展开，设定周向和轴向的步长并为其划分网格，将 Reynolds方程转化为一组差分方程以此求得各节点的压力值。i方向的步长为Δφ，j方向的步长为Δλ。按差分原理，将油膜厚度H沿周向i的一阶差商等效为油膜厚度H在周向i的导数，如式(6)所示；将油膜压力P和黏度的差分形式等效为2个方向上的偏导数，如式(7)、(8)、(9)和(10)所示。

(6)

(7)

(8)

(9)

(10)

从而可以求得油膜压力P沿周向和轴向的二阶差商，并将其近似代替Reynolds方程中的二阶偏导数可得式(11)和式(12)。

(11)

(12)

将式(11)、(12)代入量纲一化处理后的Reynolds方程中，便可得到Reynolds方程的差分形式，经整理写成如下形式：

(13)

其中令：

E=A+B+C+D

F=6ηi,jΔφ(Hi+1/2,j-Hi-1/2,j)

推得计算压力分布的迭代公式如下：

(14)

超松弛迭代公式为

Pi,j=

(15)

其中取α=1.3。

基于以上差分方程可编写考虑黏温效应影响的油膜压力程序，建立基于MATLAB方法的仿真模型。该模型基于Reynolds方程的变形进行数学推导，实现可代入温度实验数据或导入软件计算的温度数据的黏温效应一维计算仿真模型。与传统方法简化的能量方程相比，该方法得到的能量方程包含表面粗糙度等复杂因素对温度的影响，能更好地反映实现油膜实际温度，计算结果与三维仿真结果吻合更好。文中将Fluent软件计算的温度数据导入一维计算仿真模型，完成后续一维仿真计算。

2 双向热流固耦合仿真方法

2.1 模型与网格

转子式高压供油泵凸轮轴的结构如图2所示，由座圈、凸轮轴和油膜3部分组成。挺柱产生的交变载荷作用于主轴套上的平面区域。位于主轴和座圈间的油膜厚度为0.05 mm。为提高仿真准确性，在0.05 mm厚度的油膜上划分5层网格。如图3所示，利用ICEM绘制流体域网格。油膜整体采用六面体网格，周向节点数496个，轴向节点数120个，网格总体质量达到0.75以上。经计算检验，当计算域网格总数为40万左右时，油膜最大压力、有效载荷计算值精度较好。

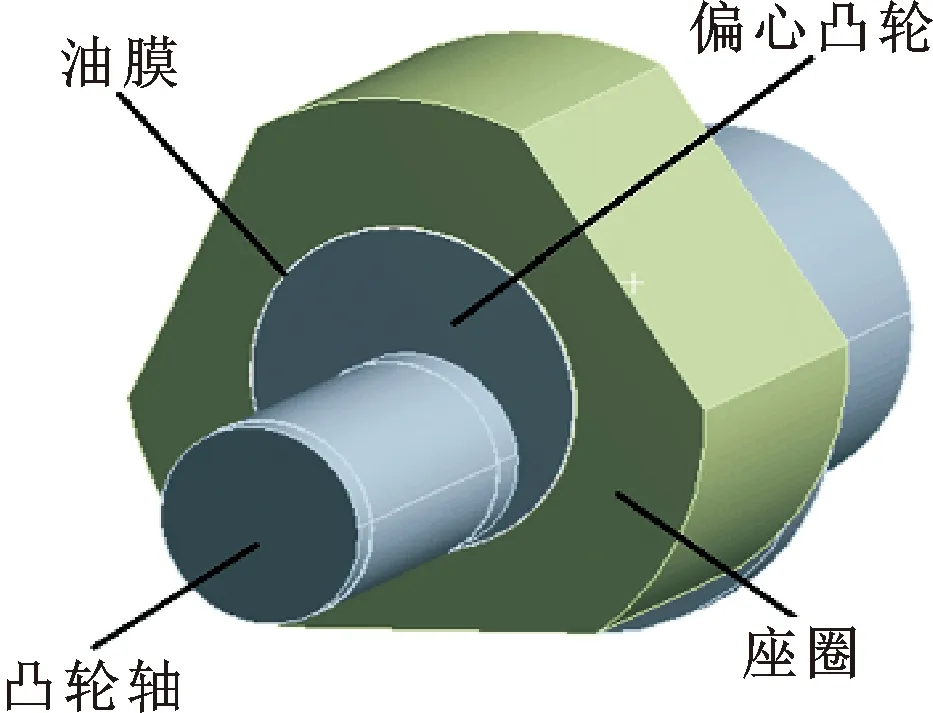
图2 凸轮轴仿真模型示意

图3 油膜网格示意

2.2 边界条件的设定

流体部分的边界条件根据实际情况在表1中给出。固体部分根据凸轮升程公式[12]算出弹簧随转角的压缩量，并结合座圈三面所承受柱塞压力，进一步计算得到交变载荷随时间变化的曲线如图4所示。

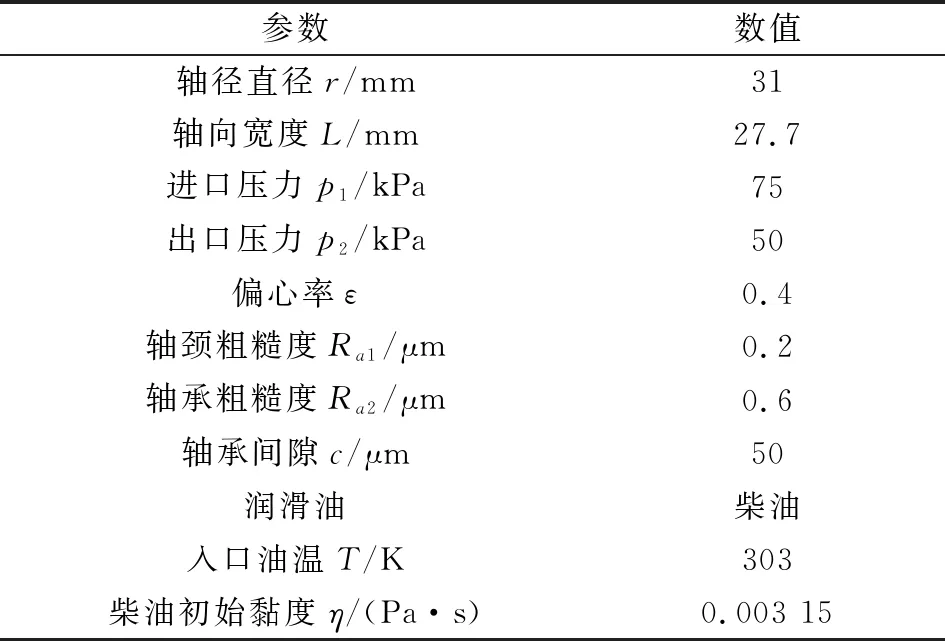
表1 油膜边界条件

图4 座圈三面压力随时间的变化曲线

主轴材料为20CrMnTi[13]，泊松比为0.25，材料密度为7 800 kg/m3，比热容为462 J/(kg·K)，弹性模量为207 GPa，热膨胀系数为1.27×10-5℃-1，导热系数为33.27 W/(m·K)。假设主轴与周围的空气传热为自然对流，复合传热系数为10 W/(m2·K)。环境温度为303 K。

2.3 双向热流固耦合仿真设定

在Ansys workbench中将Transient structural模块与Fluent模块用System coupling模块连接，分别在Transient structural与Fluent中导入固体网格与流体网格，并设置其边界条件；Fluent中湍流模型选择标准k-ε模型并勾选黏性发热，导入自编译UDF文件以模拟Fluent软件中黏度随温度的变化情况，采用由实验数据拟合后的函数关系式(5)。油膜初始偏心率为0.4，转速分别设置1 500、2 000、2 500 r/min。

在Ansys Workbench中的Transient structural模块输入apdl命令以开启多物理场耦合单元中的热固耦合单元，利用System coupling模块将其与Fluent中的流体域进行耦合，实现基于Ansys Workbench的双向热流固耦合。

3 有限元模型的验证

3.1 Fluent仿真及MATLAB模型验证

Fluent与MATLAB受黏温影响的压力计算结果如图5所示，其中Fluent仿真结果平面展开图基于Fluent仿真数据导出后由MATLAB程序重新绘制实现；另外，因MATLAB采用雷诺边界，没有负压区，故对Fluent仿真结果负压区进行了处理。

从图5可以看出，Fluent和MATLAB仿真计算的最大油膜压力基本相同，误差在2%以内，压力变化趋势基本一致。Fluent仿真结果中，压力峰值前的波动为油液进口处的压力冲击造成的；MATLAB仿真时，由于没有类似实际油膜的压力进口，使得计算结果存在误差。Fluent计算结果表明，随着转速的增加，油膜最大压力也会相应增加。通过MATLAB模型验证，Fluent仿真结果具有可靠性，为下文的双向热流固耦合计算及验证提供依据。

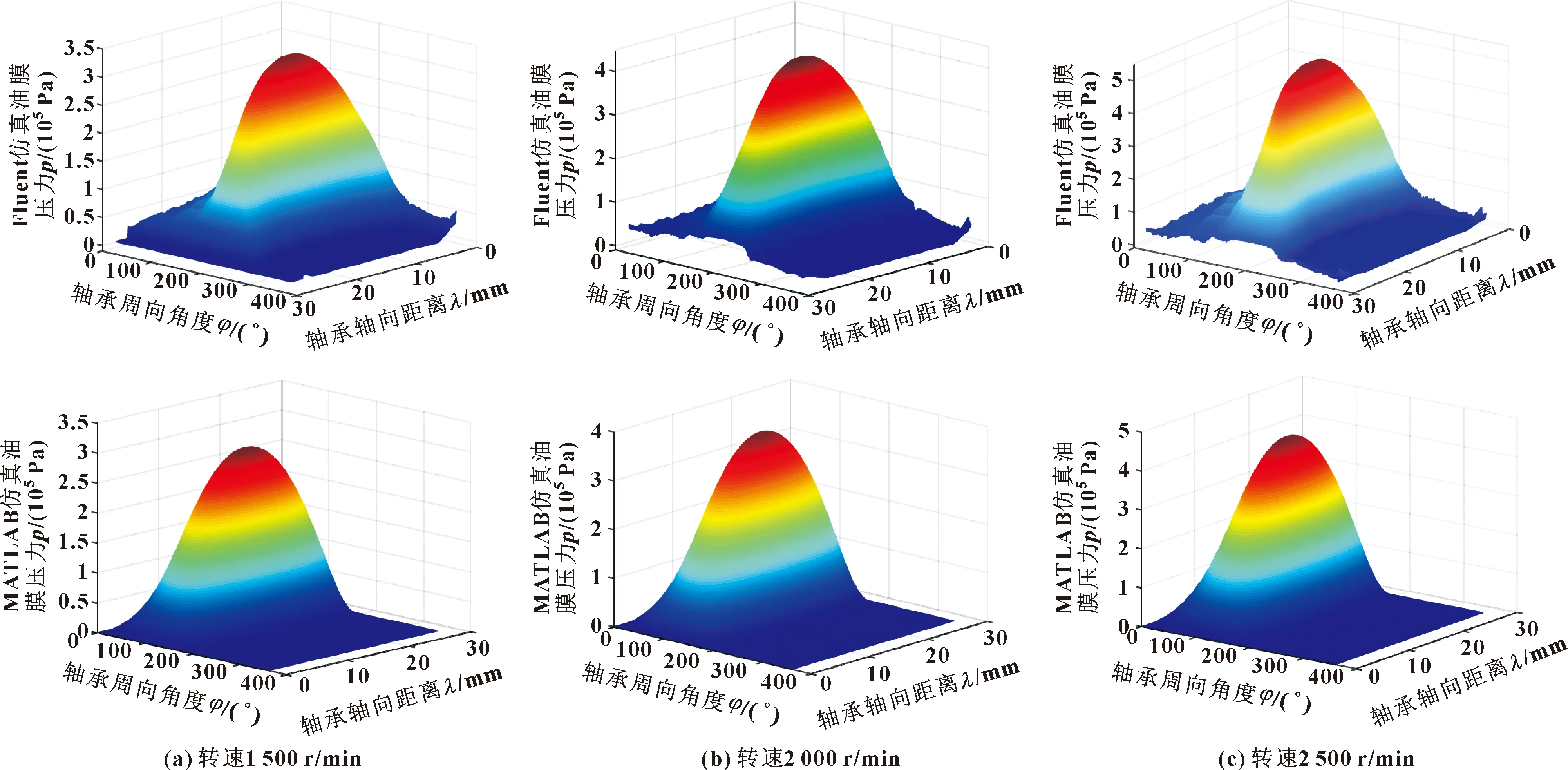
图5 不同转速下Fluent和MATLAB仿真结果对比

3.2 双向热流固耦合仿真结果验证

根据上述双向热流固耦合计算边界条件，分别在转速1 500、2 000、2 500 r/min下基于MATLAB模型对双向热流固耦合模型计算结果进行验证。热流固耦合与MATLAB受黏温影响的压力计算结果如图6、7所示。图7中针对未考虑黏温影响的热流固计算结果验证时，将MATLAB模型中黏温关系式改为常数，由于热流固耦合模型计算考虑了固体域形变对油膜的影响，因此造成了两模型计算结果的差异，但固体域形变很小，故影响甚微，两模型整体油膜压力变化趋势基本一致，验证了热流固耦合模型计算结果具有良好的可靠性。

图6 考虑黏温影响时不同转速下Fluent和MATLAB仿真压力对比

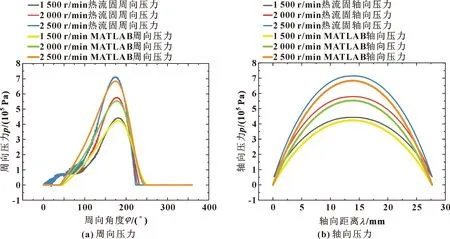
图7 不考虑黏温影响时不同转速下Fluent和MATLAB仿真压力对比

4 双向热流固耦合仿真及分析

4.1 忽略黏温效应与考虑黏温效应的双向热流固耦合计算结果及分析

如图8所示分别为1 500、2 000、2 500 r/min转速下油膜及主轴温度分布。当其他条件相同时[14]，油膜温度从中间向两端逐渐升高；主轴和油膜温度随主轴转速的增加而升高，呈对称分布；最高油膜温度处于偏心位置的边缘处。

图8 不同转速下油膜及主轴温度分布

如图9所示分别为1 500、2 000、2 500 r/min转速下忽略与考虑黏温效应的油膜压力分布。可以看出，当其他条件相同时，主轴油膜的压力随着主轴转速的增加而提高，同转速下受黏温效应影响压力会下降。3种转速下考虑黏温效应影响的油膜压力较之于忽略黏温效应的油膜压力，下降幅度分别为25.66%、27.56%、29.56%，随主轴转速增加，油膜压力受黏温效应的影响愈发显著。

图9 不同转速下忽略与考虑黏温效应油膜压力分布

如图10所示为3种转速下忽略与考虑黏温效应的主轴形变情况，总形变为热应变与油膜压力共同作用下的结果。

图10 不同转速下忽略与考虑黏温效应的主轴形变

由图10可见，主轴形变随主轴转速的增加略微升高；考虑黏温效应时，由于主轴油膜压力下降，主轴形变会略微降低；3种转速下考虑黏温效应的主轴形变较之于忽略黏温效应的主轴形变，下降幅度分别为0.10%、0.16%、0.26%。故考虑黏温效应时，主轴转速变化对主轴形变的影响很小。

4.2 忽略与考虑黏温效应时轴颈转速对油膜特性的影响

图11所示为忽略与考虑黏温效应时不同转速下的油膜特性分布。可以发现，当轴颈转速不断增加时，主轴内部油膜的承载力也会随之增加，这是因为随转速提升，柱塞传递给座圈的三面压力也会提高，且转速越大，动压效果越明显，承载能力越好[15]。承载力随主轴转速增加的关系近似为一条直线，且黏度恒定的油膜承载力要远大于考虑黏温效应的油膜承载力。这是因为，受黏度影响，润滑油不断消耗轴颈旋转所提供的机械能，不断转化为热量使油膜温度升高从而降低其黏度，导致润滑油流速加快从而降低了油膜的承载力；且转速越高，承载力降低越明显。

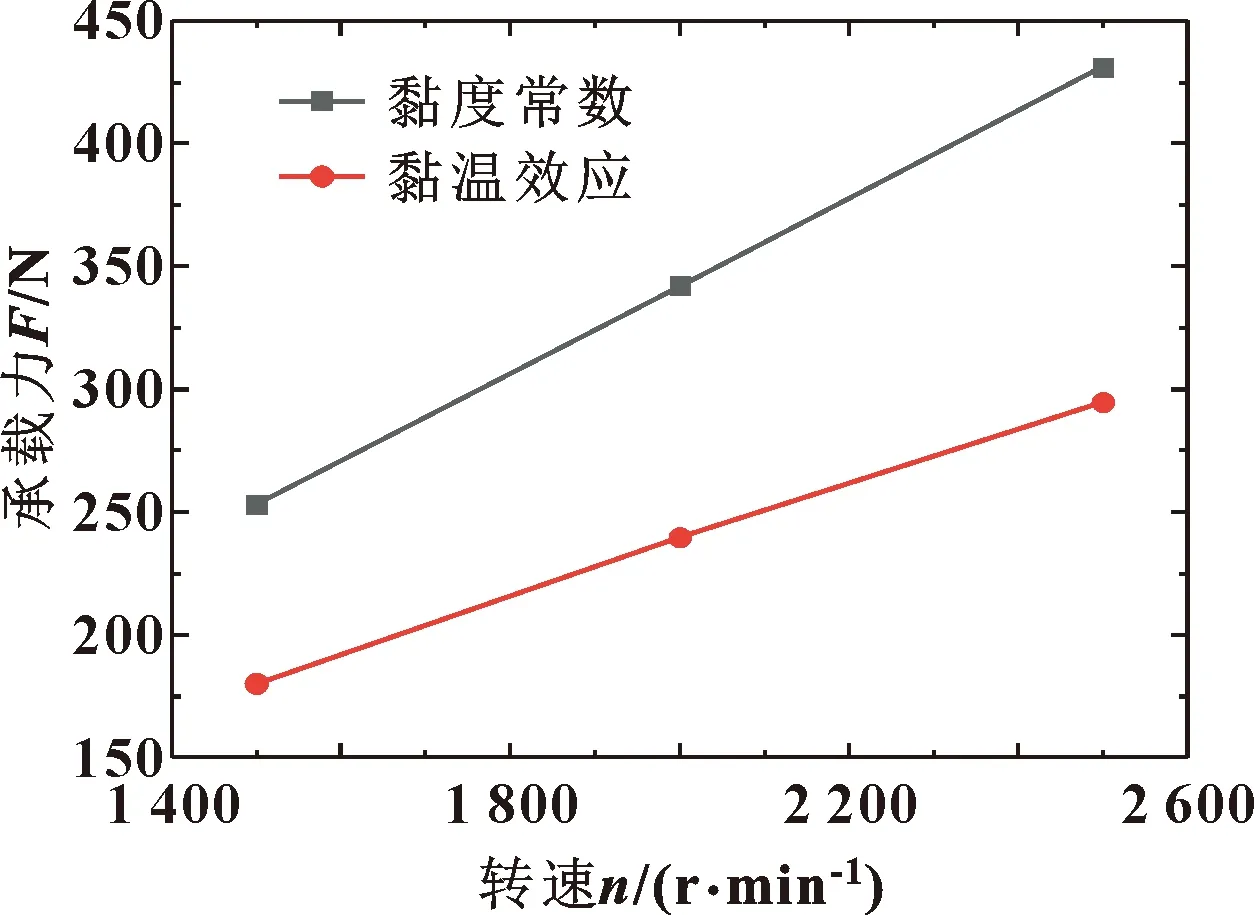
图11 忽略与考虑黏温效应时最大油膜承载力随转速的变化

图12所示为忽略与考虑黏温效应时最小油膜厚度随转速的变化。相较于油膜的承载力，油膜最小厚度随主轴转速变化较小，随主轴转速增加油膜最小厚度略微增加。最小油膜厚度受黏温影响略微减小，油膜由于受黏温影响所产生的黏性剪切应力减小，同油膜厚度下，黏度小的油膜所产生的油膜压力也较小，从而最小油膜厚度减小。

图12 忽略与考虑黏温效应时最小油膜厚度随转速的变化

图11、12的结果表明，不考虑柴油黏温特性的油膜承载力、最小油膜厚度均比考虑柴油黏温效应时高，而主轴在实际的工作过程中柴油的黏温效应是真实存在的，如果在主轴的设计环节忽略黏温效应，设计出的主轴轴径承载力将达不到预期效果，主轴实际工作中摩擦副的润滑形式处于混合润滑与边界润滑的概率增大，干摩擦概率增大，从而导致主轴损伤。

5 结论

(1)提出一种可代入温度实验数据或导入软件计算温度数据的黏温效应MATLAB一维计算仿真模型。与传统简化后的能量方程推导方法相比，该方法包含表面粗糙度等复杂因素对温度的影响，能更好地反映油膜实际温度，使计算结果与三维仿真结果有更好的对应。考虑黏温影响时采用MATLAB的油膜压力仿真结果与采用Fluent的油膜压力仿真结果变化趋势一致，最大相对误差2%，可作为考虑黏温影响的Fluent及油膜-主轴双向热流固耦合仿真结果的一种有效验证手段。

(2)考虑黏温效应影响时，随着转速增加，油膜压力、温度和承载力有显著增加，主轴的形变量和最小油膜厚度变化较小。转速增加导致的油膜温度升高会使润滑油黏度不均匀，进而导致主轴系统的失稳。因此，在主轴设计时，需设置主轴合理的工作转速以控制最高温升在允许范围内，保证主轴的热稳定性。

(3)随着主轴转速增加，黏温效应对油膜压力及承载力影响越趋明显，忽略黏温效应的油膜压力及承载力比考虑黏温效应影响的油膜压力及承载力普遍偏高，且随着转速增加，差值将更加明显。故高转速下油膜特性分析时，需要考虑黏温效应的影响，否则分析结果会偏高。如果在主轴的设计环节忽略黏温效应，设计出的主轴承载力将达不到预期效果，主轴在实际工作中发生干摩擦概率将增大，主轴易因承载能力不足而损伤。