一个指定验证者的基于身份可搜索认证加密方案

胡震宇，邓伦治，高 岩，施虹宇，武亚颖

(1.贵州师范大学 大数据与计算机科学学院，贵州 贵阳 550025；2.贵州师范大学 数学科学学院，贵州 贵阳 550025)

0 引言

如今，信息技术的发展带来了数据量的迅速膨胀，对于各种机构和网络个人用户，云存储服务的广泛应用成为一种必然趋势。虽然云存储的使用极大方便了数据的管理和分享，但是上传到云服务器上的数据面临丢失、恶意修改和泄露的风险，因此上传到云服务器上的数据常为加密数据。大量的加密数据带来了密文检索困难的问题，而对所有密文进行解密并在明文上进行检索不符合现实需求。因此，在密文上进行检索是一项必要的研究内容。

为了解决密文检索问题，Song等[1]在2000年提出了可搜索加密(Searchable encryption,SE)的概念并给出了一个具体方案。在可搜索加密体制中，存在数据发送者、数据接收者和云服务器(即数据验证者)3个实体。数据发送者将作为加密文件索引的关键词密文与该文件一同上传至云服务器。在检索密文时，数据接收者对所需文件关键词生成搜索陷门并提交给云服务器，云服务器使用验证算法验证搜索陷门是否与现存关键词密文匹配，若匹配成功则返回搜索陷门所成功匹配关键词密文对应的文件，否则搜索失败。在检索过程中，关键词明文信息不会被泄露。但文献[1]的方案是一个对称加密方案，由此带来的密钥分配复杂性使其不适合数据分享情景。为此，Boneh等[2]在2004年提出了第一个公钥可搜索加密(Searchable public key encryption,SPE)。之后，Baek 等[3]进一步提供了一个无安全信道的SPE框架，数据接收者可以通过公共信道向服务器发送搜索陷门。但是为了认证用户公钥，基于传统公钥设施构建的SPE方案需要一个第三方可信机构来为用户发放证书。由此，Abdalla等[4]扩展了Shamir[5]提出的基于身份公钥密码学概念，提出一个基于身份的可搜索加密(Identity-based SE,IBSE)方案，在该密码体制中，私钥生成中心(Private key generator,PKG)利用用户的身份信息(如工号、证件号码、姓名等)为用户生成公钥和私钥，省去了证书发放的问题。随后，一系列基于身份的可搜索加密方案被提出。[6-7]

由于日常语言习惯，用来作为加密文件索引的关键词空间较小。当截获一个关键词搜索陷门时，拥有匹配测试权限的敌手可以利用数据接收者的公钥为所有可能的关键词生成关键词密文并尝试与所截获陷门匹配，直到成功为止。这种攻击被称为关键词猜测攻击(Keywords guessing attacks,KGA)[8-9]。抵御KGA的一种可行方案是指定验证者，即只有被指定的实体才能进行匹配测试算法。但是该方法必须保证指定验证者是可信的，否则其仍可进行如上描述的关键词猜测攻击。为了解决这个问题，Huang等[10]提出了可搜索认证加密(Searchable authenticated encryption,SAE)概念。在该类方案[10-11]中，关键词加密算法要用到数据发送者的私钥，因此只有数据发送者才能生成有效密文。2019年，Li等[12]提出了一个指定验证者的基于身份可搜索认证加密(Designated tester identity-based SAE,DIBSAE)，在该方案中，只有指定验证者才能进行匹配测试算法，但指定验证者无法生成有效密文来进行KGA，即可以抵御内部关键词猜测攻击。

在依赖随机谕言模型的安全性证明中，哈希函数被一个人为构造的列表所替代，此类方案在现实中可能是不安全的[13-14]，而标准模型允许通过直接运算哈希函数来获得哈希值，因此在现实中有更高的安全性。本文提出了一个基于强安全模型的DIBSAE方案并在标准模型下证明了其安全性。另外，由于新方案不使用双线性对运算和哈希到点运算，因此该方案与同类方案相比具有更高效率。

1 准备知识

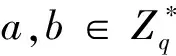
2 方案定义

本节我们将给出本方案的方案模型和安全性模型。

2.1 方案模型

一个DIBSAE方案由如下5个多项式时间算法组成：

1)系统参数生成算法Setup：输入安全参数δ，PKG通过此算法生成并公布系统参数parm。

2)用户密钥生成算法UserKeyGen：输入系统参数parm、实体地址IDi，PKG利用此算法为用户IDi生成并发送公钥RIDi和私钥dIDi。

3)关键词密文生成算法dIBSAE：输入全局参数parm、数据发送者地址IDS及其私钥dIDS、数据接收者的地址IDR及其公钥RIDR、指定验证者地址IDdS及其公钥RIDdS和索引关键词w,数据发送者IDS通过该算法生成关键词密文Cw作为相关加密文件的索引与该文件一起上传指定服务器IDdS。

4)搜索陷门生成算法Trapdoor：输入全局参数parm、数据发送者地址IDS及其公钥RIDS、数据接收者地址IDR及其私钥dIDR、指定验证者地址IDdS及其公钥RIDdS和搜索关键词w′,数据接收者IDR利用该算法输出搜索陷门Tw′。

5)匹配测试算法MatchTest：输入全局参数parm、数据发送者地址IDS、数据接收者地址IDR、指定验证者地址IDdS及其私钥dIDdS、关键词密文Cw和搜索陷门Tw′，指定服务器IDdS通过该算法输出结果"0"或"1"。其中，"0"代表搜索失败，"1"代表搜索成功。若搜索成功，IDdS将对应加密文件发送给数据接收者IDR。

2.2 安全性模型

本部分我们将给出dIBSAE方案的安全模型。

在DIBSAE中存在内部和外部两类敌手，其分别定义为：

1)AO(外部敌手)：具体指除指定服务器IDdS之外的任何人。

2)AI(内部敌手)：具体指指定服务器IDdS。

一个DIBSAE方案应该满足在关键词猜测攻击下的关键词密文不可区分性(Ciphertext indistinguishability under the keyword guessing attacks,CIND-KGA)和在关键词猜测攻击下的陷门不可区分性(Trapdoor indistinguishability under the keyword guessing attacks,TIND-KGA)。这两类安全性分别保证多项式敌手无法通过关键词猜测攻击从关键词密文和搜索陷门中获得有用的关键词信息。

CIND-KGA和TIND-KGA以如下几个对抗游戏定义。

定义2 (CIND-KGA)没有多项式时间敌手AO或AI可以以不可忽略的优势赢得以下游戏，则称一个dIBSAE方案满足CIND-KGA。

游戏1 (针对AO的CIND-KGA)挑战者C与dIBSAE中的敌手AO进行如下游戏：

初始化挑战者C设置安全参数δ，输出主密钥s和系统参数parm并发送parm给AO。

第一阶段本阶段敌手AO适应性地向挑战者C做一系列查询，具体描述如下：

UPK-Query：当AO提交实体IDi时，C返回IDi的公钥RIDi。

SK-Query：当AO提交IDi时，C返回IDi的私钥dIDi。

dIBSAE-Query：AO提交元组(IDS,IDR,IDdS,w)时，C返回发送者为IDS，接收者为IDR，指定验证者为IDdS的关于关键词w的关键词密文Cw。

TD-Query：当AO提交元组(IDS,IDR,IDdS,w)时，C返回发送者为IDS，接收者为IDR，指定验证者为IDdS的关于关键词w的搜索陷门Tw。

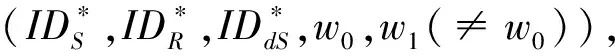
猜测敌手AO提交ω′，若ω′=ω，则称敌手AO在游戏1中获胜。

敌手AO在游戏1中的优势被定义为：

游戏2 (针对AI的CIND-KGA)挑战者C与dIBSAE中的敌手AI进行如下游戏：

初始化挑战者C设置安全参数δ，输出主密钥s和系统参数parm并发送parm给AI。

第一阶段本阶段敌手AI适应性地向挑战者C做一系列如游戏1中AO可做的查询。

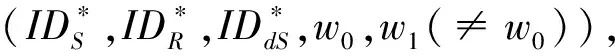
第二阶段AI继续进行一系列第一阶段的各项操作，条件是：

猜测敌手AI提交ω′，若ω′=ω，则称敌手AI在游戏2中获胜。

敌手AI在游戏2中的优势被定义为：

定义3 (TIND-KGA)没有多项式时间敌手AO和AI可以以不可忽略的优势赢得以下游戏，则称一个dIBSAE方案满足TIND-KGA。

游戏3 (针对AO的TIND-KGA)挑战者C与dIBSAE中的敌手AO进行如下游戏：

初始化同游戏1。

第一阶段同游戏1。

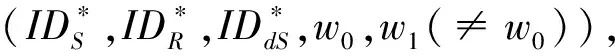
猜测敌手AO提交ω′，若ω′=ω，则称敌手AO在游戏3中获胜。

敌手AO在游戏3中的优势被定义为：

游戏4 (针对AI的TIND-KGA)挑战者C与dIBSAE中的敌手AI进行如下游戏：

初始化同游戏2。

第一阶段同游戏2。

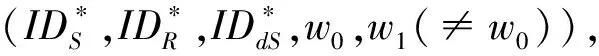
第二阶段AI继续进行一系列第一阶段的各项操作，条件是：

猜测敌手AI提交ω′，若ω′=ω，则称敌手AI在游戏4中获胜。

敌手AI在游戏4中的优势被定义为：

3 方案描述

3.1 具体方案

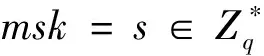
公布系统参数parm=(δ,q,G,P,P0,h0,h1,h2,h3)。

(3)DIBSAE(parm,IDS,dIDS,IDR,RIDR,IDdS,RIDdS,w)：输入元组(parm,IDS,dIDS,IDR,RIDR,IDdS,RIDdS,w)，数据发送者IDS做如下操作：

2)计算C1=tP，

μ=h1(IDS,IDR,IDdS,dIDS(RIDR+αIDRP0),w)，

ρ=t(RIDdS+αIDdSP0)，

C2=h2(C1,IDS,IDR,IDdS,ρ,μ)。

3)输出关键词密文Cw=(C1,C2)。

(4)Trapdoor(parm,IDS,RIDS,IDR,dIDR,IDdS,RIDdS,w′)：输入元组(parm,IDS,RIDS,IDR,dIDR,IDdS,RIDdS,w′)，数据接收者IDR做如下操作：

2)计算T1=l1P，ρ′=l1(RIDdS+αIDdSP0)，

μ′=h1(IDS,IDR,IDdS,dIDR(RIDS+αIDSP0),w′)，

T2=l2h3(T1,IDS,IDR,IDdS,ρ′)，T3=l2+μ′。

3)输出搜索陷门Tw′=(T1,T2,T3)。

(5)MatchTest(parm,IDS,IDR,IDdS,dIDdS,Cw,Tw′)：输入元组(parm,IDS,IDR,IDdS,dIDdS,Cw,Tw′)指定服务器IDdS做如下操作：

1)计算h=h3(T1,IDS,IDR,IDdS,dIDdST1)，θ1=dIDdSC1，θ2=T3-T2h-1。

2)验证C2=h2(C1,IDS,IDR,IDdS,θ1,θ2)是否成立。若等式成立，输出结果"1"，否则，输出结果"0"。

3.2 正确性

θ1=dIDdSC1=(rIDdS+αIDdSs)tP=t(RIDdS+αIDdSP0)=ρ,dIDdST1=(rIDdS+αIDdSs)l1P=l1(RIDdS+αIDdSP0)=ρ′,dIDR(RIDS+αIDSP0)=dIDRdIDSP=dIDS(RIDR+αIDRP0),θ2=T3-T2h-1=μ′。

易知，当w′=w时C2=h2(C1,IDS,IDR,IDdS,θ1,θ2)成立，因此本方案是正确的。

4 安全性证明

定理1 在DDH问题下，新方案满足CIND-KGA，该定理将分引理1和引理2在标准模型下证明。

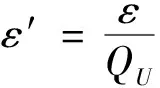
证明假设有一个DDH问题的元组(P,aP,bP,X)，C将在游戏1中担当挑战者来判断X=abP是否成立。

初始化输入安全参数δ，C通过Setup算法生成主密钥s和系统参数parm=(δ,q,G,P,P0,h0,h1,h2,h3)然后发送系统参数parm给AO。

第一阶段C对AO所做的一系列如下操作进行回应。在A的每一次其他查询前都需要进行UPK-Query。C维护几张初始为空的列表来存储查询和回复(该要求在本节均适用)。

UPK-Query：C维护元组形式为(IDi,rIDi,RIDi)的列表LU，当AO输入IDi时，C在列表LU中查找(IDi,RIDi)并返回RIDi。如果没有对应条目，C做如下操作：

1)在第j次创建条目时，C添加(IDj,⊥,aP)到LU。

SK-Query：当AO提交IDi时，若IDi=IDj，游戏中止。否则，C通过调用UserKeyGen算法返回dIDi给AO。

dIBSAE-Query：当AO提交(IDS,IDR,IDdS,w)，C调用dIBSAE算法得到Cw并将其返回给AO。

TD-Query：当AO提交(IDS,IDR,IDdS,w)，C调用Trapdoor算法得到Tw并将其返回给AO。

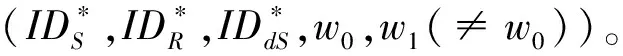
2)计算

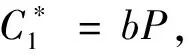
第二阶段AO可以在满足游戏1要求的情况下重新进行第一阶段中的各项查询。

猜测AO输出ω′，如果ω′=ω，则称AO在游戏1中获胜。

解决DDH问题如果AO获胜C输出"1"，否则输出"0"。如果X=abP，有

ρ=X+αIDjsbP=b(aP+αIDjP0)

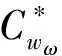
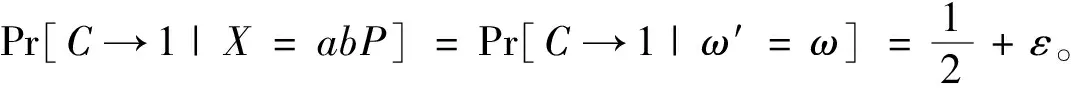
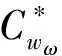
概率分析 令QU，QSK分别为UPK-Query，SK-Query的次数，一些事件定义如下：

E1：AO没有对IDj进行SK-Query。

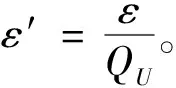
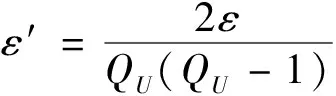
证明假设有一个DDH问题的元组(P,aP,bP,X)，C将在游戏2中担当挑战者来判断X=abP是否成立。

初始化 输入安全参数δ，C通过Setup算法生成主密钥s和系统参数parm=(δ,q,G,P,P0,h0,h1,h2,h3)然后发送系统参数parm给AI。

第一阶段C对AI所做的一系列如下操作进行回应。

UPK-Query：C维护元组形式为(IDi,rIDi,RIDi)的列表LU，当AI输入IDi时，C在列表LU中查找(IDi,RIDi)并返回RIDi。如果没有对应条目，C做如下操作：

1)在第j次创建条目时，C添加(IDj,⊥,aP)到LU。

2)在第k(≠j)次创建条目时，C添加(IDk,⊥,bP)到LU。

SK-Query：当AI提交IDi时，若IDi∈{IDj,IDk}，游戏中止。否则，C通过调用UserKeyGen算法返回dIDi给AI。

dIBSAE-Query：当AI提交(IDS,IDR,IDdS,w)，C做如下操作：

1)当IDS∉{IDj,IDk}时,C调用dIBSAE算法得到Cw并将其返回给AI。

2)当IDS∈{IDj,IDk}但IDR∉{IDj,IDk}时，C获取Cw的方法同dIBSAE算法，但μ的算法变为：

μ=h1(IDS,IDR,IDdS,dIDR(RIDS+αIDSP0),w)，然后C将Cw返回给AI。

3)当{IDS,IDR}={IDj,IDk}时，C输入(IDdS,w)，调用挑战阶段的IC算法获得Cw并将其返回给AI。

TD-Query：当AI提交(IDS,IDR,IDdS,w)，C做如下操作：

1)当IDR∉{IDj,IDk}时,C调用Trapdoor算法得到Tw并将其返回给AI。

2)当IDR∈{IDj,IDk}但IDS∉{IDj,IDk}，C获取Tw的方法同Trapdoor算法，但μ′的算法变为：

μ′=h1(IDS,IDR,IDdS,dIDS(RIDR+αIDRP0),w)，然后C将Tw返回给AI。

3)当{IDS,IDR}={IDj,IDk}时，C输入(IDdS,w)，调用挑战阶段的IT算法获得Tw并将其返回给AI。

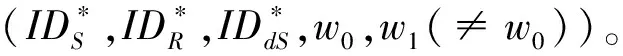
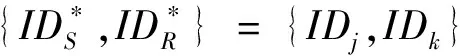
IC(IDdS,w)→Cw：该算法用于在当{IDS,IDR}={IDj,IDk}时针对指定验证者IDdS输出关键词w的密文，为方便表示，此处我们假设IDS=IDj，IDR=IDk，C做如下操作：

1)在列表LU中找出(IDj,aP)，(IDk,bP)和(IDdS,RIDdS)。

2)计算

αIDj=h0(IDj,aP)，αIDk=h0(IDk,bP)，

αIDdS=h0(IDdS,RIDdS)。

C1=tP，ρ=t(RIDdS+αIDdSP0)，

τ=X+αIDksaP+αIDjsbP+αIDkαIDjsP0，

μ=h1(IDj,IDk,IDdS,τ,w)，

C2=h2(C1,IDj,IDk,IDdS,ρ,μ)。

4)输出密文Cw=(C1,C2)。

IT(IDdS,w)→Tw：该算法用于在当{IDS,IDR}={IDj,IDk}时针对指定验证者IDdS输出关键词w的搜索陷门，为方便表示，我们假设IDS=IDj，IDR=IDk，C做如下操作

1)在列表LU中找出(IDj,aP)，(IDk,bP)和(IDdS,RIDdS)。

2)计算

αIDj=h0(IDj,aP)，αIDk=h0(IDk,bP)，

αIDdS=h0(IDdS,RIDdS)。

T1=l1P，ρ′=l1(RIDdS+αIDdSP0)，

τ′=X+αIDjsbP+αIDksaP+αIDkαIDjsP0，

μ′=h1(IDj,IDk,IDdS,τ′,w)，

T2=l2h3(T1,IDj,IDk,IDdS,ρ′)，T3=l2+μ′。

4)输出陷门Tw=(T1,T2,T3)。

第二阶段AI可以在满足游戏2要求的情况下重新进行第一阶段中的各项查询。

猜测AI输出ω′，如果ω′=ω，则称AI在游戏2中获胜。

解决DDH问题如果AI获胜C输出"1"，否则输出"0"。如果X=abP，有

τ=X+αIDksaP+αIDjsbP+αIDkαIDjsP0

=(a+αIDjs)(bP+αIDkP0)

概率分析令QU，QSK分别为UPK-Query，SK-Query的次数，一些事件定义如下：

E1：AI没有对IDi∈{IDj,IDk}进行SK-Query。

定理2 在DDH问题下，新方案满足TIND-KGA，该定理将分引理3和引理4在标准模型下证明。

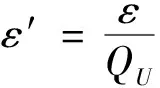
证明假设有一个DDH问题的元组(P,aP,bP,X),C将在游戏3中担当挑战者来判断X=abP是否成立。

初始化同引理1。

阶段1 同引理1。

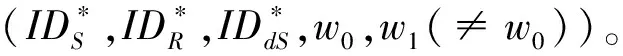
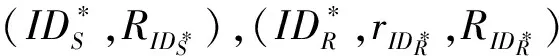
2)计算

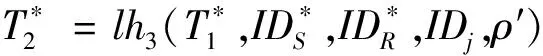
第二阶段AO可以在满足游戏3要求的情况下重新进行第一阶段中的各项查询。

猜测AO输出ω′，如果ω′=ω，则称AO在游戏3中获胜。

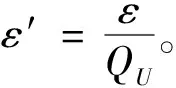
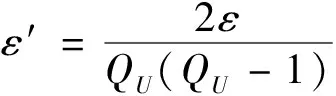
证明假设有一个DDH问题的元组(P,aP,bP,X)，C将在游戏4中担当挑战者来判断X=abP是否成立。

初始化同引理2。

第一阶段同引理2。

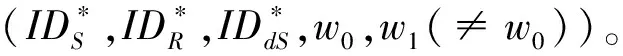
第二阶段AI可以在满足游戏4要求的情况下重新进行第一阶段中的各项查询。

猜测AI输出ω′，如果ω′=ω，则称AI在游戏4中获胜。

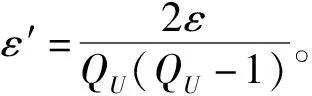
5 性能对比

本节我们将新方案与另外3个指定验证者的基于身份可搜索加密方案进行性能对比。

安全性方面，我们基于本方案提出的安全模型对新方案和对照方案进行安全性对比，其结果见表1。

表1 安全性对比

效率方面，我们将算法每运行1次的各项运算时间总和作为效率指标，主要统计了新方案与对比方案中所用到的成本较高的3种运算，包括双线性对(Bilinear pairing,BP)运算、哈希到点(Hash-to-point,H)运算和标量乘法(Scalar multiplication,SM)运算。为了保证对比的公正性，我们使用了第三方数据，Lu等[11]中通过模拟实验得出上述3种运算的单次时间成本分别为：TBP=4.154 ms，TH=4.362 ms，TSM=1.631 ms。具体的对比结果见表2。

表2 计算开销(毫秒)

6 结论

本文提出了一个指定验证者的基于身份可搜索认证加密方案，算法中不使用高成本运算，因此与同类方案相比具有更高效率。另外，本文在标准模型下证明了新方案的安全性，所有哈希值都通过直接计算哈希函数得到，且新方案基于更强的安全模型，因此在现实中有更高的安全性。