调和映射的Schwarz导数与对数导数的新定义及其范数

谭俊键，杨 敏

(西华师范大学 数学与信息学院，四川 南充 637000)

0 引言

本文重新定义了平面调和映射的Schwarz导数和对数导数，并对新定义下的Schwarz导数和对数导数的范数进行了研究。解析函数的Schwarz导数和对数导数的范数与单叶性有密切的联系。1932年，Kraus[1]证明了局部单叶解析函数在单位圆盘上单叶的必要条件。1949年，Nehari[2]不仅通过面积定理也证明了Kraus[1]的结果，还证明了解析函数在单位圆盘上单叶的充分条件。1979年，对于解析函数在单位圆盘上单叶的充分条件，Nehari[3]给出了一般化的结果。1984，Clunie和Sheil-Small[4]证明了一个关于解析函数单调性的定理，该定理在研究平面调和映射的Schwarz导数的范数方面有着很重要的应用。随后，Chuaqui等[5-7]对解析函数的Schwarz导数和对数导数及其范数进行了更广泛而深入的研究。

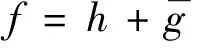
设φ是单位圆Δ内的局部单叶解析函数。它的对数导数φ和Schwarz导数φ定义为：

(1)

(2)

(3)

(4)

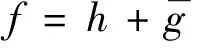
(5)

(6)

(7)

(8)

其中λ=|h′|+|g′|。

1 对数导数的新定义

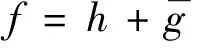
(9)

因为

从而

(10)

同理可得

(11)

又因为

ωh′=g′，g″=ω′h′+ωh″

(12)

所以根据(10)～(12)式得到

将此代入(9)式，得到

(13)

又因为

(14)

根据(5)、(13)和(14)式可得

(15)

其中Pf即为对数导数的定义。

此时令ω=q2，则

因此

(16)

2 Schwarz导数的新定义

根据(6)和(15)式可得：

(17)

又因为

(18)

根据(14)式可得

将此代入(18)式可得

(19)

又因为

(20)

根据(6)、(17)、(19)和(20)式可得

Sf=

(21)

其中Sf即为Schwarz导数的新定义。

此时令ω=q2，则

Sf=

(22)

当f是解析函数时q=0，所以Sf=Sh。即符合解析函数的Schwarz导数的定义。

3 新定义下对数导数范数的有界性

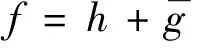
证明由对数导数的新定义(16)式和三角不等式可得

(23)

由Schwarz-pick引理可知，在单位圆内有

(24)

且Pommerenke在文[13]中得到

(25)

将(24)和(25)式代入(23)式得到

(26)

‖Pf‖≤C2<∞

(27)

4 新定义下Schwarz导数范数的有界性

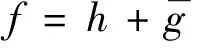
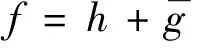
(28)

经过计算可得

(29)

由(2)式可得

(30)

由(13)式和(21)式可知，当λ=|h′|+t|g′|，t∈[-1,1]时，有

Pf=

(31)

对单位圆盘上任意一个z0，令Pf(z0)=μθ(z0)，则有

(32)

‖Sf‖≤6

(33)

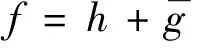
证明Sh表示单位圆上的单叶保向调和映射，其中f(0)=h(0)=g(0)=h′(0)-1=0。设f为单位圆上的单叶保向调和映射，则当

(34)

使得φ(0)=z0，且

其中

(35)

因为

S(f1 ° g)=Sf1[g(z)]·(g′)2+Sg

且当f为调和Möbius变换时，Sf=0。所以

S(f1 ° φ)=Sf1[φ(z)]·(φ′(z))2

(36)

当z=0时，根据(34)、(35)和(36)式可得

(37)

因为Sf是Möbius不变的，所以

(38)

又因为z0为单位圆上任意一点，所以

(39)

由文[14]中的定理9可知，若f1∈Sh，f为单叶调和映射，则fR(z)=f(Rz)在单位圆上为单叶凸调和函数。利用(33)式和链式法则可得

R2|Sf(0)|=|SfR(0)|≤6

(40)

所以

(41)

由Schwarz导数的新定义(22)式和三角不等式可得

(42)

将(41)、(24)、和(25)式代入(42)式得到

(43)

(44)

再次利用Schwarz导数的新定义(22)式和三角不等式可得

<∞