圆环在抛物面上运动模式的分析与探讨

凌一凡，刘 阳，刘玉洁，卢礼萍

(1. 南京农业大学 理学院，江苏 南京 210095；2. 南京农业大学 金融学院，江苏 南京 210095)

刚体运动普遍存在于日常生活中. 从旋转的小行星和人造卫星，到斜坡上滚动的球与自行车轮子的动力学，许多日常现象都可以从刚体运动的角度来理解. 其中，理论研究较为成熟的是经典的欧拉盘问题[1]. 在水平面上释放一薄圆盘，圆盘会沿着一定的轨迹滚动前进，其进动速率越来越大，而盘面与水平面的倾角越来越小，直至停止运动. 根据刚体的运动方程，在无摩擦和无约束条件下，圆盘停止运动前的进动速率将发散至无穷大. 但事实并非如此，圆盘运动过程中总会存在接触面的摩擦和空气阻力，导致进动速率最终变为零. 由此许多针对该运动的耗散理论被提出，但是确切的机理至今仍未明确. 由于圆环的中空结构允许空气流过，其受到的空气阻力与圆盘不同. 特别是在倾角较小的情况下，两个体系的空气动力学存在明显差异，因而两者在运动轨迹上有所区别[2].

此外，物体在曲面上的运动也是人们普遍关注的研究方向. 例如硬币漏斗，即从双曲线型漏斗的表面溜槽内发射一枚硬币，它会顺着双曲面滚动前进，其轨道半径越来越小，最后终止在漏斗底部. 这一运动成立的条件是硬币直径比漏斗直径小得多. 当硬币或者圆环的直径增加，或者不使用溜槽，让硬币以任意角度开始运动，其运动轨迹会更加复杂，类似花瓣. 部分观点认为漏斗中的运动轨迹与漏斗的形状有关，并证明了任何表面都不可能形成除圆外的任何开普勒轨道[3]. 本文在二次曲面上以不同初速度方向发射圆环，获得不同的运动模式，接着利用现有的轨迹方程拟合实验结果，验证运动模式与初速度之间的关联；最后应用刚体理论对几种特殊的运动模式的角动量进行了探讨.

1 圆环在抛物面上的运动模式

实验中，选用圆底锅代替抛物面，见图1(a)，经过测量曲面函数为

(1)

建立如图1(b)所示的抛物面坐标. 圆环的材质包括塑料、金属、木质等. 在尝试了不同种类材质圆环后，发现材质对圆环运动轨迹的影响不大，而环直径、初速度方向以及重量是决定环轨迹的重要因素. 因此本文采用质量较小的细金属环(半径1.5 cm) 来比较不同初速度方向下的运动轨迹. 图2(a)为三叶草运动模式，图2(b)为该模式在x和y方向上的运动.

圆底锅

tracker软件追踪到的圆环在抛物面上的质心运动轨迹

为了更好地对比不同初速度方向的运动轨迹，本文利用Tracker对每个环运动视频进行了跟踪并记录相关运动数据，再使用Matlab模拟出的与实际圆锅参数一致的二次曲面，对所得轨迹坐标进行了运动重构，结果见图3. 设θ为初速度方向与抛物面直径之间的夹角,如图2(a). 当θ=0°时，圆环运动轨迹类似沿着直径的一条直线，当θ=20°时为细长的三叶草形；θ=40°时，为短胖的三叶草；而θ=50°时，则为螺旋的同心圆. 尽管在角度变化中无法准确控制初速度的大小，但多次实验的结果具有可重复性，因此有关初速度方向的实验结论仍然是可靠的. 此外，本文还发现初速度的大小只能改变圆环同一次运动轨迹z轴的高度，即影响三叶草的轨迹范围，而不影响运动模式.

θ=0

2 质心运动学描述

由上述实验可知，圆环在抛物面上运动时，其运动轨迹类似三叶草形状，每片叶子的胖瘦取决于圆环的初速度方向，而直线型和螺旋型轨迹是其中两个特例. 由此利用五角星的轨迹方程构建本实验中的运动方程为

x=Acos(ω1t+φ1)+Bcos(ω2t+φ2)

(2a)

y=Asin(ω1t+φ1)-Bsin(ω2t+φ2)

(2b)

(3a)

(3b)

采用最小二乘法将上述运动方程拟合三叶草运动模式图3(b)和螺旋同心圆模式图3(d)，得到各个参数值见表1. 图4(a)和4(b)是拟合的图3(b)的轨迹，图4(c)和4(d)是拟合的图3(d)的轨迹. 这里值得指出的是，虽然方程(3)能很好的描述三叶草和螺旋同心圆的运动模式，但是无法描述直线型图3(a)的运动模式.

表1 方程(3)拟合三叶草和圆形图3(b)和(d)所得的参数

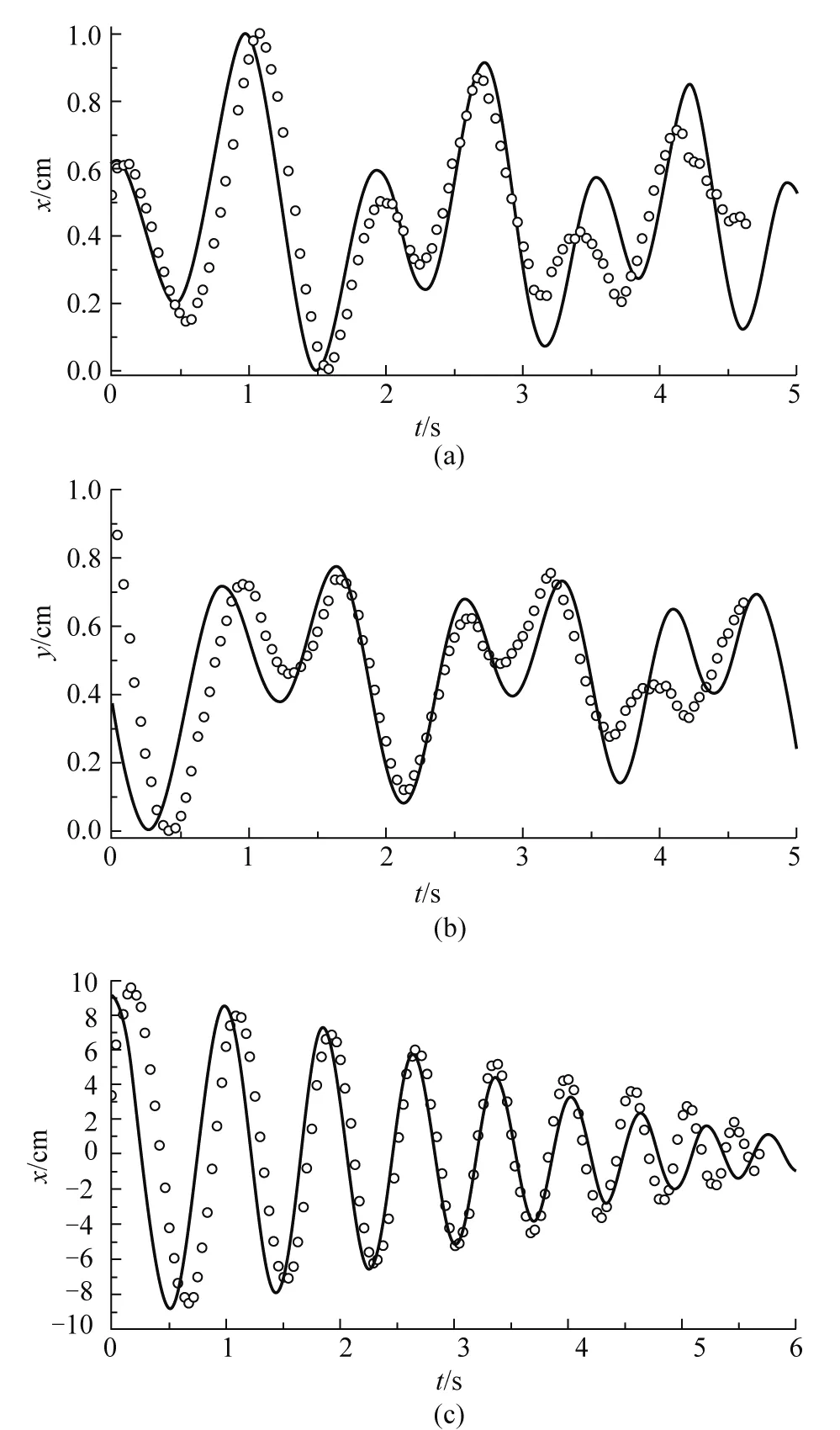
图4 根据方程(3)拟合的运动轨迹，图中圆圈代表实验数据，曲线代表拟合结果. (a)和(b)是三叶草运动模，(c)和(d)是螺旋同心圆运动模

3 初速度分析

由上述分析可知，方程(3)可以用来描述圆环在二次曲面的大部分运动轨迹. 为了简化计算过程，用简化的方程(2)来讨论运动初速度问题. 对运动方程x分量和y分量分别求导数，即可得到环在x、y方向的速度方程为

υx=-ω1Asin(ω1t+φ1)-ω2Bsin(ω2t+φ2)

(4a)

υy=ω1Acos(ω1t+φ1)-ω2Bcos(ω2t+φ2)

(4b)

取t=0，ω1∶ω2=1∶2，则初速度方向为

(5)

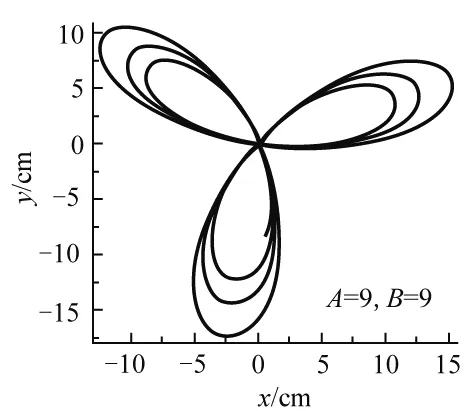
A/B=1

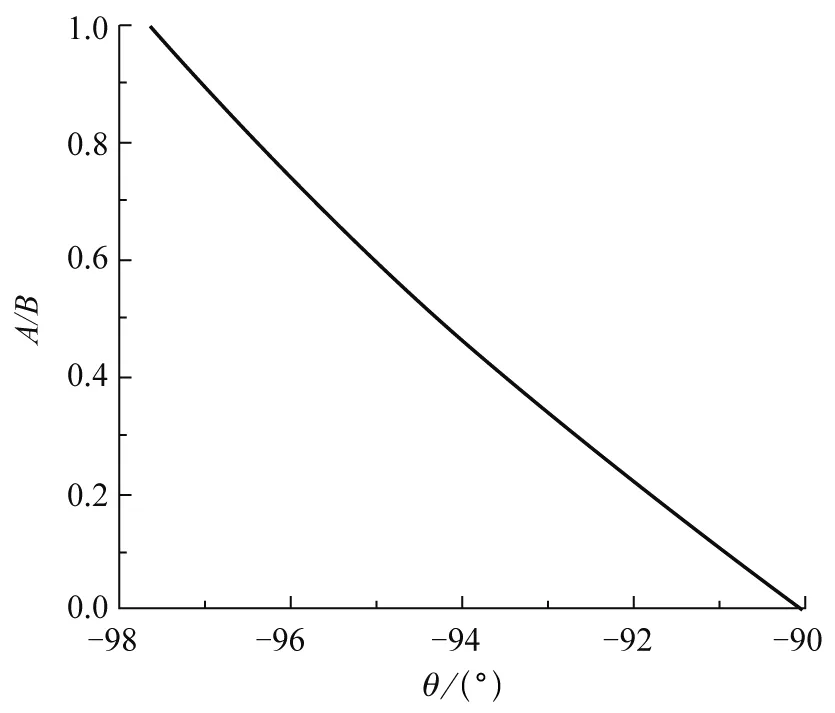
图6 利用方程(5)所得到的与初速度方向的关系. 计算中夹角θ为初速度方向与x轴正方向的夹角，因此图像的横坐标为负值

4 转动问题讨论

图7 圆环在平面上运动的示意图. 以环的质心建立坐标系轴为穿过曲面中心的竖直轴线. Ω为进动角速度，α为倾角，ω1为自转角速度

利用两种坐标的转换，圆环的总角速度可以表示为[4]

(6)

再利用环与底面接触点速度为零的约束条件，该速度为质心速度加上相对于质心的相对速度，则

vcon=vcm+ω×a=0

(7)

结合式(6)、(7)可得质心速度为

(8)

质心平动方程为

(9)

质心角动量定理为

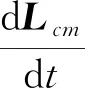
(10)

式(9)、(10)合并，消去受力项，得到三个分量为[4]

(11)

将上述3个分量用于本实验运动的讨论.

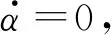
(12)

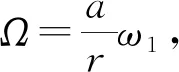
(13)

图8(b)是不同倾角α时，圆环在逐渐下落的过程中(a=1 cm)，随着半径r的减小，Ω逐渐增加，当r接近零时，则Ω可趋于无穷大. 图中一个特例为当α=π/2时，Ω始终为零. 然而在图3(d)的同心圆运动模式中，当圆环到达抛物面底部时，任何一种速度都降低到零. 因此本文认为，虽然这种情况适合于描述本实验中图3(d)的运动形式，但是不适合描述同心圆轨迹收尾时的运动，因为当圆环接近抛物面底部时，圆环不断与抛物面碰撞和反弹，此时α不再为一常数. 当圆环进行三叶草运动模式时，则倾角α和半径r均为衰减的周期变化函数，此时讨论式(11)变得相当复杂，这里不再做进一步讨论.

圆环在曲面螺旋运动示意图

5 结论

为了研究圆环在抛物面上的运动模式，实验中将圆环以不同初速度方向入射，通过Tracker软件跟踪运动轨迹获得不同运动模式，即直线型、三叶草型和螺旋同心圆型. 利用现有的运动方程并考虑到实际运动情况，构建衰减模式的三叶草运动方程，探讨了不同初速度方向与运动模式之间的关联. 结果发现当初速度方向与抛物面直径方向夹角θ较小时，运动轨迹呈细长型三叶草；随着夹角的θ的增加，三叶草形状变丰满，最后转变为螺旋的同心圆. 最后利用刚体运动的理论体系，探讨了特殊运动模式下圆环的转角速度.

而在其他研究中，人们则从平动角度出发，将圆环视为质点，对环不同的椭圆轨迹建立了相关微分方程，进行动力学分析，并在受力分析的基础上构建了动能理论方程，进行能量分析.研究重点是阐述摩擦力和初速度对圆环轨道运动的影响，得到的结论是摩擦力影响轨迹重复次数和最后围绕中心点的振动次数，初速度则影响环的轨道重复次数，而并不影响振动次数[5]. 但研究对环转动方面的相关运动并未进行相关的研究. 实际的刚体运动是一个复杂运动体系. 虽然目前对圆环的刚体运动已经存在许多相关的理论解释，但精确且完整的理论体系仍有待深入研究. 本文通过现有的理论框架，结合现代化的软件和设备，实现理论与实验的可视化结合，较为合理地解释了刚体在特定曲面的部分运动模式.