一种改进的樽海鞘群算法*
郑洪清,谢 聪,周永权
(1.广西职业师范学院教育学院,广西南宁 530007;2.广西农业职业技术大学,广西南宁 530007;3.广西民族大学人工智能学院,广西南宁 530006)
群智能算法在许多领域发挥着重要的作用,近年来各种受自然界生物群体行为启发的群智能算法被提出,如布谷鸟搜索(Cuckoo Search,CS)算法[1],灰狼优化(Grey Wolf Optimizer,GWO)算法[2]和鲸鱼优化算法(Whale Optimization Algorithm,WOA)[3]等。Mirjalili等[4]根据樽海鞘群的觅食行为提出一种樽海鞘群算法(Salp Swarm Algorithm,SSA),因其原理简单和易于实现,已成功应用于多个领域[5,6]。然而,樽海鞘群算法与其他群智能算法一样,必须克服求解精度低和易陷入局部最优等缺点。诸多学者针对这一缺陷提出各种改进策略,如白钰等[7]提出基于自适应惯性权重的樽海鞘群算法,引入惯性权重和差分变异思想提高算法性能;陈连兴等[8]提出一种改进的樽海鞘群算法,对领导者引入加权重心取代最优个体位置和对个体逐维随机差分变异,改进了算法的寻优性能,但这两种算法的Rosenbrock函数求解精度较低。张铸等[9]提出基于自适应正态云模型的引力樽海鞘群算法,结合引力搜索技术和正态云发生器有效提高收敛精度,全局搜索能力大大增强,但局部搜索能力相对较弱。王彦军等[10]提出改进的樽海鞘群算法及其在焊接梁问题中的应用,利用精英反向学习、差分策略和Gauss变异为算法全局搜索奠定基础;康俊涛等[11]提出基于樽海鞘群算法的桁架结构优化设计,在搜索过程中引入个体历史信息改进算法,但算法改进效果不明显。周新等[12]提出融合黄金正弦混合变异的自适应樽海鞘群算法,通过黄金正弦算法(Golden Sine Algorithm,Gold-SA)替换樽海鞘群算法领导者位置更新方式,并融合邻域重心反向学习与柯西变异,改善算法性能,测试函数较为简单。范千等[13]提出一种改进的樽海鞘群算法,采用折射反向学习机制和自适应控制因子提高优化性能;陈忠云等[14]提出基于混沌精英质心拉伸机制的樽海鞘群算法,采用Tent混沌和精英质心拉伸机制增强全局搜索能力;张严等[15]提出基于Levy飞行策略的改进樽海鞘群算法,对领导者位置进行Levy飞行更新,但以上算法求解精度较低。
虽然上述改进算法与基本SSA相比在性能上有了一定程度的改善,但求解精度还有提升空间。因此,本研究提出一种改进的樽海鞘群算法(Improved Salp Swarm Algorithm,ISSA),通过在追随者阶段引入差分进化策略和黄金正弦机制,共同增强算法寻优能力。通过23个基准函数测试,验证ISSA算法的有效性。
1 樽海鞘群算法
樽海鞘群算法是模拟樽海鞘群觅食行为而衍生的一种群智能算法,在SSA中领导者引导群体进行食物搜索,其位置更新公式为
(1)
c1=2e-(4×l/lmax)2,
(2)
其中,Fj表示第j维领导者位置;c1是平衡全局搜索和局部搜索的重要参数,在迭代前期c1值较大有利于全局搜索,在迭代后期c1值较小有利于局部搜索;c2,c3∈[0,1];ubj,lbj表示第j维的上下界;l表示当前迭代次数;lmax表示最大迭代次数。
追随者紧随领导者后并依次形成链式结构,其位置更新公式为
(3)
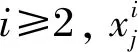
2 改进的樽海鞘群算法
2.1 改进领导者方式
基本SSA中,领导者完全依靠式(1)进行搜索,若领导者陷入局部最优,则追随者必陷入局部最优。因此考虑对领导者第j维值采用随机维度以拓展种群多样性,有利于算法跳出局部最优,故领导者位置更新公式修改为
k=randperm(n),
(4)
(5)
其中,n为问题维数,randperm为生成不重复的随机整数。
2.2 改进追随者方式
在基本SSA中,当前追随者位置仅取自身位置和上一个位置的平均值,若追随者紧密相连,则不利于全局搜索,且未利用群体之间的交流信息,因此考虑对追随者采用差分进化策略进一步拓展种群多样性。首先剔除种群中领导者位置,从剩下种群中随机生成3个不同位置的追随者进行差分进化操作,具体计算公式如下:
(6)
其中,r1,r2,r3为追随者中任意一个,且r1≠r2≠r3,b∈[0,1]为控制变异概率。
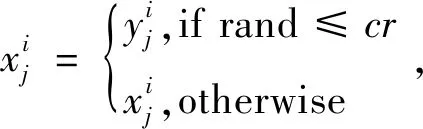
(7)
其中,cr∈[0,1]为控制交叉概率。
2.3 黄金正弦算法
黄金正弦算法是Tanyildizi等[16]提出的一种元启发式算法,该算法基于正弦函数和单位圆的关系求解优化问题。Gold-SA遍历单位圆上所有点,因而具有较强的全局搜索能力,而且在全局最优位置和当前位置采用黄金分割系数,因此也具有较强的局部搜索能力。Gold-SA位置更新公式为
(8)
其中,r1∈[0,2π]内的随机数,r2∈[0,π]内的随机数,x1=-π+(1-τ)×2π,τ为黄金分割系数,
x2=-π+τ×2π。为进一步提升Gold-SA局部搜索能力,在自身位置引入自适应惯性权重式(2),因此最终Gold-SA位置更新公式为
(9)
2.4 ISSA伪代码
输入:种群规模N,函数名称及最大迭代次数,设置变异概率b和交叉概率cr,计算黄金分割系数。
①在领域范围内随机产生初始种群,计算其最优值及食物源位置。
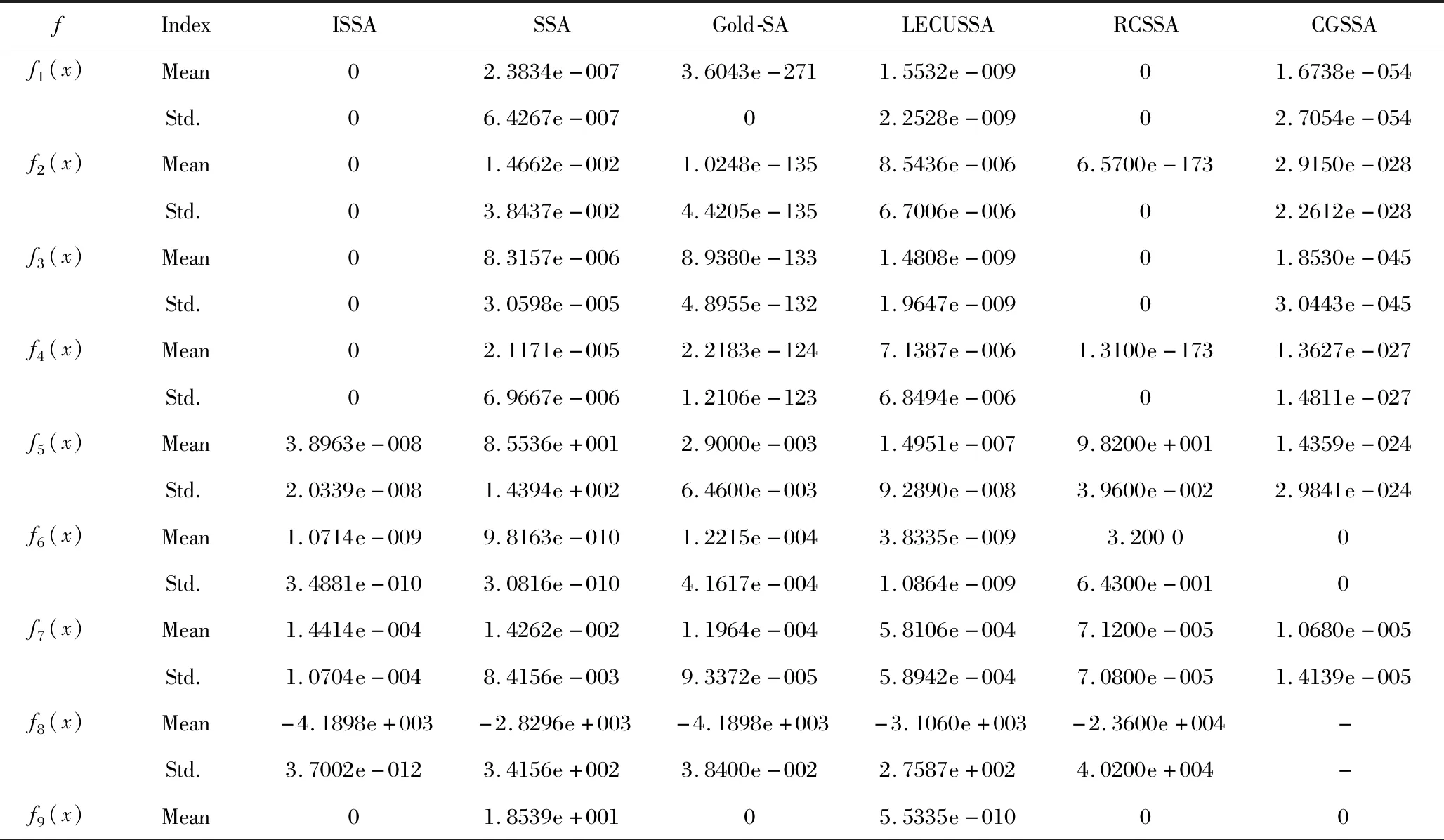
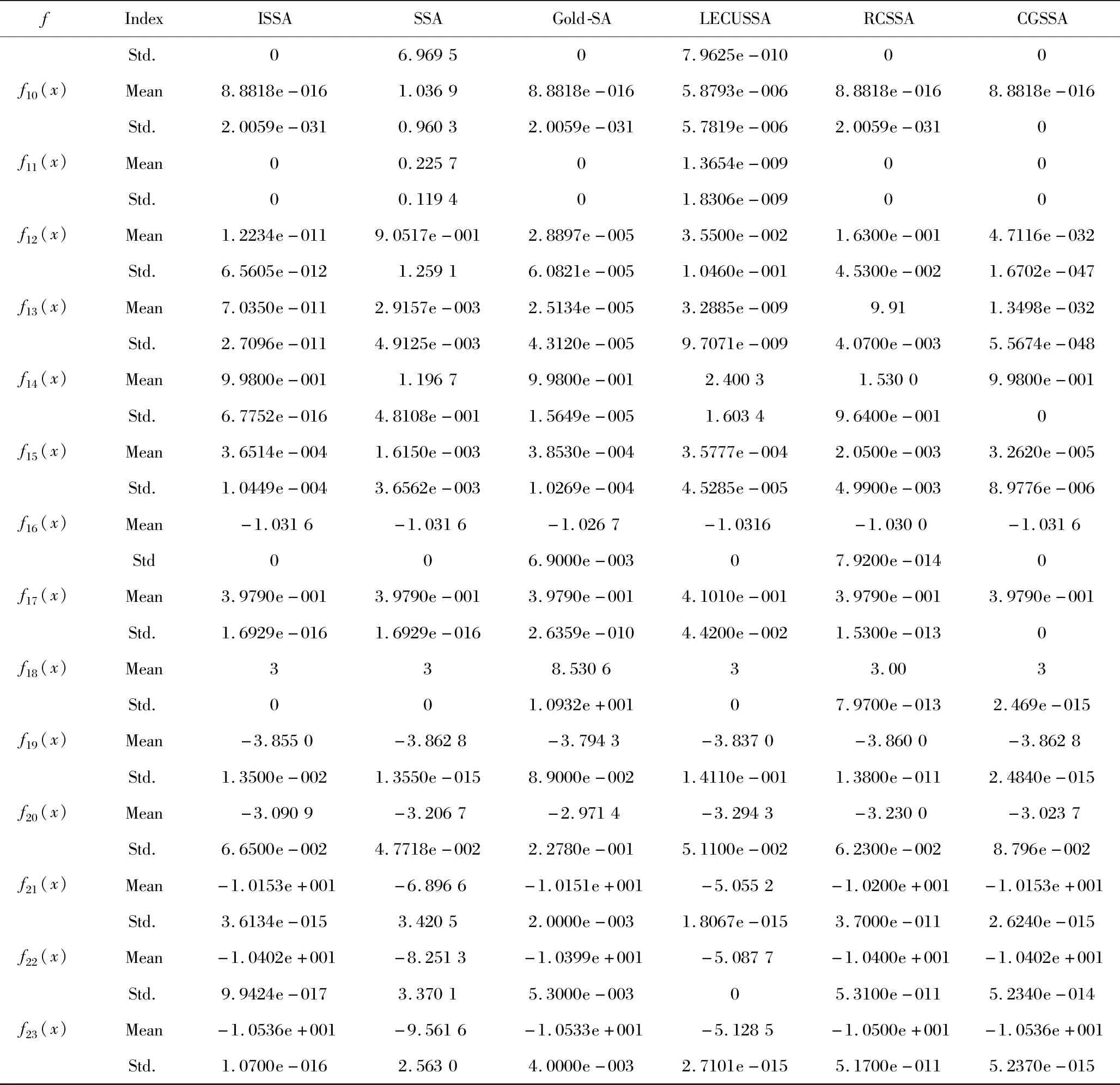
②Whilel ③ 计算式(2); ④ Fori=1∶N ⑤ Ifi≤N/2i ⑥ 执行式(4)、式(5); ⑦ Else ⑧ If rand ⑨ 执行式(6)、式(7); (3)氧化锌回收技术仍需改进,火法回收应注重解决生产过程中能耗高且氧化锌纯度较低等问题,还应注重解决回转窑内结圈问题。酸法回收过程产生的废酸回收处理有待研究,氨法回收过程中产生的氨气直接排放造成大气污染,因此回收并处理氨气也是氨法回收氧化锌的重要研究内容 ⑩ Else 在ISSA中只是一定概率下执行式(6)、式(7)和式(9),并替换基本SSA中的式(3),因此并没有增加算法的时间复杂度。 为检验ISSA的性能,选取文献[9]中23个基准函数进行测试,并将其计算结果与基本SSA、Gold-SA和改进算法LECUSSA[15]、RCSSA[13]及CGSSA[9]进行比较,以验证ISSA综合改进策略的效果。为公平比较,所有算法的参数设置如下:N=30,lmax=500,b=0.2,cr=0.1,其余参数设置与原文献相同。每种算法在Matlab 2016a软件中独立运行30次,计算每个函数的平均值(Mean)和方差(Std.),Mean和Std.越小,则性能越佳,结果如表1所示。 表1 基准函数的实验结果Table 1 Experimental results of benchmark functions 续表Continued table 从表1可知,ISSA与基本SSA和Gold-SA比较,在7个单峰函数(f1-f7)测试下,ISSA的计算结果除函数f6比SSA、函数f7比Gold-SA差且相差甚微以外,其余5个函数的计算结果均优于SSA和Gold-SA,其中函数f1-f4达到理论值,函数f5的计算结果分别比Gold-SA和SSA高出5个和9个数量级,可见ISSA局部勘探能力优异。在6个多峰函数(f8-f13)测试下,ISSA的计算结果都优于SSA,有3个函数的计算结果与Gold-SA相等,有3个函数的计算结果优于Gold-SA,可见ISSA全局搜索能力更强。在10个固定维多峰函数(f14-f23)测试下,ISSA的计算结果除函数f19和f20比SSA稍差以外,大多数函数的计算结果均优于SSA或Gold-SA,证明ISSA全局搜索能力优异。 再将ISSA与改进算法LECUSSA、RCSSA及CGSSA进行比较,LECUSSA仅函数f15、f20求解结果比ISSA优越且差别不大,其余21个函数中有2个函数(f16、f18)求解结果与ISSA一致,另外19个函数求解结果均比ISSA算法差;RCSSA有5个函数(f1、f3、f9、f10、f11)求解结果与ISSA一致,有3个函数(f7,f19,f20)求解结果优于ISSA,其余函数求解结果均比ISSA差;除函数f8外,CGSSA有8个函数(f1-f4、f18、f20、f22、f23)求解结果比ISSA差,有3个函数(f9、f11、f16)求解结果与ISSA相等,其余11个函数求解结果优于ISSA。因此,总体来看,ISSA优于LECUSSA和RCSSA,次于CGSSA。 为直观展示ISSA的收敛速度和计算精度,给出部分函数平均收敛曲线如图1所示;为便于比较,纵坐标取平均函数值对数。从图1可知,ISSA的平均收敛曲线速度比SSA快,计算精度比SSA高;但在迭代前期ISSA收敛速度慢于Gold-SA,这是由于在迭代前期ISSA以大概率执行差分进化策略,而在迭代后期ISSA收敛速度明显优于Gold-SA。 图1 函数收敛曲线Fig.1 Convergence curve of function 本研究提出了一种改进的樽海鞘群算法,通过在领导者位置引入随机维度以拓展种群多样性。在算法前期,追随者以较大概率执行差分进化策略,进一步增强种群多样性;在算法后期,追随者以较大概率执行黄金正弦算法,同时在黄金正弦算法自身位置引入自适应惯性权重增强局部勘探能力。使用23个基准函数评估算法,结果表明ISSA寻优性能优于基本SSA和Gold-SA,同时与其他改进的樽海鞘群算法相比,ISSA算法也具有一定优势。2.5 ISSA时间复杂度分析
3 仿真实验与结果
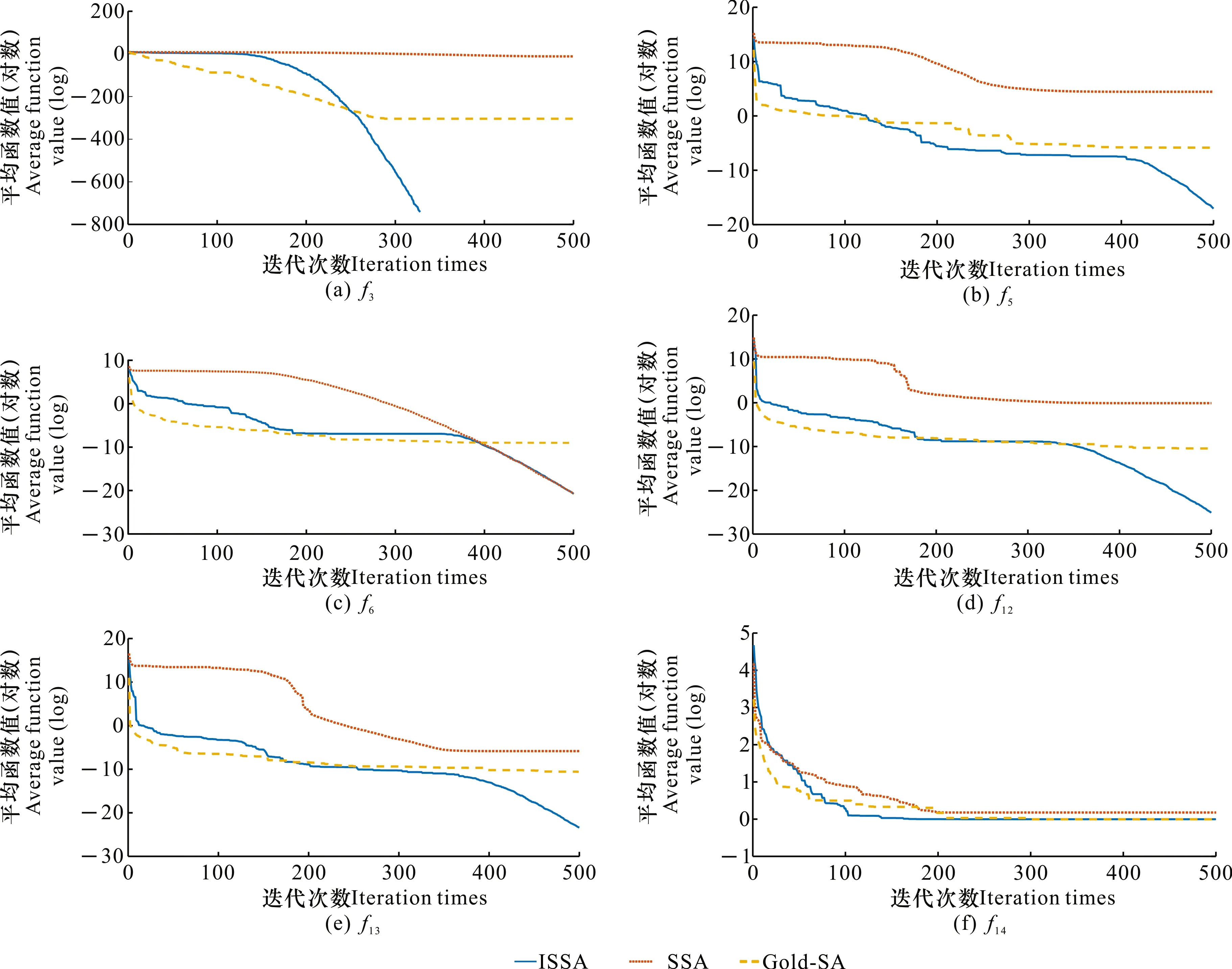
4 结论

