基于Cirq的Deutsch-Jozsa电路综合算法
戴 娟,李志强,杨冬晗
(扬州大学信息工程学院,江苏 扬州 225100)
0 引言
Deutsch-Jozsa算法作为第一个量子算法,首次实现了对经典算法的指数级加速,解决了n个量子比特的Deutsch问题,奠定了量子算法的基本思想[1]。一般的经典算法处理问题需要做2n-1+1次,而Deutsch-Jozsa算法只需要一步就可以完成。与经典算法相比,量子算法融入了量子力学的很多特征,比如量子的相干性、量子叠加性、量子并行性、纠缠性等等。这些物理性质很大程度上提高了计算的效率,使该算法具有更快的运算潜能[2]。
此前,很多学者研究了Deutsch-Jozsa算法的电路实现及其应用。Cheng等[3]研究了如何模拟Deutsch-Jozsa电路,Xie等[4]研究了Deutsch-Jozsa的复杂性,Cheng等[5]实现了利用四能级超导量子干涉仪实现Deutsch算法,Zhang等[6]研究了量子Fourier变换在实现Deutsch-Jozsa算法中的应用。但是,还未见针对Deutsch-Jozsa算法的电路综合算法的详细报道。研究Oracle电路的构建、Deutsch-Jozsa电路的综合对解决Deutsch问题至关重要。本文在利用Cirq源码研究1比特Deutsch电路的基础上,研究构建n比特Oracle电路,从而综合Deutsch-Jozsa算法的电路,进而对其进行模拟。
1 Deutsch-Jozsa算法
Deutsch问题给定一个承诺,函数f(x)要么是常数函数要么是平衡函数。构造Deutsch-Jozsa电路,通过测量可以判断这个函数是常数函数还是平衡函数[7]。
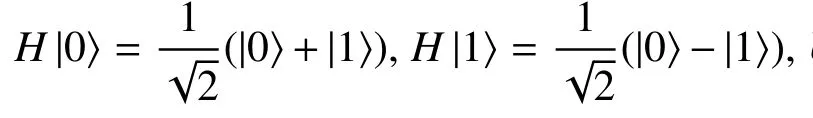
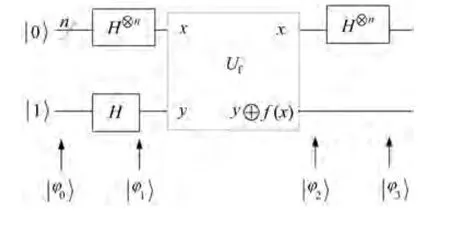
图1 Deutsch-Jozsa电路图Fig.1 Schematic diagram of Deutsch-Jozsa circuit
输入状态为 |φ0〉=|0〉⊗n|1〉。Deutsch-Jozsa 算法的实现步骤如下:
第1步把n+1个Hadamard门分别作用在每一个量子比特上,得到

第2步通过Uf,对这n+1个量子比特操作,得到

第3步将n个Hadamard门分别作用在前n个量子比特上,得到

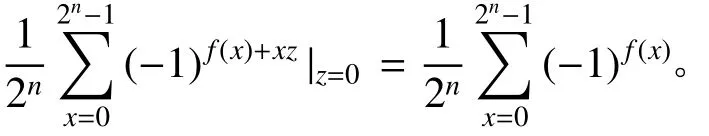
由此可见,当f(x)是常数时,一定可测得|0〉⊗n;当f(x)是平衡函数时,一定不可测得|0〉⊗n。反之,同样可以根据对前n个量子比特的测量去判断f(x)是常数还是平衡函数[9]。
2 Deutsch-Jozsa电路综合算法
2.1 Deutsch-Jozsa电路综合算法
Deutsch-Jozsa算法的Oracle电路如图2所示,在Oracle电路中,第一根量子比特线的输出与输入是一样的;第二根量子比特线的输出值与f(x)的值有关。当f(x)=0,y⊕f(x)=y,即经过黑盒子第二根量子线的输出不变;当f(x)=1,y⊕f(x)=∧y,即经过Oracle电路后第二根量子线翻转[10]。

图2 Oracle电路图Fig.2 Schematic diagram of Oracle circuit
当n=2时,其控制辅助位y翻转的f(x)电路如图3所示。根据生成的f(x)集合将图3中的电路进行级联,即可生成Oracle电路。其部分Python代码如下:


图3 n=2时的 f(x)电路图Fig.3 f(x)circuit for n=2
以n=4为例,随机生成平衡函数f(x)=<0,1,0,1,1,1,0,0,0,0,1,1,1,1,0,0>,构造Deutsch-Jozsa电路如图4所示,其中,t0表示构建电路消耗的时间,t1表示模拟电路消耗的时间,g1表示电路中的总门数,c1表示总层数。同时根据其测量结果验证f(x)是一个平衡函数,也验证了综合算法的正确性[11,12]。
2.2 Deutsch-Jozsa电路综合算法的优化
2.2.1 简化X门
在综合出来的电路中,两个连续的X门相当于一个恒等电路,即可去掉[13]。
部分Python代码如下:

仍然以n=4为例,对图4中的电路进行优化的结果如图5,其中,t2表示优化后模拟电路消耗的时间,g2表示优化后的电路中的总门数,c2表示其电路的总层数。
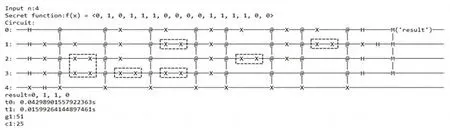
图4 n=4时的Deutsch-Jozsa电路图Fig.4 Deutsch-Jozsa circuit for n=4
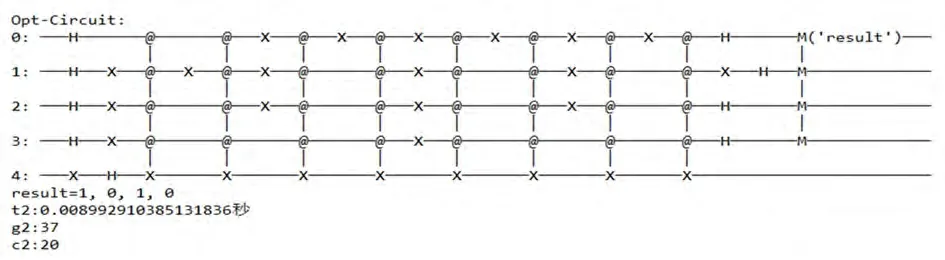
图5 n=4时的电路优化Fig.5 Optimization circuit for n=4
2.2.2 利用X门构造等效电路
当f(x)是一个全是1的常数函数时,构造的电路相当于全0的常数函数加一个X门。以n=3为例,f(x)=<1,1,1,1,1,1,1,1,>是一个常数函数,简化X门后的电路如图6所示。
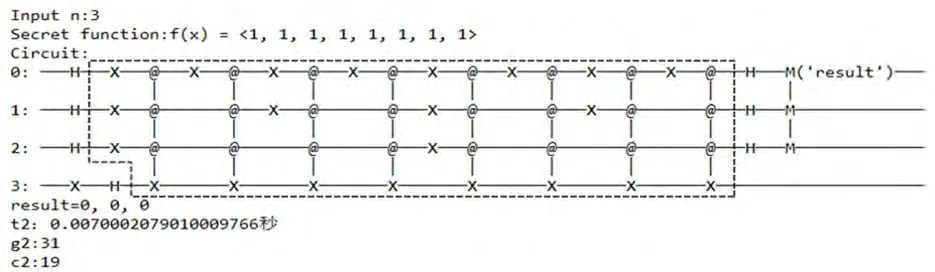
图6 n=3时的Deutsch-Jozsa电路图Fig.6 Deutsch-Jozsa circuit for n=3
Oracle电路使得y⊕f(x)=∧y,其效果等效于添加一个X门,如图7所示。

图7 n=3时的等效电路Fig.7 Equivalent circuit for n=3
3 实验结果及优化情况分析
表1给出了Deutsch-Jozsa电路综合算法在n个量子比特情况下平衡函数的实验结果。其中,t0是利用综合算法构造Deutsch电路消耗的时间,t1、t2分别是优化前后模拟电路时消耗的时间,层数c的含义如图8所示,一个虚线框表示一层,该电路共5层。
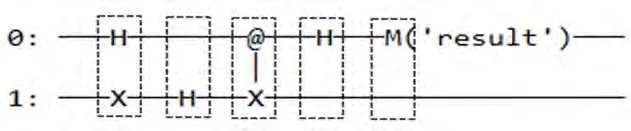
图8 一个简单电路Fig.8 A simple circuit
从表1实验数据可以看出,随着量子位数的增加,构造电路所需要的时间以及电路模拟时间也在增加。当n=1、2时,由于量子门数比较少,其电路优化前后的门数以及层数没有显著的变化。当n≥3时,电路优化以后,其门数的应用、电路的层数以及模拟电路需要的时间成倍数级地减少。n的值越大,优化的效果越明显。
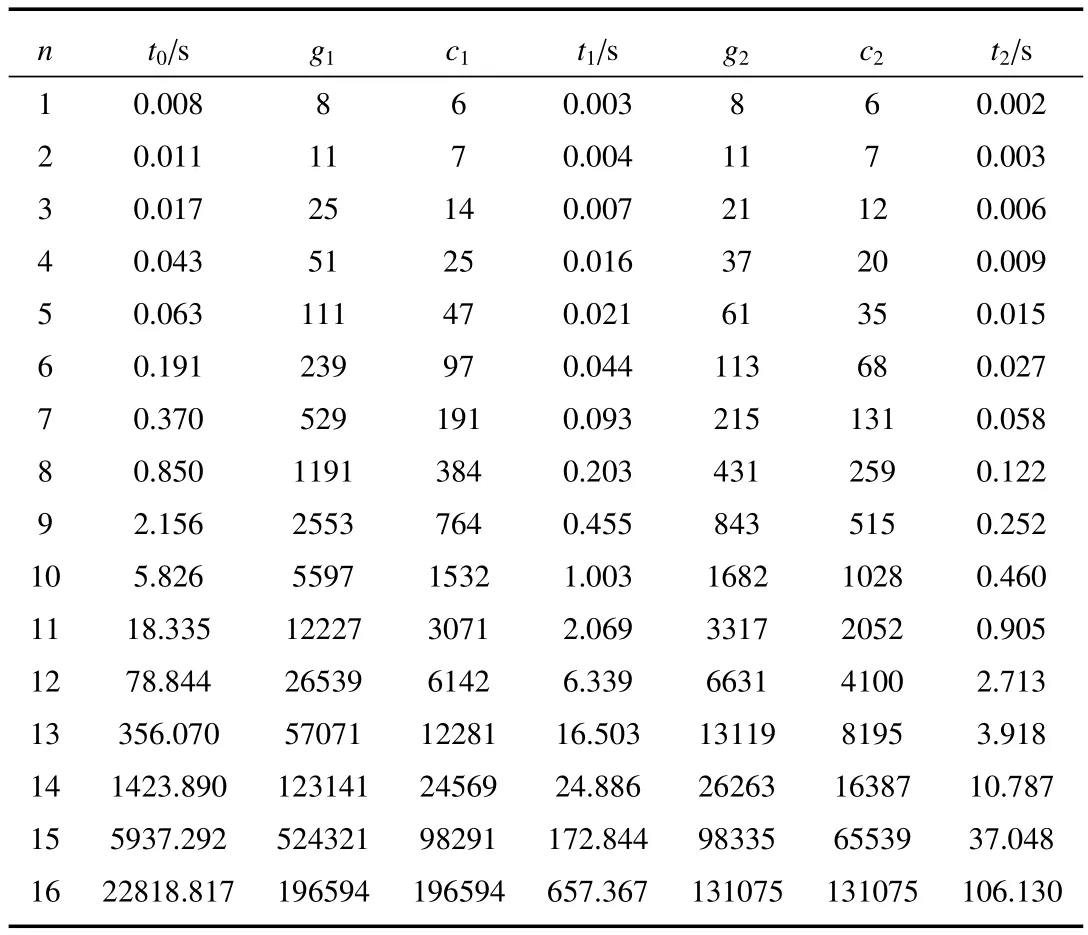
表1 实验结果Table 1 Experimental results
该程序使用ThinkPad E431在Python3.7的环境中运行。当n=17时,该环境已不能正常地构造出电路,因此实验结果对比只展示出n≤16的部分。
4 结论
首次提出利用Google的Cirq框架综合电路算法,具有重要的研究意义。该综合算法可以根据f(x)集合自动构建Deutsch电路并对其进行模拟,优化后的电路相比优化前不仅减少了总门数和总层数,电路模拟的速度有了成倍的提高。Deutsch-Jozsa算法中构建Oracle电路的思路为后续研究Grover量子搜索算法、Shor算法等奠定了基础。

