二维十字型四终端量子点阵列的量子输运

罗国忠

(忻州师范学院物理系,山西 忻州 034000)

0 引言

低维介观体系的电子输运是当前介观物理理论研究的一个重要领域。对于二终端介观体系电子装置的电子输运性质问题,文献[1-4]提出:在自旋简并的情况下,电导G=(2e2/h)T,其中T是透射率。计算T的方法有传输矩阵方法[5-8]、非平衡格林函数等方法[9-14]。

利用低维介观体系基于实空间格点的量子点阵列的传输矩阵方法是获得透射率的重要途径之一。关于处理基于紧束缚模型实空间格点量子点阵列的波透射系数的传输矩阵方法,在文献[14,15]中都曾应用过,此方法适用于多终端系统低维介观体系。文献[8]研究了一维量子点超晶格的电子透射性质。文献[9]研究了一个量子点中电子透射的相变性质。文献[10]研究了连接两个一维电极的散射体的透射振幅相和Frieled相。文献[11]研究了连接电子库的有限长Hubbard量子链的输运。文献[12]研究了连接左右单通道电极的具有两个电子的双量子点电子透射的性质。文献[13]研究了InN量子点中AlGaN/GaN异质结构的负微分电容和能量色散关系。文献[14,15]研究了二维H型和T型多终端量子点阵列的电子输运。本文基于文献[14,15]中的方法,提出了四终端二维十字型量子点阵列体系,并研究其电子传输。

1 一维量子点阵列体系与其电子透射系数传输矩阵方法

一维二终端量子点阵列体系模型是在一维二终端量子点阵列的两端放置理想金属导线来代表电极。用格点来表示一维二终端体系上量子点所在位置,不同的一维介观体系的电极也格点化。电极上格点标记为 -∞,···,-(NL+2),-(NL+1)和 (NR+1),(NR+2),···,+∞,量子点阵列上格点标记为-NL,···,-1,0,1,2,···,NR-1,NR。系统的哈密顿为

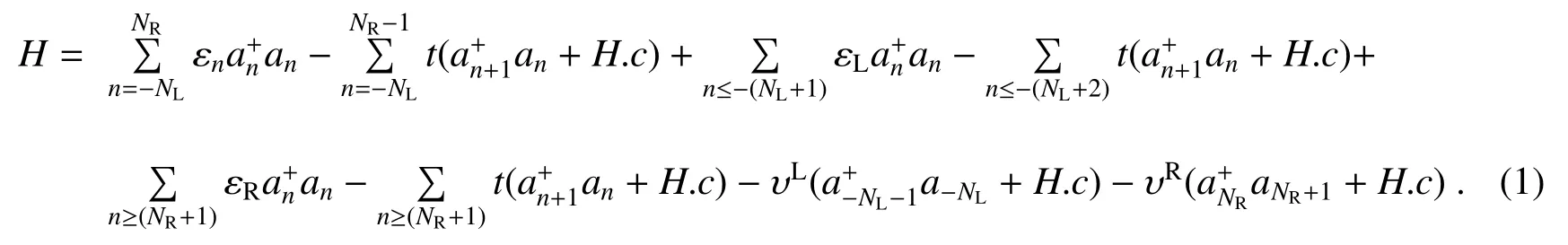
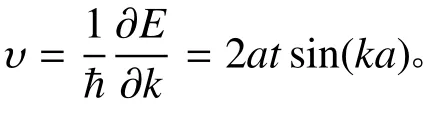
哈密顿的本征方程为

本征解为

哈密顿方程(2)式可写为

所研究系统两个不同理想导线区域的本征函数为

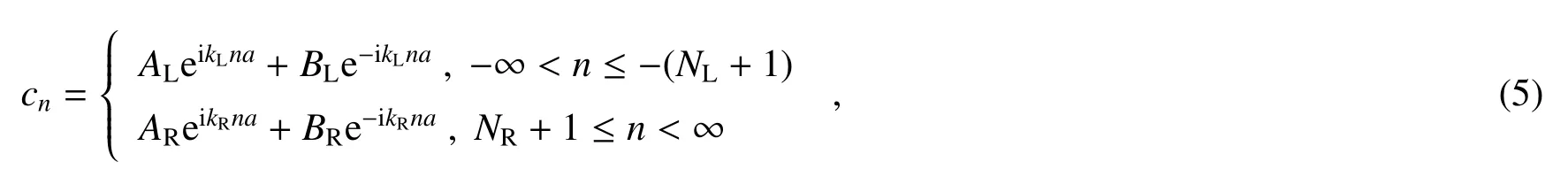
其中不同理想导线的波函数的系数关系为

式中

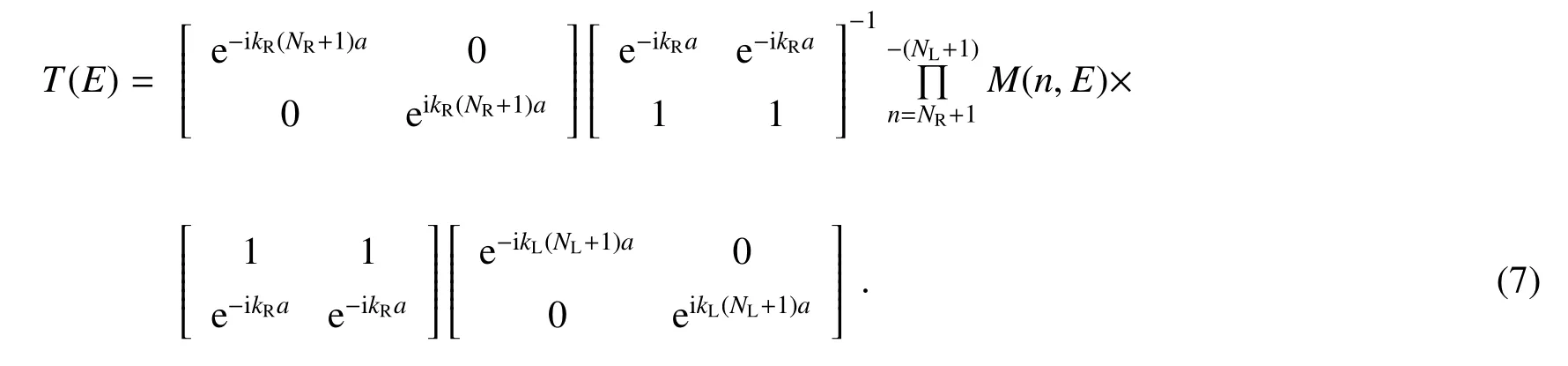
通过散射矩阵法可以得到二终端系统的透射率

式中υR和υL分别是一维量子点阵列左右两端金属导线中电子的速度。

2 十字型四终端量子点阵列的电子输运

由四根导线连接到一个十字型的非均匀区域来构造十字型四终端系统。十字型四终端量子点阵列是通过量子点组成的,可以用一个格点来替代一个量子点,标记为(i,j),其中i,j为整数。如图1所示,量子点阵列的交叉点标记为(0,0),水平量子点阵列的坐标为(-NL,0),(-NL+1,0),···,(NR-1,0),(NR,0);竖直量子点阵列的坐标为 (0,-ND),(0,-ND+1),···,(0,-1)和 (0,1),···,(0,NU-1),(0,NU)。对半无限长的导线分别连接在水平量子点阵列左侧和右侧,坐标为(n,0),其中n≥NR,n≤-NL。系统的左侧量子点位置n=-NL和右侧位置n=NR时跃迁积分分别为tn=νL和tn=νR,NL和NR分别代表水平量子点阵列左侧和右侧的量子点数目。另一对半无限长的导线分别连接在竖直量子点阵列上侧和下侧,坐标为(0,n),且-ND≤n≤NU,其中系统的上侧n=NU和下侧n=-ND时跃迁积分分别为tn=νU和tn=νD,同理NU和ND分别为竖直量子点阵列上侧和下侧的量子点数目。

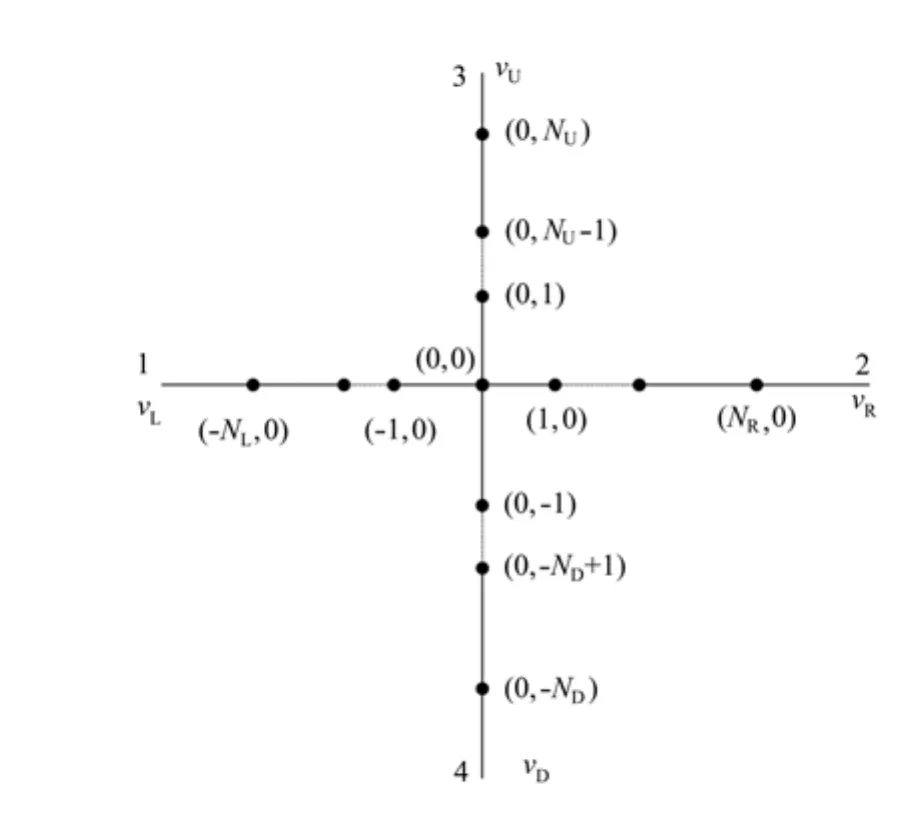
图1 十字形四终端量子点阵列晶格模型Fig.1 Lattice model of a cross-shaped quantum dot array for the four-terminal,quantum-confined system

十字型量子点阵列的哈密顿为

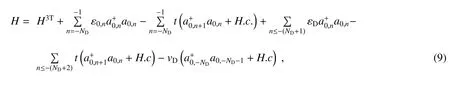
式中

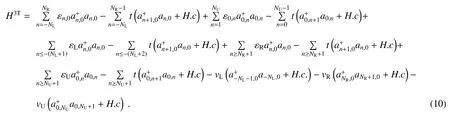
再次考虑从左边注入电子的情况时,其哈密顿的本征解为

不同终端区域的波函数为

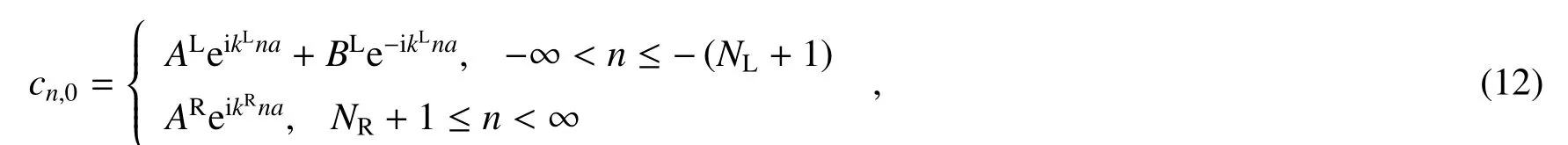
当AL=1,且

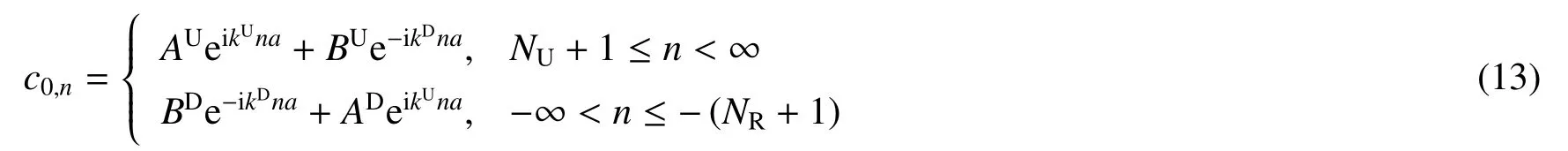
时,首先推导传输公式T21,它被定义为电子从左向右传输的概率。为了推导出T21的公式,需要将四终端系统的薛定谔方程与方程(9)中的哈密顿量转变为二终端系统的薛定谔方程和二终端的哈密顿。

将方程(11)代入原四终端系统的薛定谔方程中,并且通过消去系数的方法来解方程,当n≠0时,可以得出结果为

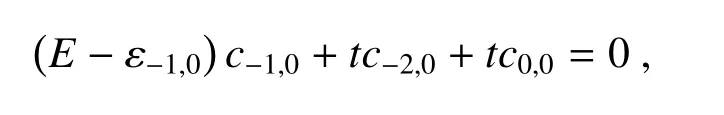
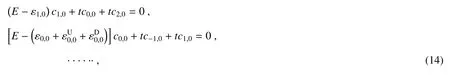
其中

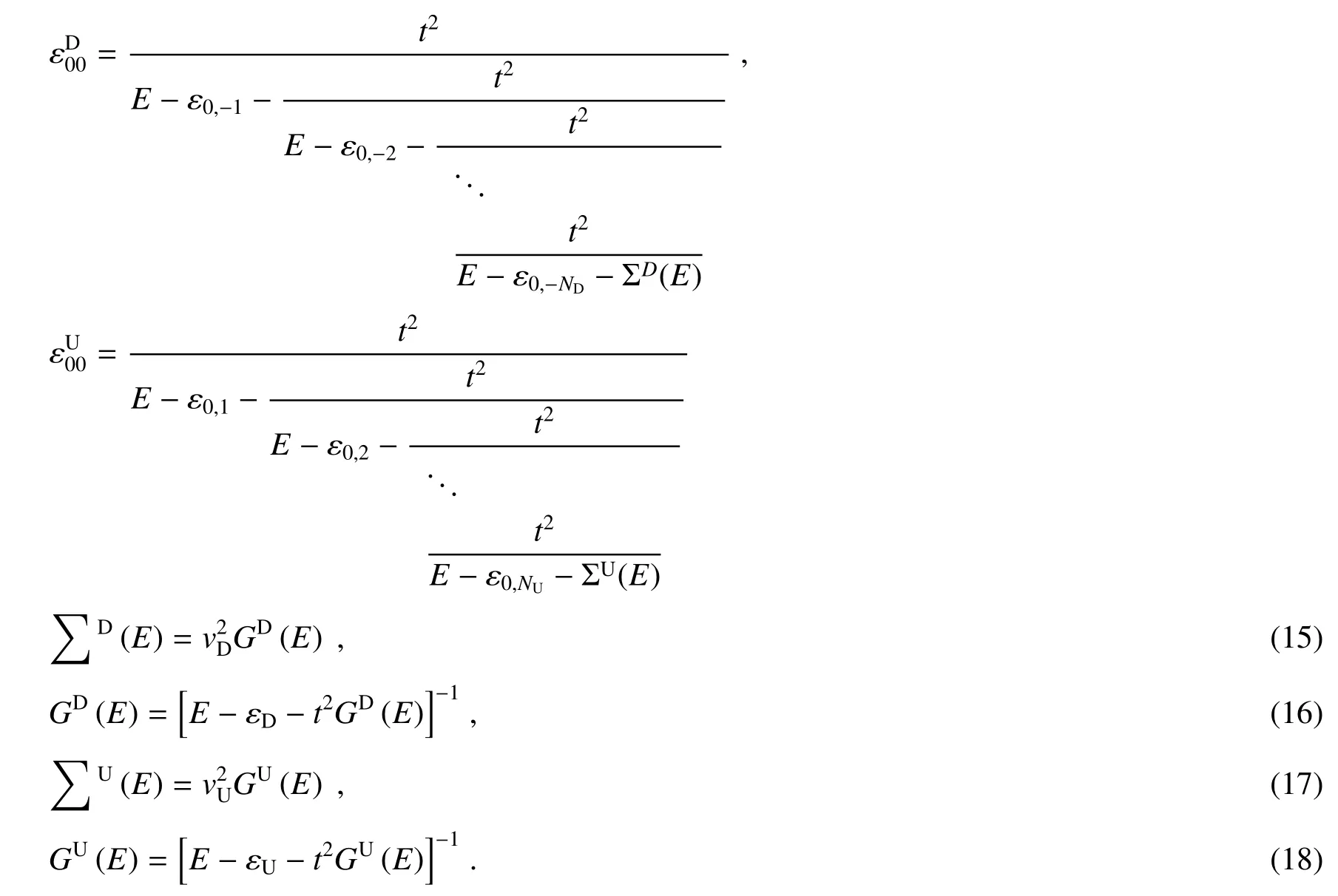
式中∑D(E)是下端自能,GD(E)为下端格林函数,∑U(E)为上端自能,GU(E)为上端格林函数。

对于十字型量子点阵列,取量子点阵列任意一端为输入端,则其余端为输出端。如图1所示,用j=1表示输入端,则i=2,3,4表示该体系的输出端,tij表示从j端入射电子而从i端输出电子的透射率,其中i=1,2,3,4,j=1,2,3,4,并且i≠j。在tij的记号中,i,j=1时代表左侧导线;i,j=2时代表右侧导线;i,j=3时代表上侧导线;i,j=4时代表下侧导线。

反射率为rii,其中i=2,3,4。这些参数可以通过上述方法获得,用于计算透射率t21,t31,t41和反射率rii。此外,得到了四终端系统足够数量的散射参数,在没有磁场并且电流守恒的情况下,利用空间反转对称性t=t,也可以去掉剩余的散射参数。

根据方程组(8)计算四终端系统的透射率t21,即

四终端系统中的透射率t31和透射率t41也可以用类似的方法计算,分别表示为

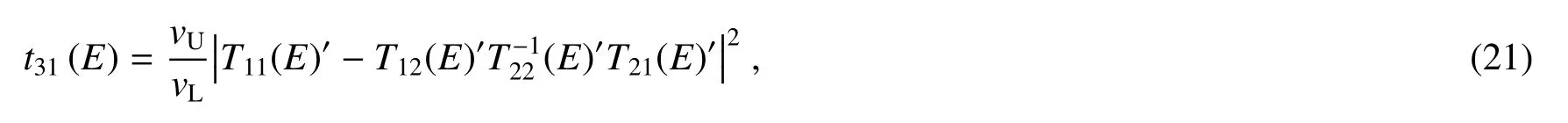
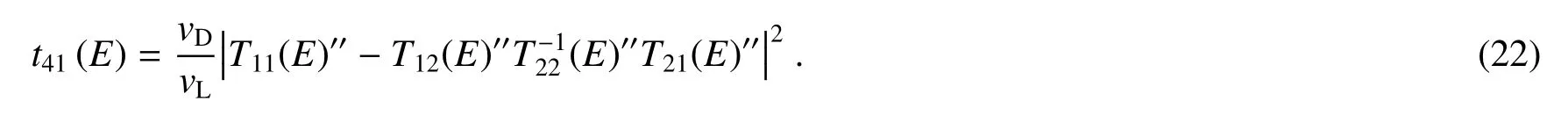
3 数值计算结果与讨论

这里的约束结构是一个有限的十字型非均匀区域。

1)对于一个有限的二维十字型四终端量子点阵列体系,假设相对于原点的左右两侧量子点数相等,上下两侧量子点数也相等,量子点阵列与两侧电极之间的耦合常数υR、υL、υU和υD相同,量子点阵列左右两侧电极中电子的速度υR=υL,Nu=NR=Nl=Nd=6,kL=kR=5,t=100,导线的格点能εn=2t,参数a=90,εL=εR=εU=εD=2t,则理想电极1中的电子透射到电极2时,透射率如图2所示;参数a=50时,从理想电极1中的电子入射再到电极2出射时的透射率如图3所示;参数a=40时,电子从理想电极1→2透射时透射率示意图如图4。

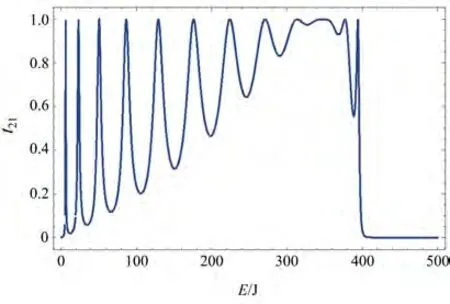
图2 由24个量子点组成的十字形量子点阵列的电极1到电极2的电子透射几率图,其中参数为t=100,a=90,Nu=NR=Nl=Nd=6Fig.2 Transmission probability of electrons from electrode 1 to electrode 2 of a cross-shaped quantum dot array composed of 24 quantum dots,where the parameters are t=100,a=90,Nu=NR=Nl=Nd=6

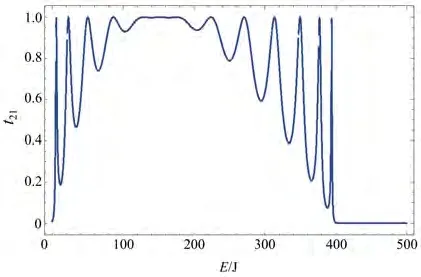
图3 由24个量子点组成的十字形量子点阵列的电极1到电极2的电子透射几率图,其中参数为t=100,a=50,Nu=NR=Nl=Nd=6Fig.3 Transmission probability of electrons from electrode 1 to electrode 2 of a cross-shaped quantum dot array composed of 24 quantum dots,where the parameters are t=100,a=50,Nu=NR=Nl=Nd=6

由图2～4可见,十字型量子点阵列中的1、2电极两端对称时,量子点数随着参数a的减小,在参数t不变的情况下,中间透射率连续为1的平缓处向左移动到能量坐标较小的地方,而透射率t21变成0的能量保持不变。能量在4t时透射率突然迅速变为0。尖峰个数与水平量子点阵列中量子点个数相等。

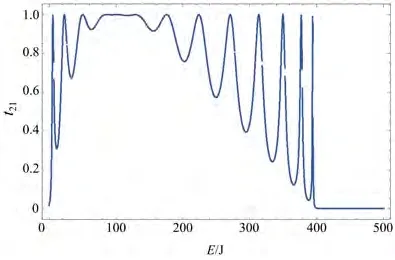
图4 由24个量子点组成的十字形量子点阵列的电极1到电极2的电子透射几率图,其中参数为t=100,a=40,Nu=NR=Nl=Nd=6Fig.4 Transmission probability of electrons from electrode 1 to electrode 2 of a cross-shaped quantum dot array composed of 24 quantum dots,where the parameters are t=100,a=40,Nu=NR=Nl=Nd=6

2)在1)条件的基础上,a=100不变,改变参数t。当t=40时电子从理想电极1→2透射时的透射率如图5所示,t=30时电子从理想电极1→2透射时透射率如图6所示。

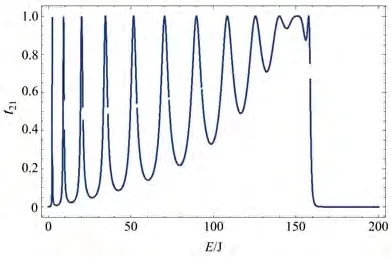
图5 由24个量子点组成的十字形量子点阵列的电极1到电极2的电子透射几率图,其中参数为t=40,a=100,Nu=NR=Nl=Nd=6Fig.5 Transmission probability of electrons from electrode 1 to electrode 2 of a cross-shaped quantum dot array composed of 24 quantum dots,where the parameters are t=40,a=100,Nu=NR=Nl=Nd=6

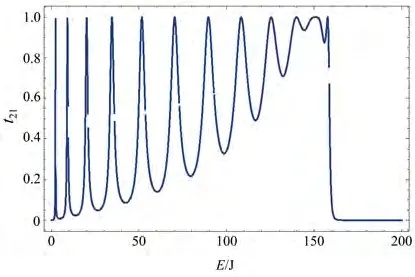
图6 由24个量子点组成的十字形量子点阵列的电极1到电极2的电子透射几率图,其中参数为t=30,a=100,Nu=NR=Nl=Nd=6Fig.6 Transmission probability of electrons from electrode 1 to electrode 2 of a cross-shaped quantum dot array composed of 24 quantum dots,where the parameters are t=30,a=100,Nu=NR=Nl=Nd=6

由图5、6可见十字型量子点阵列中1、2电极端的量子点数对称时,在参数a不变的情况下,跃迁积分t改变,图形形状保持不变,尖峰个数也不变,但随着t的减小,透射率变为0的能量发生改变,且尖峰变密。透射变为0时,能量仍然是在4t值。

1)和2)的研究结果表明随着能量的逐渐增大,大概在4t时,透射率逐渐地变成了0。这表明在系统中,由于量子点单电子隧穿的特性,当能量大于极限值时电子数量过多,达到某个数量就会造成库仑阻塞,所以透射率慢慢地变成了0。

3)对于一个有限的二维十字型四终端且相对于原点上下和左右量子点数不相等的量子体系,假设耦合常数υR、υL、υU和υD仍然相同,理想金属导线中的电子速度仍然相同,取Nu=6,ND=6,NR=2,Nl=3,kL=5,kR=5,a=0.1,t=50,导线的格点能εn=2t,εL=εR=εU=2t,电子从理想电极1透射到电极2时,透射率情况如图7;参数NR=3,Nl=4时,其他参数不变时,电子的透射率如图8所示。

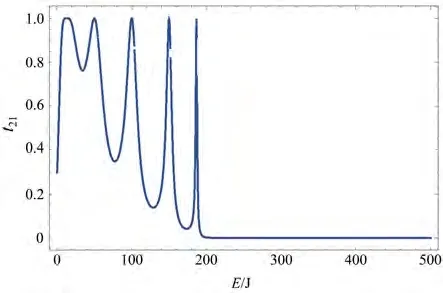
图7 由17个量子点组成的十字形量子点阵列的电极1到电极2的电子透射几率图,其中参数为t=50,a=0.1,Nu=6,Nd=6,NR=2,Nl=3Fig.7 Transmission probability of electrons from electrode 1 to electrode 2 of a cross shaped quantum dot array composed of 17 quantum dots,where the parameter is t=50,a=0.1,Nu=6,Nd=6,NR=2,Nl=3

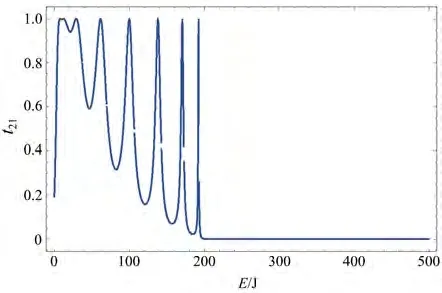
图8 由19个量子点组成的十字形量子点阵列的电极1到电极2的电子透射几率图,其中参数为t=50,a=0.1,NR=3,Nl=4,Nu=6,Nd=6Fig.8 Transmission probability of electrons from electrode 1 to electrode 2 of a cross-shaped quantum dot array composed of 17 quantum dots,where the parameter is t=50,a=0.1,NR=3,Nl=4,Nu=6,Nd=6

由图7、8可见,对于十字型量子限制系统中量子点阵列中的电极1和电极2量子点数目发生改变而其他参数不改变的情况下,在左侧和右侧量子点数目之和为5时,尖峰个数为5;左侧和右侧量子点数目之和为7时,尖峰个数为7,这与T型三终端图形的情况[15]不同,说明图形尖峰个数与量子点个数相同。

4)NR=3,Nl=4,kL=20,kR=20,υR= υL=0.5,导线的格点能 εn=50,εL= εR= εU=2t,参数a=10,电子从理想电极1→2透射时,透射率如图9所示。由图9可见,透射率突变为0时,跃迁积分t越大,入射能量越大。

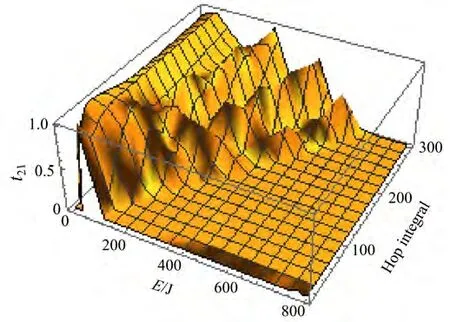
图9 由19个量子点组成的十字形量子点阵列的电极1到电极2的电子透射率随能量和跃迁积分变化图,其中参数为a=10,Nu=6,Nd=6,NR=3,Nl=4Fig.9 Variation of electron transmission probability from electrode 1 to electrode 2 with energy and hop integral in a cross shaped quantum dot array composed of 19 quantum dots,where the parameter is a=10,Nu=6,Nd=6,NR=3,Nl=4

比较文献[14]中二维H型四终端量子点阵列的量子输运和文献[15]中二维T型三终端量子点阵列的量子输运,由前述可知,电子由1透射到2时,其透射率的大小同电子由1透射到其他端时是一样的。对于四终端的H型和十字型,不论跃迁积分如何变化,透射率都几乎不变。对于三终端的T型,不论量子点宽度如何变化,透射率都几乎不变,说明具有空间反转对称的量子点阵列体系其电子透射率与跃迁积分无关,而不具有空间反转对称的量子点阵列体系其电子透射率与量子点宽度无关。

十字型四终端量子点阵列系统中的各种传输概率,即透射率,是电子能量的函数。假设系统中所有的能量是2t,而系统中的能量是系统中所有晶格点上的可裂变能。与二终端系统一样,四终端系统的透射率和反射率表现出了不相同的高峰和低谷。总的来说,四终端、三终端和二终端量子点阵列系统有不同的性质。

4 结论

基于一维二终端介观量子点阵列体系输运的方法,提出了十字型体系。利用传输矩阵方法计算了十字型四终端任意两端中电子从输入端到输出端的透射率。通过透射率的计算比较了透射率与跃迁积分、透射率与左右两侧量子点数目之和的关系,结果表明图像尖峰数与量子点阵列体系中的量子点点数相关。比较了H型四终端、T型三终端和十字型四终端量子点阵列模型的量子输运问题。对于二终端、三终端和四终端系统电子输运性质的理论研究结果,也可以运用到其他复杂的多终端系统中和有限偏置下低维介观体系的量子输运。研究表明,三终端系统和四终端系统也可以与二终端系统一样计算出透射概率,表现出了规则的共振状态。此外,通过有限区域晶格点上的部分状态密度的计算,发现多终端系统的透射光谱和反射光谱的复杂性是因为系统中的受限状态被局限于不同的受限区域,从而影响着不同系统的透射概率和反射概率。