四旋翼飞行器齿轮箱- 支臂组件动态特性分析
赵文辉, 孙晓恒, 张伟东, 郑鹏, 杨帆
(沈阳工业大学 机械工程学院, 辽宁 沈阳 110870)
0 引言
作为旋翼飞行器领域的一个重要分支,油动旋翼飞行器载质量大、航时长[1-2],成为该领域的研究热点。齿轮箱- 支臂组件是将动力从发动机传递到旋翼的关键部件,由于传动芯轴长径比大、支臂横向刚度低以及齿轮箱- 支臂组件受力复杂,在负载工作时的振动会影响飞行器的性能。目前,飞行控制和结构设计是研究的重点[3-7],对飞行器动态特性分析则相对较少。袁朝辉等[8]研究了直升机旋翼电液伺服加载系统的自适应最优解耦控制问题。刘云平等[9]采用Lyapunov指数方法建立了飞行器结构参数与系统运动稳定性之间的量化关系。裴彦华[10]采用传递路径分析方法,对多旋翼无人机进行了拓扑优化。宋彦国等[11]通过改变旋翼变距机构来改善其飞行性能,有效提高了飞行器起飞质量、续航时间等关键性能。潘成龙等[12]研究了飞行器在推力和阻力作用下的动力稳定性。
为提高重载无人机的载重能力,大量采用复合材料管来提供支撑或传动的作用,齿轮箱- 支臂组件处集中载荷产生的动力学问题亟需解决。同时重载无人机的旋翼尺寸较大,导致支臂长径比超过20,长径比过大会直接影响支臂的动态特性。本文以重载油动四旋翼飞行器为对象,对齿轮箱- 支臂组件进行动态特性研究并进行优化。基于Lanczos特征值求解器对组件进行模态分析,通过试验获得组件中心位置的振动加速度数值,结合分析和实验结果确定危险部位并优化传动芯轴长径比。求解各动力学方程,确定动态特性的影响因素和变化规律。
1 齿轮箱- 支臂组件模态分析
1.1 有限元模型的建立
重载油动四旋翼飞行器采用工字型布局。传动路径为:发动机转动→同步带传动→螺旋锥齿轮传动→4个旋翼旋转。4个旋翼转向两两相邻相反,通过改变发动机转速和变距,使飞行器实现上升、转向、悬停等各种动作。飞行器本体总质量260 kg,长4 500 mm,宽4 500 mm,高1 600 mm,最大抗风等级6级,飞行高度3 000 m,最大载重120 kg。飞行器的结构形式如图1所示。

图1 飞行器整体结构Fig.1 Overall structure of aircraft
单发重载四旋翼飞行器是新研发设计的产品,基于快速反应和方便运输的要求,将旋翼部分设计成快速拆装结构。由于齿轮副等内部金属零件的存在,使齿轮箱质量集中,约10 kg。整个装置的动力输出集中于4个旋翼处,旋翼与齿轮箱输出轴相连。传动芯轴(长700 mm)安装于支臂内,主体材质为碳纤维增强树脂复合材料,轴端采用7075铝合金。通过提高连接工艺,铝合金—碳纤维复合材料传动轴的传递扭矩能力达到950 N·m[13]。
齿轮箱支臂组件的支臂端与机架联接,齿轮箱端旋翼轴受垂直向上的升力。当飞行器载重飞行时,受到旋翼激励、空气动力及惯性力的综合作用,导致齿轮箱- 支臂组件产生振动,从而影响飞行稳定性和安全。机身采用铝合金结构件,刚度远高于齿轮箱- 支臂组件,因此本文主要研究齿轮箱- 支臂组件动态特性。组件的简化模型如图2所示,齿轮副采用20CrMnTi材质,传动比为1∶1,主动轮与从动轮齿数均为20,材料属性如表1所示。进行有限元分析,齿轮副网格类型为四面体,其余为六面体,节点总数为23 534,网格总数为13 435,六面体为6 750,四面体为6 685。有限元模型如图3所示。

图2 齿轮箱- 支臂组件简化模型Fig.2 Simplified model of gearbox-arm component

表1 齿轮箱- 支臂组件的材料属性

图3 组件有限元模型Fig.3 Finite element model of component
1.2 外部激励自由振动方程
简化模型划分网格后离散为n个单元,全局坐标系下的运动方程表示为
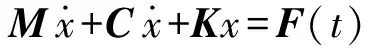
(1)

自由振动时,线性结构的质量矩阵M和刚度矩阵K为常量。线性动力学方程如(2)式所示,特征方程如(3)式所示:

(2)
(3)
式中:ωi为固有角频率,i为阶数;φi为振动模态。
固有角频率ωi与固有频率fi之间的关系如(4)式:
(4)
1.3 组件模态分析
采用Lanczos特征值求解器进行模态求解。传动芯轴为薄壁碳纤维管,弯曲刚度较低,易被激发而引起振动[14-16]。在发动机长时间工作转速为1 500~1 800 r/min前提下,为获取传动芯轴发生大变形时的固有频率和振型,提取组件前18阶固有频率及模态振型如表2和表3所示。

表2 组件前18阶模态频率Tab.2 The first 18 order modal frequencies of component

表3 组件的前18阶模态振型
第1、第2阶共振频率约54 Hz,表现为旋翼带动齿轮箱上下振动,使支臂和传动芯轴发生变形。3~5阶主要为从动轴上零件的振动导致齿轮箱前后方向振动。前6阶振幅较大,模态频率由54.614 Hz增加至352.20 Hz。6~16阶、18阶主要表现为齿轮箱内部各零件的不规则振动。第17阶共振频率为1 014.9 Hz(接近1 500 r/min时啮合频率的2倍频),传动芯轴明显变形。结合激励频率,17阶模态极有可能被激发,引起结构的共振。
2 振动试验与长径比优化
2.1 振动试验条件
为验证有限元仿真的准确性并明确共振频率,使传动芯轴输入端与VMC-850P加工中心的输出轴相连,对齿轮箱- 支臂组件进行振动测试试验。选用压电式加速度传感器,测试组件中心位置在不同转速下的振动情况,如图4所示。

图4 振动试验Fig.4 Vibration test
2.2 振动试验结果分析
对采集的时域数据通过快速傅里叶变换转化成频域曲线,可以看到信号在不同频率下的类型和具体幅值[17-19]。图5为组件在不同转速下的振动加速度a时域和频域曲线。
输入转速1 000 r/min时基频为16.7 Hz。由图5(b)可知,振幅最大处对应频率为1 000 Hz,为螺旋锥齿轮副啮合频率(16.7×20齿=334 Hz)的3倍频,对应固有频率为第17阶模态,表现为传动芯轴的变形。对比图5(b)、图5(f)可知,1 000 Hz对应的振幅远大于啮合频率对应的振幅,并且不受激励频率影响,则该频率及其边频带为组件的固有频率。而为了减轻质量,传动芯轴采用2 mm厚复合材料碳纤维管,长径比达到20,属于高速柔性转子,横向刚度较低。
输入转速500 r/min、1 500 r/min,啮合频率分别为166.7 Hz、500.0 Hz。1 000 Hz是其6倍频和2倍频,振幅与1 000 r/min的幅值(0.12 mm/s2)相差不大。由于细长空心管的模态容易被激发,也有发生共振的危险。
输入转速2 000 r/min时,啮合频率为 666.7 Hz。1 000 Hz为啮合频率的1.5倍,边频比啮合频率高,在啮合频率的左侧边频带大于啮合频率和其右边频带,已经过了共振带。输入转速2 500 r/min时,时域波形比较复杂,频谱图中背景噪声大于信号频率特征。由时域、频域曲线,振动加速度在1 000 Hz处接近3 mm/s2,对应第17阶固有频率,表现为传动芯轴变形,因此振动影响最大的部件为传动芯轴。
2.3 芯轴长径比优化
传动芯轴总长700 mm,当长径比约为20时振动特性不佳,对应的模态频率接近1 000 Hz。当外界激振频率接近模态频率的倍频或者分倍频时,容易使结构发生振动。
传动芯轴的初始设计外径为35 mm,间隔5 mm依次增大传动芯轴外径,对组件进行模态分析。发生最大变形时的模态频率与外径的关系如图6所示。
选取传动芯轴直径的原则是在控制自身质量的前提下,使组件的自身模态频率避开激励频率±10%的范围。表4、图7所示为传动芯轴外径50 mm时的模态分析结果(变形缩放系数为73.27)。
根据模态分析结果,当增加传动芯轴外径至50 mm时,第18阶模态的最大变形为1.022 mm,模态频率为1 137.4 Hz,为外界激励2 000 r/min时齿轮啮合频率的1.7倍频,避开了外界激振频率的倍频和分倍频,有效地避免了共振的发生。
3 基于动力学方程的斜支撑角度优化
芯轴长径比优化后,避免了齿轮箱支臂组件自身的共振,但是组件仍是整机刚性的最薄弱部分。为此建立描述系统响应变化规律的运动方程,以真实反映齿轮箱- 支臂组件在整机中的动态特性,并对支撑进行优化。本文采用Runge-Kutta法MATLAB自编软件求解组件系统在不同条件下的振动加速度。支臂采用碳纤维管,相对齿轮箱而言是一个刚度低的部件。齿轮箱- 支臂组件的质量主要集中在齿轮箱处,而旋翼所受升力也集中作用于齿轮箱,因此将齿轮箱- 支臂组件简化为单自由度系统,分析其主要动态特性。沿支臂轴向设为x轴方向,齿轮箱向机架方向为正;从动齿轮轴为y轴方向,向上为正;根据笛卡尔坐标系确定z轴方向,组件的动力学方程[20]可表示为

图5 不同转速下振动加速度时域、频域曲线Fig.5 Time-domain and frequency-domain curves of component vibration acceleration at different rotating speeds

图6 模态频率随传动芯轴外径变化曲线Fig.6 Variation curve of modal frequency with outer diameter of mandrel

表4 传动芯轴外径50 mm时组件的模态频率

图7 传动芯轴外径为50 mm时的模态振型Fig.7 Vibration modes of the components (the outer diameter of entire mandrel=50 mm)

(5)

轴(管)类零件的弯曲刚度kb和拉伸刚度ks按(6)式和(7)式计算得到:
(6)
(7)
式中:E为材料的弹性模量;l为零件长度;I为惯性矩,
(8)
D、d分别为管类零件的外径和内径;S为轴类零件的截面积,
(9)
3.1 无支撑工况动力学分析
齿轮箱- 支臂组件无支撑、无升力时的装配形式与受力关系如图8所示。图8中,F为螺旋桨对组件的作用力,G为齿轮箱重力,g为重力加速度,n为转速(r/min)。与振动试验和实际情况相一致,在距离齿轮箱体460 mm处加固定约束,齿轮箱重力G垂直向下。求解齿轮箱顶部中心位置处的振动加速度值。

图8 无支撑作用下的组件简图Fig.8 Sketch of component without supporting
组件等效质量m为8.776 kg,总刚度为4.405×106N/m,总阻尼为2 114 N·s/m。采用Runge-Kutta法MATLAB程序对(5)式的求解结果如图9、图10所示。图10中,ay,max为y轴方向振动加速度幅值,ωn为固有频率(rad/s)。

图9 不同转速下的加速度- 时间曲线Fig.9 Time vs. acceleration at different rotating speeds

图10 无支撑作用下y轴方向振动加速度- 转速幅值曲线Fig.10 Variation curve of y-direction vibration acceleration amplitude with rotating speed without supporting
3.2 底部支撑工况动力学分析
如图11所示,机架固定在距离齿轮箱700 mm位置处,在齿轮箱底部与机架支架之间添加夹角为α的斜支撑,支撑杆产生沿杆方向的轴向力,有助于降低系统y轴方向的振动。

图11 加底部支撑后的组件简图Fig.11 Sketch of component with bottom support
此时组件等效质量m为8.848 kg,y轴方向总刚度为2.644×106N/m,固有频率为546.65 rad/s,总阻尼为1 644.5 N·s/m;z轴方向总刚度为7.296×105N/m,固有频率为287.16 rad/s,总阻尼为863.86 N·s/m。分别代入MATLAB程序对(5)式求解,得到y轴、z轴方向振动加速度幅值随转速的变化规律如图12所示。图12中az,max为z轴方向振动加速度幅值。

图12 有底部支撑时振动加速度- 转速幅值曲线Fig.12 Rotating speed vs. vibration acceleration amplitude with bottom support
3.3 斜支撑工况动力学分析
在齿轮箱侧面和机架之间添加一个斜支撑杆,如图13所示。图13中,α、β分别为斜支撑杆与Oxy平面、Oyz平面之间的夹角。取α的大小近似为35.5°,β的大小近似为53.5°,斜支撑杆与Oxz平面夹角γ′的取值范围为0~11°。

图13 加斜支撑后的组件简图Fig.13 Sketch of component after adding a diagonal support

图14 系统刚度、阻尼以及振动加速度幅值随斜支撑角度变化曲线Fig.14 Variation of system stiffness,damping and vibration acceleration amplitude with inclined support angle
通过计算以及相关程序求得,此时组件等效质量为8.925 kg,y轴、z轴方向的总刚度k、总阻尼c、振动加速度幅值aymax随斜支撑角度变化规律如图14、图15所示。

图15 不同角度下转速- 加速度幅值曲线Fig.15 Variation curve of acceleration amplitude with rotating speed at different angles
表5、表6分别为不同角度和转速下y轴方向、z轴方向振动加速度的变化率。

表5 不同角度、转速下y轴方向振动加速度的变化率Tab.5 Rates of change of y-direction vibrationacceleration at different angles anddifferent speeds
采用Runge-Kutta法编程求解组件动力学方程,得到振动加速度随转速和斜支撑杆角度的变化规律。振动加速度幅值随转速的增加先增大后减小,激励频率与固有频率相等时达到最大。在加斜支撑的情况下,支撑杆与Oxz平面的夹角由0°增加至11°时,y轴方向振动加速度的值显著减小(接近30%),z轴方向振动加速度的值变化不明显(增加约3.7%)。

表6 不同角度、转速下z轴方向振动加速度的变化规律Tab.6 Rates of change of z-direction vibrationacceleration at different angles anddifferent speeds
4 结论
本文基于有限元法和求解动力学方程的方式,分析了油动四旋翼飞行器的齿轮箱- 支臂组件的动态特性,并通过试验验证了上述分析结果的准确性,优化了传动芯轴长径比和斜支撑的角度。得出主要结论如下:
1) 在重载油动四旋翼飞行器整体受力分析的基础上,对齿轮箱- 支臂组件进行了模态分析,提取了前18阶模态频率和振型,用振动测试仪测试了组件在不同输入转数下的振动加速度。
2) 结合采集的数据和模态分析结果,分析了振动与固有频率、激振频率之间的规律,确定了传动芯轴(长径比21.21,模态频率1 014.9 Hz)容易引起结构共振。优化传动芯轴的长径比,当传动芯轴外径达到50 mm(长径比为14)时,模态频率为1 137.4 Hz,避开了激励频率的倍频和分倍频。
3) 基于Runge-Kutta法编程求解了齿轮箱- 支臂组件的振动加速度。随转速的增大,振动加速度幅值先增大后减小,在激励频率与固有频率相等时达到最大。当α取值35.5°、β取值53.5°时,在允许的角度范围内,当取值为由0°增加至11°时,其y轴方向的振动加速度变化显著,减小接近30%;z轴方向振动加速度则增加近3.7%,变化不明显。

