环形燃烧室中凹腔对C2H4/Air旋转爆轰流场影响的数值模拟
孟豪龙, 翁春生, 武郁文, 郑权, 肖强, 王放, 白桥栋
(南京理工大学 瞬态物理国家重点实验室, 江苏 南京 210094)
0 引言
与爆燃燃烧相比,爆轰燃烧具有更高的热循环效率和更快的热释放速率[1]。近年来,诸多学者开始利用爆轰推进技术来提高航空航天发动机的推进性能。在航天推进领域,基于爆轰燃烧的发动机主要有3种:脉冲爆轰发动机[2]、斜爆轰发动机[3]以及旋转爆轰发动机[4](RDE)。由于RDE只需一次起爆即可实现推进剂的连续爆轰燃烧,且结构简单、应用广泛、推力稳定,并具有推力矢量调节的能力[4-6],引起了国内外研究机构的广泛关注。RDE利用一个或多个旋转爆轰波( RDW)在燃烧室头部连续旋转传播,燃烧产物从出口高速排出,进而产生推力。作为一种新型推进动力装置,旋转爆轰燃烧室(RDC)构型尚未统一,目前主要有同轴圆环形[2, 4, 6]、无内柱圆筒形[7]和圆盘形[8]3种构型。
Kindracki等[9]和Kindracki[10]在不同燃烧室构型和喷注条件下通过实验研究了RDW的传播特性,分析了爆轰波传播速度和喷注条件之间的关系。刘世杰等[11-12]、Lin等[13]对以H2/Air为推进剂的RDW传播模态进行了实验研究,通过改变工质的工况和燃烧室部分结构参数,分析了它们对爆轰波传播模态的影响。Wang等[14-15]通过高速摄影观测到燃烧室内存在多个爆轰波传播的现象,并认为在RDC内同时存在爆轰燃烧和爆燃燃烧。Fabian等[16]通过OH*化学发光成像研究了RDC内的燃烧现象,将RDC内的爆燃分为寄生燃烧和共生燃烧,其中爆轰波前新鲜燃料的提前点火为寄生燃烧,发现寄生燃烧会导致爆轰波传播速度降低。Peng等[17]通过实验研究了RDC内爆轰与爆燃的竞争关系,并建议应尽可能缩短燃料的起爆距离以降低寄生燃烧的影响。Zhao等[18]对二维RDC模型进行了数值模拟研究,发现在预混模式中,至少70%的H2燃料以爆轰的形式被消耗。
由于以H2/Air为推进剂的RDC实现难度相对较小,目前大量关于RDW的数值模拟和实验研究主要以H2为燃料。液态碳氢燃料由于活性低、雾化掺混困难等诸多限制,通常需要额外添加O2或其他高反应活性的燃料以实现爆轰波的稳定自持[19]。但不可否认的是,在工程应用领域液态碳氢燃料的安全性和廉价性使它成为理想的RDC燃料[20]。C2H4作为实验中煤油热裂解产物的主要成分,研究其基本的旋转爆轰传播特性也是非常有意义的。Wilhite等[21]使用C2H4/Air进行了一系列RDC实验研究,证实了以C2H4/Air为燃料RDC的可行性,并分析了不同参数对发动机性能的影响。George等[22]使用C2H4/Air在环形RDC内进行了实验研究,爆轰波传播速度仅为850 m/s,速度亏损接近50%。Pal等[23]进行了非预混C2H4/Air高度保真的RDC数值模拟研究,RDW表现出严重的不稳定性,波速接近理想Chapman-Jouguet(C-J)速度的一半。
以上分析表明,目前碳氢燃料RDC仍然存在起爆难度大和爆轰特性差等诸多问题需要解决。在超燃冲压发动机领域,于超音速气流中点火和稳定火焰通常是十分困难的。凹腔广泛地用以提高点火特性和火焰稳定性[24]。数值模拟的研究也发现凹腔内的低速高温回流区可以有效地改善燃料与氧化剂的掺混效果[25]。受此启发,Peng等[26-27]和Liu等[28]将环形RDC与凹腔结构相结合,首次提出了凹腔基环形RDC构型,并在此基础上开展了一系列实验研究,系统地研究了凹腔深度、凹腔位置等因素对C2H4/Air的RDW传播特性的影响。实验证实了凹腔的存在有助于碳氢燃料RDW的实现和自持传播,发现了在凹腔内存在回流区,回流区内的燃料主要以等压燃烧的形式释放热量,另外发现凹腔的存在可以有效地扩宽RDC的工作范围。
通过在同轴圆环形RDC内配置凹腔可以显著提高碳氢燃料RDC的可行性,进而发挥其能量密度高、便于存储等优势。但是,针对其开展的研究还相对较少,主要是国防科技大学[26-28]展开的相关实验研究。但是对于充分认识凹腔对同轴环形RDC的影响是不够的,深入的数值模拟研究通常作为辅助手段,用于揭示RDC的流场结构以及RDW的传播机理。
本文使用在开源CFD软件开源的场运算和处理(OpenFOAM)平台上修改的基于有限体积法的求解器rhoReactingCentralFoam[29],以C2H4为燃料、Air为氧化剂,开展同轴圆环形和凹腔基环形两种构型RDC的数值模拟。对比两种RDC流场的主要特征,研究凹腔对RDW传播特性的影响,分析凹腔对燃料燃烧属性的影响。本文研究对于优化旋转爆轰燃烧室构型以及丰富凹腔对旋转爆轰的作用机理具有一定的指导意义。
1 数值方法
1.1 计算方法
使用rhoReactingCentralFoam求解器进行三维RDC数值模拟研究,该求解器是在开源计算流体力学软件OpenFOAM 7.0的框架内开发的。其求解了三维可压缩反应流动的Navier-Stokes(N-S)方程,控制方程如下:
(1)
(2)
(3)

(4)
p=ρRT
(5)

(6)
μ为由Sutherland定律计算得到的黏度,
(7)
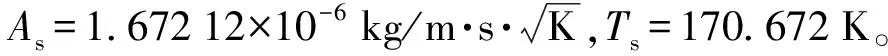
(1)式~(4)式通过有限体积法离散,通过将最大CFL数设置为0.1来调整时间步长。对流项的离散采用Kurganov等[30]的2阶Godunov型中心迎风格式。使用C2H4/Air两步化学反应机理[31]生成化学反应源项,并采用欧拉隐式方法求解。C2H4/Air两步化学反应机理包含6种组分(C2H4, O2, CO, H2O, CO2, N2),由两个反应组成,分别对应C2H4氧化成CO和H2O以及CO-CO2反应平衡。化学反应如下:
C2H4+2O2⟹2CO+2H2O
(8)
CO+0.5O2⟺CO2
(9)
(8)式的反应速率以及可逆反应(9)式的正向和反向反应速率分别为
(10)

(11)
(12)
式中:A为指前因子,下标分别表示C2H4氧化反应以及CO-CO2正向和反向反应;Ea,C2H4为C2H4氧化反应的反应活化能;Ea,CO-CO2,f为CO-CO2正向反应的反应活化能;Ea,CO-CO2,r为CO-CO2反向反应的反应活化能;nO2,C2H4为C2H4氧化反应中O2的反应指数;nO2,CO-CO2,f为CO-CO2正向反应中O2的反应指数。表1所示为活化能和反应指数的值。
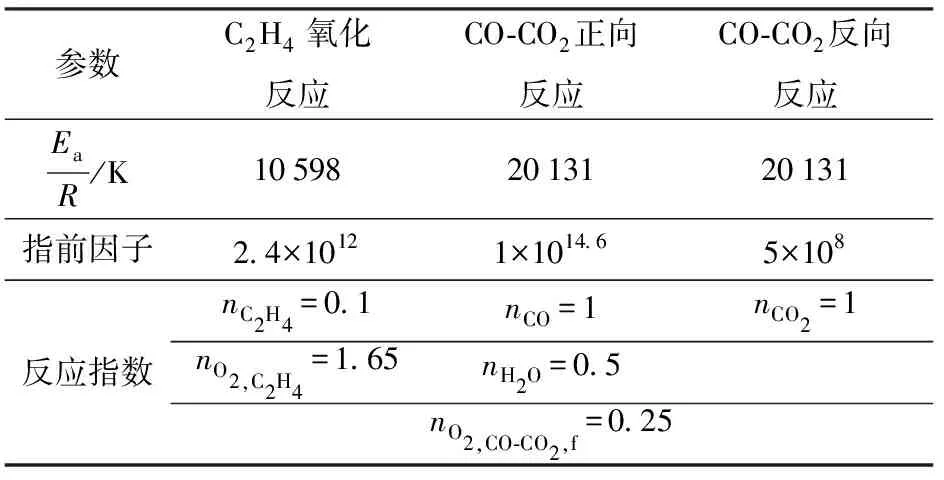
表1 两步C2H4/Air反应机理的活化能、指前因子和反应指数Tab.1 Activation energy, pre-exponential factor andreaction exponents for two-step C2H4/Airreaction mechanism
目前考虑湍流影响的RDC数值模拟研究还相对较少,Cocks等[32]使用大涡模拟方法对非预混喷注的RDC进行了数值模拟研究,但没有分析湍流作用对RDC流场的影响。Zhang等[33]对比了使用N-S方程模拟三维RDC流场时有无湍流模型的区别,采用了简化Baldwin-Lomax湍流模型。结果表明有无湍流模型得到的流场压力分布保持一致,不考虑湍流模型的N-S方程已经满足捕捉旋转爆轰流场特征的需求。另外,刘朋欣等[34]也对比分析了使用不同的计算方法(N-S方程、雷诺平均N-S方法和改进的延迟分离涡模拟方法)对三维RDC流场的影响,认为当RDC入口采用预混喷注假设时,湍流模型对发动机的推力和爆轰波的传播速度影响不大。考虑到本文采用的预混喷注条件,在计算过程中没有使用湍流模型。
1.2 计算模型和边界条件
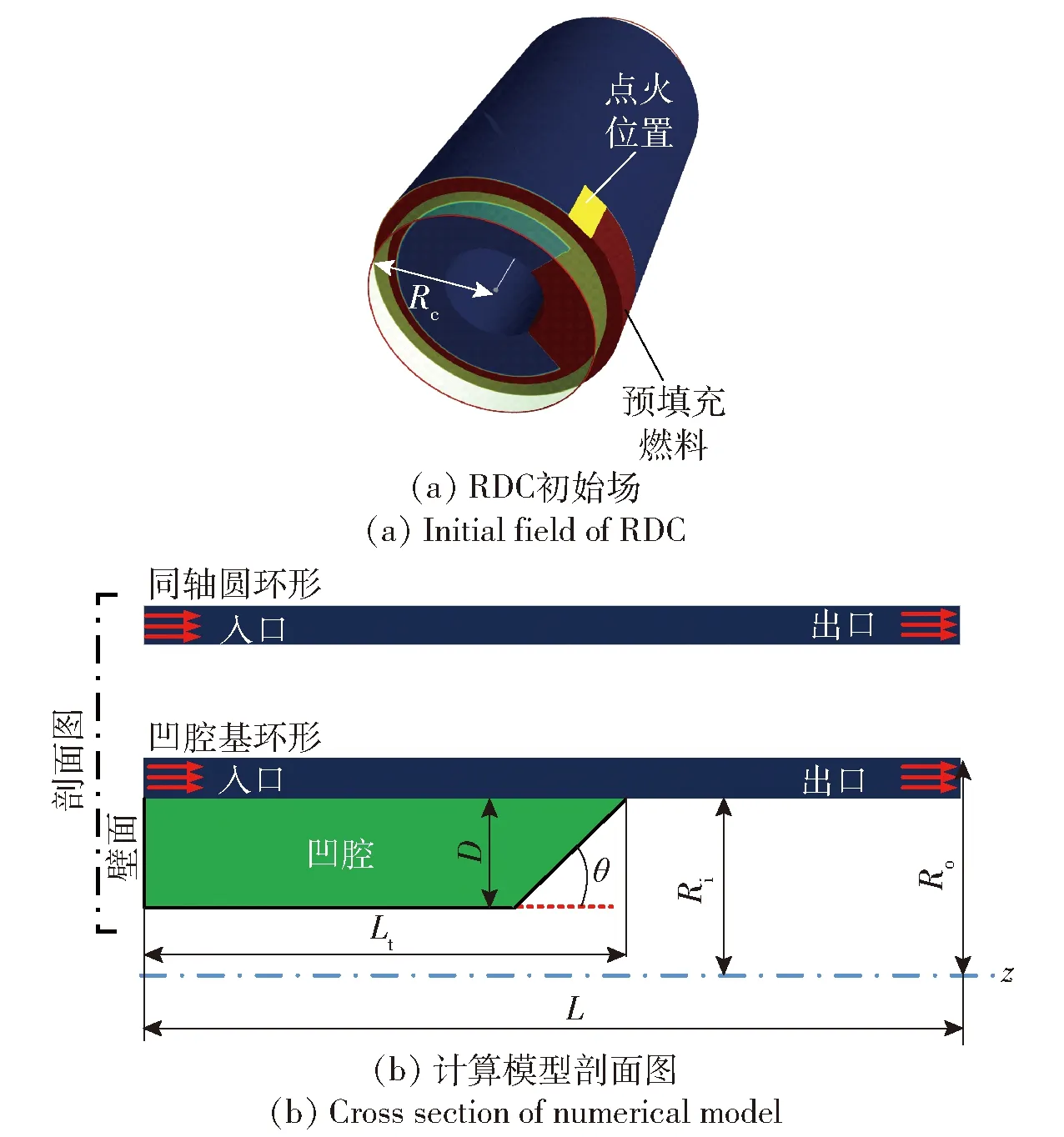
图1 RDC计算模型示意图Fig.1 Numerical model of RDC
如图1所示,对于同轴圆环RDC构型,燃烧室内径Ri=20 mm,外径Ro=25 mm,中心半径Rc=22.5 mm。轴向方向为z轴方向,轴向长度L=80 mm,入口端面处z=0 mm,出口端面处z=80 mm。凹腔基环形RDC模型的外径和轴向长度与同轴圆环RDC保持一致,并在其基础上配置了凹腔结构。两种构型RDC的燃料入口位置和尺寸相同,其中凹腔基环形RDC的燃料入口内侧,即凹腔的上游顶端为壁面,没有燃料流入。凹腔段总长度Lt=50 mm,凹腔深度D=10 mm,凹腔末尾收缩角度θ=45°。爆轰波在燃烧室中沿圆周方向循环传播,预混当量比为1的C2H4/Air混合物从燃烧室头部入口喷入,燃烧产物从出口排出。初始时刻,填充高度为10 mm,距离等于1/4燃烧室周长的预混可燃气。温度为300 K,填充压力0.1 MPa。点火位置为一个高温高压区域,温度2 500 K,压力1.5 MPa。
入口为填充边界,采用一维等熵入流边界条件[18],不考虑气流从集气腔进入燃烧室的流动损失。设pt为填充总压,Tt为总温,pi、Ti、w为燃烧室入口边界上的压力、温度以及轴向速度,pcr为声速填充条件下的临界压力,γ为混合气体的比热比。填充边界分3种情况:
1)当p≥pt时,此时预混燃料不能进入燃烧室,按固壁边界处理;
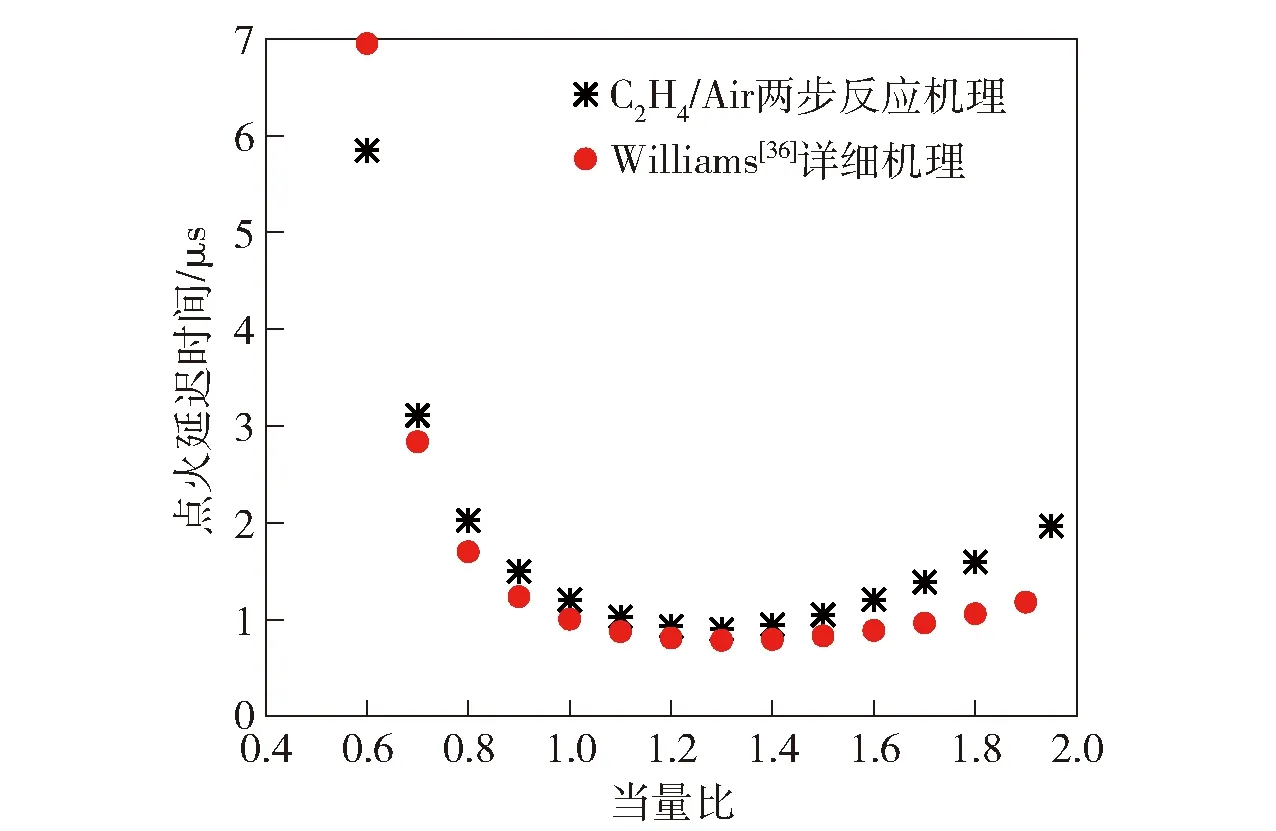
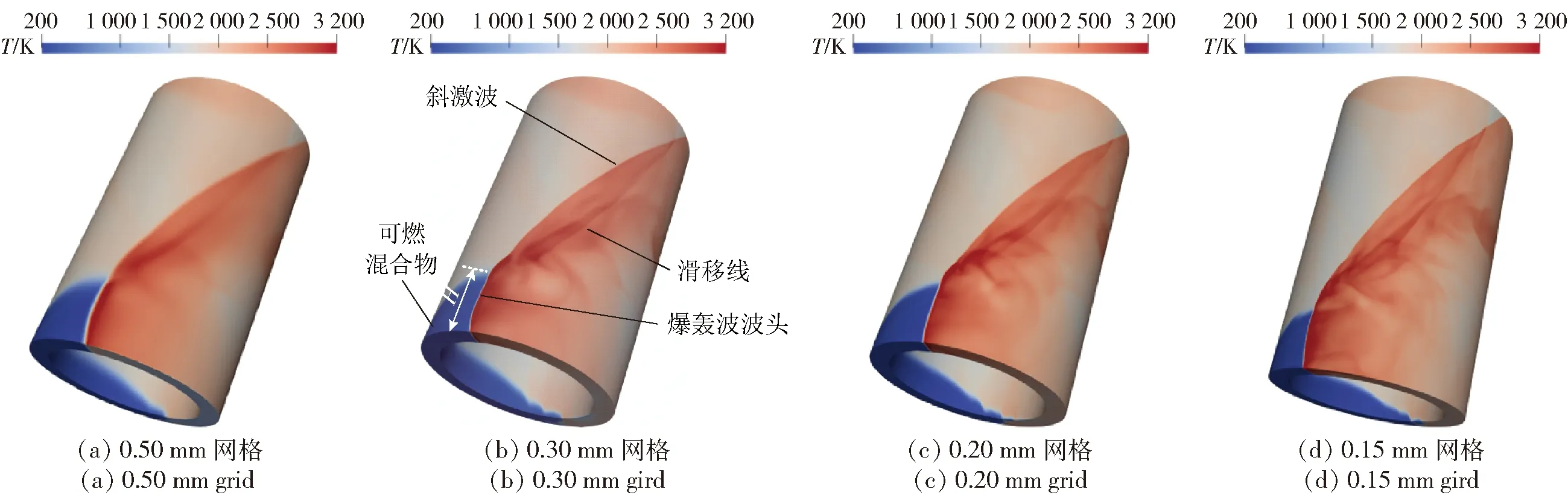
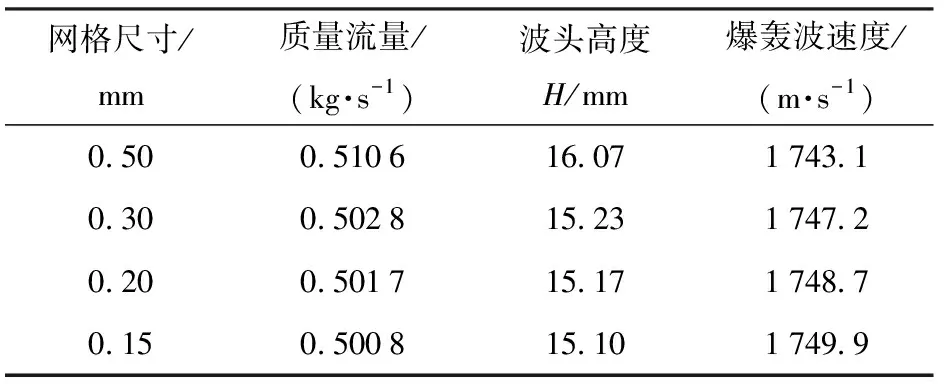
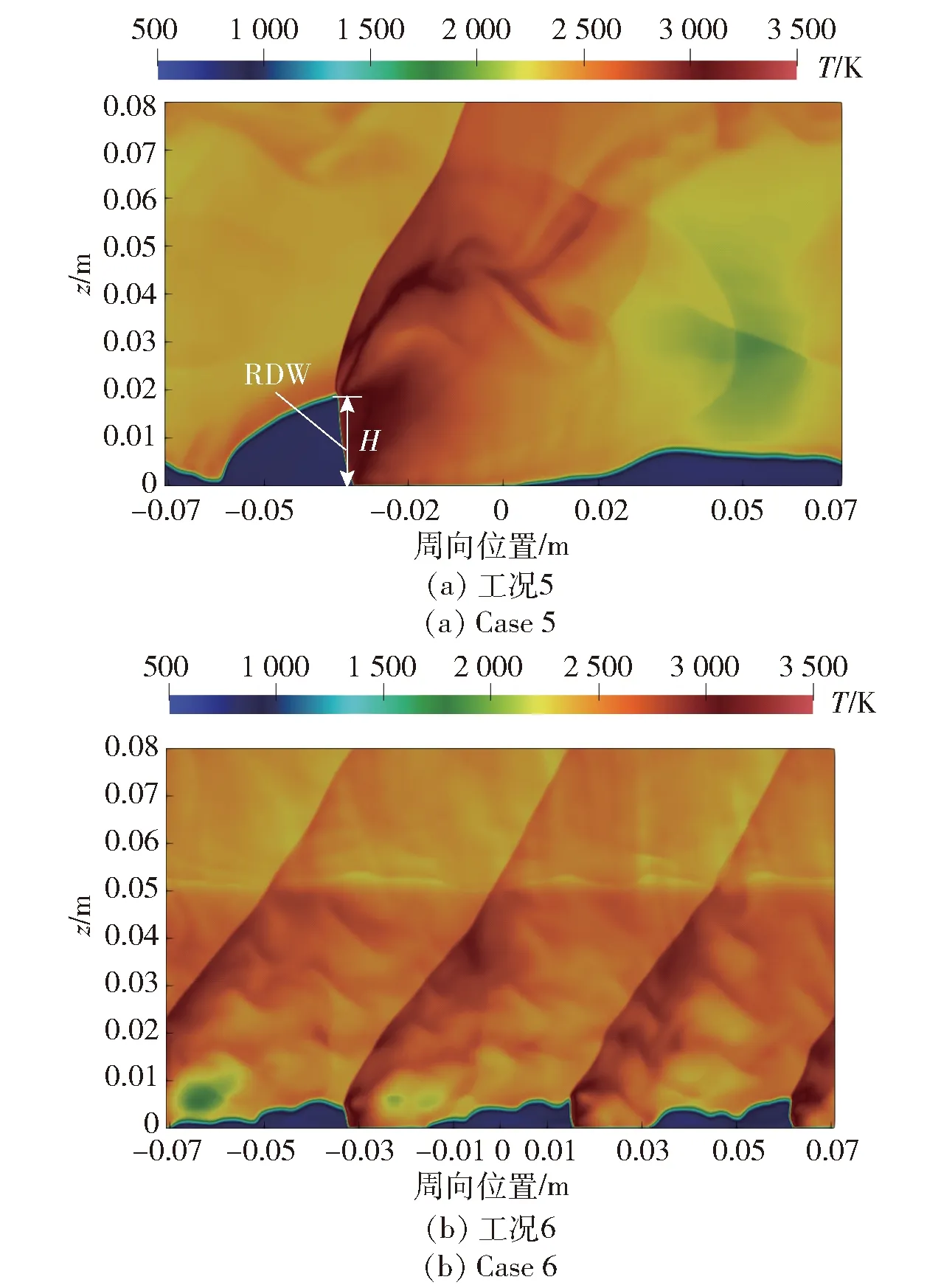
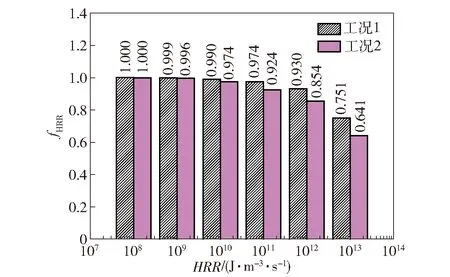
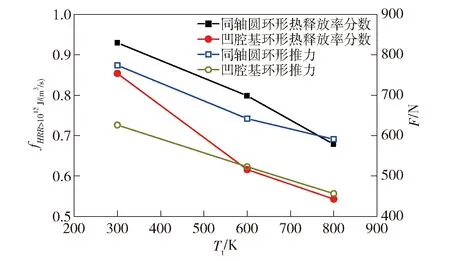
2)当pcr (13) (14) (15) 3)当p pi=pcr (16) (17) (18) 出口为排气边界,使用无反射自由边界条件,分为两种情况:当出口速度为超声速时,根据特征线理论,下游流动不会对上游流动产生影响,令出口压力等于紧邻出口边界处网格上的值。当出口速度为亚声速时,出口压力等于环境压力p∞(0.1 MPa)。壁面采用滑移边界条件。 1.3.1 两步化学反应模型 基于Cantera化学动力学软件和Lawson等[35]的SDtoolbox[35],对本文采用的C2H4/Air两步化学反应模型计算常温常压、不同当量比下C-J爆轰波后的点火延迟时间,并与相同条件下Williams[36]详细化学反应机理获得的点火延迟进行比较,结果如图2所示。需要说明的是,该详细化学反应机理已经被广泛应用于各类碳氢氧燃料的爆轰计算,其可靠性已得到了大量验证[37-38]。另外,本文的点火延迟采用通用的定义,即点火开始到化学反应热释放速率最大所需要的时间,具体计算方法参见Damazo等[39]和Xiao等[40]的计算。从图2中可以看出,本文采用的C2H4/Air两步化学反应模型获得的点火延迟与Williams[36]详细机理的计算结果趋势完全一致,而且差别很小,尤其是在当量比为1附近,简化模型与详细机理吻合得非常好。因此,在综合考虑精度与计算资源的情况下,本文采用该两步化学反应模型开展C2H4/Air的三维旋转爆轰数值模拟。 图2 两步C2H4/Air化学反应模型验证Fig.2 Validation of two-step C2H4/Air chemical model 图3 t=1 000 μs时不同网格尺寸的温度分布云图Fig.3 Temperature distribution contour with different grid sizes for t=1 000 μs 1.3.2 一维爆轰管算例验证 为验证数值方法对爆轰波的捕捉能力,对一维爆轰管进行计算。计算域总长0.5 m,初始时刻填充压力0.1 MPa,温度300 K下当量比为1的C2H4/Air预混混合物。左侧边界为壁面,右侧为开放边界。通过在计算域左侧设置长0.005 m、压力3.0 MPa、温度3 500 K的点火区域来触发爆轰。表2所示为一维爆轰波传播速度与理论C-J速度的比较,其中C-J速度通过NASA CEA 计算得到[41]。计算使用3种不同大小的网格(0.5 mm、0.3 mm和0.1 mm),从中可以看出较好的网格收敛性,证明了求解器捕捉爆轰波的能力。 表2 计算值与理论C-J值的比较Tab.2 Comparison of calculated and theoretical C-J values 1.3.3 网格无关性验证 在同轴圆环RDC模型上分别对0.50 mm、0.30 mm、0.20 mm和0.15 mm的网格进行了计算,进气总压为0.6 MPa,总温为300 K。图3所示为0.001 s时刻不同网格尺寸计算得到的RDC温度场分布。由图3可以明显看出,尽管使用了不同的网格精度,但是从0.30 mm、0.20 mm和0.15 mm的计算结果来看,RDC内流场的基本特征,例如RDW、斜激波和滑移线都保持一致。图4给出了不同网格尺寸下的压力沿燃烧室入口的分布曲线。从图4中可以看出,使用0.30 mm、0.20 mm和0.15 mm网格得到的压力分布曲线显示出良好的一致性。表3列出了RDW传播稳定时流场参数的对比,可以看出网格尺寸对RDW波头高度、质量流量、RDW传播速度有一定影响。但当网格尺寸为0.3 mm时,继续降低网格尺寸对RDC流场的主要特征已经影响较小。这些对比都表明0.3 mm的网格精度已经收敛,满足当前三维RDC的计算精度要求。因此,本文计算中使用0.3 mm的计算网格。 图4 t=1 000 μs时刻燃烧室入口周向压力分布随网格尺寸的变化Fig.4 Change of pressure distribution along the inlet circumferential direction with the grid size for t=1 000 μs 表3 不同网格的计算结果对比 表4列出了数值模拟的参数设置。保持预混可燃混合物C2H4/Air的当量比为1,进气总压为0.6 MPa不变,分别对同轴圆环形和凹腔基环形两种不同结构的RDC进行数值模拟,进气总温依次设置为300 K、600 K和800 K。根据数值模拟结果,分析RDC的流场分布、RDW的传播特性以及燃料的燃烧属性。 表4 数值模拟参数Tab.4 Numerically simulated parameters RDC在0时刻通过高温高压区域点火成功,在新鲜可燃混合物的支持下,形成了稳定自持传播的RDW。图5分别给出了工况1和工况2流场稳定时的温度分布云图,显示出两种构型RDC内流场的主要特征。首先,如图5(a)所示,新鲜可燃混合物从RDC进口喷入,RDW沿圆周方向传播,爆轰产物周向膨胀并沿轴向从出口排出。在RDW波前形成较为规整的三角形新鲜燃料填充区。爆轰波和斜激波之间的温度间断为滑移线,此线为两次循环中爆轰产物的接触面,爆轰波、斜激波、滑移线的交汇结构保持了流场的稳定性[18]。对比图5(b)中凹腔基环形RDC的温度场分布,发现两种构型RDC流场存在不同。主要有凹腔基环形RDC中新鲜喷注混合物与燃烧产物的接触界面位置出现了明显的褶皱[42],另外RDW的波阵面也相对不规整。 图5 工况1和工况2的温度分布云图Fig.5 Temperature contours in Case 1 and Case 2 图6给出了工况2条件下RDW波头前周向角δ=0.1 rad截面带有流线的温度分布图。图6中,绿色虚线标出的为位于凹腔底部的局部高温区域,即Z1区域;R1和R2分别标记了流场中的两个漩涡,R1处的漩涡使得新鲜的混合物与燃烧产物进行掺混,提高了部分波前新鲜混合物的温度,即Z2区域;R2位于凹腔收缩段上游最低层(z=30~40 mm),该处的回流区导致了凹腔内流速降低、压力升高。将Z1和Z2位置的温度和压力分布放大如图7所示。由图7可以看出,Z1位置为一块高温高压的燃烧产物驻定区域,呈三角形,部分燃料在该位置以爆燃形式燃烧,印证了Peng等[27]在实验中发现凹腔回流区存在驻定的等压燃烧火焰。 图6 工况2条件下流线和温度分布Fig.6 Distribution of temperature and streamline in Case 2 图7 图5中Z1和Z2区域放大图Fig.7 Enlarged views of Z1 and Z2 in Fig.5 图8所示为工况2中不同轴向截面的温度分布以及局部的C2H4质量分数(YC2H4)分布。由图8可以看出:当z=1 mm位置时RDW波前存在部分新鲜混合物向凹腔内侧膨胀的现象,图中用白线圈出;随着轴向位置的增大,当z=5 mm 时,从温度云图上看爆轰波前混合物有小部分区域温度升高,图中用绿色虚线圈出并标记为P1;将爆轰波波前C2H4的质量分数放大显示于右下角,发现有少量的C2H4在爆轰波到达之前已经提前燃烧。燃料提前燃烧的现象随着z的增大愈加明显,具体表现为RDW波前高温区域(P2、P3)的面积增大、温度升高;当z=15 mm时,在RDW波前基本没有新鲜可燃混合物。因此轴向位置增高,RDW波前新鲜混合物的温度升高,并发生不同程度的提前燃烧现象。这种波前混合物温度升高和提前燃烧现象,在实验中可以促进活性较低的碳氢燃料实现爆轰[26];但是过度的提前燃烧也会降低RDC内爆轰消耗的燃料比例,从而降低RDC的性能[17-18]。 图8 工况2条件下不同轴向截面的温度分布和C2H4质量分数(YC2H4)分布局部放大图Fig.8 Distribution of temperatures at different axial cross sections and enlarged view of C2H4 mass fraction(YC2H4)in Case 2 图9(a)和图9(b)分别给出了工况1和工况2在不同轴向位置的面平均压力和面平均马赫数的变化,另外在图9(a)的顶部给出了凹腔的二维视图。从图9(a)中可以看出:在凹腔收缩段上游(z<40 mm),工况2 沿程的面平均压力大于工况1;在凹腔收缩段位置(蓝色虚线框出),工况2面平均压力下降迅速,在出口位置面平均压力小于工况1。图9(b)为面平均马赫数分布。由图9(b)可以看出:在凹腔收缩段上游,工况2 沿程的面平均马赫数分布小于工况1;在凹腔收缩段位置,工况2面平均马赫数迅速增加;最终工况2中出口位置面平均马赫数约为1.07,明显大于工况1中出口位置面平均马赫数0.87。通过对比工况2和工况1的面平均马赫数和面平均压力分布可知:工况2在凹腔的收缩段上游,流速较低,静压较高,大部分流动处于亚音速状态;在凹腔的收缩段,流道收缩导致流动加速,最终在RDC出口位置,工况2面平均马赫数大于工况1,面平均静压则低于工况1。凹腔的存在明显导致靠近凹腔上游流速降低,静压升高,这与Liu等[28]的实验分析结果一致。 图9 工况1和2沿z轴方向的面平均压力和马赫数分布Fig.9 Surface average pressure and Mach number along z-direction in Case 1 and Case 2 表5对比了不同工况的数值模拟结果。由表5可见:在同轴圆环形RDC中,当进气总温从300 K增加至800 K时,爆轰波的传播模态都表现为单波模态;在凹腔基环形RDC上逐步提高进气总温至800 K,爆轰波以同向三波模态传播,传播频率为33.38 kHz。这种现象可能是由进气总温升高和RDC构型改变两方面导致的。Wang等[43]和杨鹏飞等[44]分别通过数值模拟研究了进气总温对RDC流场的影响,都得出了爆轰波数目随进气总温增高而增多的结论。同时,凹腔提高了爆轰波波前反应物的温度,增加了RDC内的局部热点转变为爆轰波的可能性[45]。另外从表5中还可以看出,凹腔基环形RDC结构中RDW的速度亏损略高于同轴圆环结构。根据2.1节的分析,这可能是因为凹腔基环形RDC中爆轰波波前的新鲜可燃混合物不仅存在向出口方向的膨胀[46],还有向燃烧室凹腔内侧的膨胀,侧向膨胀效应的增强导致了RDW传播速度较低。 表5 数值模拟结果对比Tab.5 Comparison of numerically simulated results 图10给出了工况 5和工况 6在流场稳定时在中间层展开的温度分布图。由图10可以看出:在流场稳定后,工况5的流场内只存在一个自持传播的RDW,波头高度H=18.7 mm;与工况5相对应的工况 6,其采用凹腔基环形构型,RDW的传播模态发生了明显改变,即为同向三波模态;3个RDW的波头高度基本一致,约为5 mm,证明流场基本稳定,RDW稳定自持传播。图11所示为工况 6三波模态在监测点(22.5 mm,0 mm,0.001 mm)处的压力演变过程。从图11中可以看出:在起爆之后,经过一段约0.2 ms的转变过程后,燃烧室内自发地形成了3个能够自持传播的RDW;计算总共持续了1.4 ms,3个同向传播的RDW在燃烧室内循环了十几个周期并逐渐趋于稳定,在爆轰波稳定传播阶段,其压力峰值(约4.6 MPa)基本一致,表明流场处于稳定状态。 图10 工况5和工况6中间层展开的温度分布Fig.10 Distribution of Temperature at the middle layer in Case 5 and Case 6 图11 工况6监测点处的压力演变Fig.11 Evolution of pressure at the monitoring point in Case 6 图12给出了稳定时刻靠近燃烧室入口位置的压力沿中心半径分布。由图12可见:工况5为同轴圆环RDC构型, 外壁面为压缩曲面,内壁面为发散曲面,内外壁面流体存在流动偏折和流程参数不匹配,导致RDW侧向弯曲,波后存在明显的激波反射现象[42],反射激波在内壁面和外壁面之间来回反射并逐渐衰减;由于凹腔基环形RDC燃烧室入口位置内壁面对爆轰波的约束性较弱,从工况6的燃烧室入口位置压力曲线中没有发现明显的激波反射现象。 图12 工况5和工况6中燃烧室入口位置(z=1 mm)沿中心半径的压力分布Fig.12 Distribution of pressure near inlet (z=1 mm) along middle radius in Case 5 and Case 6 对于理想的同轴圆环形RDC模型,燃料主要以爆轰的形式被消耗,爆燃主要位于新鲜燃料与已燃气体的接触界面[14,16]。但是根据以上分析及已有的研究[26-28],对于凹腔构型RDC,部分燃料同时会被驻留于凹腔的高温已燃气体提前引燃。这无疑增加了爆燃消耗的燃料比例,本节通过引入热释放速率分数(fHRR)量化不同热释放速率(HRR)消耗的燃料占比。 (19) 图13 1.2 ms时刻工况1中使用着色的温度与热释放速率的散点图Fig.13 Scatter plot of temperature and heat release rate colored by Case 1 at 1.2 ms 图14所示为工况1和工况2在不同临界HRR下的fHRR分布。由图14可以看出:对于工况1,93%的C2H4以大于1012J/(m3/s)的热释放速率被消耗,75.1%的燃料以大于1013J/(m3/s )的热释放速率被消耗;对于工况2,85.4%的C2H4以大于1012J/(m3/s) 的热释放速率被消耗,64.1%的燃料以大于1013J/(m3/s )的热释放速率被燃烧;随着临界HRR增大,工况2与工况1之间的fHRR差别越明显,即工况2以高热释放速率消耗的C2H4相对工况1更低,表明工况2相对于工况1以爆轰形式消耗的C2H4比例降低。 图14 不同临界HRR条件下工况1和工况2的fHRR分布Fig.14 Heat release rate fraction(fHRR)distributions of Case 1 and Case 2 under different critical HRRs 图14所示给出了不同工况在临界HRR=1012J/(m3/s)条件下fHRR(fHRR>1012 J/(m3/s))和推力F的分布。其中推力F通过(20)式计算得到: (20) 式中:下标outlet表示在燃烧室出口截面位置进行面积分。从图15中不同构型RDC的热释放速率分数随进气总温的变化曲线可以看出:同轴圆环RDC中fHRR>1012J/(m3/s)大于凹腔基环形RDC,当进气总温为800 K时,同轴圆环RDC中fHRR>1012J/(m3/s)最小,即67.9%。表明在该工况中67.9%的燃料以大于1012J/(m3/s)的热释放速率被消耗;当进气总温为800 K时,凹腔基环形RDC中fHRR>1012 J/(m3/s)最小,即54.3%,表明该工况中54.3%的燃料以大于1012J/(m3/s)的热释放速率被消耗。因此,凹腔会导致燃烧室内爆轰消耗的燃料比例降低。当在同一RDC构型下,fHRR>1012J/(m3/s)随温度的增大而降低,表明燃料温度的升高也会导致RDC内爆燃消耗的燃料增多[18]。 图15所示为不同工况中fHRR>1012J/(m3/s)和推力的分布。由图15可知:在相同进气总温条件下,同轴圆环RDC的推力大于凹腔基环形RDC;同一RDC构型中,推力随温度增加呈现出降低趋势。Wang等[43]也发现了相同规律,即fHRR>1012 J/(m3/s)和推力随燃烧室构型和进气总温的变化表现出相同的趋势,表明RDC内爆轰消耗的燃料占比增多时,其推力也增大。 图15 不同工况中fHRR>1012J/(m3/s)和推力的分布Fig.15 Distribution of fHRR>1012J/(m3/s) and average thrust in different cases 本文在开源计算流体力学软件OpenFOAM框架内,通过求解N-S方程开展了C2H4/Air三维连续旋转爆轰流场的数值模拟,对比了同轴圆环和凹腔基环形两种构型RDC中爆轰波的传播特性,深入分析了不同进气总温下的RDC流场特征和燃料燃烧特性。得到主要结论如下: 1)对于凹腔基环形RDC,在凹腔内部存在明显的回流区,凹腔内流速较低、静压较高,在凹腔收缩段流动加速。相对相同进气条件的同轴圆环RDC,其出口面平均马赫数增大,面平均压力降低。凹腔的存在导致新鲜可燃混合物与燃烧产物掺混,在提高波前反应物温度的同时也加剧了RDC内的爆燃现象。在凹腔基环形RDC中,受新鲜可燃混合物向出口和凹腔内壁方向的侧向膨胀影响,爆轰波速度亏损在相同条件下大于同轴圆环形RDC。 2)在相同进气条件下,同轴圆环RDC相对于凹腔基环形RDC以爆轰形式消耗燃料占比更多。另外,当RDC构型一致时,随进气总温升高,爆轰消耗燃料占比也降低。RDC中的燃料以爆轰形式消耗的比例提高时其推力也增大。 3)保持进气总压0.6 MPa,当总温分别为300 K和600 K时,同轴圆环RDC和凹腔基环形RDC中RDW的传播模态保持一致,均为单波模态。增大进气总温至800 K,凹腔基环形RDC自发地形成同向三波模态,而同轴圆环RDC仍为单波模态。另外,相对于同轴圆环RDC,凹腔基环形RDC头部位置爆轰波后激波反射现象明显减弱。1.3 计算方法验证及网格无关性分析


2 计算结果与讨论
2.1 凹腔对RDC流场的影响



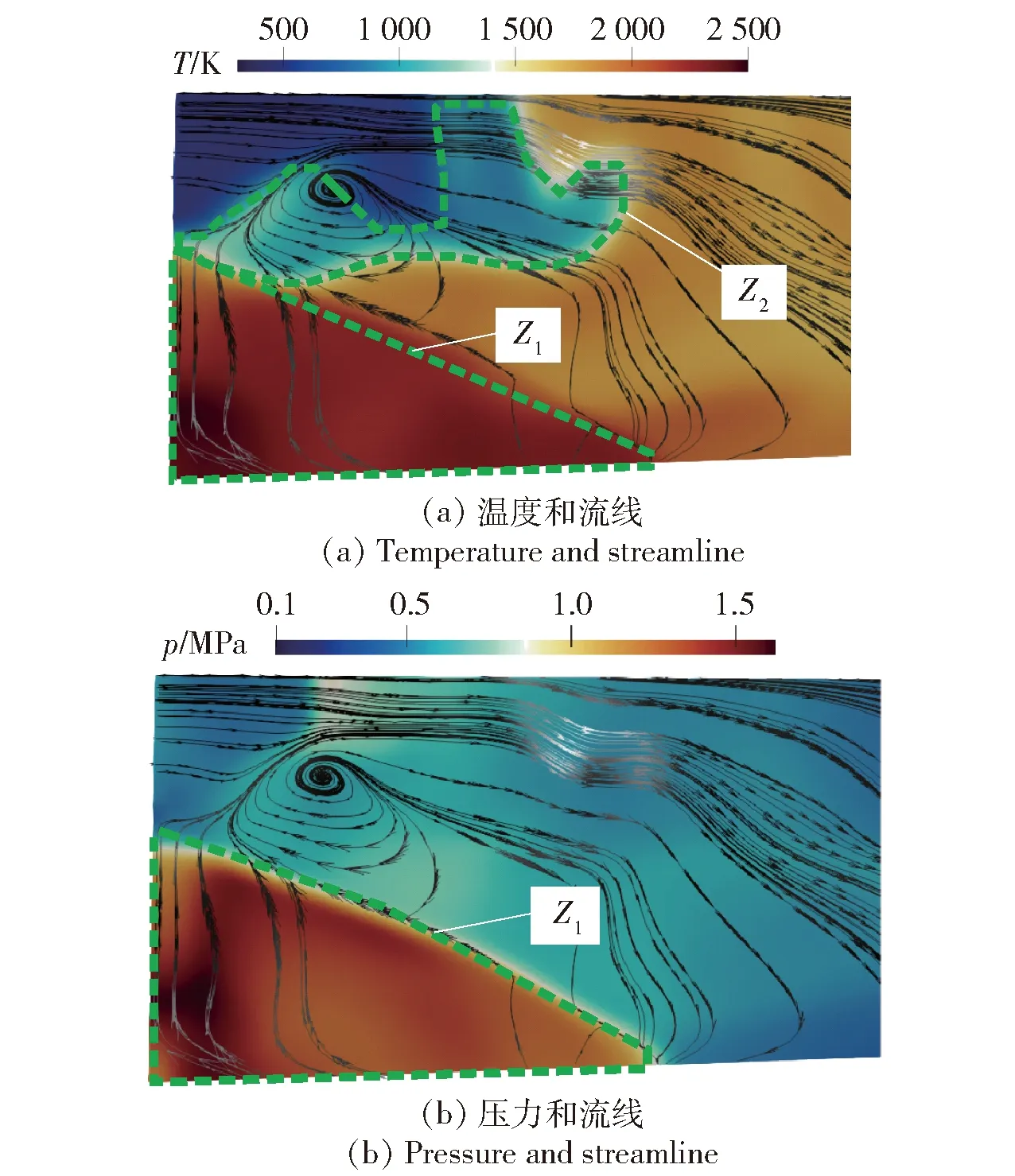


2.2 凹腔对RDW传播的影响
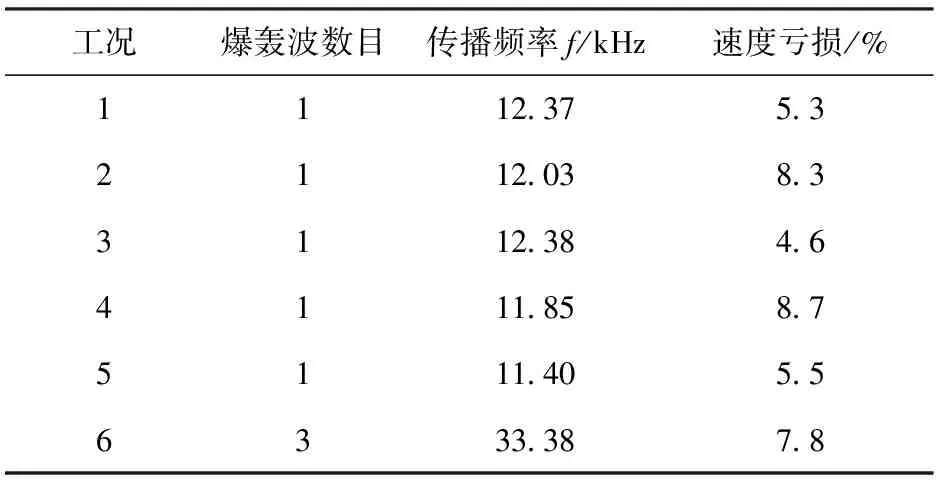


2.3 凹腔对C2H4燃烧属性影响

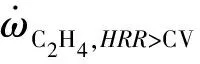

3 结论

