基于人工神经网络的非球形破片阻力系数预测模型

辛大钧， 薛琨

(北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081)

0 引言

战斗部爆炸后，由于爆轰驱动的作用会形成大量高速飞行破片，初速度马赫数在5以上，这些破片的速度在空气中受空气阻力的作用而逐渐衰减，落地之前将会有70%以上的时间处于亚声速飞行状态。因此，了解和掌握破片在超声速至亚声速区间内的速度衰减规律才能预测破片的弹道轨迹和不同距离处的残余动能，对于评价破片式战斗部毁伤效果以及评估安全距离均有重要意义。

破片在空气中飞行时主要受重力及空气阻力的作用，空气阻力主要与破片的飞行速度、迎风面积、空气密度以及空气阻力系数有关。其中阻力系数作为影响空气阻力的关键因素具有重要研究意义。之前的研究表明，阻力系数主要与破片形状以及飞行速度有关，国内外学者对此开展过一系列研究。

一般认为破片速度与阻力系数呈现先增后减趋势，峰值点出现在马赫数1.4左右，国内外学者使用弹道枪试验对不同形状的典型破片(球形、立方形、圆柱形等)进行了一系列研究，大量的弹道枪研究结果表明，对于不同形状的破片，阻力系数与马赫数的关系仅仅是趋势类似，不同马赫数下阻力系数的数值最高点出现的位置均明显不同，因此研究者一般认为阻力系数还受破片形状的影响。

关于形状对阻力系数的影响，Dunn等在对回收的炮弹破片进行阻力系数测试后，发现非规则破片的阻力系数显著大于球形、立方形等规则破片，首次提及了破片形状对阻力系数的影响。破片形状一般用破片和球体的近似程度来表征。Dehn使用破片的最大迎风面积除以破片的平均迎风面积，即=/，或者破片体积的2/3次方除以破片平均迎风面积/作为描述破片形状的参数，对于规则形状破片，等于柯西迎风面积即1/4表面积，对于不规则破片，可通过正二十面体测量仪测出32个方向上的迎风面积取平均。McCleskey使用垂直风洞测试了大量翻滚非规则破片在马赫数0.1下的阻力系数，首次比较系统地建立起了马赫数0.1下阻力系数与Dehn定义的形状参数之间的关系，并认为所有破片的阻力系数随马赫数的变化规律与球形破片一致，通过这种假设可以将不规则破片马赫数0.1下的阻力系数试验结果外推至跨音速及超音速区间。Miller进一步使用风洞及弹道枪对McClescky报告中的破片进行了阻力系数测试，得到跨声速及超声速段的阻力系数结果，与McClescky的外推结果相比明显偏大。因此，简单地对球形破片阻力系数规律进行外推，无法精确地获得非规则破片跨声速及超声速速度下的阻力系数。Moxnes等重新分析了McClescky的试验结果，认为破片阻力系数与的相关性比更好，应该用作为描述破片形状的参数。

由于非球形破片在空气中会发生不规则翻滚，当前研究随机翻滚状态下破片的平均阻力系数比较理想的方法是采用弹道枪试验，但弹道枪试验成本较高，且无法覆盖所有的破片形状，对破片尺寸也有要求，很难开展大规模试验。因此众多研究者借助数值模拟的方法来研究这一问题，Moxnes等用6自由度计算流体动力学(CFD)方法模拟了无约束破片在静止流场中的自由飞行，并对阻力系数在时间上进行了微秒量级的平均。但由于计算资源有限，这种方法很难对破片飞行全过程进行模拟，且需要人为给破片施加初始的翻滚力矩，与实际破片经历爆轰驱动后的初始运动状态有一定区别。

为了研究大量非球形破片的形貌在超声速至亚声速范围内对破片阻力系数的影响，本文选择采用流动流场中固定破片的数值计算方法。该方法的关键是如何对破片不同迎风方向下的阻力系数进行平均，等效破片随机翻滚状态下的阻力系数。提出一种基于正二十面体的阻力系数平均方法，计算了大量不同形状破片在不同马赫数下的阻力系数，并采用与含义一致但学术上更通用的球形度代替，=π6/(π/)。发现阻力系数受形状参数和马赫数的影响规律很难使用单一函数准确描述。因此本文采用近年来发展迅速的深度神经网络模型对阻力系数的影响因素进行拟合，获得了相对准确实用的阻力系数预测模型。

1 数值模拟方法及验证

1.1 球形破片阻力系数模拟方法

以直径7 mm球形破片空气阻力系数的数值模拟为例，介绍数值计算模型。

数值模拟采用破片固定，流场采用给定速度运动的方式。将进行模拟的球形破片划分方形外流场区域，球形破片(直径为)的球心与入流边界距离为40，与出流边界的距离为40，与各个侧边界的距离为20。网格划分为四面体非结构化网格，流场中网格的最小尺寸定为1.00 mm，破片壁面附近的网格尺寸为0.10 mm。体网格总数约60 000个，数值模拟建模如图1所示。

图1 数值模拟Fig.1 Numerical modeling

求解器选择Fluent 17.0，当马赫数大于0.3时，设置为可压缩流动。湍流模型选择S-A湍流模型，主要用以求解一个有关涡黏性的运输方程，计算量相对较小。对逆压梯度的边界层问题和壁面限制的流动问题有较好的计算结果，通常应用于空气动力学问题中。设置流场域四周为压力远场边界条件，用于模拟无穷远处的自由流条件；流场材料设置为空气，状态为理想气体，并用萨兰德定律修正空气黏度。球形破片表面设置为无滑移壁面，用于限定流体和破片区域。

差分格式选择为压力- 速度耦合方法；压力插值采用标准格式；空间离散用Roe-FDS(Flux-Difference Splitting)格式，该离散方式具有很高的间断分辨率和黏性分辨率；扩散项离散采用中心差分格式；对流项离散采用2阶迎风格式。

根据上文的数值计算模型，对直径7 mm的球形破片在马赫数为0.1～6.0速度区间的阻力系数进行模拟。流场静压云图如图2所示。

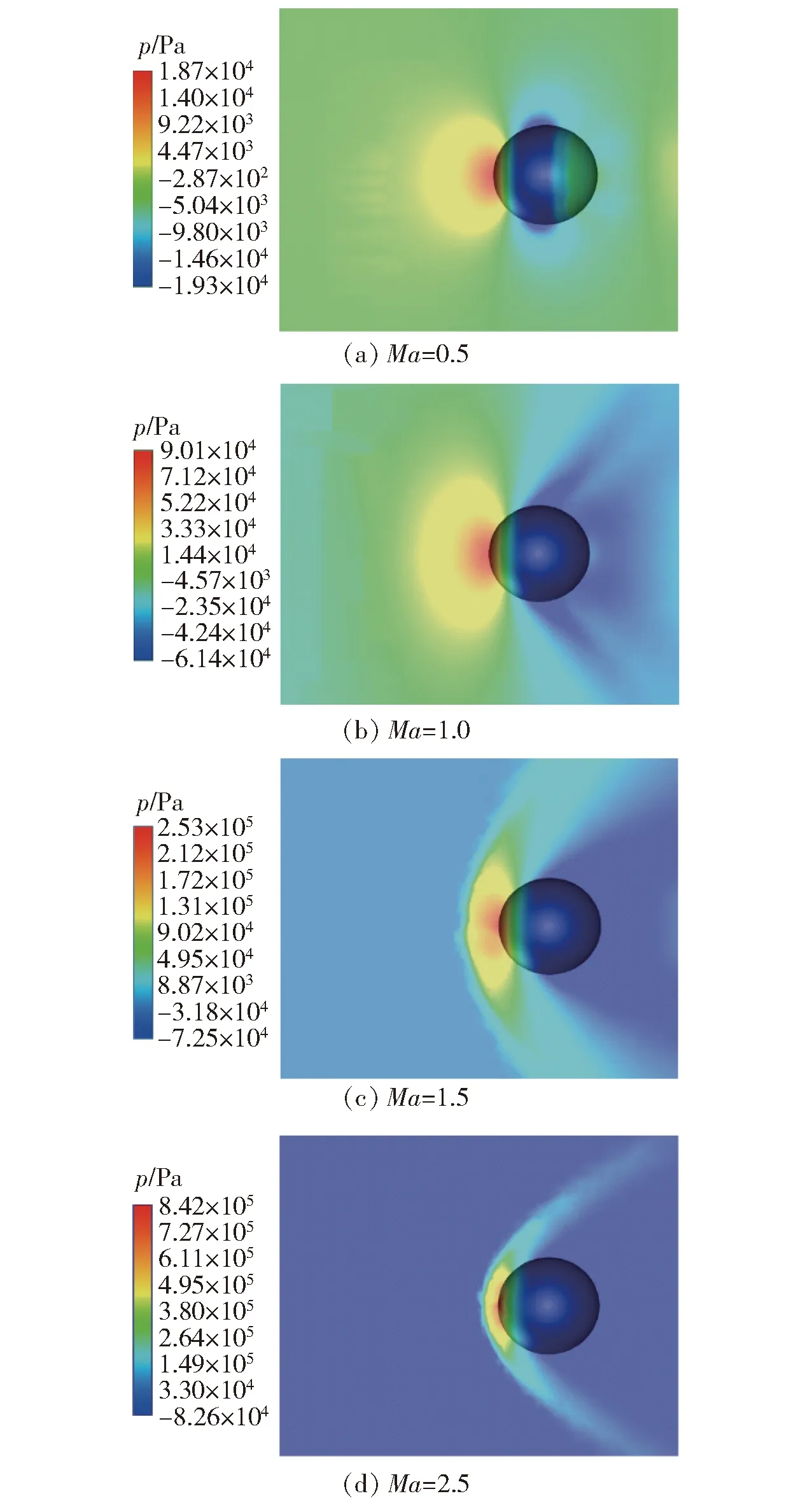
图2 直径7 mm球形破片压力云图Fig.2 Pressure field around φ7 mm spherical fragment

由图2可知：破片处于亚声速流场时，在来流前端会形成一个高压区，来流末端会形成一个低压区，此时压差阻力和摩擦阻力是空气阻力的主要来源；随着飞行马赫数的提高，来流前端的压力逐渐升高，高压区会逐渐收窄并向破片两侧弯曲，形成一道弓形激波，此时波阻是阻力的主要来源。

本文对文献[4]球形破片弹道枪试验结果进行了复现，破片的飞行速度范围是马赫数为1.5～6.0，将试验结果以及文献[4]中给出的弹道枪试验结果与本文数值模拟结果进行对比，如图3所示。

图3 球形破片数值模拟结果与文献[4]试验以及本文复现试验结果对比Fig.3 Comparison of numerical results of spherical fragments with experimental data in Ref. [4] and those repoduced in this paper

由图3可见，模拟结果在破片飞行马赫数小于0.5时，相比弹道枪试验结果略微偏小，在破片处于跨声速以及超声速飞行状态时，模拟结果与试验结果匹配得较好。总体而言，破片飞行马赫数小于0.5时阻力系数基本保持不变；飞行速度达到跨声速时阻力系数迅速升高，在马赫数为1.4附近达到最大值，此后飞行速度继续增加，阻力系数略有下降。

球形破片数值模拟结果与试验结果数值对比如表1所示。由表1可见：马赫数为0.7时，数值模拟结果与试验结果相对误差最大，为-11.62%；马赫数为3.0时，数值模拟结果与试验结果相对误差最小，为0.37%，误差范围未超过15%。

1.2 非球形破片阻力系数计算方法

非球形破片不同姿态下的迎风面积和阻力系数与破片姿态密切相关，如图4所示。将非球形破片固定在笛卡尔坐标系中，迎风方向的单位矢量为(，)，其中表示与其在平面内投影向量的夹角，表示在平面内投影向量与轴的夹角。

破片处于随机翻滚状态时，不同迎风方向对应着不同的阻力系数(，)，而各个迎风方向在空间上出现的概率相同。因此理想状态下，需要对所有迎风状态下的阻力系数进行平均：

表1 球形破片模拟结果与试验对比Tab.1 Comparison of numerical results of sphericalfragments with experimental data

图4 非球形破片迎风方向示意图Fig.4 Upwind direction of non-spherical fragment

(1)

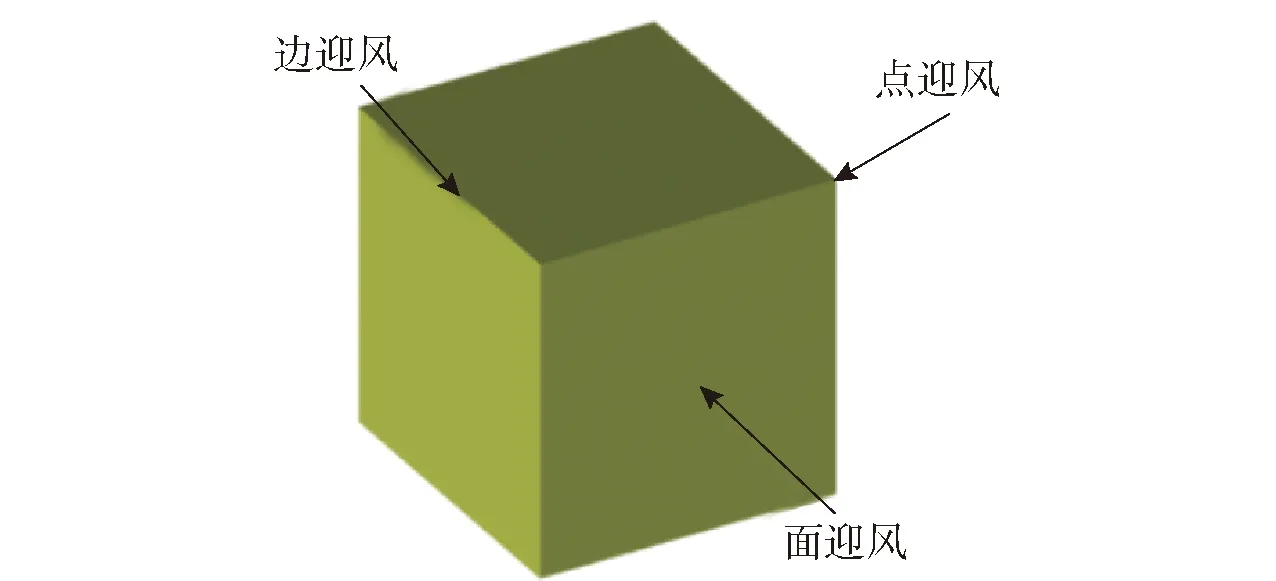
图5 立方体三类迎风状态示意图Fig.5 Three types of upwind state of the cube

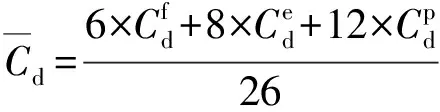
(2)

上述平均方法可以在一定程度上估计方形破片的阻力系数，但对于任意形状破片而言，该方法并不具有普适性。理论上，从正多面体中心指向各个面心或顶点的方向可以较好地实现对空间的平均划分，而正多面体一共有5种，其中面最多，最接近球体的正多面体为正二十面体。基于此，美国军用装备国际试验操作规程(ITOP)4-2-813测量平均迎风面积的方法中采用正二十面体测量仪的方法得到不规则破片的平均迎风面积。具体做法如下：将破片放在虚拟正二十面体的中心，从正二十面体的中心指向其20个面心(，=1，2，…，20)与12个顶点(，=1，2，…，12)，产生32个方向。沿这32个方向对破片进行投影，可以得到对应的投影面积，即20个中心- 面心方向的投影面积和12个中心- 顶点方向的投影面积。这些投影面积求平均后得到的平均投影面积，可以等效破片的平均迎风面积。图6所示为正二十面体平均方法示意图。

图6 正二十面体平均方法示意图Fig.6 Schematic diagram of the icosahedron averaging method

破片在弹道飞行时的迎风面积和阻力系数均与破片姿态存在一一对应的强依赖关系，因此破片自由翻滚状态下平均迎风面积的等效方法也适用于平均阻力系数。借鉴美国军用装备国际试验操作规程(ITOP)4-2-813测量平均迎风面积的方法，同样采用正二十面体法对非球形破片的平均阻力系数进行等效计算。具体做法如下，首先采用11节中给出的数值方法计算得到流场方向沿20个中心- 面心连线和12个中心- 顶点连线的破片阻力系数，d和d，然后将这些阻力系数平均，以等效破片随机翻滚状态下的平均阻力系数，

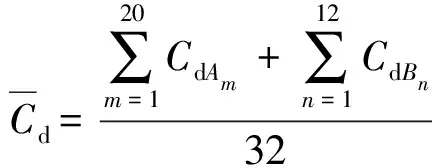
(3)

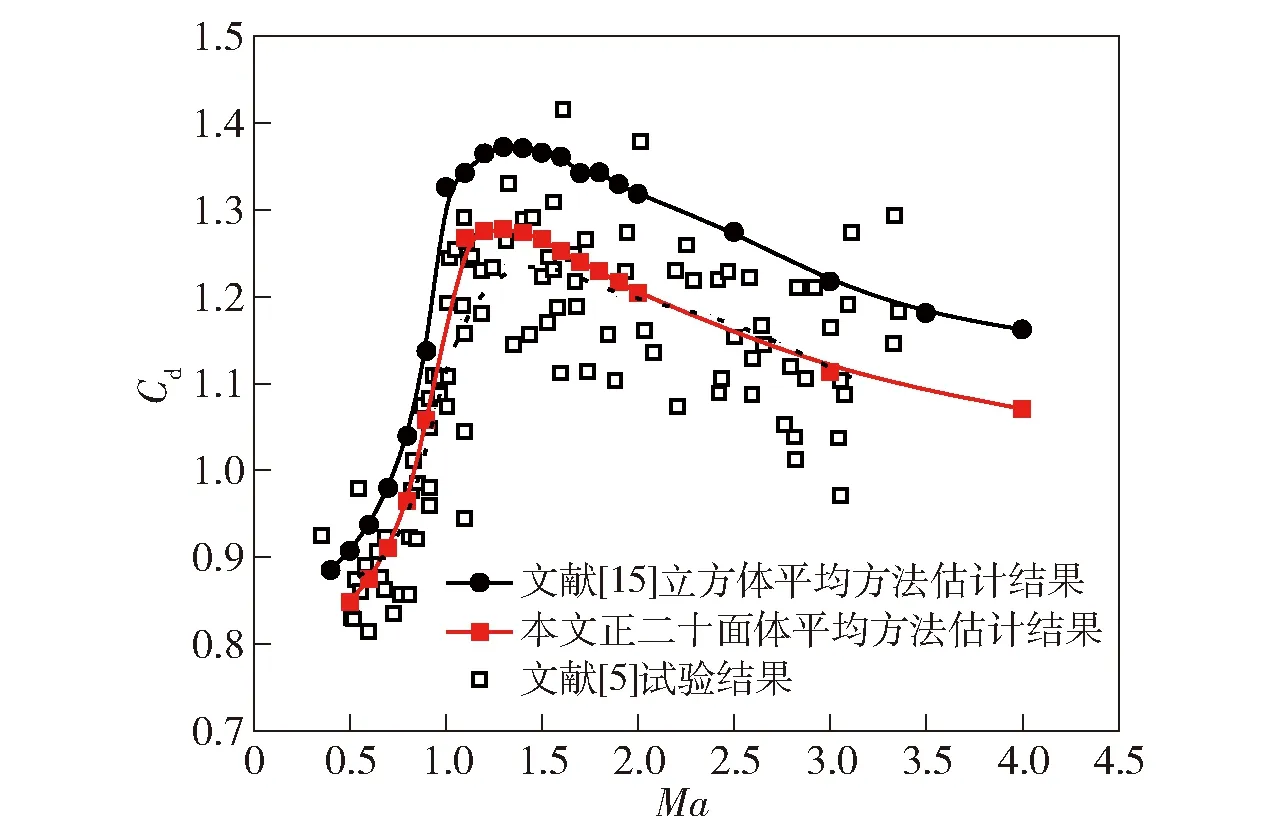
图7 立方体破片模拟结果与试验结果对比Fig.7 Comparison of numerical results of cubic fragments with experimental data

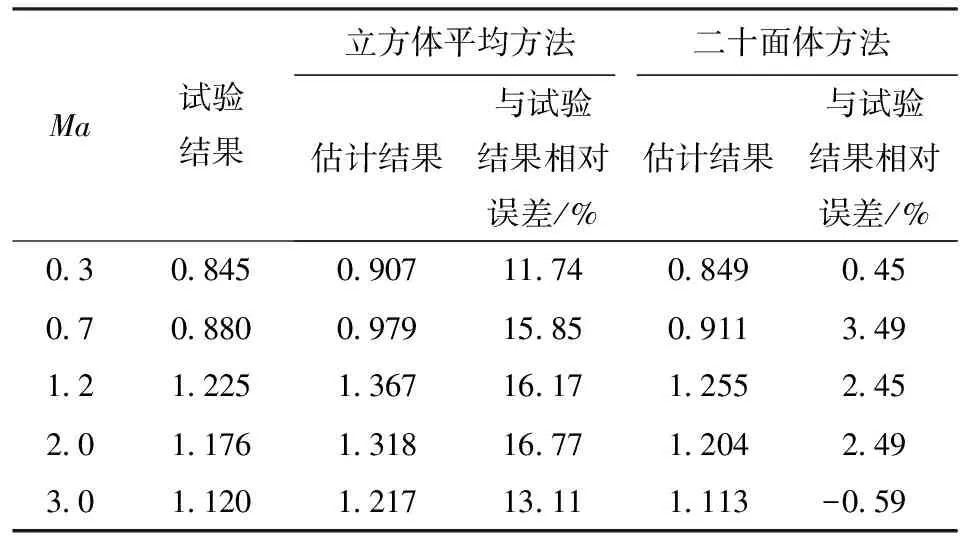
表2 不同平均方法平均阻力系数对比Tab.2 Comparison of different averaging methods

图8比较了正二十面体法计算得到的圆柱形破片(长径比为1)在不同马赫数下的平均阻力系数和文献[6-7]的试验结果。由图8可见，等效平均阻力系数曲线可以较好地穿过弹道枪试验的散点，再次验证了正二十面体平均方法对非球形破片在随机翻滚状态下平均阻力系数的等效有效性。

图8 圆柱体破片模拟结果与试验结果对比Fig.8 Comparison of numerical results of cylindrical fragments with experimental data

2 破片形状对阻力系数影响规律

为考察破片形状对随机翻滚状态下破片平均阻力系数的影响，采用正二十面体法计算得到不同形状破片的平均阻力系数。为了扩大结论的适用范围，破片形状包括了球形、长方体、圆柱体、三棱柱等规则形状，也包括一部分静爆试验回收的不规则破片，图9展示了其外观、建模和网格化的过程。为进一步丰富样本的类型，还通过球谐函数生成了一系列形状不规则的破片外形并引入样本中，通过球形度描述破片的形状，所有的破片样本统计结果如表3所示。图10所示为马赫数01下不同球形度破片的平均阻力系数。显然，在破片马赫数为01时，平均阻力系数与球形度存在显著的负相关。图10中同时给出了McClescky垂直风洞试验的结果。值得注意的是，McClescky垂直风洞试验采用的是非规则破片，非规则破片在马赫数01时平均阻力系数与球形度的相关性与各类形状破片相同，表明球形度是影响破片平均阻力系数重要的形状参量，可以作为一种统一的参数对破片形状进行描述。

图11给出了不同球形度破片在跨声速和超声速飞行时的平均阻力系数。由图11可见：在跨声速和超声速飞行时，破片平均阻力系数与球形度的负相关性仍然存在，但相关性明显减弱；特别是球形度低于06的破片，平均阻力系数与球形度的相关性变得非常不显著。

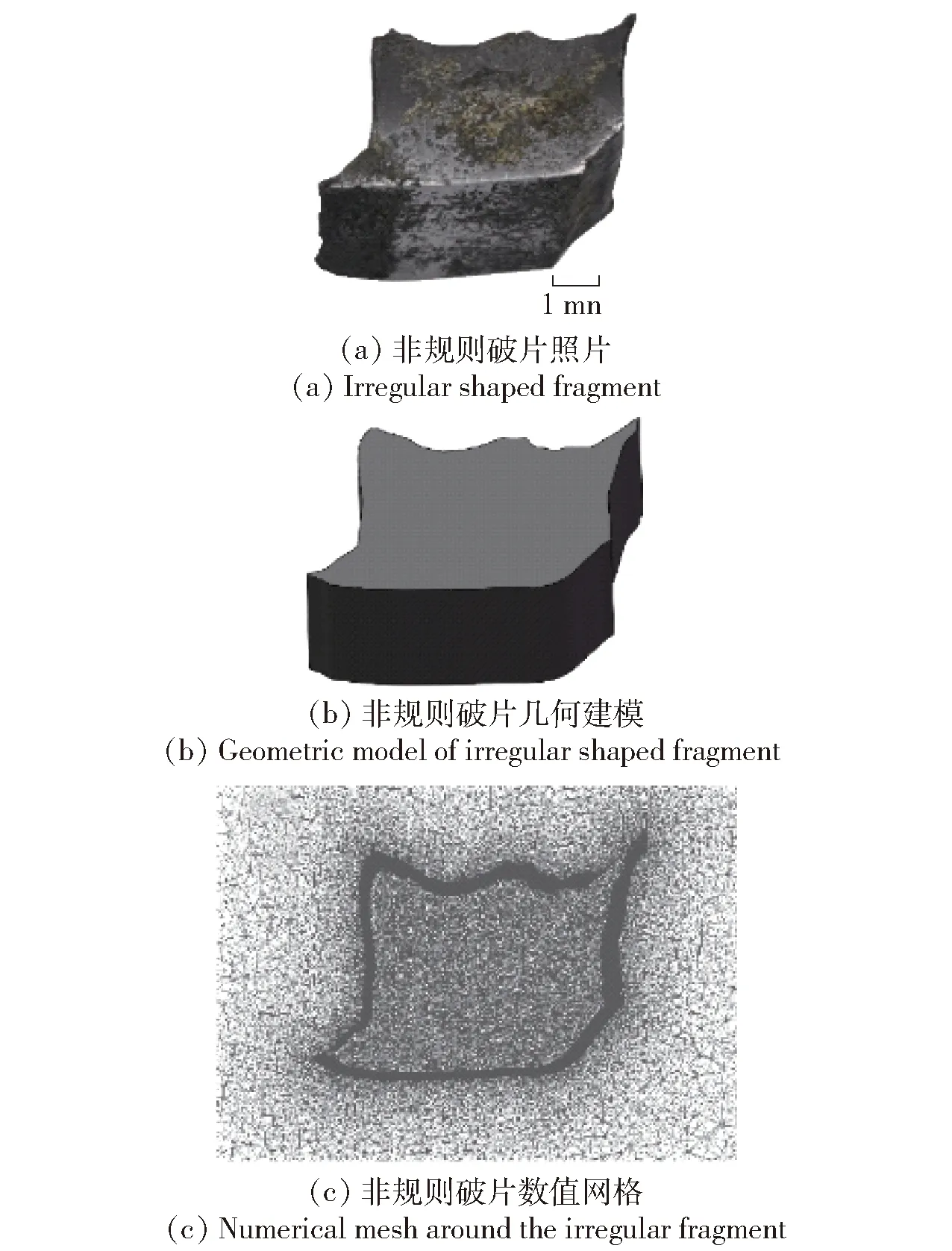
图9 爆炸回收非规则破片建模过程Fig.9 Modeling process of irregular fragment recovered from the detonation

表3 数值模拟破片外形统计

图10 不同形状破片模拟结果与垂直风洞试验结果比较Fig.10 Comparison of numerical results of different shapes of fragments with vertical wind tunnel experimental data

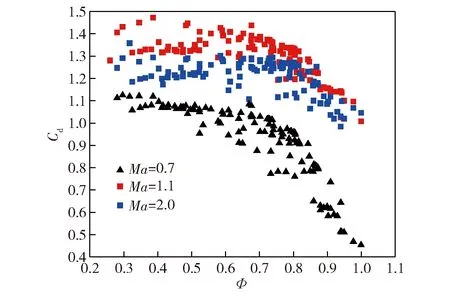
图11 不同马赫数下阻力系数与球形度的关系Fig.11 Drag coefficient versus sphericity under different Mach numbers

从图10、图11中可以看出，阻力系数与球形度明显相关，但二者很难通过简单的函数关系进行拟合，且不同飞行速度下球形度和阻力系数的关系也明显不同。基于此，本文采取人工神经网络模型建立阻力系数综合预测模型。

3 阻力系数预测模型的建立

3.1 人工神经网络模型

由引言可知，影响破片阻力系数的参数主要包括破片形状和飞行马赫数，因此本文采用人工神经网络拟合的方式构建(，)。

人工神经网络是指在输入参数和输出参数之间有若干层隐藏的神经网络，人工神经网络具有很强的复杂非线性系统建模能力，能够刻画难以用解析式表达的高维映射。一个典型人工神经网络结构如图12所示，包含一个输入层、一个输出层以及两层隐藏层，每一个节点都是一个神经元(见图13)，每个神经元接受来自前一层的神经元不同权重的值，经神经元内激活函数处理后向下一层传播。图12中，、、、分别为神经网络输入参数，、、分别为不同层之间神经元连接的权重向量，、、分别为不同层之间神经元连接的偏移量，(=1，2，3)、分别为第1层、第2层神经元的输入值，、分别为第1层、第2层神经元的输出值，为神经网络模型的输出值。图13中，、、、分别表示该神经元接受上一层不同神经元输出的权重值，表示偏移量，为该神经元的输入值，为该神经元输出值，()表示激活函数。

图12 人工神经网络结构Fig.12 Structure of artificial neural network

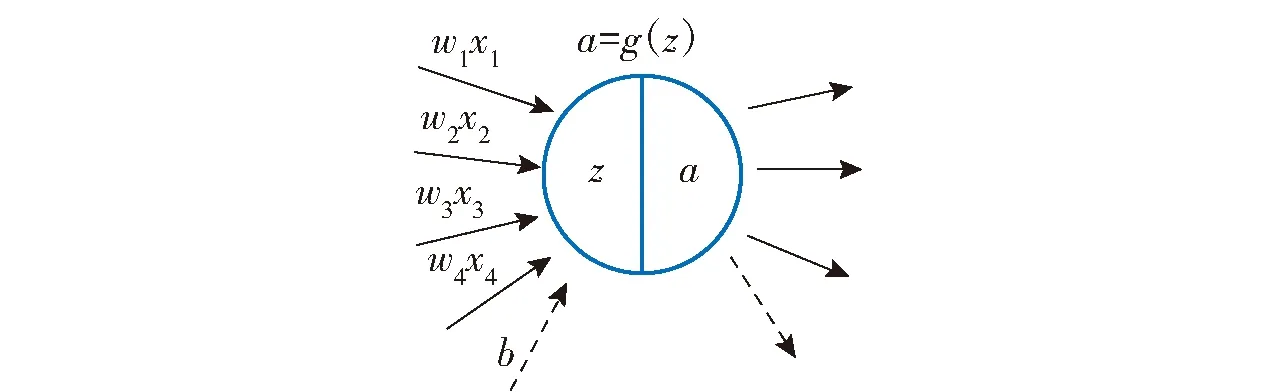
图13 神经元Fig.13 Neuron

神经元的输入为前一层神经元的输出的线性组合：

(4)

输入神经元的值经过激活函数()处理后继续向后传播：

=()

(5)

本文使用Softplus函数作为神经元的激活函数，是因为当输入值>0时Softplus函数梯度较大，迭代过程可以较快达到收敛，Softplus函数表达式如(6)式，函数图像如图14所示。

()=ln(1+e)

(6)

图14 Softplus激活函数Fig.14 Softplus activation function

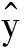
(7)

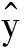
损失函数是神经网络参数、的函数，因此神经网络需要迭代找到使损失函数最小的、，采用的迭代方法是梯度下降算法，损失函数对神经网络参数的梯度通过链式求导法则获得，即神经网络的向后传播算法。本文采用Adam优化算法对神经网络进行优化，在向后传播基础上，以一定学习率不断更新模型的权重，使其梯度不断下降，损失函数的值不断减小。

3.2 阻力系数预测模型

本文搭建的人工神经网络模型，输入参数为影响破片阻力系数的因素，包括球形度以及马赫数，输出参数为阻力系数。对数值模拟计算得到的712个数据样本进行拟合，同时为了防止过拟合，随机选择其中的600个样本点进行模型训练，其余样本点用于模型验证。训练样本的空间分布如图15所示。搭建包含3个隐藏层，每个隐藏层包含20个神经元的神经网络模型。图16所示为模型训练过程中训练集以及验证集的损失函数的变化曲线，可以看出迭代到100 000步之后，训练集和验证集的损失函数实现了收敛，损失函数值均降低到0003以下。表明该神经网络模型没有出现过拟合或欠拟合状态，拟合效果比较理想。训练完成后得到的阻力系数预测模型如图17所示，训练得到的不同球形度下阻力系数与马赫数的关系如图18所示。

图15 训练样本的空间分布Fig.15 Spatial distribution of training samples

图16 损失函数变化曲线Fig.16 Changing curves of loss function

图17 神经网络阻力系数模型训练结果Fig.17 Neural network-based drag coefficient prediction model

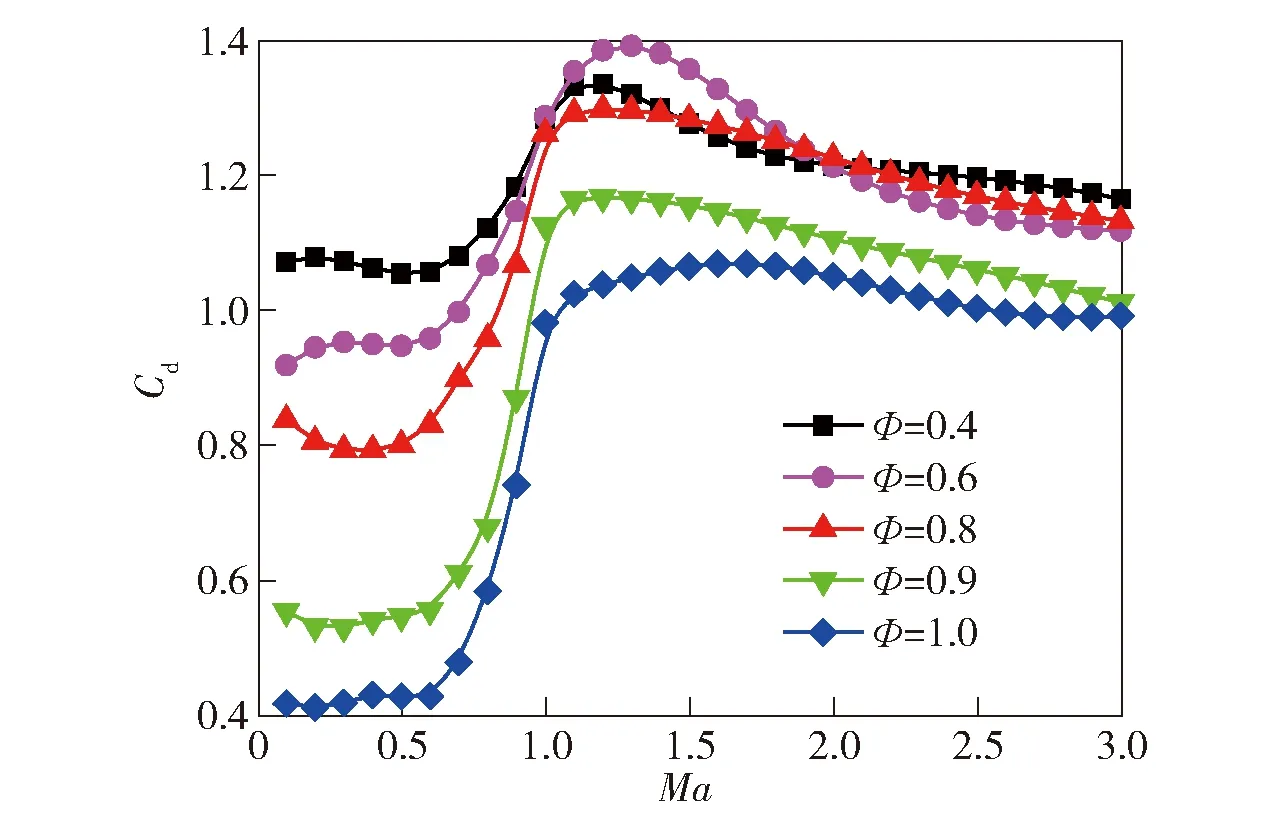
图18 训练得到的不同球形度下阻力系数与马赫数的关系Fig.18 Drag coefficient versus Mach number for different sphericities trained by ANN

图17中阻力系数预测模型可以较好地对(，)进行拟合。任意形状的破片在任意飞行速度下的阻力系数预测值可以从图17所示的结果中得到。图18为训练得到的不同球形度下阻力系数与马赫数的关系。从图18中可以看出，不同球形度破片的阻力系数随马赫数变化的曲线形状类似但数值明显不同：当破片飞行速度较小时，破片形状会显著影响阻力系数；当飞行马赫数大于2时，形状对阻力系数的影响变得不明显。

3.3 模型泛化能力评价

神经网络的泛化能力是指神经网络在训练完成以后神经网络对测试样本或工作样本做出正确反应的能力。在完成模型训练后，本文进一步计算了3种破片(球形度分别为046、076和091)在超声速至亚声速区间内的阻力系数作为该预测模型的测试样本。不同的破片阻力系数模拟值与模型的预测值的对比如图19(a)、图19(b)、图19(c)所示，图19(d)为所有测试点的预测值与模拟值的相对误差。

从图19中可以看出，神经网络阻力系数预测模型可以很好地预测3种破片的阻力系数曲线，测试结果相对误差均小于3，表明该模型具有较强的泛化能力。

神经网络训练得到的阻力系数预测模型可用于破片的外弹道轨迹计算中，实现根据破片的实际形状赋予其相应的阻力系数曲线。为进一步验证阻力系数预测模型的适用性，特别是针对非规则破片的适用性，将预测模型应用于文献[11]中非规则破片的轨迹计算，并与弹道枪实测阻力系数计算出的轨迹进行对比(见图20)。该破片为爆炸测试场回收的不规则破片，经测试，球形度为058，质量为314 g，初始速度1 524 m/s，飞散角度为20°。从图20中可以看出，使用神经网络预测模型得到的轨迹计算结果与弹道枪实测结果的吻合程度相当好，最终神经网络模型计算得到的落点位置为429 m，弹道枪实测阻力系数结果得到的落点位置为432 m，相对误差07，计算精度完全可以满足破片弹道计算的要求。

图19 不同球形度破片模型预测阻力系数与数值模拟结果对比Fig.19 Comparison between the predicted drag coefficient and the numerically simulated results of fragments with different sphericities

图20 使用不同阻力模型数值计算的破片运行轨迹对比Fig.20 Trajectories of fragments calculated with different drag models

4 结束语

本文采用正二十面体平均方法对非球形破片高速飞行状态的空气阻力系数进行数值模拟，得到形状以及马赫数对破片阻力系数的影响规律，通过人工神经网络建立了预测破片阻力系数的模型。得出主要结论如下：

1) 各类形状破片的空气阻力系数随马赫数的增加均呈现先增大后逐渐减小的规律，但数值明显不同，形状对阻力系数存在明显影响。

2) 对于非球形破片，正二十面体平均方法是一种估计破片随机翻滚状态下的阻力系数的有效方法，可应用于任意形状破片的阻力系数计算中。

3) 本文建立的人工神经网络阻力系数预测模型可以较好地描述马赫数以及破片形状对阻力系数的影响，且具有良好的泛化能力，可以利用其进行其他非球形破片阻力系数的预测。