切削深度对PDC齿超高速破岩机理的影响分析*
李其州 张 凯 周 琴 凌 雪 刘宝林 王 悦
(中国地质大学(北京)工程技术学院;自然资源部深部地质钻探技术重点实验室)
0 引 言
近年来,PDC钻头以其广泛的地层适应性、良好的稳定性以及设计的高灵活性等特点,被广泛应用于油气资源的勘探开发过程并逐渐占据了油气开采行业70%以上的市场[1]。随着地下资源勘探逐渐向深硬地层推进,低钻速和高能耗成为影响PDC钻头钻进效率的主要因素。除此之外,机械钻速同样受到钻进参数和PDC钻头结构的直接影响[2]。超高转速金刚石钻进技术具有破岩能耗低、钻进效率高等优点,可以在显著提高机械钻速的同时大幅降低钻压和能量输入,从根本上降低钻井成本,提高经济效益,是大深度、高硬度和高研磨性地层钻进的有效提速手段。
国内外钻探工作者近年来逐渐开始对超高转速金刚石钻进技术进行探索。美国能源部于2002年开展了超高转速金刚石钻进技术的相关研究。TerraTek实验室研究发现,通过应用高转速(大于10 000 r/min)金刚石钻进技术,可以实现更高效的岩石破碎。A.D.BLACK等[3]对不同转速条件下金刚石钻头的破岩性能进行了试验研究,测试结果表明转速越高,成本效益越大。Smith Neyrfor公司与美国TerraTek实验室合作,综合考虑破岩效率与破岩能耗,对超高转速金刚石钻进的可行性进行了研究,研究结果表明,超高转速条件下,转速越高,硬岩破碎效率越高,能耗越低。GAO M.Y.等[4]通过建立PDC切削齿高速切削有限元分析模型发现,当切削速度超过8 m/s时,切削齿热通量和破碎比功都随着切削速度的增大而减小。
目前,国内外的相关研究大多关注的是超高转速金刚石钻进技术的可行性及其钻进性能,并未对超高转速条件下具体的破岩规律进行深入探讨。而在常规转速领域已开展了众多研究。E.DETOURNAY等[5]在前人研究结果的基础上,提出了切削齿与岩石的相互作用模型,将作用在切削齿上的力分解为前刀面上的切削力以及磨损面上的摩擦力。T.RICHARD等[6]通过单齿试验研究发现,根据切削深度的不同,岩石破碎共有两种失效形式。V.RAJABOV等[7]通过大量试验发现,刀具后倾角、侧倾角、切削深度以及岩石类型等因素对破碎比功都有显著影响,并建立了一个考虑刀具后倾角和侧倾角的PDC切削齿-岩石三维力学模型,其模拟结果与试验数据相符合。张在兴等[8]采用有限元仿真模拟方法分析了切削深度对切削齿温度变化的影响规律。
国内外试验和有限元仿真分析研究表明,转速以及切削参数等对刀具破岩性能的影响较为显著,其中切削深度更是改变岩石破坏模式的重要因素。但在超高速条件下,切削深度对PDC切削齿破岩响应规律的研究尚有欠缺。因此,有必要对超高转速条件下切削深度对PDC钻头破岩机理进行深入研究,这对于解析超高转速条件下钻头与岩石间的相互作用、突破转速瓶颈至关重要。超高转速条件下,试验方法难以捕捉整个破岩过程的细节,而有限元分析方法可以有效地模拟PDC切削齿破岩的全过程。因此,本文利用有限元模型分析方法,针对超高速条件下切削深度对PDC切削齿的破岩机理的影响展开研究。
1 超高速切削模型数值模拟
1.1 材料模型
为了更真实地模拟PDC切削齿破碎岩石的过程,高明洋等[1]在研究中采用了以Drucker-Prager塑性模型为基础的切削材料模型,除此之外,还利用ABAQUS软件对UMAT子程序进行开发与调用。Drucker-Prager塑性模型可以表征与压力相关的各个量,被广泛应用于岩石切削领域。为保证分析的准确性,高明洋等选取B.AKBARI等[9]与伍开松等[10]的研究结果进行验证。验证结果表明,应力误差在15%左右,而热量的变化趋势与公开发表的研究结果相同,基本验证了所建模拟模型的可行性。因此本文继续采用其建立的材料模型。
1.2 几何模型定义及材料参数
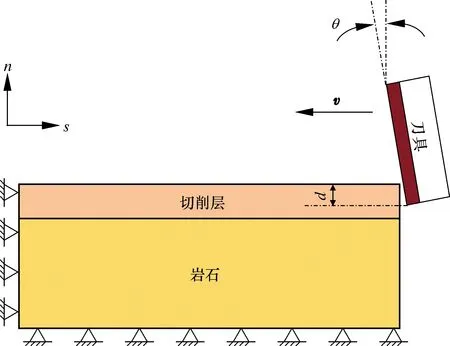
图1 PDC切削齿破岩模型示意图Fig.1 Rock cutting model of PDC cutter
图1为PDC切削齿破岩模型示意图。图1中s和n分别代表水平方向和竖直方向,v代表切削速度,θ为刀具后倾角,d为切削深度。其中切削齿直径为15 mm,厚度为6 mm;岩石长300 mm,高30 mm;刀具与岩石之间的摩擦因数为0.1,切削时长0.02 s。为保证计算精度,同时提高计算效率,对切削层以及刀具前刀面网格进行加密。该模型中PDC齿的导热率为543 W/(m·℃),密度为3 510 kg/m3,弹性模量为890 GPa,泊松比为0.07,比热容为190 J/(kg·℃);岩石材料的导热率为3.5 W/(m·℃),密度为2 650 kg/m3,弹性模量为40 GPa,泊松比为0.25,比热容为800 J/(kg·℃)。
1.3 模型边界条件及切削参数
将PDC钻头破岩过程简化为二维PDC切削齿线性切削岩石的二维模型,限制切削齿在竖直方向的位移,并在岩石底面和左边界施加固定约束,如图1所示。根据钻进过程的实际工况以及高明洋等[1]对切削速度区间的划分,当切削速度超过8 m/s时,即进入高速切削阶段。因此,给定切削齿和岩石初始温度为20 ℃,超高速以13 m/s为例,刀具后倾角为-10°,切削深度取0.3~1.9 mm,其改变间隔为0.1 mm。
1.4 切削模型验证
为验证切削模型的准确性,以切削速度2 m/s为例进行PDC切削齿破岩过程仿真模拟,得到的切削力F与切削深度d的关系如图2a所示。当切削速度较小时,切削力与切削深度存在两种不同的变化趋势:当d
1.5 评价指标
本文将通过表征切削效率的破碎比功(EMS)对数值模拟结果进行分析。EMS越低,破碎单位体积岩石所需的能量越小,其切削效率越高。研究超高速条件下EMS与切削深度的关系是优化设计超高转速钻进工艺的基本依据之一。全PDC钻头的EMS与钻压P、机械钻速v′、钻头面积Ab、转速n以及扭矩T密切相关。式(1)是由Teale推导得出的大气压条件下回转切削过程中EMS的计算方法:
(1)

图2 常规转速下切削力随切削深度的变化规律Fig.2 Change rules of cutting force with cutting depth at conventional speed
E.DETOURNAY等建立的关于锋利PDC切削齿的受力模型如图3所示。由于在二维线性切削模型中,切削齿在垂直方向上没有相对运动,系统中唯一做功的力是水平方向上的切削力,且并未考虑切削齿的磨损。因此,EMS的计算可以简化为[12]:
(2)
式中:Fcs为水平切削力,Ac为切削横截面积。
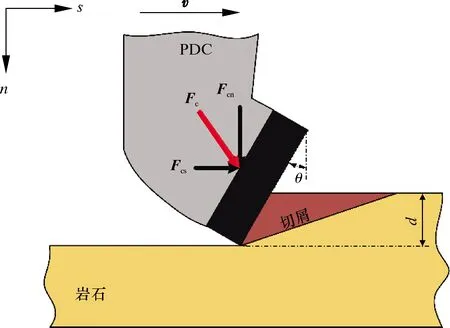
图3 锋利PDC切削齿受力模型示意图Fig.3 Forces acting on a sharp PDC cutter
2 岩石切削仿真结果分析
2.1 超高速条件下切削深度对EMS的影响
选取切削过程中相对稳定阶段的平均切削力计算EMS,仿真分析得出了超高速(v=13 m/s)条件下PDC切削齿EMS随切削深度的变化规律,如图4所示。EMS随着切削深度增大迅速下降,随后缓慢上升,其变化趋势与祝效华等[13]和V.RAJABOV等[7]的研究结果一致。由图4可知,d=1.4 mm时,EMS最小,PDC切削齿切削效率最高。由式(2)可知,EMS主要受水平切削力Fcs和切削横截面积Ac的影响。当后倾角为-10°,切削深度从0.3 mm增加到0.8 mm时,切削力增加了0.62倍,而切削面积增加了1.67倍,因此EMS急剧下降;当切削深度从0.8 mm增加到1.4 mm时,切削力增加了0.32倍,而切削面积增加了0.75倍,EMS持续降低,但下降速率有所减小;当切削深度从1.4 mm增加到1.9 mm时,切削力增加了0.51倍,而切削面积增加了0.36倍,因此EMS呈缓慢上升趋势。由此可以推断出,在超高速条件下,对于PDC切削齿切削深度存在最优值,使得切削效率最高,即对于不同PDC钻头都存在最优钻压,从而有效延长PDC钻头的使用寿命并提高钻进效率。
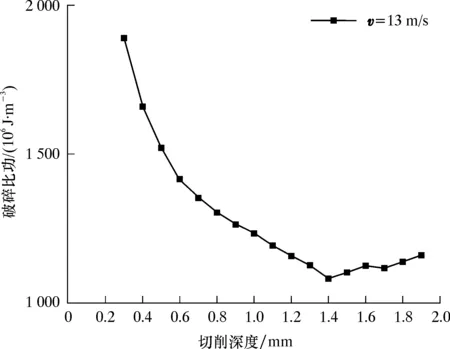
图4 超高速条件下EMS随切削深度的变化规律Fig.4 Change rules of EMS with cutting depth at ultra-high speed
2.2 超高速条件下切削深度对Fcs的影响
在二维线性切削模型中,Fcs、Ac是影响EMS的主要因素。为进一步探究在超高速切削过程中切削深度对EMS的影响,对超高速(v=13 m/s)切削过程中不同切削深度下的切削力进行了分析。Fcs随切削深度的变化规律如图5所示。图5表明其切削过程存在3个阶段。阶段Ⅰ,当d

图5 超高速条件下切削力随切削深度的变化规律Fig.5 Change rules of cutting force with cutting depth at ultra-high speed
3 讨 论
3.1 超高速条件下切削深度对切屑形成机理的影响
结合常规切削速度条件下的研究分析,超高速切削过程中切削深度对PDC切削齿切削效率与切削力等的影响可能与岩石的破坏模式有关。HUANG H.等[14]已经证实,切削深度是导致岩石破坏模式转变的重要因素,并且可以通过切屑的大小形状等特征来判断岩石的破坏模式。因此,探究不同切削深度下超高速切削的切屑形成机理对于丰富超高转速金刚石钻进技术基础理论有着十分重要的意义。
图6显示了超高速切削过程中,3个不同阶段形成的切屑。当d=0.5 mm时,切削过程中仅存在粉末状切屑,如图6a所示,表明岩石仅以塑性破坏失效。当d=1.3 mm时,切削过程中以大体积块状切屑为主,同时存在少量粉末状切屑,如图6b所示,表明岩石以脆性破坏失效为主并伴随着微弱的塑性破坏。当d=1.8 mm时,切屑组成与前一阶段相反,以小切屑为主,如图6c所示,表明岩石脆性破坏减弱,塑性破坏增强。

图6 不同切削深度下超高速切削形成的切屑形态Fig.6 Cutting chips with different cutting depths at ultra-high speed
通过对切屑大小和形状的分析,当处于不同阶段时,岩石的主要失效形式不同。当岩石被压碎时,Fcs轻微波动,逐渐增大;当岩石断裂分离时,Fcs剧烈波动,骤然下降[15]。为进一步探究d>dcr2(阶段Ⅲ)时脆性破坏减弱而塑性破坏加剧的原因,对不同切削深度下的切削力Fcs进行分析。
图7为d=0.5 mm(阶段Ⅰ)、d=1.3 mm(阶段Ⅱ)、d=1.8 mm(阶段Ⅲ)时切削力Fcs的变化规律。对比d=1.3 mm和d=1.8 mm时Fcs的变化规律可以发现,前者Fcs呈现锯齿状变化,表明切削过程中两个脆性切削周期间隔短,块状切屑连续而密集;而对于后者,其Fcs增至最大值后保持相对稳定,基本保持在较高水平,刀具压碎作用增强,表明切削过程中两个脆性切削周期间隔长,块状切屑独立而稀疏。当前刀面与岩石完全接触时,岩石更倾向于塑性破坏。由此可以推断,在超高速条件下,当d>dcr2(阶段Ⅲ),岩石内部的裂纹起裂扩展准则和裂纹相互作用方式发生了一定的转变,导致岩石难以产生裂纹,脆性切削作用减弱。
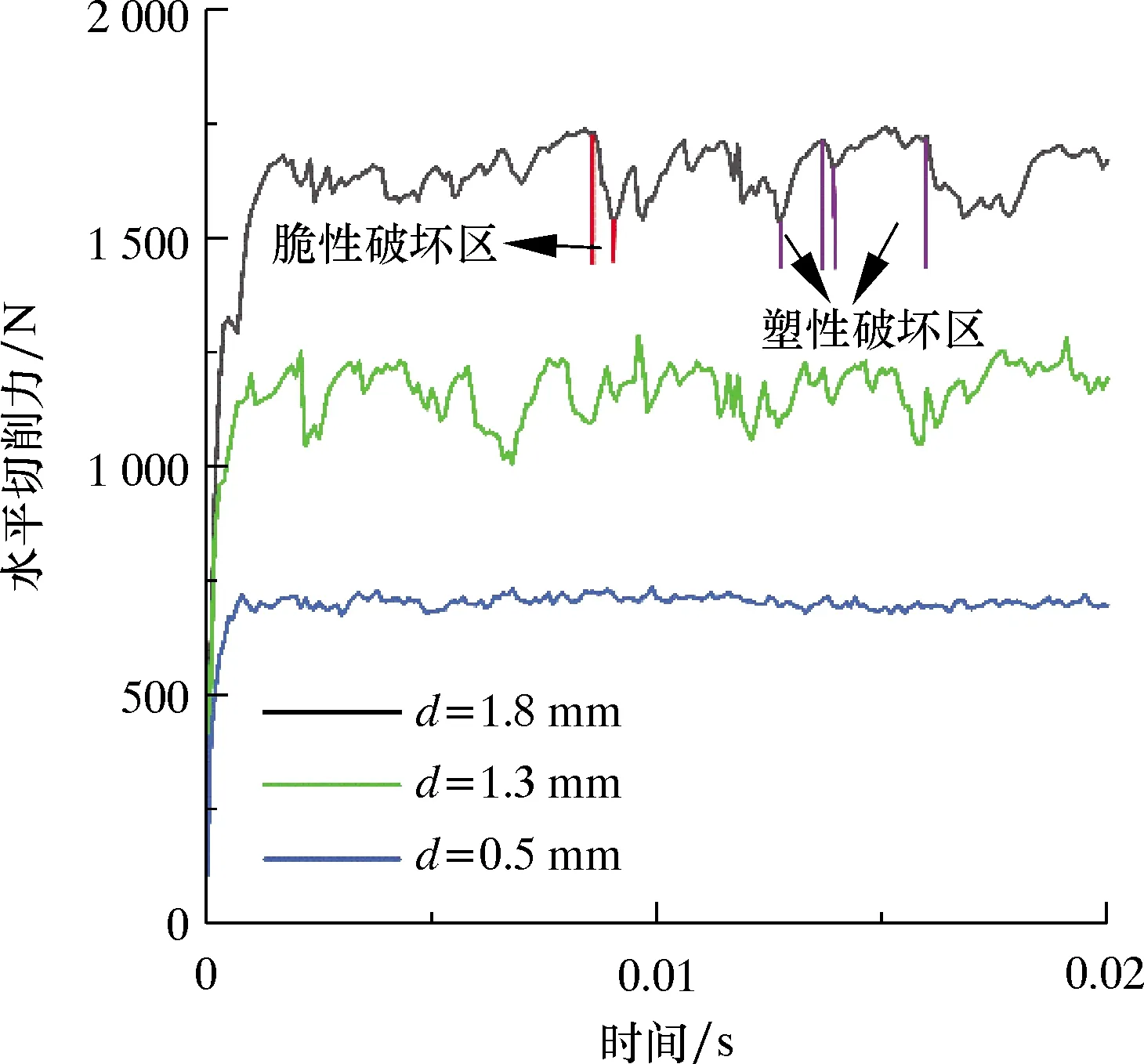
图7 塑性破坏和脆性破坏的切削力Fig.7 Cutting forces in plastic failure mode and brittle failure mode
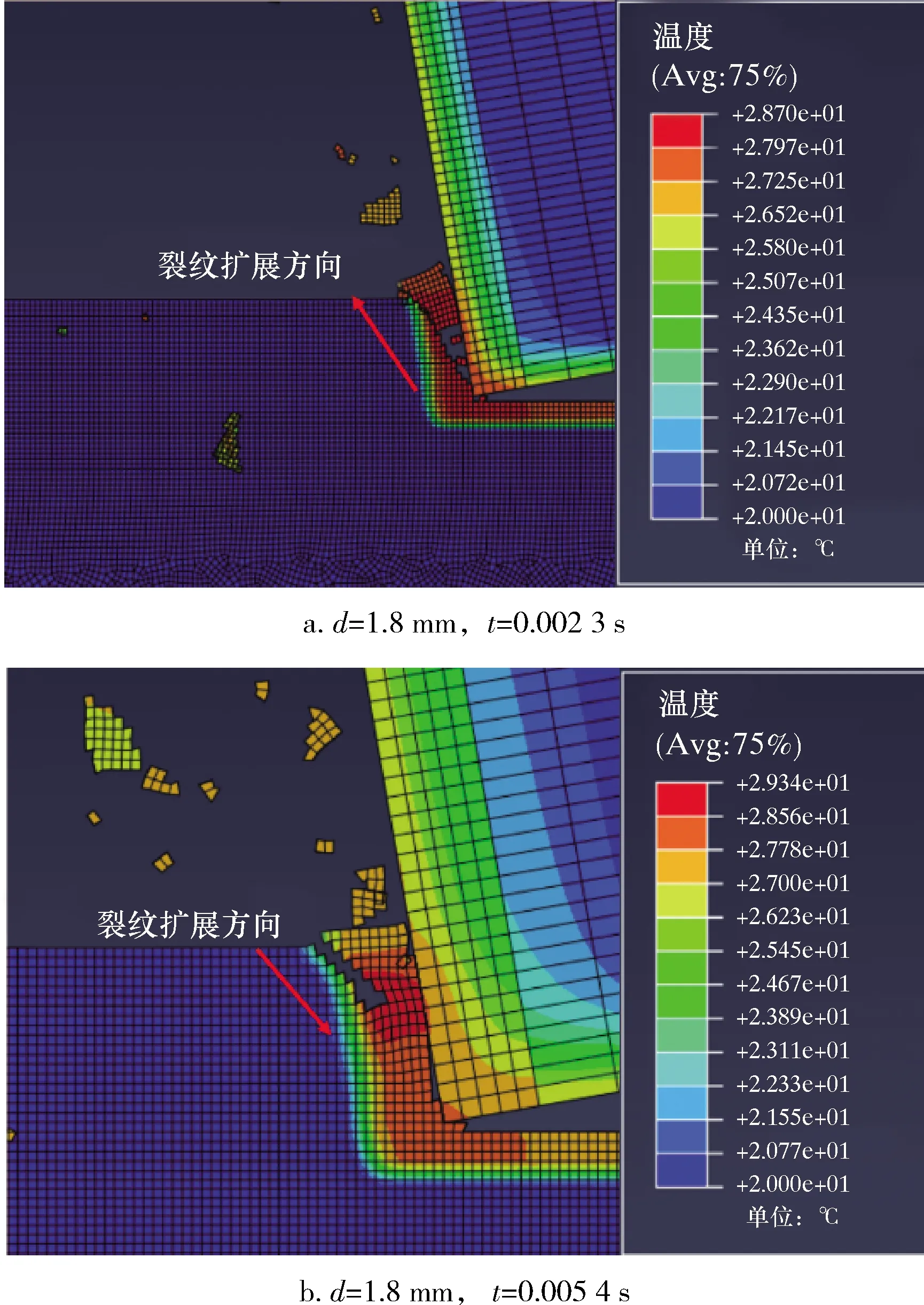
图8 d=1.8 mm时不同时刻两种不同的裂纹扩展方式Fig.8 Two different crack propagation modes at different time with d=1.8 mm
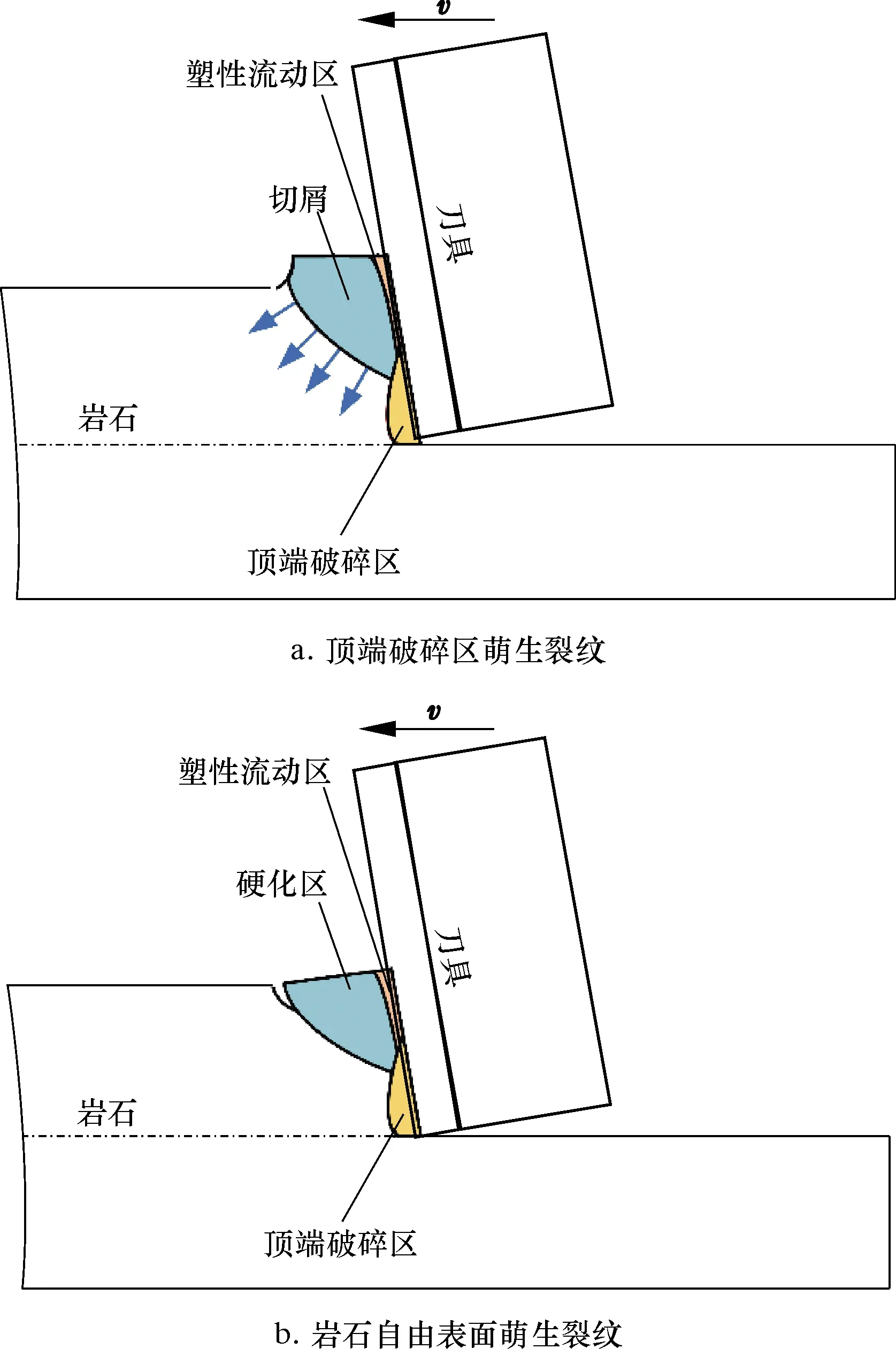
由上述分析可知,岩石的破碎方式与裂纹的萌生扩展密不可分。观察d=1.8 mm(阶段Ⅲ)时的切削过程发现,不同时刻岩石裂纹的初始萌生位置存在明显差异,如图8所示。当切削齿与岩石接触,刀尖处会形成一个顶端破碎区[16-17]。裂纹容易在顶端破碎区域的边界上产生,随后扩展至岩石自由表面,如图8a所示。除此之外,裂纹还可能会在岩石自由表面处萌生,如图8b所示。M.C.SHAW等[18]基于试验在金属切削领域也观察到了相同的现象,并提出了周期性断裂理论。基于该理论,在超高速切削过程中,在刀具前方岩石自由表面处产生了硬化区,在挤压作用下向自由表面隆起。由于脆性材料抵抗断裂的能力要低于抵抗滑移的能力,所以,更容易在自由表面萌生裂纹。在超高速切削过程中,这两种裂纹萌生机理同时存在。
不同的裂纹扩展方式会影响切屑的大小和形状,当不同形状的切屑被去除后,前刀面与岩石接触情况将会改变,如图9所示。当岩石在靠近刀尖处断裂时,前刀面岩石呈现斜坡状,如图9a所示;当岩石在前刀面中部断裂时,前刀面岩石将呈现断崖状,如图9b所示。通过观察d=1.8 mm的切屑形成过程,当d>dcr2(阶段Ⅲ)时岩石断裂方式以后者为主。由图9可知,随着切屑的逸散,刀尖处始终与岩石接触,而前刀面上部则与岩石间歇性不连续接触。这两种不同的岩石断裂方式会导致前刀面的受力并非均布。图10为d=1.8 mm(阶段Ⅲ)时前刀面各节点的受力和其标准差示意图。由图10可知,越靠近刀尖处,切削齿受力越稳定,前刀面受力维持在较高水平。因此,当d>dcr2(阶段Ⅲ)时,超高速切削过程中的有效切削深度呈动态变化。当前一个切屑被去除后,有效切削深度减小,岩石塑性破坏加剧。
综上所述,在超高速切削过程中,当d>dcr2(阶段Ⅲ)时,由于裂纹萌生与扩展机制的改变,岩石不仅难以产生裂纹,脆性切削作用减弱,而且随着有效切削深度的减小以及较高的冲击载荷,刀具压碎作用加剧,岩石塑性破坏再次占据主导地位,使得切削效率降低,EMS增大。这与超高速切削过程中冲击载荷加剧以及岩石特性有关[19]。另外,ZHOU Y.N.等[20]也已从能量的角度证明切削齿后倾角对岩石破坏模式的转变存在一定的影响。
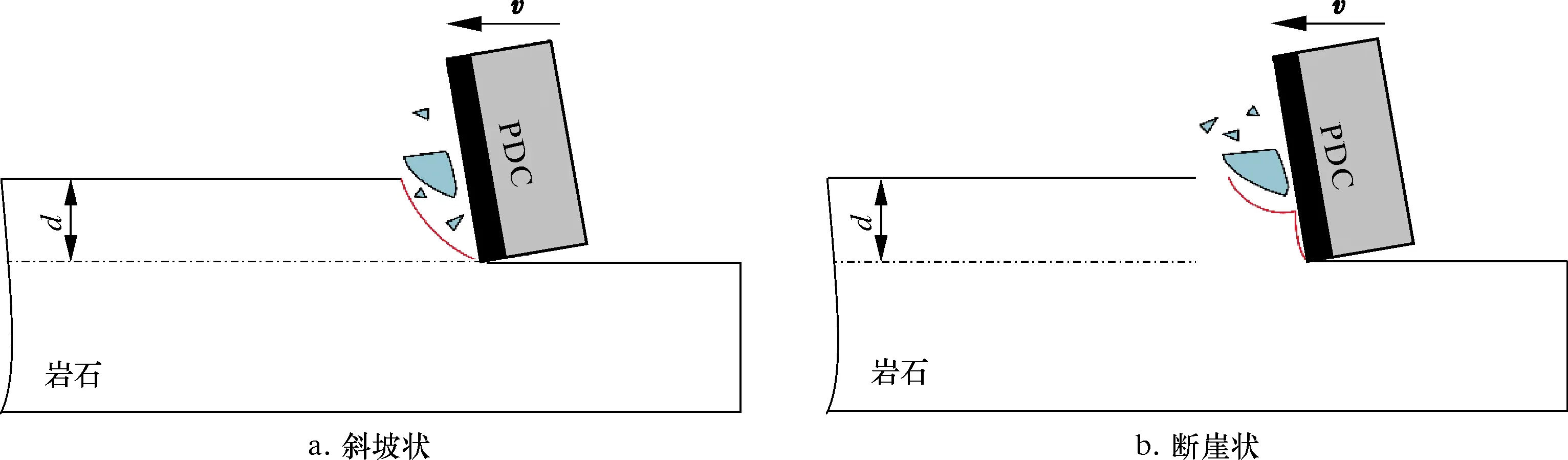
图9 前刀面与岩石的不同接触情况Fig.9 Different situation of contact between front cutter and rock
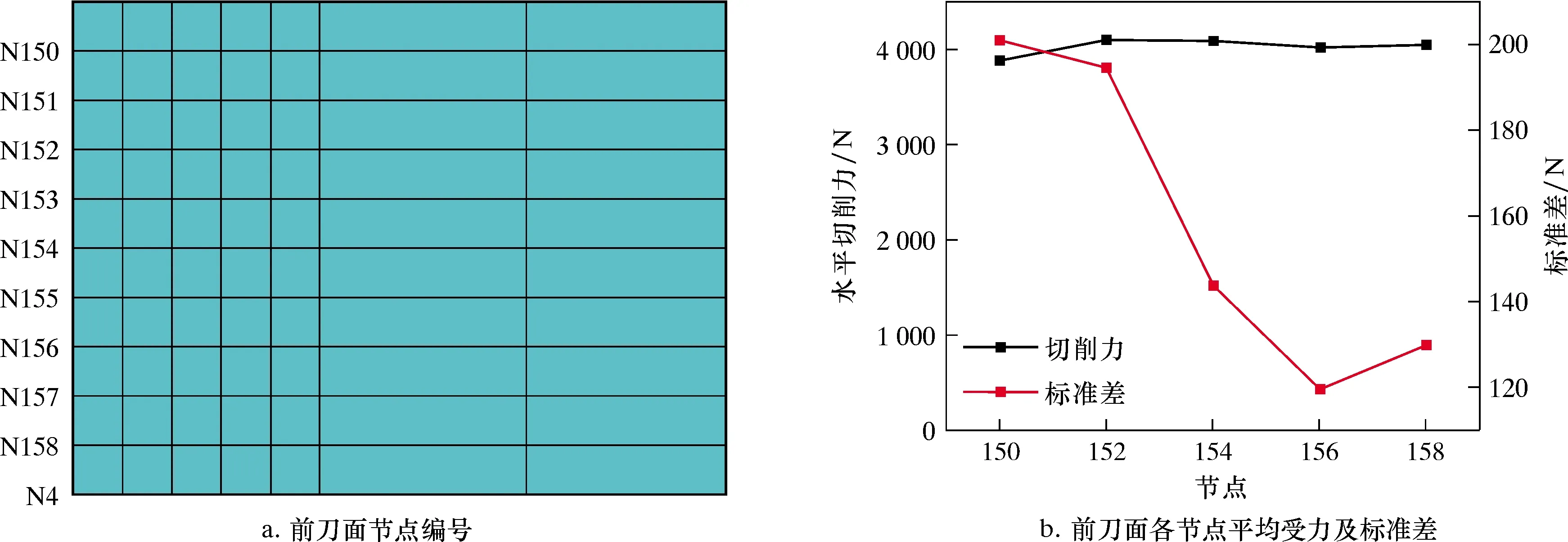
图10 d=1.8 mm时PDC切削齿前刀面各节点的受力示意图Fig.10 Forces acting on the nodes of the front PDC cutter with d=1.8 mm
3.2 PDC切削齿超高速碎岩机理分析
通过前述对EMS、Fcs以及切屑形成机理的分析,发现在超高速(v=13 m/s)条件下,切削深度仍然是影响岩石破碎模式的重要因素。在超高速条件下存在两个临界切削深度dcr1和dcr2,使得岩石的主要破坏模式发生两度转变。根据前述分析,PDC切削齿超高速切削过程中破岩机理如图11所示,具体分析如下。
当d 图11 超高速切削过程中3个不同阶段的 破岩机理示意图Fig.11 Schematic diagram of rock breaking mechanism at three different stages at ultra-high speed 当dcr1 当d>dcr2(阶段Ⅲ)时,岩石裂纹萌生和扩展机制发生了一定改变,导致裂纹产生的条件更加苛刻,脆性切削作用减弱。除此之外,岩石更倾向于从刀具与岩石接触面中部断裂,有效切削深度减小,Fcs保持在较高水平且呈线性增加,刀具压碎作用加剧,岩石塑性破坏再次占据主导地位,EMS缓慢上升,如图11c所示。 在超高速切削过程中,岩石裂纹萌生和扩展机理如图12所示。高速运动的刀具与岩石接触,在前刀面和刀尖周围产生的塑性区,分别为顶端破碎区和塑性流动区。当顶端破碎区沿着切削速度方向移动时,由于楔入效应,在顶端破碎区边界上容易萌生裂纹,并沿着弧形路径扩展至原始岩石自由表面,切屑由沿着岩石变形区域和原始岩石之间的裂纹传播路径的拉应力形成,如图12a所示。当前方岩石自由表面处形成硬化区时,未切削岩石由于惯性,来不及发生剪切滑移和沿前刀面的流动,从而在自由表面处形成裂纹,随后裂纹沿着一定角度向刀尖处扩展,形成切屑,如图12b所示。 图12 岩石裂纹萌生和扩展机理Fig.12 Mechanism of rock crack initiation and propagation 为进一步解析超高速条件下钻头与岩石之间的相互作用,本文通过有限元分析方法对PDC切削齿超高速破岩过程进行了分析,揭示了切削深度对超高速PDC切削齿破岩机理的影响规律,其主要结论如下。 (1)以EMS作为评价指标,对超高速条件下PDC刀具的切削效率进行分析。分析结果表明,当切削速度v=13 m/s时,随着切削深度的增大,EMS首先迅速降低,随后缓慢上升。PDC钻头切削齿最佳切削深度为1.4 mm,其EMS最小,切削效率最高。 (2)切削力Fcs的分析表明,存在两个临界切削深度dcr1(1.2 mm)、dcr2(1.4 mm)。随着切削深度的增大,岩石的主要失效形式由塑性破坏逐渐转变为脆性破坏。与常规切削速度不同的是,当d>dcr2(1.4 mm)时,岩石脆性破坏再度占据主导地位。此时岩石更加难以萌生裂纹,脆性破坏减弱;冲击载荷较大,有效切削深度减小,塑性破坏增强。因此,在超高速破岩过程中,切削深度在1.2 ~1.4 mm之间时,切削效率较高。 (3)切屑形成机理分析表明,在超高速切削过程中,岩石裂纹萌生方式有两种。其一,裂纹在顶端破碎区边界上产生;其二,由于材料硬化而在岩石自由表面处萌生裂纹。另外,由于岩石断裂位置的不同,切削过程中的有效切削深度会减小。 (4)在超高速切削过程中,岩石的破碎方式与切削深度息息相关。本文的研究结果为以后深入研究岩石材料特性以及其他切削参数(后倾角等)对超高速钻进的影响奠定了基础。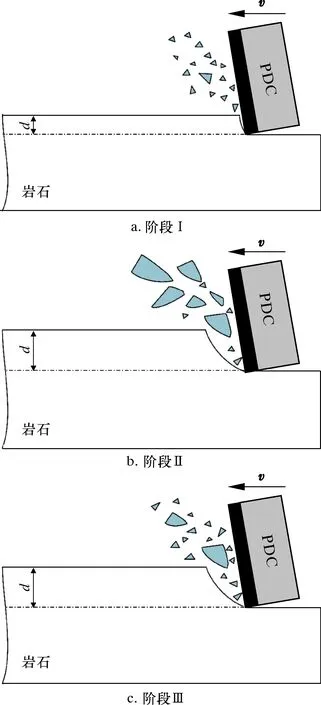
4 结 论

