基于多模态信息融合的水下移动目标定位
刘树东,梁婷蓉,王 燕,张 艳
(天津城建大学 计算机与信息工程学院,天津 300384)
0 引言
水下无线传感器网络(underwater wireless sensor networks, UWSNs)在海洋资源勘探、水下军事监视、海洋环境监测、地震海啸预警等领域具有广泛的应用。基于UWSNs的潜艇、水下无人潜航器等水下航行器可进入目标海域进行侦测,此过程中它们的位置和速度信息发挥着重要作用。因此,对水下移动目标精准定位的研究有着重要的作用及意义。
水下移动目标定位主要通过观测量信息进行定位。信息类型有到达时间(time of arrival,TOA)、到达时间差(time difference of arrival, TDOA)、到达角(angel of arrival, AOA)、到达频率差(frequency difference of arrival, FDOA)、接收信号强度(received signal strength indicator, RSSI)等。但在一些复杂定位场景中,基于单个观测量的单一模态信息无法满足定位精度要求,所以很多学者研究通过融合不同模态类型观测量信息定位以提高定位精度,主要有以下两种:TDOA/FDOA和TDOA/AOA。理论上在具有相同传感器数量时,相比于2个观测量双模态信息融合的定位方式,3个观测量多模态信息融合定位对移动目标位置和速度信息有更高的估计精度。
目前定位的主要挑战为定位系统方程的非线性问题。研究者针对非线性位置方程提出泰勒算法,但此算法需要较准确的初始值且收敛性不确定。为解决上述问题,文献[9]提出基于两步加权最小二乘(two-step weighted least squares,TSWLS)的TDOA/FDOA联合定位的经典定位算法。以 TSWLS为框架,文献[10]在文献[9]的基础上考虑了传感器位置误差,并且与无传感器位置误差情况中的克拉美罗下界(cramer-rao lower bound,CRLB)比较;文献[12]提出基于自适应TDOA和AOA联合定位算法,由于其TDOA观测量方程在两阶段定位算法中的自适应性,与文献[13]中传统TDOA/AOA联合定位相比,定位精度有所提高,但是此方法只能估计移动目标的位置信息,无法估计其速度信息;另外,文献[14]虽融合了TDOA/FDOA/AOA多模态信息定位,可以同时估计目标位置及速度,但其与上述文献相同,均为借助TSWLS框架,通过引入辅助参数将非线性系统方程转换为伪线性方程求解目标状态。此类方法存在噪声小时估计精度高,噪声较大时估计精度低,适应测量噪声能力较差的问题。
针对上述问题,本文提出一种基于 TDOA/FDOA/AOA多模态信息融合的三步定位算法。为充分利用多模态信息,算法前两步融合移动目标声信号到达不同传感器的时间差、频移差及角度信息建立非线性位置方程组,通过经典TSWLS估计移动目标状态信息。为更好地求解非线性位置方程组,弥补TSWLS框架噪声大时估计精度低的缺陷,算法第三步将定位问题转换为最大似然问题,引入鲸鱼优化算法对移动目标的位置和速度信息进行优化。优化过程中,算法第三步在前两步的基础上构造目标状态的初始种群,且将固定种群范围变为动态;设计含有不同观测量测量误差方差倒数权重信息的种群适应度函数,增加寻找最优目标的可能性。仿真实验表明,本文所提算法在一定噪声条件下可以达到 CRLB且能够更好适应测量噪声。
1 定位模型
本文基于水下传感网络的定位模型如图1所示。

图1 定位模型
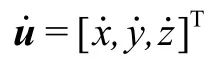


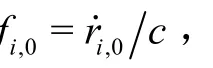


假设目标辐射信号到达第+1个传感器节点的方位角和俯仰角分别为θ和 φ(= 0,1, … ,−1),根据图1中目标与传感器节点之间的位置关系,所测方位角和俯仰角可分别表示为

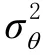
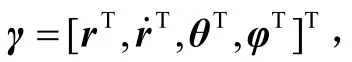
2 基于TDOA/FDOA/AOA多模态信息融合定位算法
本节具体给出基于TDOA/FDOA/AOA多模态信息融合定位算法的推导过程。该算法分为三步,前两步遵循TSWLS框架求解定位问题;第三步将定位问题转化为最大似然问题,实现位置及速度解的优化。
2.1 第一步,加权最小二乘法



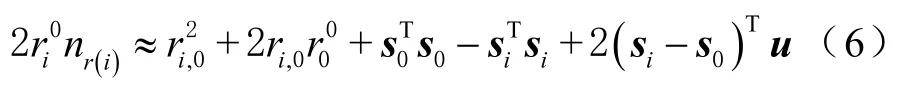
对式(5)求时间导数,可将FDOA信息方程线性化,其结果为



将式(6)和式(8)整理成矩阵形式为

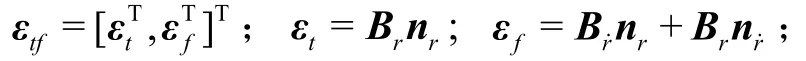

为零矩阵。
根据式(3)和式(4)可得,关于方位角和俯仰角的真实值公式可变形为

由文献[12]及图1中相应的三角形关系,将式(11)变换为






将式(15)和式(16)写成矩阵形式为

结合式(9)和式(17),基于 TDOA/FDOA/AOA多模态信息融合的定位方程可以写为

定位第一步的加权最小二乘解为

由于实际定位过程中,式(19)中的加权矩阵未知,所以先令=,得到移动目标估计值,然后利用初始估计值更新加权矩阵,从而得到更准确的估计值。表达式为


2.2 第二步,考虑约束关系的加权最小二乘法



式(21)的加权最小二乘解为

式中:为第二步加权矩阵,若使的估计方差最小,其最优选取为


则第二步目标位置和速度估计为

式中:=diag{sgin ((1 :3)-)}。
2.3 第三步,最大似然法
由于算法前两步在求解非线性位置方程过程中,为增加可靠性加入TDOA、FDOA、AOA三个观测量的测量误差即噪声项,但此操作在噪声较大时,会严重影响算法的估计精度。所以算法第三步,利用最大似然法重新表述定位问题进行求解,减少大噪声对算法估计精度的影响。

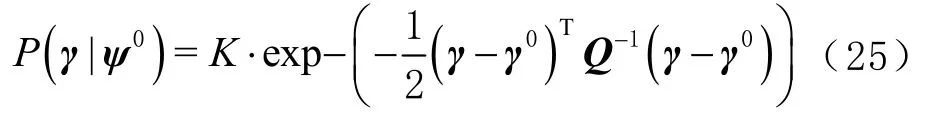
式中,表示常数。移动目标位置和速度参数的似然函数可以表示为
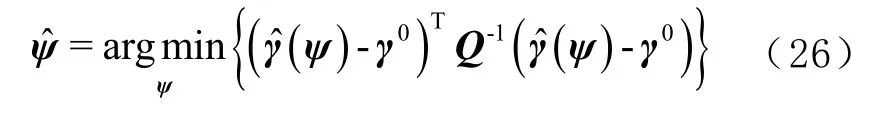
因为式(26)是非线性方程,无法得到解析解,所以本文采用改进鲸鱼优化算法进行求解。在实际定位中真实向量未知,所以用观测量代替。为了提高本文定位算法在噪声较大时的估计精度,增强算法适应测量噪声的能力,设计算法的适应度函数为

式中:

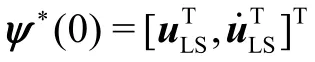
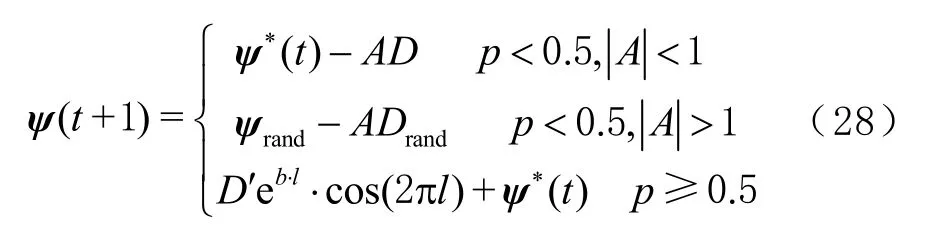

当<0.5时,随着值的减小,的变化范围也在不断缩小。当的值在区间[−1,1]上时,通过减小当前位置和目标最优位置之间的距离,从而靠近最优目标位置;当的值不在区间[−1,1]上时,随机选择一个位置,缩小随机位置和当前位置之间的距离更新,从而实现对搜索范围的缩小。当≥0.5时,根据当前位置和最优位置之间的距离,在二者之间建立一个螺旋方程使当前位置螺旋移动更新。采用上述三种方式进行位置更新,直到达到最大迭代次数,则当前最优位置为最终目标估计位置。
3 仿真实验
本节考虑两个仿真场景,通过仿真实验评估本文算法的定位性能。场景1为使用6个传感器节点对传感器区域内目标进行定位;场景2为使用6个传感器节点对传感器区域外目标定位,两个场景中传感器节点均随机分布在1 000 m×1 000 m×500 m的三维空间内。上述两个场景中的传感器区域、目标位置及其运动轨迹的二维平面示意图如图2所示,虚线框表示传感器区域,6个传感器节点随机分布在传感器区域内,场景 1中的目标及其运动轨迹处于传感器区域内,而场景 2中的目标及其运动轨迹处于传感器区域外。

图2 定位场景二维平面示意图



推导本文所提算法估计目标误差的CRLB为

式中:


3.1 目标位于传感器区域内的仿真实验
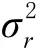

图3 目标位于场景1时的位置RMSE曲线

图4 目标位于场景1时的速度RMSE曲线
图5和图6是本文算法及其对比算法估计位于传感器区域内目标的 bias曲线。由图5可知,当总体测量误差 1 0lg()≤10 dB 时,就位置偏差而言,文献[6]算法的表现要优于其他算法,文献[6]算法表现方差较高,偏差较低,这是由于该算法不同于其他算法,算法增加了牛顿迭代。图5中当 1 0lg()≤-10 dB时,本文算法及对比算法的10lg(b ias)均小于0,即bias小于1m,所以相对于水下定位,不同算法估计位置的性能相差不大。当 1 0lg()≥0时,本文算法的偏差最小。由图6实验结果可知,对传感器区域内的目标进行速度估计时,本文算法估计偏差小于TSWLS算法。

图5 目标位于场景1时的位置bias曲线

图6 目标位于场景1时的速度bias曲线
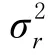
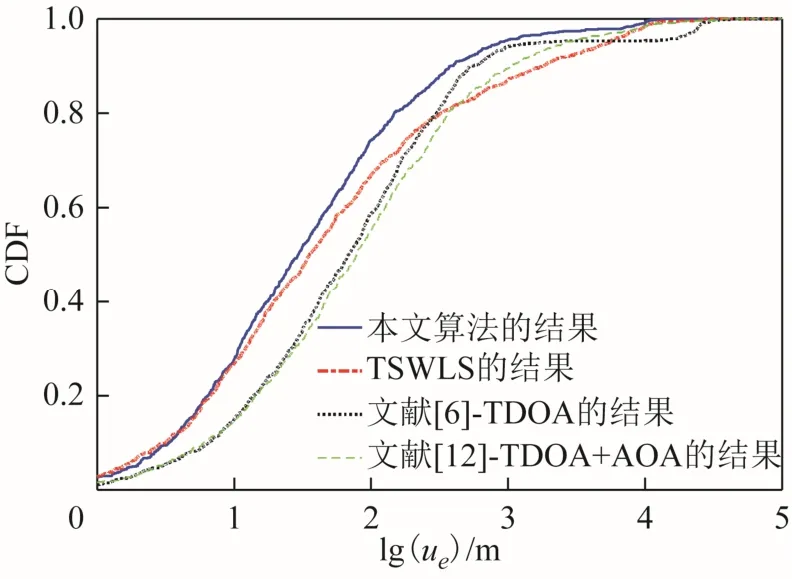
图7 目标位于场景1时的位置估计CDF曲线

图8 目标位于场景1时的速度估计CDF曲线
3.2 目标位于传感器区域外的仿真实验


图9 目标位于场景2时的位置RMSE曲线

图10 目标位于场景1时的速度RMSE曲线
图11和图12是本文算法及其对比算法估计位于传感器区域外目标的bias曲线。由图11可知,当总体测量误差 1 0lg()≤-30 d B 时,本文算法及对比算法的10lg(bias)均小于0,即bias小于1 m。当 1 0lg()>-10 d B时,本文算法偏差最小,表现最优,文献[6]算法次之,TSWLS最差。

图11 目标位于场景2时的位置bias曲线

图12 目标位于场景2时的速度bias曲线

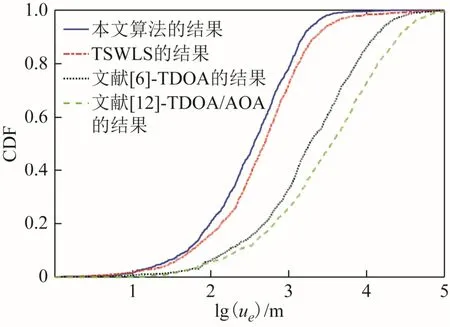
图13 目标位于场景2时的位置估计CDF曲线

图14 目标位于场景2时的速度估计CDF曲线
3.3 传感器节点数目对估计精度的影响


图15 不同算法估计位置RMSE随传感器节点数变化情况

图16 不同算法估计速度RMSE随传感器节点数变化情况
3.4 WOA算法、FDOA信息以及AOA信息对定位性能的影响
为了验证WOA算法、FDOA信息以及 AOA信息对定位性能的影响,在仿真场景 1中采用控制变量的思想,将本文所提算法与分别去除WOA算法、去除FDOA信息、去除AOA信息的算法相比较,本文算法及其去除不同信息后估计位置和速度的RMSE曲线如图17和图18所示。由图17和图18可知,本文算法要优于去除WOA算法或任何一种观测量信息的算法,这表明WOA算法及其他观测量的加入对本文算法估计目标位置及速度性能的提升具有积极作用。

图17 本文算法及其去除不同信息后估计位置的RMSE曲线
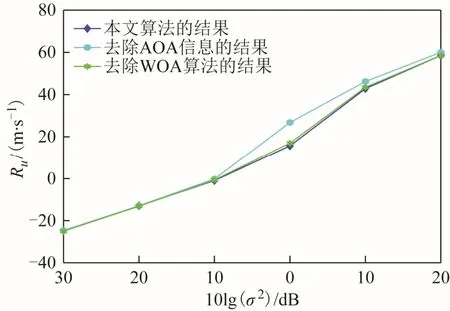
图18 本文算法及其去除不同信息后估计速度的RMSE曲线
本文算法及其去除不同信息后估计位置和速度的bias曲线,如图19和图20所示。由图19可知,与去除任何一种观测量信息或WOA的算法相比,本文算法估计位置的 bias曲线呈现出较大优势,本文算法的定位性能较好。由图20可知,本文算法速度估计 bias曲线不稳定,在某些噪声情况下估计速度的bias值要大于去除AOA信息和去除 WOA算法的 bias值。但是从纵坐标轴的取值看,在10lg()小于等于0时,三者之间的差距较小,小于1 m。总体上,由包含不同信息算法估计位置及速度的RMSE和bias曲线可知,本文算法要优于分别去除WOA算法、去除FDOA信息、去除AOA信息的算法。

图19 本文算法及其去除不同信息后估计位置的bias曲线
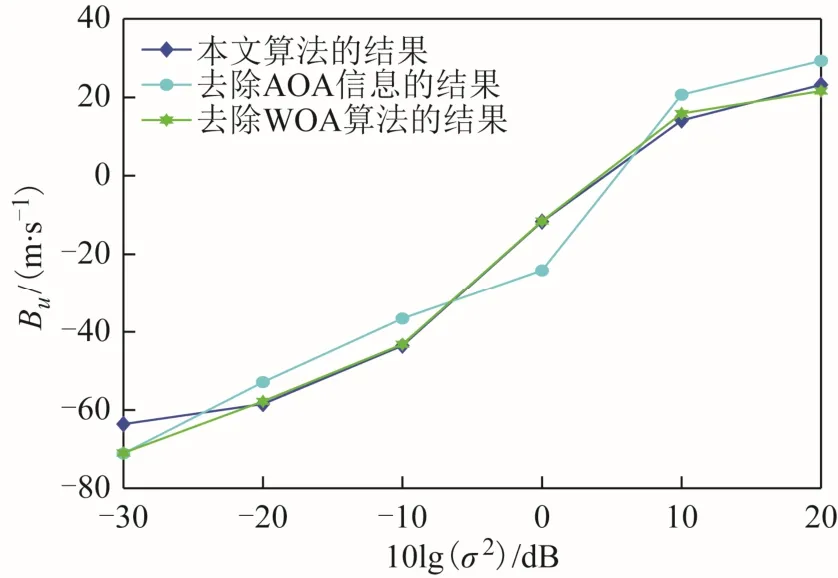
图20 本文算法及其去除不同信息后估计速度的bias曲线
4 结束语
本文提出了一种基于 TDOA/FDOA/AOA多模态信息融合的三步定位法,该算法可以同时对移动目标位置及速度进行估计。算法首先利用两步加权最小二乘法获得移动目标参数信息;然后通过推导将问题转化为最大似然函数估计问题,引入鲸鱼优化算法,将包含目标位置和速度的种群适应度函数与测量噪声方差相联系,来提高估计精度。通过对传感器区域内外的移动目标仿真实验证明,本文算法相对于其他算法目标参数估计精度高,且对系统测量噪声具有良好的适应能力。但是在实际情形中,由于海水的流动性,传感器会存在位置误差,下一步将考虑传感器位置误差进行仿真实验。

