DGMM加权混合滤波RSSI室内定位算法

张永恒，陈红华,2，郭 语，聂舜启

（1.南京林业大学 土木工程学院，南京 210037；2.东华理工大学 江西省数字国土重点实验室 南昌 330013）

0 引言

基于无线传感网络的室内定位主要包括测距定位和非测距定位。其中，测距定位模型主要有接收信号强度指示（received signal strength indicator, RSSI）、到达时间（time of arrival,TOA）、达到角（angle of arrival, AOA）和到达时间差（time difference of arrival, TDOA）等；非测距算法主要包括质心算法等。基于RSSI定位方法具有硬件成本低、定位精度相对较高、硬件便于部署等优点，因此仍为解决室内定位精度问题研究的重点。

基于RSSI室内定位技术重点研究测距模型和定位算法。针对测距模型，文献[7]通过模型参数、锚节点选取、节点升级和未知节点坐标估计动态修正测距模型，虽然测距精度有一定程度提高，但该方法没有考虑RSSI异常值不严格服从高斯分布对滤波结果产生的影响；文献[8]利用蚁群算法获取最优的初始阈值和权值，并将其赋予反向传播（back propagation, BP）神经网络拟合定位，此方法虽然提高了定位精度，但需要在室内环境中获取大量训练样本。针对定位算法，文献[9]提出通过构建相交圆计算质心位置，利用参考质心计算修改因子修正其余质心，最终用加权修正后的质心计算坐标，此方法在通信半径30 m以内的定位精度与稳定性，相对于其他算法更加突出，但此方法易受测距模型参数误差影响，且无线信号不严格服从高斯分布。

针对RSSI信号会出现波动的异常值，且定位精度受测距模型参数拟合的影响，本文提出了狄克逊检验法高斯均值中值（Dixon Gaussian median mean,DGMM）加权混合滤波 RSSI值进行高斯牛顿定位，极大地提高了定位精度以及稳定性，有较强的实用性。

1 RSSI测距模型

无线信号在传播过程中受距离和室内环境的影响会产生损耗。因此可以利用损耗这一特征，分析信号穿透物体的能力，建立信号损耗和距离之间的映射关系。常用的对数衰减模型为

式中为信号传输过程中的损耗值；为目标点距已知蓝牙信标点一米处的信号损耗值；为目标点至蓝牙标签之间的距离；为衰减因子，不同的场景，衰减因子取值不同；为穿透建筑物的损耗，在实际计算中忽略不计。故信号接收端至发射端的距离可由式（1）化简为

由公式（2）可看出，RSSI值的精度影响蓝牙标签至目标点的测距精度，并进一步影响定位精度，故如何处理RSSI并提高其精度是接下来研究的重点。

2 DGMM加权混合滤波

2.1 狄克逊检验

基于RSSI定位精度取决于信号值样本好坏和测距模型参数的精确度，为提高定位精度，在加权混合滤波前需通过狄克逊检验法预处理，剔除RSSI异常值，得到近似高斯分布的信号值。首先计算偏度大小，判断信号的分布，再利用数据中的最值计算极差比来判断波动的信号值的峰值是否为异常值。

偏度可用来描述统计数据分布的对称程度。一组RSSI观测数据的偏度可表示为

式中：为偏度；为RSSI值；为RSSI值的期望为RSSI值的方差。

当偏度为0时，观测数据符合正态分布；当偏度小于0时，说明观测数据向左偏；当偏度大于0时，说明观测数据向右偏。

极差比是最接近最值的值与最值的差之比，反映最值的偏离程度。将最值作为可疑值，利用最大最小值计算极差比，最终通过假设检验剔除异常值。具体步骤如下：

①将蓝牙标签采集的信号衰减值按从小到大依次排列得<<…<r，本文将显著性水平设置为0.05，查询临界值D（0.05，）。

②根据数据量检验高端异常值和低端异常值γ为

式中：r为样本最大值；r为最接近最大值的样本值；为样本最小值；r为最接近最小值的样本值。

③若>γ，且>D（0.05，），则最大值判定为异常值；若<γ，且γ>D（0.05，）时，则最小值判定为异常值；否则认定数据中未含有异常值。

④剔除当前异常值后，重复步骤①至步骤③，直至未发现异常值。

2.2 GMM加权混合滤波

由于单一的滤波无法对RSSI信号进行最优化处理，本文提出了一种改进的混合滤波算法，将预处理后的数据进行高斯滤波处理，再分别进行中值滤波和均值滤波处理，最后加权得到理想的RSSI值。具体步骤如下：

①对狄克逊检验法预处理后的数据进行高斯滤波，得到过滤后的个RSSI序列，记作R。

②对得到的 RSSI序列按从小到大顺序R，R，…，R重新排序。计算当前序列的算术平均值和中间值。

③将各RSSI值与均值和中间值的偏差平方均值作为各自的阈值，若偏差平方小于阈值，则用阈值来确定权值；反之，则用偏差平方来确定权值，使权值的确定更为合理。权值计算公式为

式中，

④ 对和作 以 下 处 理 ：ω=⋅+⋅，其中=1，本文取=0.5，=0.5。将序列中的每个 RSSI值与加权权重ω相乘后得校正后的RSSI值为

基于DGMM的加权混合滤波算法结合了现有滤波算法的优点，能够有效过滤多种因素干扰，从而得到最理想的RSSI值。

获取精度较高的RSSI值后，通过测距模型可得到蓝牙标签至目标点之间较准确的距离，则需要进一步探究合适的距离定位模型。

3 高斯牛顿定位模型

高斯牛顿迭代法为非线性最小二乘的一种迭代方法，该方法使用一阶泰勒展开式、近似代替非线性方程，然后通过多次迭代，使原模型的残差平方和达到最小。

在室内均匀放置（>4）个蓝牙信号标签和个目标点，并建立独立的室内坐标系，将蓝牙信标放置在已知位置。将蓝牙标签坐标记为A=（a，b），（=1,2,…,），假设第个目标点的坐标为T=（x，y），（=1,2,…,），将加权混合滤波处理后的RSSI值代入式（2），得蓝牙标签到目标点距离为d，则可得该目标点观测方程为

令=3，由三边定位法计算目标点的初始坐标。在目标点初始坐标处对非线性误差方程式（8）进行线性化，使用泰勒级数展开式、近似代替非线性回归模型，不断迭代修正方程参数使得残差平方和最小。展开后的线性方程为

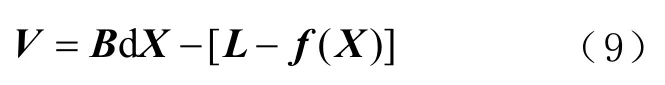
式中：为()对的雅克比矩阵，即

在=处，对式（9）中的求微分，由最小二乘原理解得

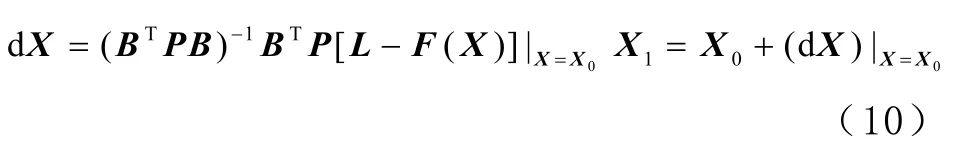
式中，为权阵。

权阵的计算方法为

式中：ω为权重；R为加权混合滤波处理后的信号衰减值。

以为近似值继续迭代，其公式为

当 ()与 ()之间差值最小时，停止迭代。

计算目标点的点位误差，其公式为

式中：为点位误差；ˆˆ、分别为目标点横纵坐标估计值；、分别为目标点横纵坐标理想值。

4 实验与分析

选择南京林业大学主楼大厅作为室内环境。此环境长15.6 m，宽6.2 m，在大厅内布设6个蓝牙标签，选择8个目标点进行定位，场景模拟图如图1所示。在室内建立独立坐标系，分别测量蓝牙标签和目标点的理想坐标，打开蓝牙标签，使用移动手机接收蓝牙信号采集RSSI值。

图1 实验场景模拟图

由于不同的室内环境衰减模型参数有差异，仍需要采集一定的样本值拟合衰减模型参数。为方便测量，选择一条长8 m的直线，每隔0.5 m采集蓝牙标签 3的信号强度衰减值。对采集的16组样本数据过滤后进行拟合，得到该环境下衰减模型参数=-58.13，=2.46。曲线拟合图如图2所示。

图2 衰减模型曲线拟合图

在实验中，分别实现中值滤波、均值滤波以及DGMM加权混合滤波对实测样本数据处理后的高斯牛顿定位。表1为 3种滤波算法处理后高斯牛顿定位结果的一维误差和点位误差。

表1 三种滤波定位算法误差对比

通过对连续观测的数据进行狄克逊检验法预处理，可有效剔除异常值，得到接近高斯分布的信号强度值。继续使用DGMM加权混合滤波，可得到相对稳定的强度值，最后进行高斯牛顿定位。实验结果的误差如表1所示，分别计算3种滤波的 DGMM加权混合滤波处理后的平均点位误差为1.523 m，精度明显优于均值滤波的4.846 m和中值滤波的 4.302 m，定位精度提高了 3倍。利用文献[13]的高斯中值混合滤波和文献[14]的加权混合滤波对本文数据进行处理得到平均点位误差分别为3.63 m和3.19 m，对比显示本文的 DGMM加权混合滤波算法的定位精度仍具有明显优势。

实验实现了对目标点均值滤波、中值滤波以及DGMM加权混合滤波算法处理后的定位，估计位置与理想位置对比如图3所示。图3显示，3种滤波算法中，DGMM加权混合滤波处理后定位的估计点位与理想点位之间的距离最小，即点位误差最小，说明此方法的定位精度最高。

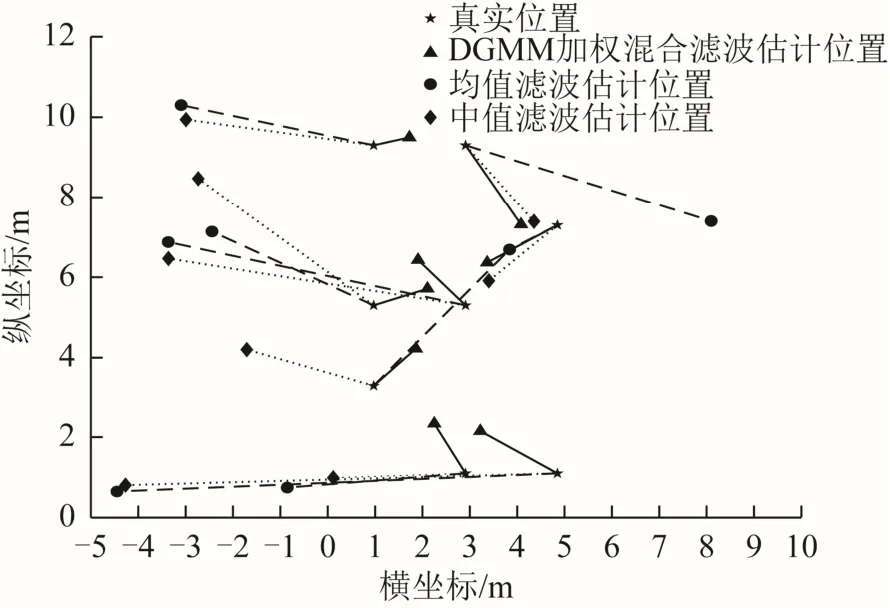
图3 三种滤波算法估计位置和理想位置

图4为3种滤波算法的点位误差示意图。从图4可看出DGMM混合滤波算法的点位误差在0~3 m，精度明显高于均值滤波和中值滤波的定位结果。对于4号点、6号点及7号点，均值滤波和中值滤波的定位误差波动较大，定位精度非常不稳定。计算均值滤波、中值滤波和DGMM加权混合滤波点位误差的均方差根误差分别为 2.212、2.273和0.441 m，其中DGMM加权混合滤波点位误差的均方差根误差最小，说明其定位的点位误差波动范围最小，即定位最稳定。

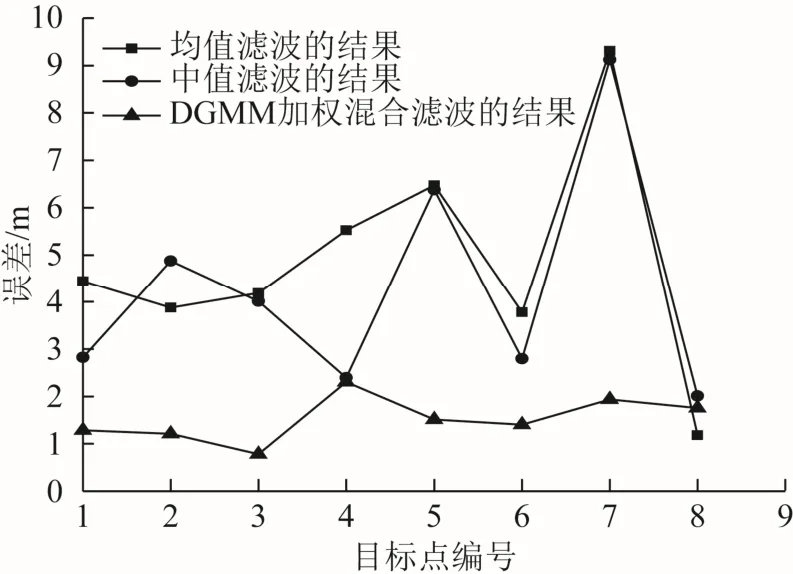
图4 点位误差

为了进一步研究高斯牛顿定位模型的优越性，将同样的一组 DGMM 加权滤波处理后的RSSI值代入式（2），计算蓝牙标签到目标点的距离后，利用最小二乘线性化定位模型进行位置估计，与本文的高斯牛顿定位模型进行对比。表2为最小二乘定位和高斯牛顿定位结果的一维误差和点位误差。

表2 两种定位模型误差对比

定位误差如表2所示。分别计算两种定位模型的平均点位误差，最小二乘定位模型的平均点位误差约为2.737 m，高斯牛顿定位模型的平均点位误差约为1.523 m，所以本文采用的定位模型精度提高了79.7%，明显优于最小二乘定位模型。

图5为两种定位模型的误差示意图。从图5可看出，虽然最小二乘定位模型 1号点位定位精度优于高斯牛顿定位，是由于最小二乘线性化求解坐标定位很不稳定，会出现极个别定位精度较好的情况，但高斯牛顿定位模型总体定位精度较高且比较稳定，误差维持在0~3 m。

图5 点位误差

综上所述，实验结果表明，DGMM加权混合滤波后的 RSSI值利用不同的定位模型定位精度，都优于均值滤波和中值滤波。进一步研究发现，本文采用的高斯牛顿定位模型，进一步将定位精度提高了79.7%。故利用DGMM加权混合滤波处理RSSI的高斯牛顿模型，可大大提高室内定位精度。

5 结束语

针对基于RSSI的室内定位方法采集的信号衰减值会出现波动的异常值等问题，本文首先使用狄克逊检验法逐步剔除异常值，再对符合高斯分布的数据值进行高斯滤波，并分别进行均值滤波和中值滤波，对两种滤波处理后的结果进行加权处理，最后使用高斯牛顿模型迭代得到最优的估计位置。实验结果表明，本文的DGMM加权混合滤波可有效避免部分异常值对滤波结果的影响；选择RSSI的平方和倒数确定权，避免了使用距离确定权引起的参数误差；同时利用高斯牛顿模型能够不断修正目标点的点位误差，最终提高定位精度。但本文研究对象为静态目标点，不适用于解决动态轨迹问题，如何解决动态室内定位有待下一步研究。