高精密轧机支承辊辊系动力特性有限元法分析
王煜 闫成琨 王婉晴 谢犁 王果 马彦芝
(中国重型机械研究院股份公司 陕西 西安 710032)
1 前言
高精密轧机在轧制生产过程中,支承辊辊系处于复杂的应力状态。如果支承辊辊系的选材、设计、制作工艺等不合理,或轧制时卡钢等造成局部发热引起热冲击等,都易使支承辊疲劳失效[1]。轧辊的尺寸结构、材质、使用在相当程度上决定了轧机的技术水平,此外随着轧制技术的发展,支承辊的工作环境也越来越苛刻。辊系轴承是影响支承辊辊系单元动态特性最主要的部件[2]。角接触球轴承、圆锥滚子轴承及圆柱滚子轴承等均可用作支承辊辊系的支撑,角接触球轴承因其高速、高精度、高刚度、长寿命及能同时承受轴向与径向载荷等特点在支承辊辊系装配单元上的应用越来越广泛[3,4],辊系轴承的动静刚度等动力学性能直接影响支承辊辊系静态和动态回转精度、抗振、温升以及速度等性能[5],高速时钢球的离心力及陀螺力矩等惯性效应导致内外圈接触角、钢球接触载荷以及接触区润滑状态发生改变,使球轴承运动状态的刚度与静止状态的刚度产生差异[6],同时,对球轴承适当的预载,消除内外圈之间的游隙,使钢球和内外圈产生弹性接触变形,可增加承载钢球的数量及使各钢球受力趋于均匀,有利于提高支承辊辊系支撑轴承的刚度、辊系单元的回转精度及抗振等性能[7,8]。
鉴于支承辊辊系单元动态特性对高精密轧机整体精度的重要性[9],在支承辊辊系单元的设计过程中对支承辊辊系单元和支撑轴承的性能及影响因素进行准确分析是保证所设计轧机的生产效率、加工精度及可靠性等性能的有力手段。对支承辊辊系单元的动态特性分析,主要有模态综合法、传递矩阵法及有限元法等方法,包括固有频率、振型的模态分析、不平衡响应及周期性外载荷作用下的谐响应分析等内容[10-12],其中,如何正确简化轴承弹性支撑是支承辊辊系单元动态分析的关键的技术难点[13-15]。
Gentle等人对纯轴向载荷作用下角接触球轴承,采用拟动力学方法对其稳态工作特性进行了理论分析,利用试验验证了润滑介质产生的拖动力模型[16]。Nelias和Sainsot等人考虑了保持架对钢球运动规律的影响,分析了球轴承的运动规律及摩擦功率损耗,建立了联合载荷作用下角接触球轴承拟动力学分析模型,通过分析得到的保持架速度与试验值吻合较好,从而验证了该模型的合理性[17]。Walters首先提出了钢球与保持架分别为四、六个自由度运动规律的动力学分析模型[18]。Gupta在此基础上详细分析了球和沟道的相互作用,推导出球轴承中各零件的运动分析式作为数学模型,开发了ADOBE程序实时分析球轴承动力学性能[19]。王黎钦建立了航空发动机高速球轴承拟动力学模型,分析了工况参数和结构参数对滚动轴承动态特性的影响规律,通过Gupta的动力学分析程序算例验证了程序的准确性[20]。蒋兴奇等对角接触球轴承进行了拟动力学分析,探讨更加符合实际的高速球轴承分析研究方法[21]。李锦标等最早采用动力学方法对滚子轴承进行了分析计算,综合考虑了滚子轴承各组件之间的作用力,得到了比较满意的分析结果[22]。
支承辊辊系单元是一种典型的加入复杂扰动的轴承转子系统[23-27],对该复杂系统动力学的主要分析方法可分为两类:传递矩阵法和有限元法。传递矩阵法具有占用计算机资源少、计算速度快及数值稳定性差等特点。
有限元法将无限自由度的连续系统简化为有限自由度的离散系统,将各种因素考虑在内的有限元模型是比较精确的模型,计算结果精度高,但是占用更多的计算机资源,若根据具体问题在不影响分析精度时,忽略不必要的非线性等因素,将非线性系统线性化将会明显提高计算效率减小计算机资源占用。随计算机的发展,有限元的建模方法使得列写乃至求解复杂精密的轴承转子结构系统运动方程成为可能。
2 辊系装配单元有限元法建模
辊系装配单元是一种典型的加入复杂扰动轴承转子系统,通常轴承转子系统可以沿轴线化分为在节点处联结的离散圆盘、分布质量的弹性轴段及轴承座等单元,单盘转子系统如图1所示。
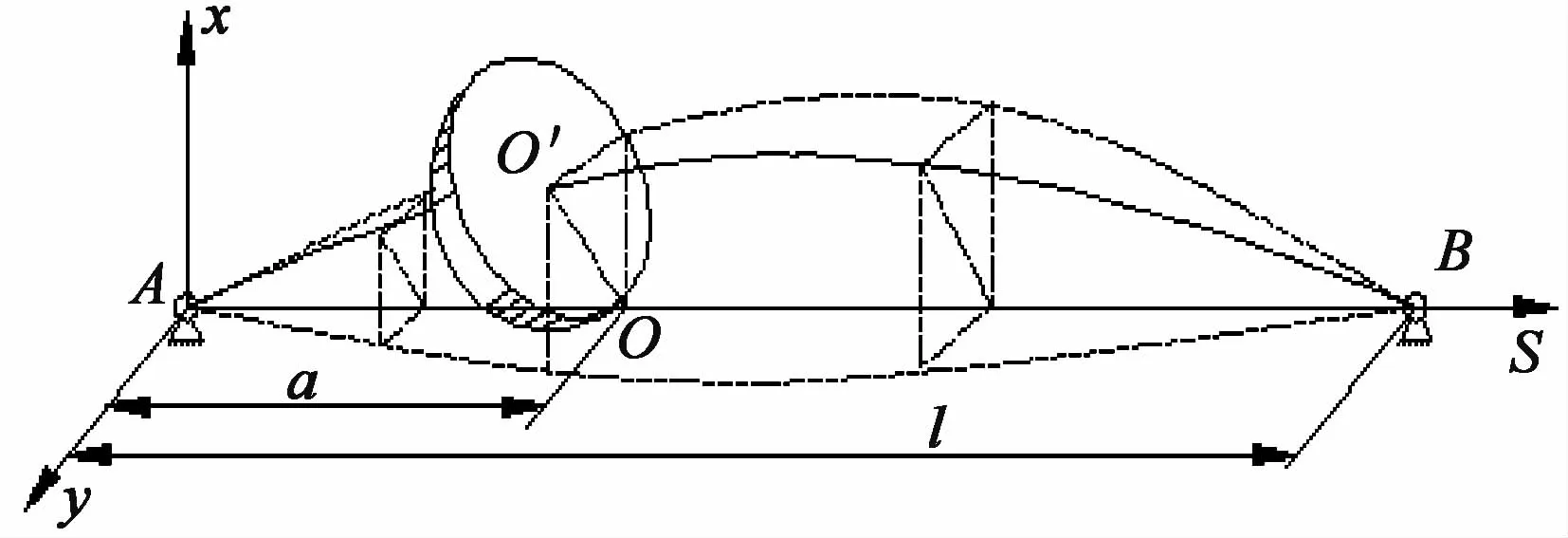
图1 单盘转子系统
若A及B位置为轴承支撑,转子轴的中心线通过圆盘中心并以等角速度Ω自转,忽略转子的扭转变形,转子的自转角φ:

以A为坐标原点,以轴承座中心线为As轴建立固定坐标系Axys,图中节点o'的坐标为(x,y),产生微小变形节点处与转子轴线垂直的横截面的偏转角为(θx,θy),在坐标系Axys中,任一横截面位移向量可描述如下:
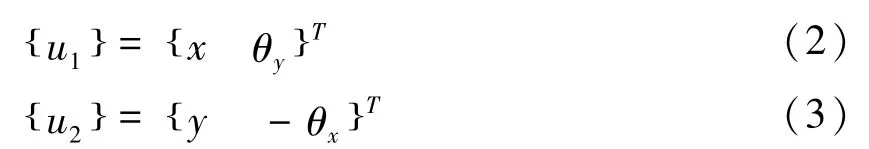
节点的位移向量定义为通过该节点且与转子轴线垂直截面的位移向量,有限元中,任一瞬时转子的位置用该单元节点的位移来表示,各节点的位移向量组成了轴承转子系统的广义坐标。分析单元节点力与位移的关系,建立单元的运动方程,以节点位移为广义坐标综合各单元的运动方程可得到系统的运动微分方程。
2.1 质量圆盘的运动方程
对于刚性圆盘,若其质量、直径转动惯量及极转动惯量分别为m、Jd和Jp。圆盘所在单元的节点位移向量为:


求得刚性圆盘的动能根据Lagrange方程可得刚性圆盘的运动微分方程:
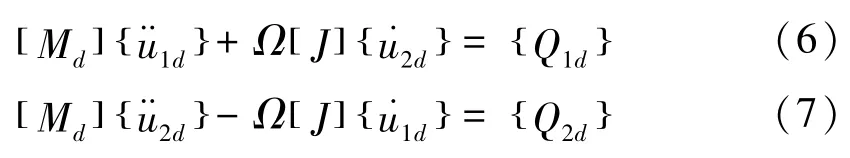
式中: Md—圆盘的质量矩阵;
Ω[J]—回转矩阵;
Q1d、Q1d—广义力。
圆盘的质量矩阵及回转矩阵如下:
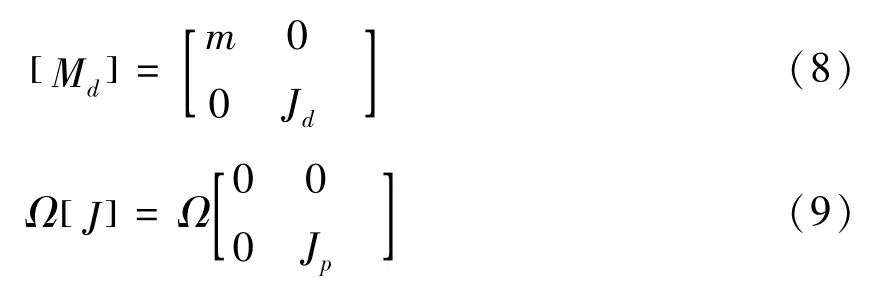
若圆盘有微小的偏心距eξ及eη,刚性圆盘的不平衡力表示成广义力为:
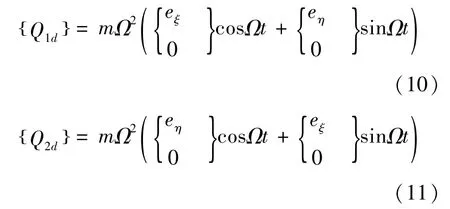
2.2 弹性轴段的运动方程
对于弹性轴段单元,如图2所示,将该单元的两端的节点位移作为其广义坐标:
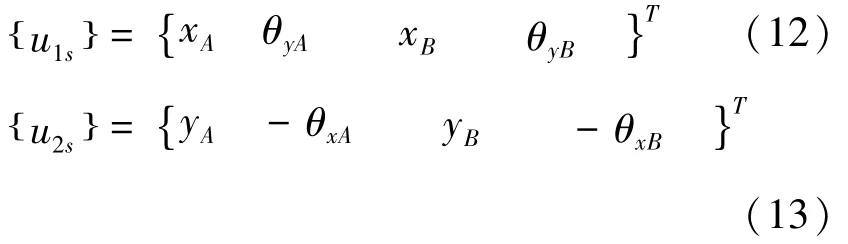
图2 弹性轴段单元
若轴段单元的单位长度质量、直径转动惯量及极转动惯量分为为μ、jd及jp,通过求得该单元的动能及Lagrange方程可得该弹性轴段的运动方程:
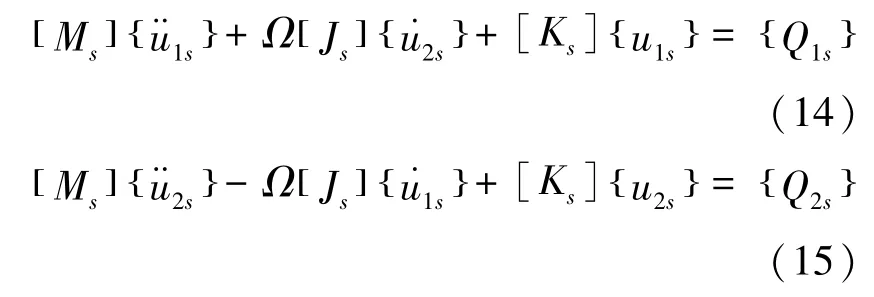
式中: Ms—质量矩阵;
Ω[Js]—回转矩阵;
Ks—刚度矩阵;
Q1s、Q1s—广义力向量。
刚度矩阵为:
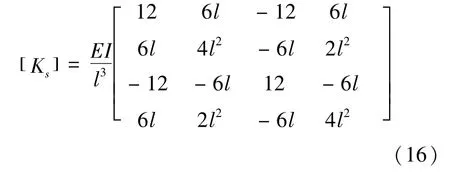
式中: EI—弹性轴段抗弯截面系数;
l—弹性轴段单元长度;
Ks—刚度矩阵。
通常,在转子动力学中将无限多个自由度质量连续分布的弹性转子系统简化为沿轴线若干个集总质量的多自由度系统,集总质量的节点一般选择在圆盘中心、轴颈中心及轴截面突变处等,如图3所示。当节点间的弹性轴段为等截面轴时,质量、直径转动惯量及极转动惯量集总如下:
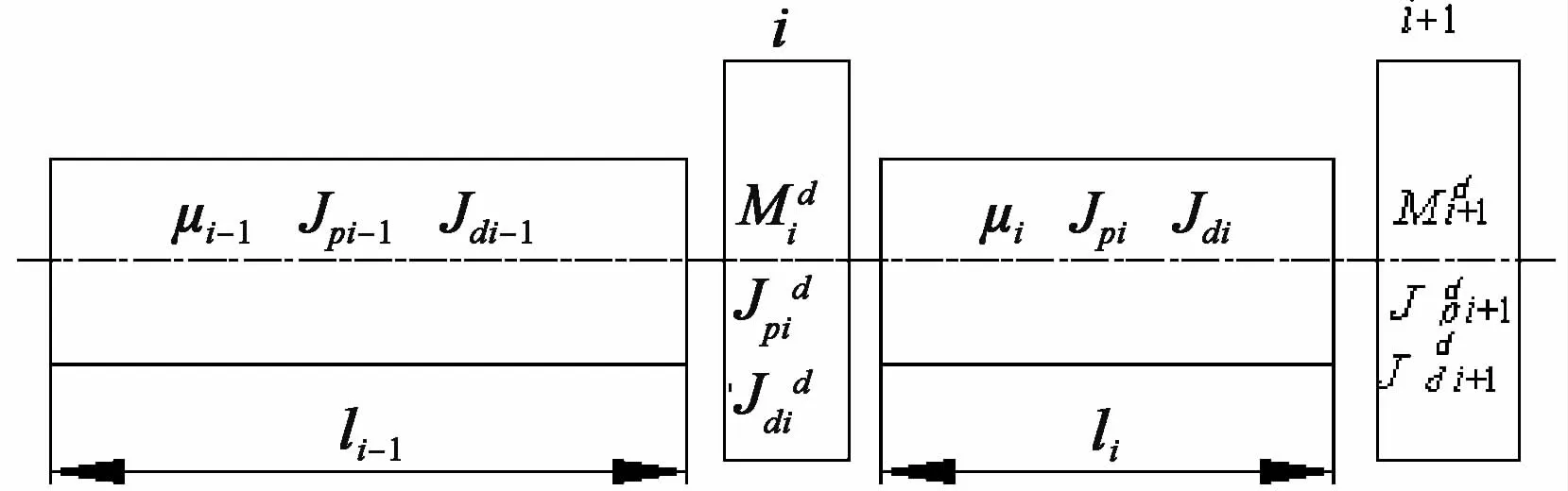
图3 转子质量离散
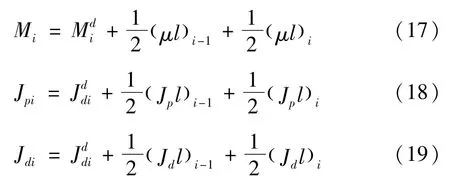
式中:Mi、Jpi、Jdi—集总到节点i处质量、极转动惯量及直径转动惯量;
μ、Jpi、Jdi—单位长度轴段的质量、极转动惯量及直径转动惯量;
l—轴段长度。
若圆盘及弹性轴段集总到A和B两点的质量、直径转动惯量及极转动惯量分别为mB、JdA、JdB、JpA及JpB,则质量矩阵、回转矩阵及刚度矩阵如下:
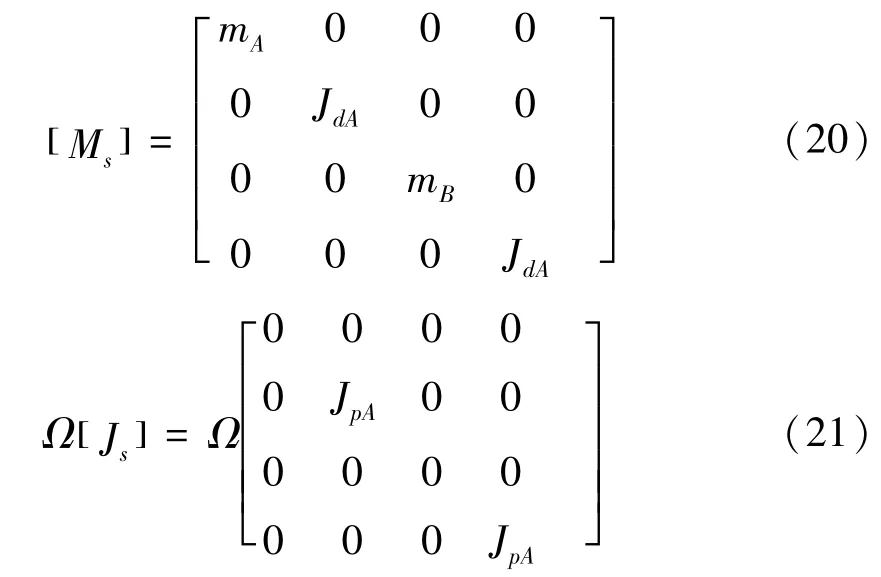
2.3 轴承座的运动方程
对于轴承座单元,将轴承—转子系统中轴承简化为弹簧支撑模型,即轴承支撑等效为阻止径向位移的线性弹簧及限制转动的扭转弹簧固定在其支承中心,如图4所示。

图4 轴承—转子支承模型原理图
若轴颈中心的编号为s(j),轴承中心及轴颈中心的坐标为(xb、yb)和(xs(j)、ys(j)),轴承座的运动方程为:
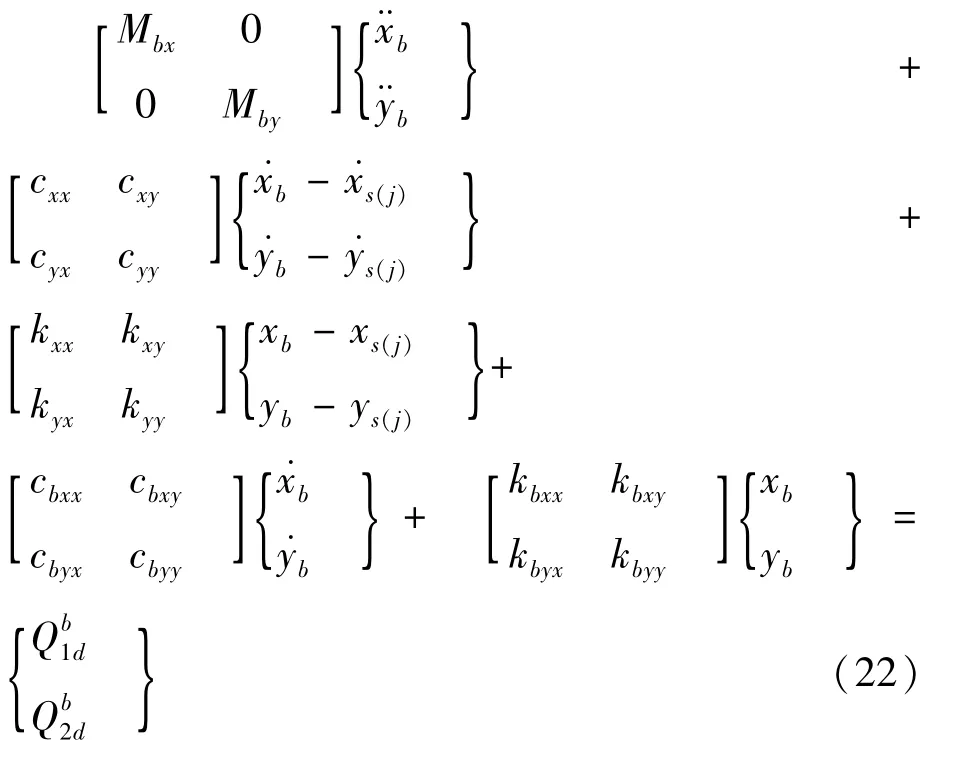
假设基础刚性较好,轴承可简化为各向同性且不计阻尼的等刚度弹性支撑,若其刚度系数为kb,其中kb与其承担的载荷有关。则轴承作用在轴颈中心的广义力为:
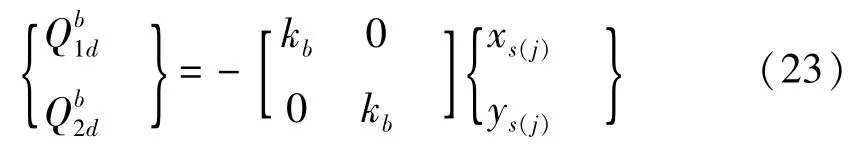
2.4 主轴单元的运动方程
将轴承转子系统划分为N个节点N-1个轴段组成的有限元模型,系统的位移向量为:

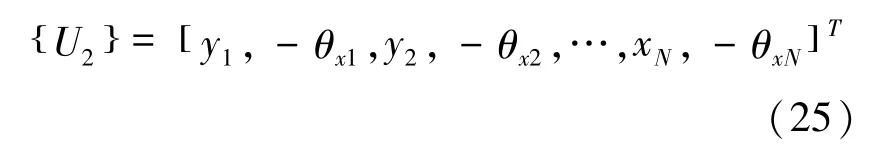
综合式(6)-(7)和式(14)-(15),即综合刚性圆盘与弹性轴段单元运动方程,将轴承的支撑广义力式(23)并入转子系统的刚度矩阵相应元素中,可得轴承转子系统的运动方程:

其中,Q不包含支承轴承反力,k为除2s(j)-1行及2s(j)-1列处为kb外,均为零的2N×2N阶矩阵,若假设:
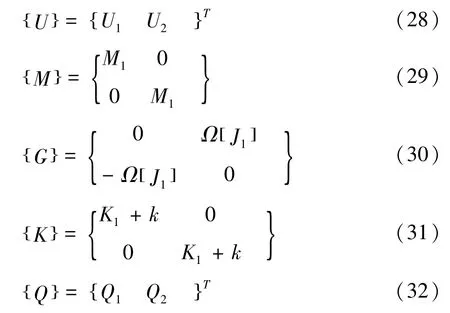
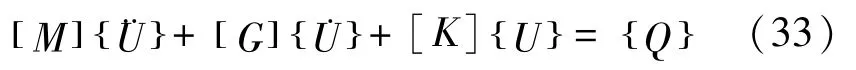
转子系统的整体质量矩阵[M1]、回转矩阵Ω[J1]及刚度矩阵[K1]均为2N×2N阶矩阵,对于整体质量矩阵[M1],将式(15)-(17)代入式(18)得到集总到节点i处质量矩阵,将其叠加到对角线上,表示圆盘及弹性轴段单元质量矩阵对整体质量矩阵的贡献。回转矩阵Ω[J1]的形成和
将式(28)-(32)代入式(26)-(27),则轴承转子系统的运动方程可表示为:整体质量矩阵的形成方法类似。对于刚度矩阵[K1]和整体质量矩阵的形成方法类似,由式(14)可得第N-1个节点与第N个节点间轴段的刚度矩阵,将对应节点处的元素叠加到对角线上。
3 辊系单元的临界转速与不平衡响应
综合转子系统圆盘、弹性轴段及轴承座等单元运动方程,建立轴承转子系统的运动微分方程,通过求解系统的运动方程的齐次解,可得转子自转角速度Ω时的涡动频率及转子的临界转速及振型,采用Newmark-β方法求解方程的稳态解可得转子系统不平衡响应。
系统的运动方程式(33)的齐次式为:
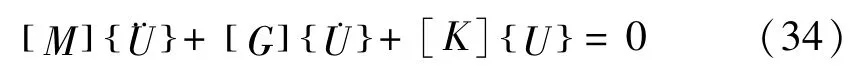
若:
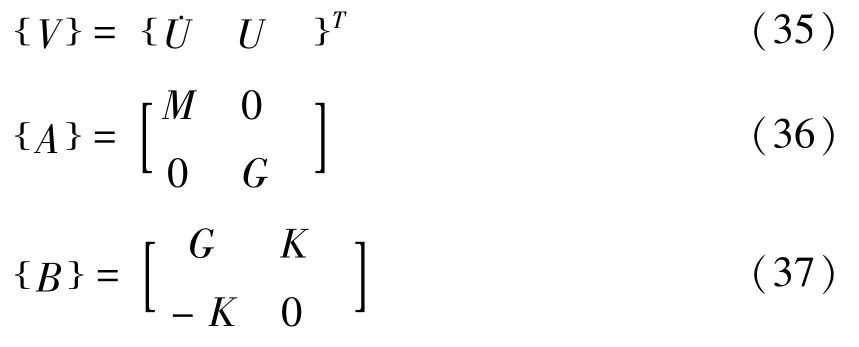
由式(35)-(37)将二阶微分方程式(34)化为8N个一阶线性方程:
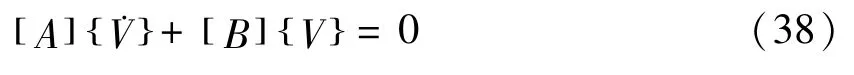
令:
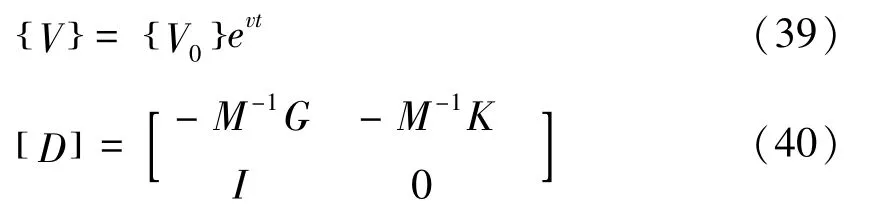
将轴承转子系统的临界转速问题转化为矩阵[D]的标准特征值v问题,即将式(39)-(40)代入式(38)可得:

矩阵[D]为8N×8N阶矩阵,其特征值是与转子的自转角速度Ω有关的成对的共轭复数,它的虚部代表自转角速度为Ω时的转子正反涡动频率。
对于自由度比较多的轴承转子系统,求解矩阵的特征值比较耗时。通常,没有必要求解出所有的特征值而只需要求解出系统的前若干阶。通过式(34),求解得转子的各种自转角速度Ω时的涡动频率ωr并将其按序排列,以自转角速度Ω为横坐标,涡动频率ωr为纵坐标,作出系列曲线,作直线Ω=±ω与曲线相交可得到轴承转子系统的同步正向涡动频率及同步反向涡动频率。由于实际转子系统不平衡质量的激励,转子作同步正向涡动,因此,转子系统的临界转速通常只考虑同步正向涡动的临界转速。
对于求得的每一阶临界转速,代入式(41),总可得8N个齐次线性方程组,令{V0}中的某元素为1,从方程组中任选(8N-1)个方程,求解其组成的方程组便可求得转子系统相应阶的主振型即模态振型,主振型上可以直观的看出不同位置相对振动幅度分布规律。
若轴承转子系统不计转轴的偏心的影响,只考虑由圆盘偏心质量引起不平衡响应,将轴承转子系统的运动方程式(33)写成如下形式:
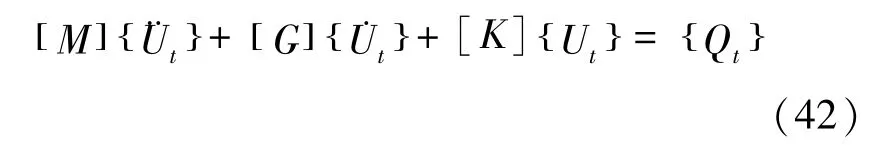
式中: ¨Ut、˙Ut、Ut—t时刻的加速度、速度及位移;
Qt—t时刻的圆盘偏心质量引起不平衡激励。
在t+Δt瞬时,由式(42)可得:
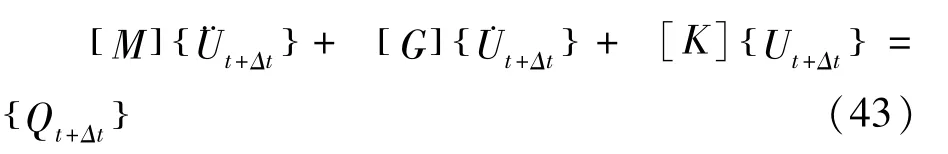
假定在时间间隔[t,t+Δt]内的加速度为:

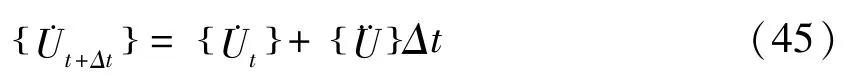
将式(44)代入式(45),可得:
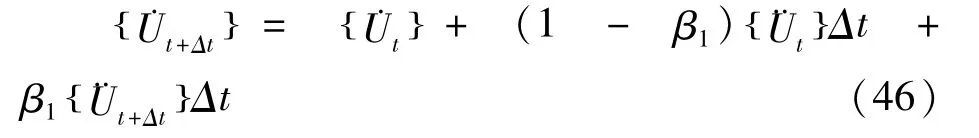
将 { Ut+Δt} 展开为二阶Taylor展开式:
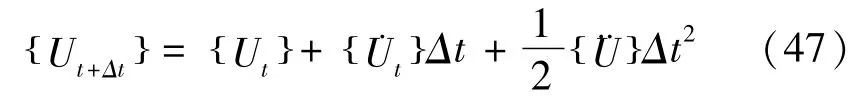
此时,又假定在时间间隔[t,t+Δt]内的加速度为:

将式(48)代入式(47),可得:
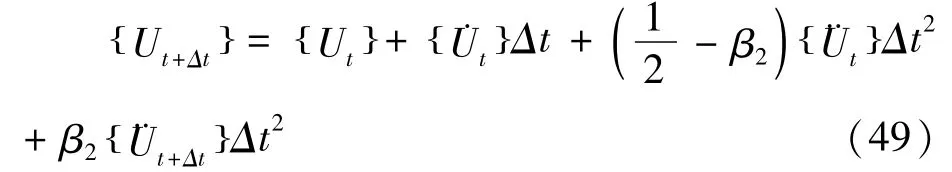
若令:
通过选择恰当的控制参数β1及β2,在已知t时刻系统的位移、速度及加速度的情况下,理论上可以求得t+Δt系统的位移、速度及加速度:
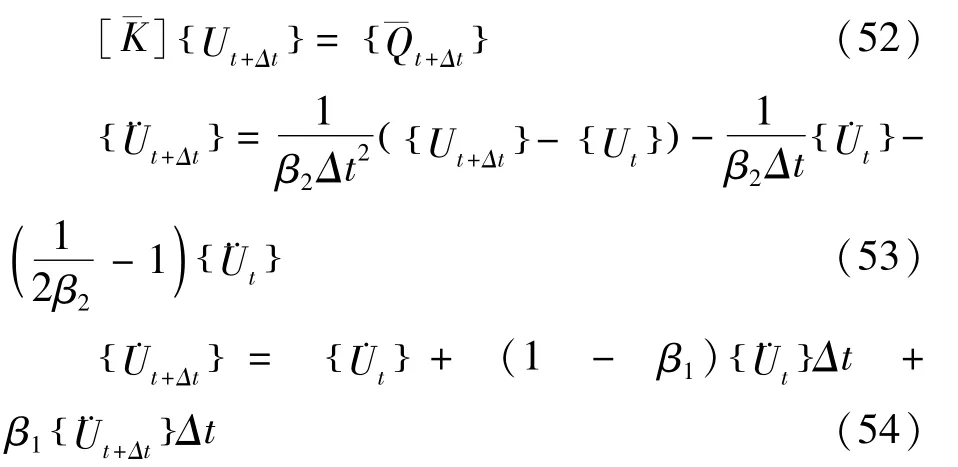
4 数值分析步骤及实例验证
通过分析轴承的载荷,可得角接触轴承的刚度系数,综合含不平衡质量激励的刚性圆盘的运动微分方程式(6)-(7)、通过集总质量模型建立弹性轴段的运动微分方程式(14)-(15)及考虑载荷对轴承刚度影响的轴承座的运动微分方程式(22),建立质量阵[M]、刚度阵[K]及回转矩阵[G],得到转子系统的运动微分方程式(33)。
经状态变量替换,转子系统的临界转速及模态振型问题,转化为求解式(42)特征值及特征向量问题,通过MATLAB程序中Eig函数可以得到转子系统的临界转速,将特征值代入方程求解其特征向量可得对应阶次的模态振型。通过Newmark法求解非齐次线性微分方程式(42)可得到在刚性圆盘的不平衡激励作用下的不平衡响应。
为验证临界转速计算的正确性,本文计算了《转子动力学》中的两端简支的单盘转子系统实例,如图1所示,由于文献中未考虑转子质量,故将其密度设为ρ=1kg/m3,支撑为忽略阻尼的刚性支撑,刚度为K=7×106N/mm,具体参数如表1所示。

表1 单盘转子系统参数
基于MATLAB编写转子系统的有限元法分析程序,将转子系统等分为76个节点,圆盘位于第26个节点上,给定转子自转角速度Ω,通过求解式(41)的特征值,得到对应于该转速的正进动频率ωF1、ωF2及反进动频率ωB1、ωB2,如表2所示。
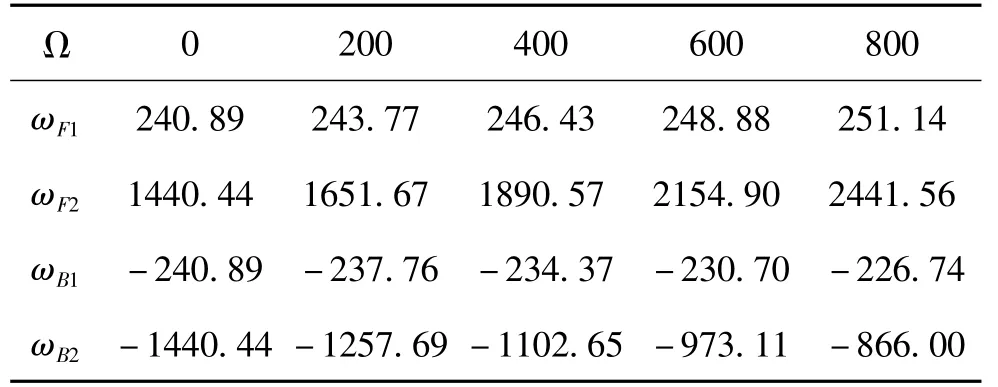
表2 单盘转子系统进动频率 (rad/s)
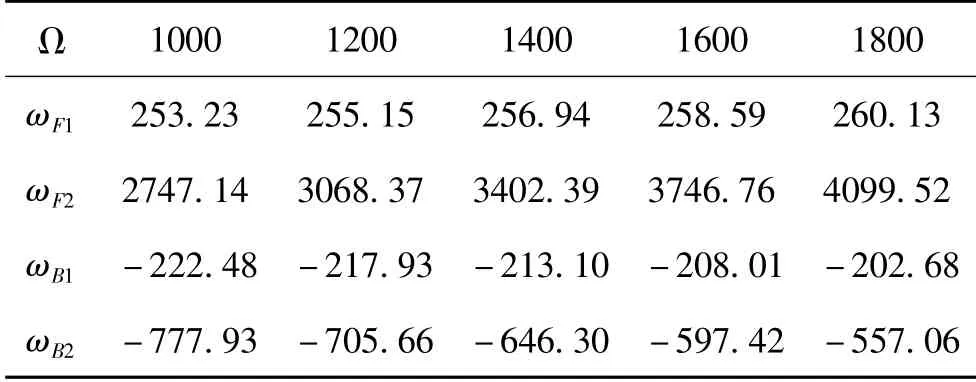
表2 (续) 单盘转子系统进动频率(rad/s)
以转子自转角速度Ω作横坐标,对应的正、反进动角速度为纵坐标,即将表2作图,如图5所示。
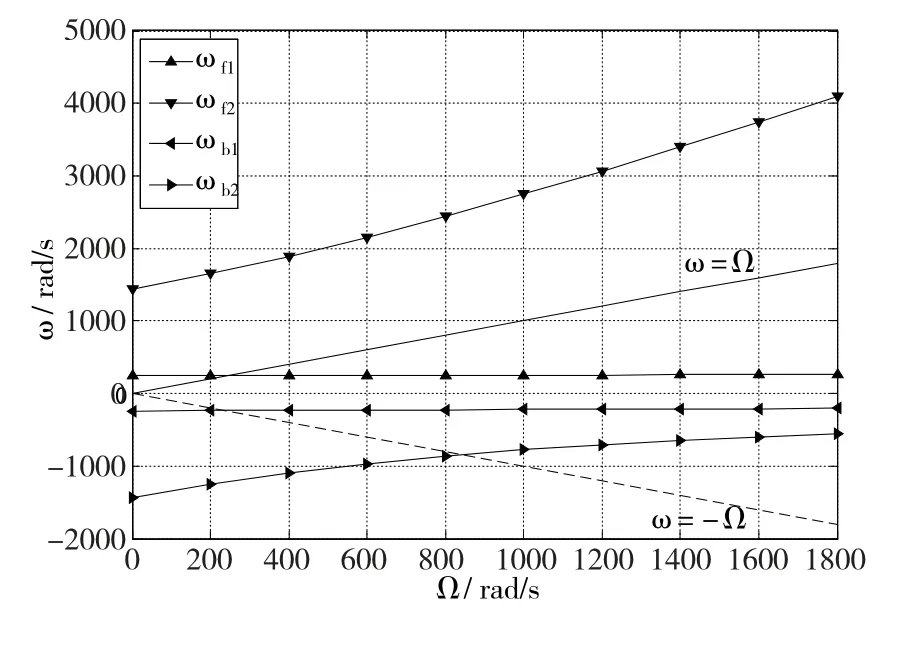
图5 单盘转子系统正反进动频率
作直线Ω=±ω与曲线ωF1、ωB1及ωB2相交,得到按绝对值大小排序的转子系统的临界转速,其中第二阶为同步正向涡动时的临界转速,如表3所示。从表可以得出,本文临界转速的分析计算与文献中的计算结果误差很小,计算结果很精确,表明程序的分析计算结果可信。
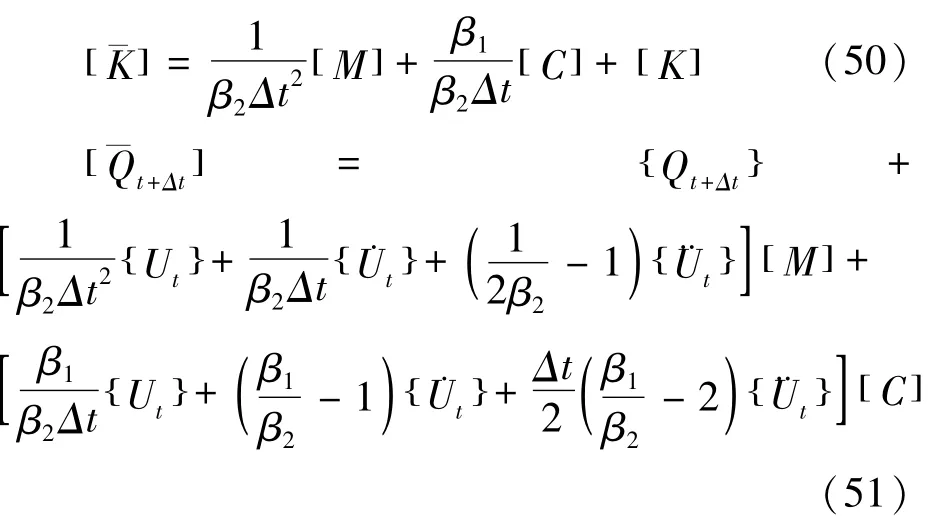
单盘转子系统对应于表3前三阶的临界转速的模态振型通过求解式(41)的确定,如图6所示。图中前三阶的临界转速下的模态振型在形状和趋势上与理论上的振型基本一致。
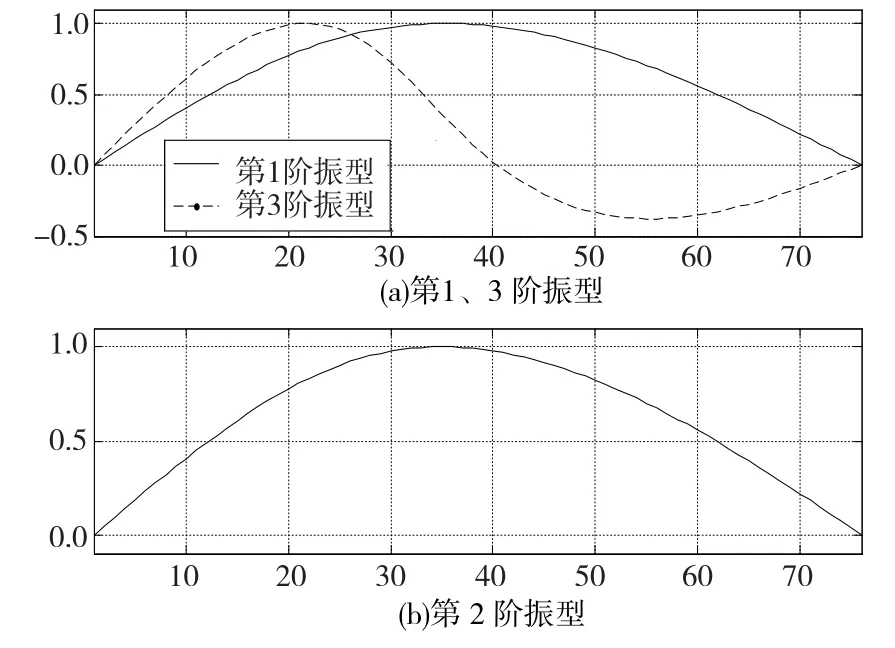
图6 单盘转子系统主振型
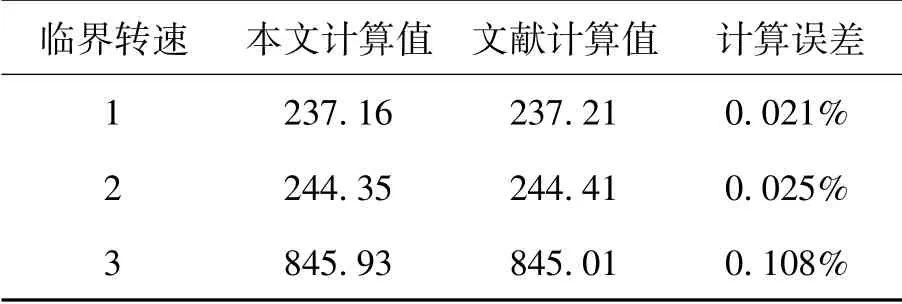
表3 单盘转子系统临界转速 (rad/s)
单盘转子系统刚性圆盘引起的不平衡响应,可由轴承转子系统的运动微分方程式(42)通过Newmark解法确定。通常,实际转子在刚性圆盘不平衡质量的激励下将作同步正向涡动,因此,更加重视同步正向涡动的临界转速,不考虑同步反进动的临界转速,如图7所示,转子在临界转速为ω=244.35rad/s附近幅值出现了峰值。
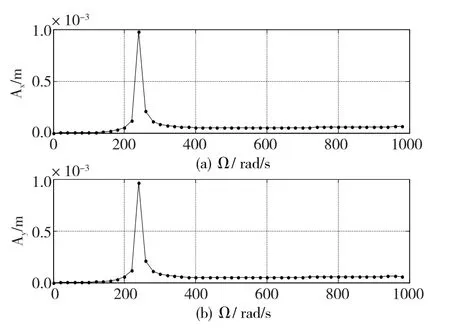
图7 单盘转子系统不平衡响应
5 结论
(1)详细介绍了主轴单元有限元建模分析方法,首先建立轴承转子系统的有限元模型,求解系统的质量矩阵、回转矩阵与刚度矩阵,得到系统的运动微分方程。
(2)使用MATLAB编写转子系统的有限元法分析程序,利用MATLAB程序中的Eig函数求解系统临界转速、Newmark-β方法求解系统运动微分方程不平衡响应。
(3)以两端简支的单盘转子系统为实例验证了MATLAB数值分析的正确性。

