基于高斯过程回归的电网运行方式快速置信评价

刘季昂，刘友波，邱高，王吉利，丁茂生，刘挺坚

（1.四川大学电气工程学院，四川省成都市 610065；2.国家电网公司西北分部，陕西省西安市 710048；3.国网宁夏电力有限公司，宁夏回族自治区银川市 750001）

0 引言

随着新能源渗透率的提升，电网的不确定性显著增加，电网运行方式的组合数也大大增加。典型运行方式已不能涵盖所有新能源随机组合场景，因此，调度部门应综合考量多种因素，及时编制或调整运行方式，以提高电网运行的可靠性、安全性和经济性。

运行方式编制包括典型方式制定、方式评价、方式调整等步骤。其中，典型方式制定一般采用数据或经验驱动方法，根据给定的先验原则将历史方式聚类、分簇，并划分出具有代表性的几类典型场景，属于统计学问题［1-2］。方式调整则以典型方式为基础，根据日前运行需求进一步调整，调整过程中以多维方式评价指标为指导，实现电网在给定边界条件下的趋优运行。传统方式调整主要依靠专家反复调整可控量，在保证潮流收敛和安全校核通过的前提下，兼顾评价指标的优化。但是，随着电网评价指标多样性的提升，调度人员在面对大量互相关、互制衡指标时难以快速择优，且部分指标的计算也降低了方式评价和调整的效率，增加了隐形人力和计算成本。因此，亟需准确、高效的运行方式评价方法，以辅助提升运行方式的可观性及其调整效率。

运行方式评价一般包含2 个方面:一是全面合理的指标体系构建，该体系构建应基于系统性、科学性、可比性原则，并能完整、准确、客观地反映电网运行水平；二是采用科学客观的指标融合方法提升运行方式评价的可观性。例如，文献［3-4］分别建立了智能电网评估指标体系和地区电网运行方式评价体系，但缺失电网安全评估的关键指标。由于评价指标涵盖广且互相关，不利于调度人员把握方式优劣，而多维指标融合标定是工程实用的评价方案，因此，可以提供可行的解决方案。目前主流的指标融合方法包括层次分析法［5］、模糊决策理论［6］、熵权法［7］等。如文献［8］引入多算子模糊层次分析法实现年尺度下的高维指标融合，并验证了该方法的有效性。文献［9］提出了基于贝叶斯网络的改进熵权-模糊层次分析法，将主观权重的获取转化为最大分布概率区间的采样问题，减小了少数专家偏好的主观影响。但上述方法受制于指标计算效率。

本文旨在提出运行方式的综合、快速评价方法，为调度人员提供高效且直观的方式调整反馈。因此，本文首先选取了安全性、稳定性和经济性3 个维度下的多类关键指标，借助电压-无功直流潮流、智能暂态稳定评估等进行计算，并通过熵权-模糊层次分 析（entropy weight-fuzzy analytical hierarchy process，EW-FAHP）法对多维指标进行融合标定。最后，引入了具备置信解析度的高斯过程回归（Gaussian process regression，GPR），快速构建指标与电网关键变量间的数值关系，建立运行方式快速评价的模型。该模型能够计算后验置信区间，并为调度人员提供不同置信度的指标评价值，保证了评价的可靠性。所提方法能够对运行方式进行综合评估，为调度人员提供运行方式调整的即时反馈，从而提升调度互动友好度，改善方式编制效率，节省人力和计算成本。

1 运行方式评估体系及指标

本文重点考虑安全性、稳定性、经济性3 个维度，选取了线路、电压、新能源消纳、暂态稳定性等方面的指标，构建了一套运行方式评价指标体系，如图1 所示。其中，指标的选取参考了文献［3-4］及实际需求。值得指出的是，本文所提评价方法具备较强通用性，可兼容更多宏观或微观指标。为简化描述并更直观展示所提方法框架，本文仅选取具有代表性的几组指标。

图1 电网运行方式评价指标Fig.1 Evaluation indices for operation modes of power grid

1.1 安全性指标

1）N-1 通过率

在C（N-1）次N-1 校核试验中，切除系统中任一元件（如发电机、线路等）后未出现过负荷，且频率、电压均未越限的次数占比定义为N-1 通过率:

式中:I(N-1)为N-1通过率；C(N-1)，pass为校验通过次数。

2）线路负载率指标

通过线路负载率的平均值μl和标准差σl来反映全网线路负载率平均水平以及各线路间的不均匀程度，采用等值概率评估算法［4］进行量化计算，如式（2）所示:

式中:ILR为线路负载率指标；r为自变量。

1.2 稳定性指标

1）电压合格率

电压合格率主要体现运行点的电压合格水平，并可全局性地反映节点的运行电压质量。

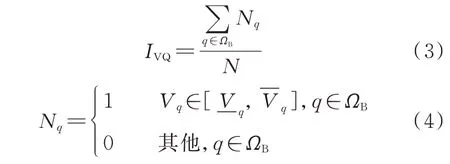
式中:N为总节点数；分别为节点q的电压、电压下限、电压上限；ΩB为节点集合；Nq为表示节点q是否合格的变量；IVQ为电压合格率。

电压合格范围设置为发电厂和500 kV 变电站的220 kV 母线电压0～+10%的变化范围，220 kV 变电站110 kV 和35 kV 母线电压-3%～+7%［10］的变化范围。

2）电压偏移率

与线路负载率指标相似，使用等值概率评估算法［4］对各节点电压的偏移情况进行量化，如式（5）所示:

式中:μv和σv分别为节点电压偏移率的平均值与方差；IVB为电压偏移率；v为自变量。

3）静态电压稳定指标

为评估系统的静态电压稳定性，本文选取负荷裕度指标表示［11-12］，并通过连续潮流模型求解计算。计及负荷增长参数λ的潮流方程如式（6）所示:

式中:Pg，i和Qg，i分别为节点i的发电机有功和无功出力；PL，i和QL，i分别为节点i的负荷有功功率和无功功率；Gij和Bij分别为节点导纳矩阵元素的实部和虚部；θij为节点i与j之间的相角差；Vi和Vj分别为节点i和节点j的电压幅值；λg、λL、λQL分别为发电机出力、负荷有功功率、负荷无功功率的增长系数；j∈i表示与节点i相连接的节点集合。

递增λ并结合参数化策略［13］确定系统电压的临界失稳点。求取负荷裕度λcr，则静态电压稳定指标ISVS为:

4）暂态功角稳定指标

暂态稳定性主要体现当前运行方式下受大扰动后维持稳定的能力，一般采用暂态稳定评估（transient stability assessment，TSA）方法求取。本文考虑如式（8）所示的暂态功角稳定（transient angle stability，TAS）指标:

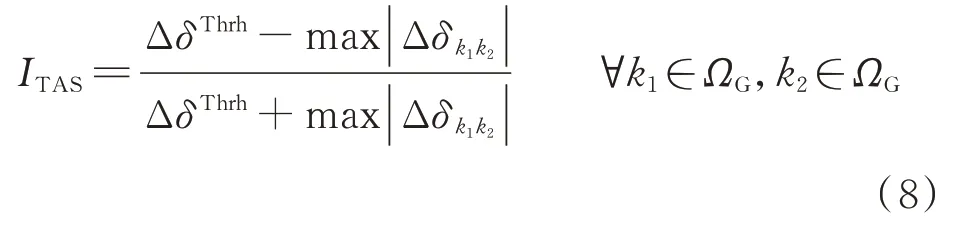
式中:ΔδThrh为提前定义的功角差阈值；为第k1台和k2台发电机之间的功角差；ΩG为常规发电机集合；ITAS为TAS 指标。

为了真正模拟暂态过程，需对动态元件（如同步发电机）进行精确的状态和参数估计。但在多预想事故集下，大规模状态估计在效率与精度方面都具有挑战性。因此，基于人工智能的TSA 模型得到了大力发展，通过将暂态稳定评估封装在参数化模型中以替代状态估计。大量研究已表明，决策树［14］、深度学习［15］等机器学习技术在应用于实际TSA 时具备极高的精度以及较强的可行性。本文使用智能TSA 模型对TAS 指标进行计算，相关模型见附录A。

5）暂态电压稳定指标

系统暂态电压稳定性可通过微分-差分-代数方程（differential-difference-algebraic equation，DDAE）进行求解。本文采用时域仿真法，结合实用判据［16］，设置暂态电压稳定指标为:

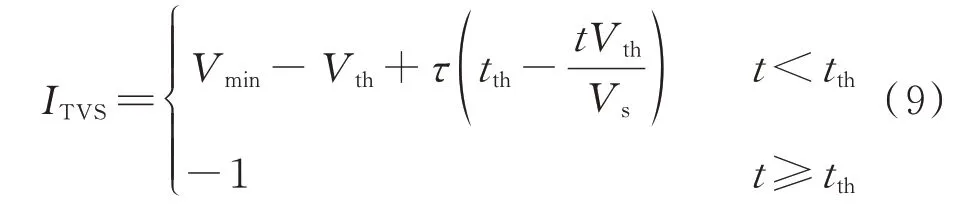
式中:Vth为电压暂态稳定阈值，Vth=0.75 p.u.；tth为允许电压低于阈值的持续时间，tth=1 s；τ为临界电压偏移时间因子；Vmin为故障后节点电压最小值；t为节点电压低于阈值时间；Vs为故障后的稳态电压。

1.3 经济性指标

1）新能源消纳能力指标

电网消纳新能源能力主要取决于发电机调峰能力、新能源接入下的系统运行安全性等因素。根据目前主流研究，新能源消纳能力计算方法可分为两大类:1）第1 类是基于简单的线性组合假设［17］，亦或者结合线性模型与新能源随机分布［18］的方法，该方法可以快速估算新能源消纳能力，虽然计算效率高，但是难以反映网络约束，可能导致一定评估误差；2）第2 类是建立以新能源消纳为目标的随机优化模型［19］的方法，该方法能够更准确地描述系统数学模型，因而也能更精确地评估新能源消纳能力，但存在收敛速度慢的问题。本文后续将利用数据驱动方法快速评估消纳能力，由于该方法对离线计算效率要求不高，但依赖于精准的样本标签集，因此，本文采用第2 类方法评估新能源消纳能力。

综上，本文主要以发电机出力、新能源切机量为决策变量，建立以新能源消纳最大为目标的随机优化模型，并考虑了潮流等式约束、运行约束和备用约束。考虑到交流潮流在新能源消纳随机分析中极难收敛，本文采用改进直流潮流约束［20］，如式（10）所示:

式中:P为有功功率向量；B为节点电纳矩阵；θ′为不计入平衡节点的相角向量；θN和θM分别为PQ和PV节点相角向量；UN为PQ节点电压幅值向量；H、F、h为由电网拓扑决定的常数矩阵或向量，其计算详见附录B。

同时，考虑到实际运行中不同新能源厂站的可能最大出力并非独立分布，为构造合理的随机新能源场景生成模型，需要考虑新能源出力间的相关性。本文基于Copula 函数生成新能源随机场景［21］，最终通过蒙特卡洛模拟实现新能源消纳评估，具体模型详见附录C。

最终通过式（4）计算新能源消纳能力指标IREC为:

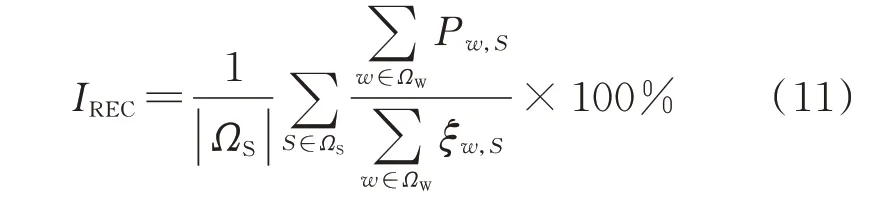
式中:ΩS为新能源出力随机场景集合；ΩW为新能源发电机集合；Pw，S为场景S下新能源发电机w的出力；ξw，S为场景S下新能源发电机w实际可达出力，为随机变量；|ΩS|表示ΩS中的元素数量。

2）网损率

将电网的总网损Ploss与负荷总水平的比值定义为网损率IPL，如式（12）所示:

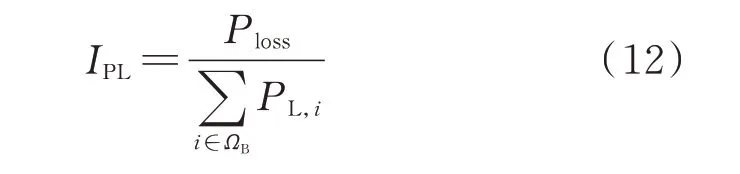
3）发电成本

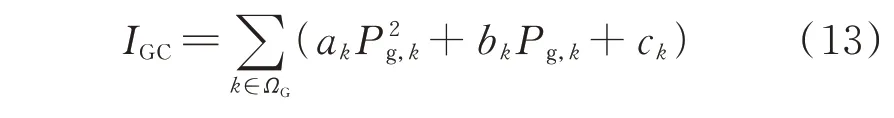
式中:ak、bk、ck为发电机k的运行成本系数。

2 电网运行方式的层次分析评价模型

2.1 归一化处理

由于电网运行方式评价体系中各指标的取值区间存在差异，为保证评价的严格性，需对其进行归一化。本文采用理想点逼近法将各项指标值变换至［0，100］区间内，如式（14）所示:

式中:I为某项特定指标；I＋和I－分别为该指标的正、负理想解（通常为不可行解）；Inorm为指标的变换值。

2.2 熵权-模糊层次分析法

为解决主观赋权法易受专家主观偏好影响和客观赋权法过于依赖原始数据的问题，本文选取EWFAHP 法对多维运行方式评价指标进行融合。权重计算模型被分为主观、客观2 个独立计算模型，具体实施步骤如下，详细内容可参考文献［22-23］。

1）建立模糊判断矩阵Z=(zsh)n×n，其中

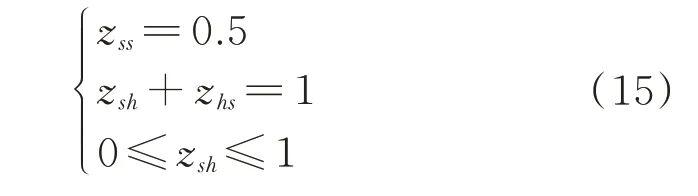
式中:zsh为指标s相对于指标h的重要程度，s=1，2，…，n，zsh=0.5 表示2 个指标同样重要，且zsh取值越大代表指标s相较于指标h越重要；n为指标数量。

2）计算主观权重并检验一致性。结合文献［22］，采用式（16）计算主观权重Ψs:

3）计算客观权重，如式（17）所示:

式中:s=1，2，…，n；psl为样本l的第s项指标归一化后的数据；Rsl为样本l的第s项指标数据；es为第s项指标熵值；ωs为样本l的第s项指标权重；m为数据样本数。

4）计算综合权重Ws，如式（18）所示:

在指标层与子指标层内建立模糊矩阵并计算主观权重，同时检验一致性；逐层计算主观权重，直至求出顶层的主观权重后再计算客观权重和综合权重，最终获得运行方式的综合评价指标。

3 运行方式快速评价方法

在制定运行方式过程中，通过前述方法对运行点进行评价的效率往往不能满足调度实际要求，不利于方式部门快速制定运行计划。此外，2.2 节的EW-FAHP 法虽然综合了主观先验和客观数据分析的优势，但依赖于历史样本数据分析，使得评价方法在计算熵权时会产生额外的计算负担。为了解决上述问题，使得方式编制人员能够更快速地根据方式变化判断运行状态优劣，从而提升方式编制的灵活性和效率，本文提出基于数据驱动的电网运行方式快速评价方法。所提方法能够直接挖掘历史数据模式，给出运行点与综合指标间的直接数值关系，进而能够快速评价运行方式并快速修正运行计划。

此外，考虑到数据驱动模型的本征误差，可能导致模型评价运行方式过于乐观，使得运行计划保守性不足。为解决此问题，本文引入GPR。GPR 是一种随机机器学习方法［24］，能够给出预测点的置信区间信息，因而可对运行方式进行保守评价，有利于辅助提升系统运行的鲁棒性。

3.1 基于原理

首先定义表征电网运行方式的特征集合x:

式中:ΩD为负荷节点集合；M为特征维度；Pg和Pw分别为常规发电机、新能源发电机的有功功率向量；Qg和Qw分别为常规发电机、新能源发电机的无功功率向量；Pd为负荷功率向量；Vb为节点电压向量。

为快速评价运行方式的优劣，将第2 章所得综合评价指标作为GPR 目标特征y∈R。至此，构建了运行方式快速评价模型的数据集结构，由（x，y）表示。

在年运行负荷数据先验分布以及各设备额定运行范围内进行随机抽样，共抽取β组样本，即可生成运行样本集X=［x1，x2，…，xβ］∈Rβ×M，每一组样本特征对应一个目标值，则有Y=［y1，y2，…，yβ］∈Rβ。整合构成带标签的样本集（X，Y），以此训练GPR模型。

考虑如式（20）所示的线性回归模型:

式中:ζ为回归系数；ε为预测误差，在GPR 中一般给定先验为独立正态分布，ε～N（0，σ2），其中σ为方差，考虑其独立性，该项相当于高斯过程中的协方差矩阵对角线增加σ2。

引入基函数ϕ(x)，将x投影到高维特征空间中，以提升线性模型表征能力，并引入高斯过程使得线性模型残差可控，得到GPR 模型:

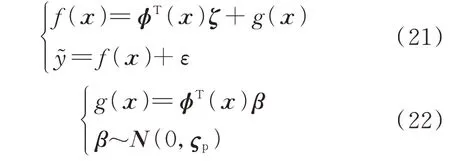
式中:g（x）为贝叶斯线性回归函数；β为满足均值为0、协方差为ςp的先验正态分布；f(x)为中间函数。

g（x）的高斯过程可由式（23）表示:

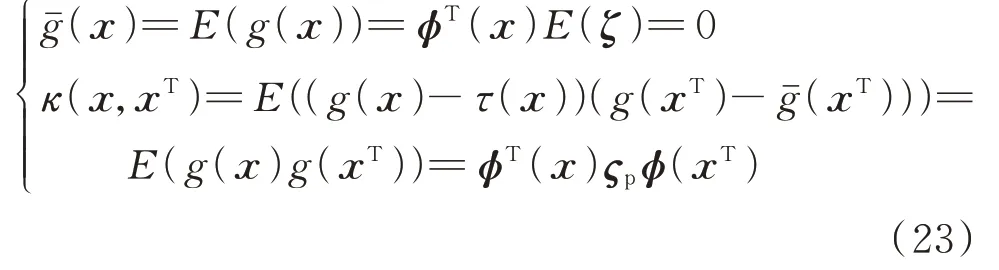
式中:E（·）为表示期望的函数；(x)为期望值；κ（x，xT）为g（x）的协方差函数（covariance function，CF）。

注意到ςp由先验分布给出且正定，因此κ(x，xT)可由核函数进行参数化，核函数则需要根据实际问题进行试验择优选取。本文经试验选取性能最优的平方指数核函数，如式（24）所示:

式中:η=[of，ol]，为GPR 超参数，其中，of为信号标准差，ol为特征长度。

考虑ε的独立假设，并基于已知样本数据集可生成g（x）的分布如式（25）所示:

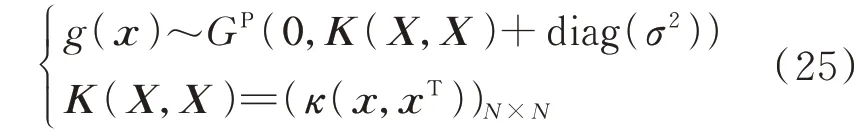
式中:GP为高斯过程函数；diag（σ2）为由σ2构成的对角线化矩阵，为了便于描述，记为σ2I，I为单位矩阵；K（X，X）为κ（x，xT）扩展至矩阵的表达式。

结合式（21）和式（24），可得线性模型f（x）的后验分布为:

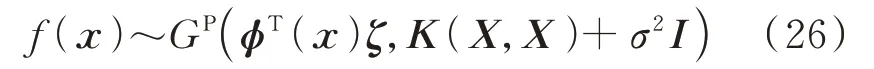
在此基础上，结合式（20），可求取综合评价指标的最大似然估计，如式（27）所示:

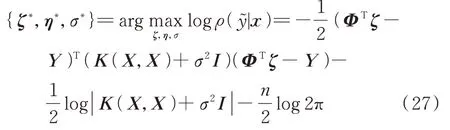
式中:ζ*、η*、σ*为待求取参数；Φ为由训练集数据计算的ϕ(x)构成的矩阵。

3.2 运行方式保守评价

基于传统数据驱动方法建立的运行方式评价模型存在精度不足、估计过于乐观的问题。方式人员对评价模型的保守性把握不足，可能导致最终编制的运行方式存在风险。基于式（21）所得GPR 模型，可以得到运行方式评价的均值以及标准差，从而可提供明确的评价置信信息，提升方式制定的保守性，降低实际运行风险。具体计算公式如式（28）所示:

注意到，式（28）中各等式右边最后一项与当前运行方式无关，为常数。式（28）给出了运行方式评价综合指标的条件分布估计值，即:

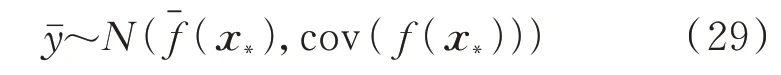
在此基础上，可以对电网运行方式进行置信评价，以95%置信区间为例，某一运行方式x*下的综合评价结果为:

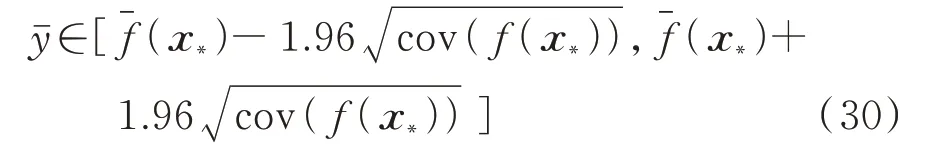
在实际应用中，方式部门可根据需求选取评价指标区间的上下界，以制定激进或保守的运行方式。

4 算例分析

本文采用改进IEEE 39 节点系统进行测试。在节点17 处集中接入装机容量为350 MW 的风场，风机型号为HOMER 提供的AOC 15/50［25］，其功率曲线见附录B 图B1；在节点21 处集中接入装机容量为380 MW 的光伏电站。新能源渗透率为系统总装机容量的10%。在新能源消纳能力评估模型中，上、下旋转备用率为10%，最终基于蒙特卡洛模拟法和Cplex 进行计算［26］。在稳定性指标方面，节点电压的合格范围设为额定电压的-10%～10%，暂态失稳阈值ΔδThrh为180°。

4.1 新能源不确定性建模

本文时序风速和光伏数据基于HOMER 软件生成，其中光照数据来源于经纬度为（106°30‘，36°0’）的地区，详见附录C 图C2（a）。

利用Copula 建立计及相关性的风光联合出力模型，详细过程见附录C。

4.2 权重计算

1）主观权重:按照调度经验对指标进行评估，根据4 种不同的关注重点（A、B、C、D）打分并两两比较后获得模糊判断矩阵Z1、Z2、Z3、Z4，分别检验一致性并计算权重，结果如表1 所示。

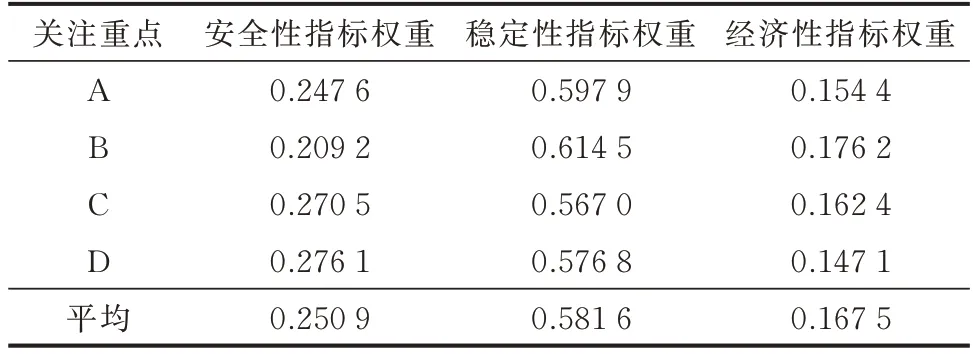
表1 主观权重计算结果Table 1 Calculation results of subjective weights

2）客观权重:根据电网运行方式数据计算安全性指标、稳定性指标、经济性指标的客观权重，分别为0.441 4、0.319 5、0.239 1。

3）综合权重:根据式（18）对主、客观权重进行耦合，可得到安全性指标、稳定性指标、经济性指标的综合权重分别为0.329 1、0.551 6、0.119 3。

由表1 可以看出，根据专家给出的模糊数生成的主观权重会受到部分专家偏好的影响，使得权重值有偏差；而通过熵权法计算客观权重并进行耦合，能够在一定程度上修正这一偏差，从而使最终的权重能较为充分地反映出专家的集中意见。

4.3 运行方式评估分数与分析

采用本文所提指标体系与方法获得各项指标值及其综合权重后，进一步计算算例电网运行方式的综合评价分数。选取120%负荷水平工况下的3 种不同运行方式来模拟方式编制时的大负荷场景，并分别计算其评价分数，结果如表2 所示。由表2 数据可知，3 种运行方式中方式3 综合评分最高，方式2 综合评分最低，且评分差值主要体现在安全性指标中，其余2 类指标较为接近。在各运行方式中，稳定性指标分值占比最大，经济性指标分值占比最小，与综合权重分布相对应。

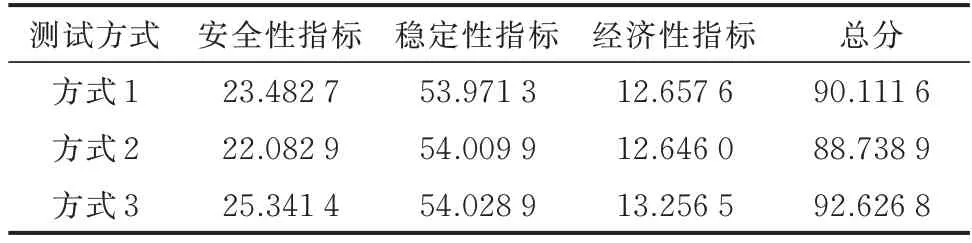
表2 运行方式指标计算结果Table 2 Calculation results of operation mode indices

此外，为了更好地研究子指标层中各指标在3 种运行方式中的情况，将方式1、2、3 在子指标层中的各项指标的评分采用理想点逼近技术进行处理，使不同权重、不同分值的子指标能够统一在区间［0，1］内进行比较，其结果如图2 所示。

图2 不同运行方式下各项指标评分比较Fig.2 Comparison of each index score in different operation modes

显然，3 种运行方式在IREC、ISVS与IGC这3 项指标上的差异较大，在ILR、ITAS与ITVS这3 项指标上有轻微差异，其余几项指标较为接近。这表明3 种运行方式在新能源消纳能力与发电成本2 个方面具有明显差异。在新能源消纳和静态电压稳定方面，方式1 表现最为出色，方式2 次之，而方式3 最差；在发电成本方面，方式3 成本最低，方式2 次之，方式1 成本最高。另外，与表2 中数据结合来看，由于评价体系中新能源消纳能力与静态电压稳定指标的权重均明显高于发电成本的权重，使得方式3 在发电成本高的情况下依旧能获得最高评分。

另外，考虑到运行方式编制为实际的工程问题，本节选取中国西北某省电网在2018 年4 月大、小负荷水平下风光不同出力时共计8 种典型运行方式进行测试。测试结果如表3 所示。

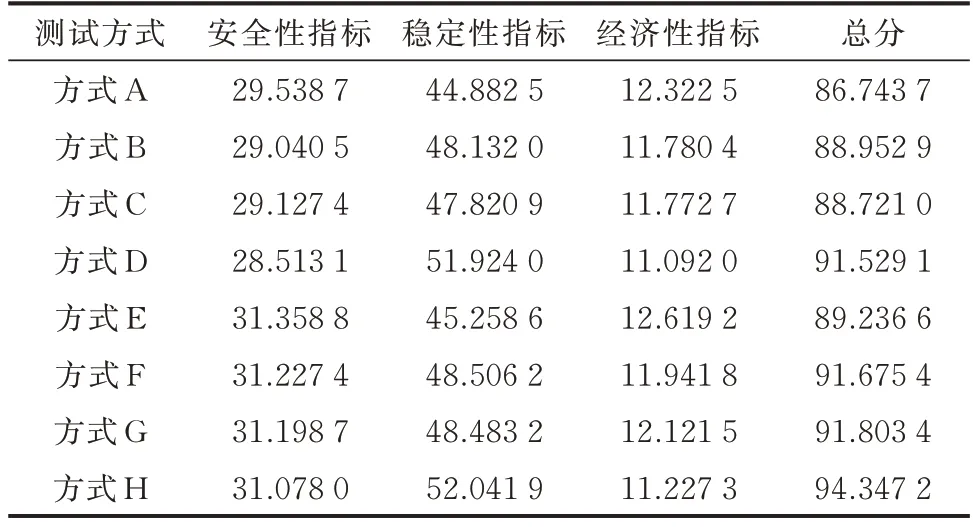
表3 实际电网测试结果Table 3 Testing results of actual power grid

由表3 可知，当风光出力占比相同时，大负荷水平的评分略低于小负荷水平。当负荷水平一定时，风0%和光0%出力的方式总分最高，风70%和光80%出力的方式总分最低。结合各项指标进行分析，可以看出，风70%和光80%出力时方式A、E 的稳定性指标较低，而安全性和经济性指标较高。这是因为高比例风光出力提高了运行方式的新能源消纳指标，但同时对电网的稳定性造成影响。此外，因该省新能源装机容量的占比较高，风光出力减小时，需增大火电出力弥补缺口。此时，该省电网的省间断面由外送电变为受电断面，整体的线路负载率相对上升。因此，运行方式的安全性指标有所下降。而由于评价体系中稳定性指标的权重相对高于经济性指标的权重，方式D、H 获得同负荷水平下的最高评分。从上述分析中可以看出，所提评价体系能够较为系统、全面地对某地区的电网运行方式进行评价。

同时，为进一步验证所提方法在非典型运行方式下的有效性，以实际电网小负荷水平下风70%和光80%出力的典型方式为基准，设置发电机有功出力在95%～105%范围内波动，随机生成100 个运行方式，并分别计算各随机运行方式的评分，结果如表4所示。

由表4 结果可知，随机运行方式样本中存在个别样本潮流不收敛，而其他潮流收敛的随机方式评分与典型方式相比明显较低。这一结果能够说明从一系列随机运行方式中筛选出高评分方式可作为典型方式筛选的依据之一，且在方式调整过程中该评分有助于方式计算人员快速选择并确定调整方向。

表4 随机生成运行方式的测试结果Table 4 Testing results of randomly generated operation modes

4.4 运行方式快速评价模型验证

本节采用绝对相对误差（absolute relative error，ARE）、平均绝对百分比误差（mean absolute percentage error，MAPE）以及最大绝对误差（maximum absolute error，MAE）作为运行方式快速评价模型（以下简称本文模型为GPR 评价模型）的性能量化指标。APE 及MAPE 由式（31）计算:

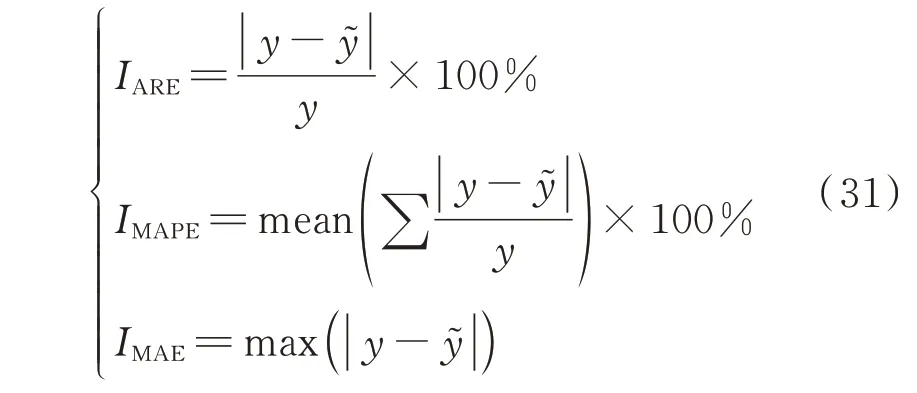
式中:mean（·）为均值计算函数；IARE、IMAPE、IMAE分别为ARE 指标、MAPE 指标和MAE 指标；max（·）为求取最大值函数。

在改进的IEEE 39 节点算例中，抽取1 000 个运行方式数据，通过第2 章方法对各运行方式样本进行评分，生成标签特征。在1 000 个样本数据中900 个划分为训练集，剩余100 个作为测试集对GPR 模型进行测试。测试结果如图3 和图4 所示。

图3 直观表明GPR 模型具备较高的评估精度，在100 个测试场景中表现出了较优的泛化能力，其中最高ARE 不超过0.02%。

图4 表明GPR 模型具备输出置信信息的能力。现有点估计机器学习（如深度学习、线性回归等）虽然能够实现实时计算，但缺乏对其本征计算误差的感知能力。而GPR 模型能够输出一定置信范围内的运行方式评价区间，提高了数据驱动方法的可靠性。若基于GPR 模型的运行方式评价的指标区间较宽，则说明GPR 模型对当前运行方式的评价不确定性较高，此时方式部门可采取较为保守的评价值，如区间下界、下分位点等。此外，由图3 和图4 可以看出，GPR 模型的指标估计结果基本和真实指标值保持一致趋势，说明GPR 模型能有效提取到运行方式关键变量与指标的关联关系。同样的，采用实际电网数据对GPR 模型进行测试，可以得到相近的测试效果，在100 个测试场景中最高ARE 不超过3%。

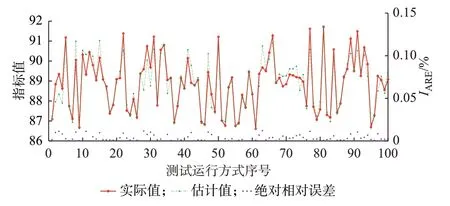
图3 实际指标与估计指标值对比Fig.3 Comparison between actual indices and estimated indices

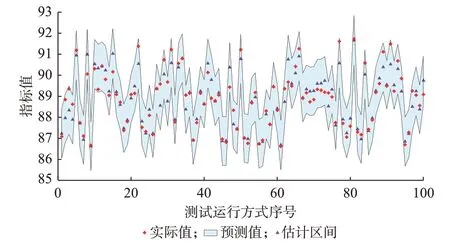
图4 基于GPR 模型的运行方式评价结果Fig.4 GPR-based assessment results of operation modes

为进一步验证所提GPR 模型的优势，本文将所提模型与常见机器/统计学习算法进行对比试验，参与试验的算法包括反向传播神经网络（backpropagation neural network，BPNN）、深度置信网络（deep belief network，DBN）、回归树（regression tree，RT）、支持向量回归（support vector regression，SVR）以及弹性网络回归（elastic net regression，ENR），结果如表5 所示。

表5 基于各类学习算法的运行方式快速评价模型测试结果Table 5 Testing results of fast assessment model for operation modes based on various learning algorithms

由表5 可知，基于DBN 的快速评价模型表现出最优性能，其次为GPR 模型。但是，DBN 模型无法提供评价的置信度，而GPR 模型可以输出置信度信息，为方式部门提供更可靠的评估结果。其他算法精度均不及DBN 和GPR。通过以上分析可知，GPR 模型更适用于可靠的运行方式评价，而具备更高评价精度的DBN 模型可用做初步的点估计参考。总之，所提方法评价精度较高。

如表6 所示，在计算效率方面，模型驱动方法中部分指标计算比较耗时，导致模型驱动的方式评价效率偏低。以新能源消纳能力评估为例，其评估过程中需要对蒙特卡洛抽样生成的100 个随机场景进行优化计算，因此，耗时较长。而所提方法无须进行耗时的指标计算，仅须采用简单的高斯过程进行计算，因此，计算时间低于1 s。在实际电网中，考虑到电网规模增大所带来的数据量与数据维度的增加，上述计算效率的提升效果也将更加明显。所提方法能够为方式部门调整运行方式提供快速、准确的反馈结果，进而可有效提升运行方式调整的效率，节约人力成本和计算成本。

表6 计算效率统计结果Table 6 Statistical results of calculation efficiency

5 结语

本文提出了基于GPR 的电网运行方式多维指标的快速置信评价方法。针对评价指标计算难的问题，利用电压-无功直流潮流、智能暂态稳定评估等简化指标计算，使评价体系得以有效计及复杂稳定问题；针对运行方式评价指标种类多、相关性不明确问题，通过一种可权衡主客观的EW-FAHP 法，实现多维指标融合标定；针对复杂指标计算导致的方式调整反馈低效问题，引入具备一定置信解析度的GPR，实现运行方式的快速、综合、置信评价。所提方法能够高效支撑方式编制人员进行“试凑”或经验式的运行方式制定，提升编制效率、降低人力成本。算例结果表明，所提运行方式评价方法具备较高精度，计算效率达到秒级。此外，其能够输出方式评价的置信信息，保证了运行方式评价的可靠性，为调度部门提供了有力的决策支撑。

需要说明的是，本文是在典型方式已提前制定好的假设基础上，针对方式调整过程中方式评价分析效率不足问题，开展了相关研究，旨在为调度部门提供方式调整过程中更迅速的评价反馈。因此，本文并未考虑新型电网发展下的典型方式制定问题。充分利用历史运行经验或数据，将所提运行方式评价方法与数据驱动方法相协调，以指标引导典型方式制定，弥补现有典型方式制定方法缺乏数据和经验有机融合的缺点，将是未来的主要研究方向。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。