考虑信息时移的分布式光伏机理-数据混合驱动短期功率预测

王彪，吕洋，陈中，赵奇，张梓麒，田江

（1.东南大学电气工程学院，江苏省南京市 210096；2.国网苏州供电公司，江苏省苏州市215004）

0 引言

分布式光伏的有效利用是推动中国能源生产和消费革命的重要手段。然而，由于其功率的随机性和波动性，分布式光伏并网后对配电网安全、电能质量以及系统稳定性等产生的影响不容忽视［1-2］。因此，分布式光伏功率的准确预测，对多层级电网的运行优化有着重要意义。

目前，集中式光伏预测的研究相对成熟。从建模逻辑出发，可以分为两大类。一类是机理驱动方法，由气象信息和光伏系统参数，依据物理原理建立预测模型［3-4］。另一类是数据驱动方法，通过分析历史出力、气象信息等数据间的关系，建立预测模型。常用的方法有统计方法［5］、机器学习方法［6-7］和融合方法［8］等。

分布式光伏预测可以借鉴集中式光伏预测方法。但相较于集中式光伏站点，分布式光伏数量众多，地理分布分散，逐一为各站点配置功率预测的计算成本太高。基于多用户出力的空间相关性进行聚类，进而预测整个光伏集群的功率是一种经济有效的解决方法［9-11］。然而，分布式站点出于成本考虑往往没有购买数值天气预报（NWP）服务，缺乏预测所需的同时空气象数据信息。影响光伏出力的天气、辐照度等因素在同一地区较为接近，因此，基于空间相关性，借助邻近信息完备的集中式光伏站点的数据推算区域内分布式光伏的功率是一种可行的方案。文献［12］基于Copula 函数构建了各类天气下分布式光伏和集中式光伏的出力相关性模型。文献［13］基于逆距离加权算法得到了目标站点的期望输出。然而，在分布式站点与集中式站点存在一定地理位置偏差时，由于太阳的方位不同，其气象条件也会存在一定的时移。直接利用所提供的气象数据或者出力数据进行预测，精度难以得到保证。

此外，物理模型基于机理建模，具有因果逻辑性强、对数据质量不敏感等优点。但分布式光伏由于运维水平、组件工艺等因素，一般难以获得硬件设施的具体参数，基于机理驱动的物理建模只能采用简化模型和经验参数，预测精度相对较低［14］。基于数据驱动的深度神经网络模型，其深层的非线性神经网络可从大量高维样本中学习到深层次特征，实现复杂函数的逼近，预测精度高，但是模型参数完全依赖数据，对数据的质量要求较高，其泛化性能一直备受关注［15-16］。

针对上述问题，本文利用邻近公共气象站点或者配置NWP 的光伏站点提供的气象数据，建立机理-数据混合驱动模型。对于机理驱动模型，根据目标站点的历史功率曲线和NWP 中的辐照度数据，确定气象数据相对于分布式站点的最优时移，对气象数据进行调整，解决物理模型的气象数据偏移问题。对于数据驱动模型，引入时间模式注意力（temporal pattern attention，TPA）机制［17］，利用一维卷积提取多种时间模式，通过注意力机制实现对气象数据时间偏移的纠正。此外，通过特征工程对输入进行特征优化，提高单个学习器的性能。在此基础上，通过Stacking 集成学习融合机理驱动模型和数据驱动模型的优点，进一步提升模型的泛化性能和预测精度。

1 数据预处理

1.1 考虑地理位置偏移的气象信息时移

在一定范围内，不同位置点的光伏出力存在着空间相关性，为根据附近其他地理位置点（集中式光伏站点或公共气象站点）提供的NWP 进行分布式光伏预测提供了基础。由于不同地点的太阳辐照度等气象条件存在一定的时间偏移［4］，需要利用这种地理位置造成的时移特性对气象数据进行校正，从而提高预测精度。理论上，通过分布式站点和提供NWP 数据站点的经纬度信息，可直接确定时间偏移量。但考虑到光伏站点运维不完善导致的经纬度信息无法获知等因素，本文通过平移集中式站点的历史气象曲线，使之与分布式站点的出力曲线相关性最高，从而确定相应的时移量。因此，首先通过皮尔逊相关系数（PCC）对NWP 中的主要气象因素与光伏出力之间的相关性进行表征，选择与出力相关性最高的气象因素作为计算最优时移的参照量。附录A 图A1 所示左侧子图为一天的光伏出力与不同气象因素的时间序列图，右侧子图为8 d 的光伏出力和气象因素的关系图，图中，r表示相应的PCC 值。从图中数据可以看出，总辐照度与光伏出力相关性最高，故选择总辐照度作为确定最优时移的参照量。

以原时间点为初始位置，对总辐照度历史数据进行左右平移，分别计算平移后的总辐照度和每个分布式站点历史功率的PCC，选择使PCC 达到最大的平移量作为该站点的气象数据最优时移量。短期功率预测数据的时间间隔ΔT=15 min，意味着最优时移量的精度为15 min。考虑到存在站点地理位置偏移带来时移量为非整倍ΔT，为了提高最优时移的精度，采用三次样条插值对总辐照度数据进行加密，生成时间间隔Δt=5 min 的高密度数据。如图1所示，最优时移的计算步骤如下:

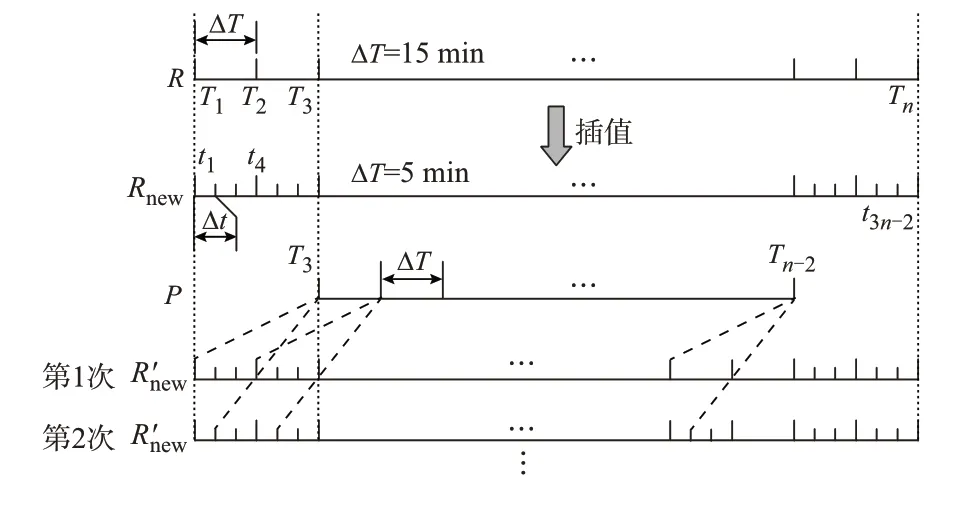
图1 最优时移计算示意图Fig.1 Schematic diagram of optimal time-shift calculation

通过上述方法对气象数据进行修正，为提高机理驱动模型预测精度提供了数据基础。

1.2 特征工程

特征工程是把原始数据转变为模型训练数据的过程。目的是获得更好的训练数据特征，以便于模型学习到本质规律。本节利用领域知识和一些数学分析方法对模型的输入数据进行预处理，将原数据转换为合适的特征数据，为数据驱动模型做数据准备。

将NWP 提供的所有变量作为深度学习的模型输入，以尽可能考虑所有影响因素，包括气温、直射辐照度、风速、风向和时间信息等。

首先，对风速Ws和风向Wd进行处理。风向Wd用角度表示，但角度并不是一个好的模型输入，如0°和360°应该相互靠近、平滑衔接，然而其在作为深度学习模型的输入时，差异反而是最大的。并且，当Ws=0 时，Wd对功率应没有影响。风速和风向实际上是极坐标下的极径和极角的含义，因此，对Ws和Wd进行坐标变换，转换为直角坐标系下的分量Wx和Wy:

风信息特征构建前后对比见附录A 图A2。从图中可以看出，处理后的风信息特征更为平滑、集中，作为深度学习的输入具有优势。然后，对时间信息进行处理，包括年、月、日、时、分、秒等，气象条件的变化以及光伏出力的变化具有强周期性特征，这种时间周期性可以给预测模型提供重要的特征信息。与风向相似，年、月、日、时、分、秒六要素的原始时间向量并不是一个合适的模型输入。在处理后，23:59:59 数据应该与次日的00:00:00 数据平滑衔接，当年12 月数据应与来年1 月数据相近。通过傅里叶分解得出气象数据存在一天和一年两个明显的周期，分析见附录A 图A3。利用三角函数构建以年和天计的周期信号特征如下:

式中:Dsin和Dcos为以天计的周期特征；Ysin和Ycos为以年计的周期特征；tdur表示从某个时间点到当前时间点的持续时间。

最后，对所有NWP 进行特征缩放，以消除每个变量的量纲、数值量级不同对模型的影响。本文采用区间缩放法对输入特征进行无量纲化，将所有特征数值统一到[-1，1]区间:

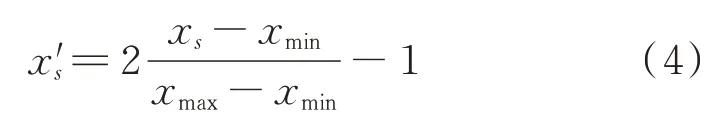
式中:xs为特征x的第s个样本值；xmax和xmin分别为特征x的最大值和最小值；x′s为归一化数值。如附录A 图A4 所示，处理后的特征数值总体分布更加集中。

2 预测模型

2.1 光伏预测机理驱动模型

光伏发电功率物理模型通过光伏站点的地理位置和NWP 数据计算出光伏面板接收到的总辐照度，再通过辐照度到功率的映射模型得到光伏面板的功率输出，计算流程见附录A 图A5。

分布式光伏投资小，一般采用固定角度安装，光伏发电出力的效率PPV的表达式为:

式中:η为光伏系统的光电转换效率；APV为光伏阵列的面积；It为光伏板接收到的总辐照度。

光电转换效率η主要由两部分组成，其参数方程为［18］:

式中:Tc为光伏面板运行温度，计及风速和热量散失的光伏模块温度模型见文献［4］；a1、a2、a3为参数。

将光伏面板面积系数和光伏系统效率方程中的待定参数进行归并，形成新的整合后的功率映射方程:

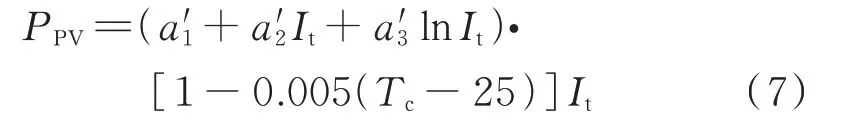
由功率映射方程可知，当面板辐照度It和面板运行温度已知的条件下，可采用最小二乘法对参数进行估计，具体步骤见附录B。

2.2 基于TPA 机制的数据驱动模型

长短期记忆（long short-term memory，LSTM）网络是一种经典的循环神经网络模型，通过精妙的门设计，一定程度上解决了梯度消失的问题，从而能够计及长期信息的影响，适合处理具有长期依赖的时序预测问题。

细胞状态是具有记忆功能的单元，是LSTM 网络的关键。细胞状态如同传送带，信息随着时间在整条链上流通，实现信息留存，形成“记忆”。ht为t时刻的隐藏状态，同时也是t时刻的单元输出。LSTM 网络的各门控逻辑和输出的计算公式见文献［17］。

注意力机制聚焦视场中关键信息，忽略次要信息，从而更高效地获取全局特征的上下文信息，提高模型性能。本文采用TPA 机制挖掘当前光伏功率点和相邻气象信息时间位点的关系，从而纠正数据驱动模型的气象时移。TPA 机制的原理见附录C图C1。卷积神经网络（CNN）具有强大模式捕捉能力，因此采用多个一维卷积核对时间窗口中的隐藏层矩阵进行卷积，生成多个时间模式:

式中:Hi为LSTM 网络隐藏层矩阵第i个行向量；Cj为第j个卷积核；表示相应的卷积值。

注意力机制类似一种查询操作，将该步隐藏层状态作为查询项，时间模式矩阵HC相当于字典，通过评分函数计算字典中每个条目的相关性分数f(，ht):

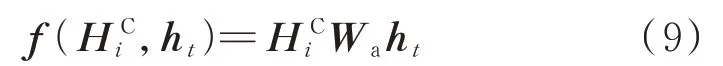
式中:为时间模式矩阵的第i个行向量；Wa为注意力机制的系数矩阵。

得分通过激活函数得到相应注意力权重αi。由注意力权重αi计算时间模式矩阵行向量的加权和，得到上下文向量vt:

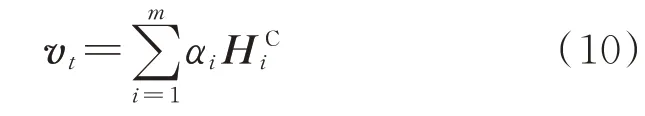
式中:m为时间模式矩阵HC的行数。

将上下文向量和隐藏层状态进行整合，通过一个全连接层得到该时间步的输出:

式中:Wh为全连接层权重；［·］表示两个向量的拼接操作。

最终的封装模块见附录C 图C2，将LSTM 网络的输出和注意力机制生成的上下文信息向量进行拼接，经全连接层映射为一维标量，再经过RELU 激活函数得到最终的预测输出值。

2.3 Stacking 集成学习方法

集成学习是一种机器学习范式，多个学习器被训练用于解决同一个问题。集成方法试图构建一组假设并将它们组合起来，以缓解单一模型预测准确率呈现边际效应递减的趋势，提高模型精度和泛化性能。Stacking 集成学习框架首先将原始数据集划分为若干子数据集，输入第1 层预测模型的不同基学习器中，每个学习器输出各自预测结果。再将第1 层基学习器的输出作为第2 层预测模型元学习器的输入，得到最终预测结果。

不同算法模型本质上是在不同的数据空间角度和数据结构角度来观测数据，再依据自身的观测情况及自身算法原理建立相应模型。选择差异度大的算法模型能最大程度发挥不同算法的优势，取长补短，获得更好的组合效果。

Stacking 集成学习的具体训练方式见文献［19］。元学习器的训练样本是基学习器的预测输出，如果直接使用基学习器的训练集预测输出作为第2 层模型的训练集，可能会产生严重的过拟合。因此，本文采用了k折交叉验证的Stacking 方法，从而避免了数据的重复学习。在模型应用阶段［20］，将经过预处理后的NWP 数据输入给对应的基学习器，每种方法对应实例化模型各有k个，将k个预测结果取平均后输入元学习器得到最终的预测结果。

2.4 基于Stacking 集成学习的机理-数据混合驱动模型

本文采用5 折交叉验证的Stacking 集成学习框架，为获得更好的组合效果，第1 层基学习器选择机理驱动的物理模型和数据驱动的TPA 机制模型。元学习器的输入训练样本特征变量只有两个。这主要考虑到很多变量本质上都是对同一气象数据的预测，不同基学习器的预测输出存在多重共线性问题，因此元学习器选择带有非负约束的最小二乘 法（non-negativity constraints least-squares，NCLS）［21］解决了稀疏特征的欠拟合问题，同时提高了元学习器的泛化能力，防止过拟合。

本文预测模型的训练流程如图2 所示，首先，对NWP 数据进行预处理，对于物理模型（图中用PHY表示）而言，将所需气象数据进行最优时移处理；对于TPA 机制模型而言，依次进行特征提取和特征缩放。然后，将处理后的数据集划分成5 等份，训练基学习器，每种模型都会得到5 个参数不同的实例模型。将基学习器的预测结果作为元学习器输入，再训练元学习器。模型应用流程见附录D。

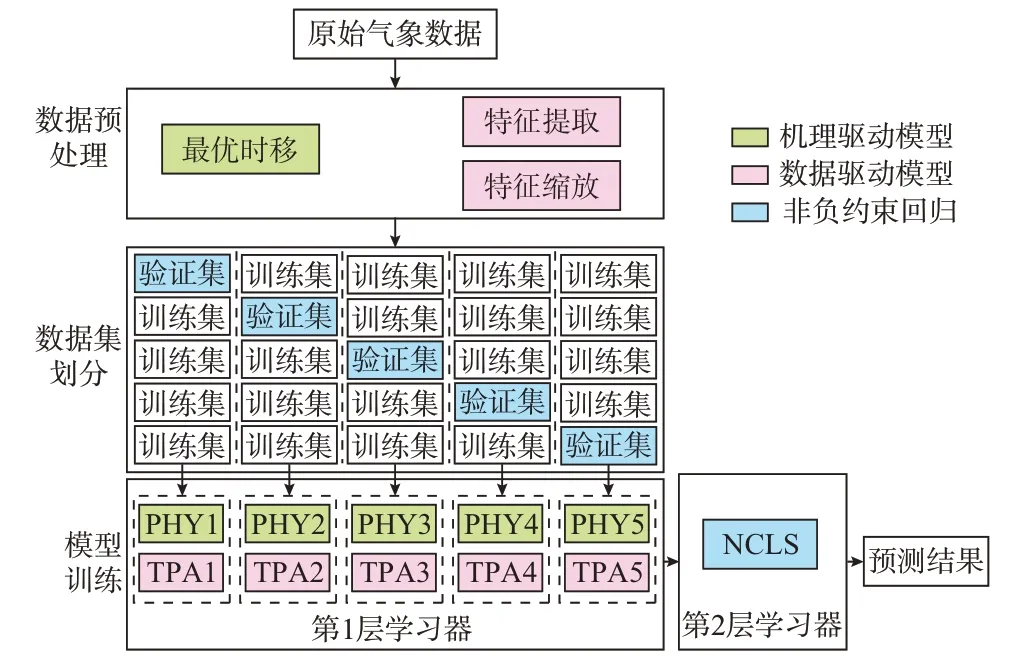
图2 机理-数据混合驱动模型的训练流程图Fig.2 Flow chart of training for hybrid mechanismdata-driven model

3 算例分析

光伏出力数据来源于国际太阳能研究中心（International Solar Energy Research Center，ISC）所提供的德国康斯坦茨分布式光伏数据［22］，NWP 数据来源于Solcast 机构［23］，相关数据说明和模型参数见附录E。本文采用不同指标从多方位对模型性能进行评定，包括平均绝对误差（MAE）、归一化平均绝对误差（NMAE）、均方根误差（RMSE）、归一化均方根误差（NRMSE）和拟合优度（用R2表示），相关公式见附录E。

3.1 最优时移分析

时移前8 个不同地点的光伏功率曲线和气象站点处的总辐照度曲线见附录E 图E1。从图中可以看出，8 个站点的分布式光伏由于安装容量和光伏板类型等不同，功率曲线的峰值和形状有所差异，但是曲线整体走势基本一致，且与气象站点处的总辐照度曲线相似，这说明了将公共气象站点数据用于多点分布式光伏预测的可行性。随机选取2 d 的天气数据，首先对时间间隔为15 min 的原始气象数据采用三次样条插值的方法进行数据加密，生成时间间隔为5 min 的密集化数据，见附录E 图E2。插值后的点形成的曲线光滑，能够充分拟合出曲线的走势。

由密集化后的总辐照度数据通过左右平移的方式依次计算与光伏功率的PCC 值，每次平移一个点位（5 min），左右最大平移量为10 个点位（45 min），选择最大PCC 值对应的时移量为最优时移。搜索过程和各站点最优时移量见附录E 图E3 和图E4。

为了验证时移能够有效提升物理模型预测精度，以站点1 的2016 年4 月11 日数据为例，对两种场景下的物理模型预测结果进行对比，如图3 所示。从图中可以看出，考虑了时移之后，预测曲线整体向右侧移动，与实际功率曲线贴合更紧密。

图3 时移对物理模型的影响Fig.3 Effect of time shift on physical model

为了更充分地说明时移对预测的影响，对经过最优时移处理的数据集分别采用数据驱动和机理驱动的方式进行训练，预测8 个分布式光伏站点出力，见附录E 图E5。对于TPA 机制模型而言，最优时移处理提升了3 个站点预测精度，降低了4 个站点的预测精度，一个站点最优时移为0，时移为0 的情况无须讨论。可见，对于TPA 机制模型，最优时移处理并没有产生稳定的影响结果。这是由于数据驱动模型中TPA 机制能够自动提取对应于当前时间步输出影响大的输入时间点，学习到最优时移量，无须输入数据的时移预处理。对于模型驱动模型的影响分析见附录E。

3.2 特征工程的影响

选取站点1 说明特征工程对数据驱动模型预测结果的影响。2 d 的预测结果时序图见附录E 图E7，在2016 年6 月3 日12:00左右（图中的红色虚线框），没有进行归一化的无处理和特征构建两种情形下，都出现了一段功率不变的平直区。而采用了归一化方法的两种情形的功率曲线变化更加顺滑和细腻，能够及时跟踪气象变化。这是因为在没有进行归一化的情形下，一些重要特征的微小变化湮没在数值较大的特征中，使得微小变动的影响被掩盖，预测曲线出现平直区。进一步对比8 个站点在有无特征工程处理下的预测结果，如图4 所示。以NRMSE 指标对预测精度评价，从图中可以看出，特征构建和归一化处理对模型预测精度的提升都有显著的效果。特征构建产生结构更好的特征，让模型的学习变得容易。归一化能够消除特征本身巨大的数值差异，从而使得数据驱动模型更容易学到各个特征本身对功率输出的影响，体现特征的属性性质。两种处理方式的同时使用，更进一步提高了预测精度。

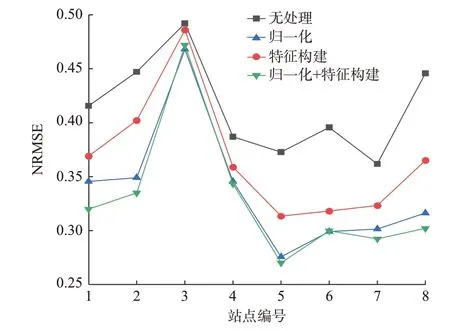
图4 特征工程对各站点预测的影响Fig.4 Effect of feature engineering on forecasting of each station

3.3 元学习器的对比

本文采用非负约束的最小平方优化作为元学习器，求解基学习器的最优组合，缓解多重共线性问题。为了验证非负约束的最小平方优化的有效性，本节选取了简单平均法（simple averaging，SA）、普通最小二乘法（ordinary least square，OLS）、多层感知机（multilayer perceptron，MLP）和LSTM 网络作为元学习器进行对比，预测结果的误差见附录E图E8。SA 通过简单地对物理模型和数据驱动模型取平均得到预测结果，OLS 通过对每个时间点两种模型预测结果的组合权重进行优化，进一步提升了预测精度。

对比OLS 优化和带有非负约束的最小平方优化，可以看到后者在训练集上的RMSE 较大，在测试集上较小，由于对权重进行了非负约束，有效防止过拟合，从而在测试集上有更好的表现。作为神经网络模型的代表，LSTM 网络相对于MLP，其精度有所提高，但是较统计学方法所得的结果精度相差甚远。对比基准模型SA，从训练集上可以看出，MLP 和LSTM 网络训练集上的RMSE 为平均模型的几十倍，都存在欠拟合的问题。由于MLP 和LSTM 网络中的参数个数较多，对于特征变量较少、特征之间高度相似的输入而言，反向梯度传播难以训练出性能好的模型。因此，元学习器不宜选择复杂度较高的神经网络类模型。

3.4 不同预测方法性能比较

为了验证本文所提方法的有效性，将本文所提方法与其他经典方法做对比，包括所提方法第1 层基学习器的物理模型、数据驱动模型以及其他经典模型。其他经典模型选择了机器学习中的支持向量机（support vector machine，SVM），树模型中的极端梯度提升（extreme gradient boosting，XGBoost）和深度学习中的LSTM 网络。模型超参的选择对模型的性能会产生很大的影响，为了使得实验对比更加具有说服力，本文采用贝叶斯优化的方法对单一模型的超参进行寻优。各单一模型的参数配置见附录E 表E4。

选取一个典型日，对8 个站点不同预测方法的曲线进行展示，见附录E 图E9。基于5 个评估指标，对不同方法下8 个分布式站点的预测结果进行对比，如图5 所示。其中，拟合优度为越大越优，其余4 个指标为越小越优。从图中可以看出，SVM 方法在站点6 的各项指标都较好，站点1、3、7 和8 的各项指标相较其他方法最差；XGBoost 方法在站点3 的RMSE、NRMSE 和R2指标上最优，在其他站点上的各项评价指标较差，整体上优于SVM 方法；深度学习网络LSTM 整体比传统机器学习方法SVM 和XGBoost 预测性能优越，稳定性较好；物理模型稳定性较差，在站点4、5 和6，各项指标相较于其他方法均最差，在站点1、3、7 优于机 器学 习方法SVM 和XGBoost；TPA 机制方法作为时下较为先进的预测模型，精度高、泛化能力强，在各个站点的指标都优于经典的深度学习方法LSTM 网络；融合模型在各个站点的各项指标都要优于单一的物理模型和TPA 机制模型，这说明了集成学习框架通过对基学习器的优化，能够有效提升方法的预测性能，除了站点3 的部分指标低于XGBoost 方法，在其他所有站点的各项指标上均为最优。综合各项指标，本文所提物理-数据混合驱动方法的预测精度和泛化性能最优。该方法能够对NWP 数据进行修正，有效提高分布式光伏短期功率预测的精度。

图5 8 个站点预测指标雷达图Fig.5 Radar diagrams of forecasting indices of eight stations

4 结语

本文针对分布式光伏站点功率预测气象数据缺乏的现状，结合机理驱动、数据驱动方法的优势，提出了一种考虑信息时移特性的分布式光伏机理-数据混合驱动功率预测方法。通过实际数据进行验证，结论如下:

1）对于机理驱动模型，通过分析主要气象信息与光伏出力的相关性，确定了总辐照度作为最优时移的特征量。通过最优时移搜索校正气象数据，从而有效提高了机理驱动模型的预测精度；通过三次样条插值对气象数据进行密集化，提高了时移的精度。

2）数据驱动模型中，通过引入TPA 机制，使得模型在预测中能够自主选择对应时间步的输入，从而解决气象信息时移问题。

3）通过Stacking 集成学习框架融合两种基学习器，综合不同算法的优势，获得了更优预测结果。

在今后的工作中，有必要综合天气类型、地理信息和电网拓扑等因素，对数量众多、分布广泛的分布式光伏进行动态分区，进一步提升各分区功率预测的准确性，降低计算负担。另外，可进一步研究插值间隔对最优时移的影响。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。