考虑捎带能力变化的两阶段高铁物流装运方案

王雅宁，马啸来

（1.西南交通大学，交通运输与物流学院，成都 611756；2.综合交通大数据应用技术国家工程实验室，成都 611756）

0 引言

随着高铁网络建设的加快，截至2020年底，我国“八纵八横”高铁网已初步成型[1]。为充分利用高铁网运能，中铁快运通过确认车运输、捎带运输及货运专列运输等组织模式开展高铁物流业务。与其他两者相比，捎带运输具有可利用列车数多、到发时间灵活等优势，是最主要的运输组织模式[2]。该模式下，制定装运方案，为列车分配待运货物是物流业务得以开展的基础。但从方案制定至列车开始装运作业的时段内，旅客仍可购票、退票、改签以及变更到站，列车上座率并非固定不变，捎带能力亦会随之动态变化，初始装运方案的准确性难以保证。因此，有必要针对考虑列车捎带能力动态变化的高铁物流装运方案开展研究。

既有研究中，国内方面，朱晔等[3]研究了在列车运输能力和车站作业能力不足的情况下，列车运输能力在各车站之间和各类需求之间的平衡分配问题。刘勇等[4]以车站办理货运作业次数最小为目标，对基于既有列车运行图的高铁行包运输方案进行优化。姚玉莹等[5]在此基础上，考虑了车站装卸作业速率并以列车运行成本与时间惩罚费用之和最小为目标对高铁快捷货物的装运方案进行了研究。王鹏翔[6]考虑了列车运载能力约束和径路运输能力约束，建立了以运输利润最大为目标的运量分配模型。国外方面，尚未有捎带模式下高铁物流装运方案的研究，但存在与之相关的列车货运装配方案研究。Cohn 等[7]针对将行包运输的复杂规划问题分解为多个子问题后导致的无法得到最优解或可行解的情况，说明对装载方案、运输路径和车辆分配进行一体化研究的必要性，并建立了相应一体化优化模型。Zhu等[8]构建了三层时空网络，综合了服务选择和调整、编组策略以及货物路径优化问题。Ahmadreza等[9]研究了美国铁路线路上运行高速客运和货运列车的混合运行战略层次规划，以客货运输成本最小作为列车调整服务的目标，提出可以应用于其他具有不同参数值情形的方法，得出对延迟的容忍度加大可以减少货运需求损失和运输方面总成本的结论。

既有研究均在列车捎带能力固定不变的前提下开展，未考虑装运方案执行过程中列车捎带能力的动态变化情况。基于此，本文以货运费用最小为目标，利用“初始规划+动态调整”的两阶段策略求解考虑列车捎带能力动态变化的装运方案问题。以不干扰旅客运输为前提，在初始规划阶段，构建考虑列车捎带能力、列车停站方案以及货物运输时限要求等约束的装运模型，制定初始静态装运方案[3-6]。动态调整阶段，将该阶段划分为若干个静态子阶段，构建装运方案调整模型，实时调整方案。最后，以某日西成高铁上行方向的货运需求验证策略的有效性。

1 问题描述

考虑列车捎带能力动态变化的高铁物流装运方案问题为：某线路上具有数列捎带能力、停站方案各异的列车，沿线车站存在若干不同时效等级的货物，需在不干扰旅客运输的前提下，为各列车分配待运货物，实现货运费用最小的装运目标。但列车捎带能力会随上座率的波动而动态变化，需根据变动情况调整装运方案。方案制定及调整如图1所示。

图1 中，某线路上有3 列列车，沿线车站间存在3 类不同时效等级的货物30 个。初始规划阶段，结合上述装运约束及目标，制定图1（a）所示的初始装运方案。动态调整阶段，距离列车2 到达C站的剩余时间为30 min时，判断出列车2在D站的捎带能力变动导致其在C 站的装运作业无法执行，因此根据此刻的列车捎带能力情况调整装运方案，得到图1（b）所示的最终装运方案。

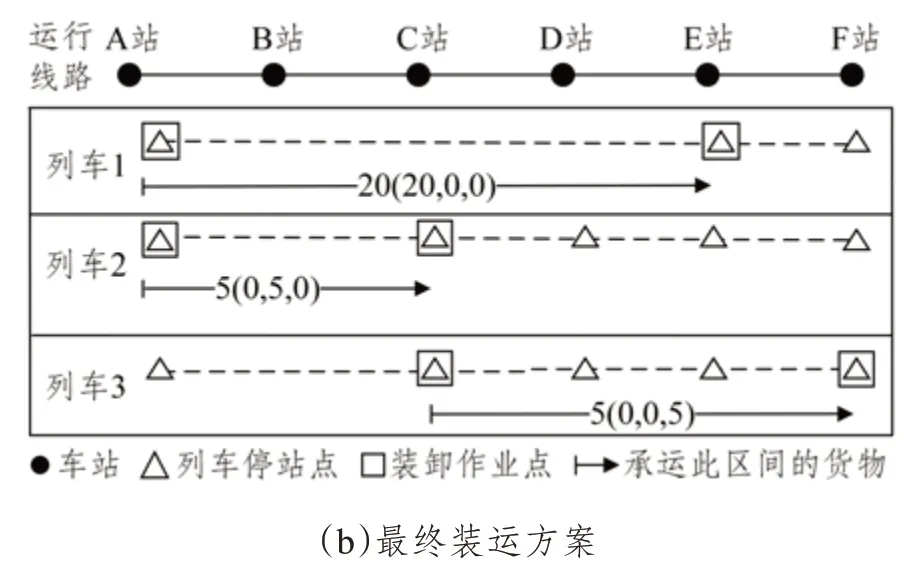
图1 考虑列车捎带能力动态变化的装运方案

2 初始规划阶段

第1 阶段为初始规划阶段。以某时刻为装运方案的制定节点，根据此刻的列车捎带能力制定初始静态装运方案，列车随即按照此方案执行装运作业。

2.1 模型假设

根据问题描述，为便于模型的建立与求解，做出如下假设：

①装运方案制定节点假设

任一装运方案制定节点仅考虑此刻已接收的货物，方案执行期间的新增货物由下一方案制定节点满足。

②列车捎带能力假设

铁路部门在此线路所投放列车的捎带能力可满足此方案制定节点的全部货运需求。

③货物直达运输假设

为降低货运组织工作的复杂性，提高货运效率，制定装运方案时仅考虑货物直达运输。

④货物集装假设

货物已集装至体积、形状、大小均一致的高铁物流箱内且同一物流箱内的货物的目的地及时效等级均相同。

2.2 符号定义

根据问题描述定义以下集合、参数以及决策变量：

①集合

K：待选列车集合，用k表示其中的列车，k∈K；

S：沿线车站集合，用i,j,o,v表示其中的车站，i,j,o,v∈S；

M：待运货物集合，用m表示其中的货物，m∈M。

tm：货物m的待运时刻；

um：货物m应到达目的站的最晚时刻；

qm：货物m单位货物单位时长的时间附加费用，元/小时·箱；

ci：车站i的单次装卸作业费用，元/次；

ei：车站i的装卸作业速率，箱/min；列车k在车站i停车，则=1；否则=0。

③决策变量

2.3 模型建立

（1）目标函数

模型的目标是使货运费用最小。货运费用包括列车运输费用、车站装卸作业费用以及时效性货物的时间附加费用。捎带模式下，列车运输费用可忽略不计，仅考虑后两者。车站装卸作业费用与装卸作业次数及单次装卸作业费用有关。时效性货物的时间附加费用与运输时长及单位货物单位时长的时间附加费用有关：

（2）约束条件

①列车捎带能力约束

任一列车在任一车站经过任何一次装卸作业后，车上的货物总量不超过该列车在此站的捎带能力：

②列车装卸作业量约束

最大允许装卸作业量为列车在此站的停站时长与装卸作业速率的乘积。任一列车在任一车站装卸货物的总量应不大于列车在此站的最大允许装卸作业量：

③列车停站点约束

列车在某车站进行装卸作业的前提是该站点为此列车停站点：

④货物待运时刻约束

货物所搭载列车到达货物出发站的时刻应不早于货物待运时刻：

⑤货物应到达目的站的最晚时刻约束

货物实际到达目的站的时刻不晚于货物应到达目的站的最晚时刻：

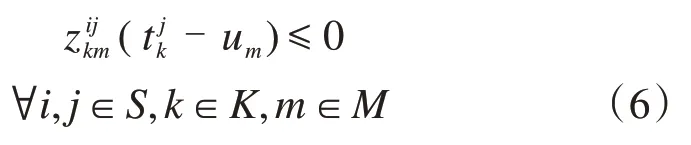
⑥货物运输唯一性约束

每箱货物由且仅由一列列车运输：

⑦货物出发及目的站约束

货物由某列车承运的前提是列车在货物出发站及目的站进行装卸作业：

⑧决策变量约束

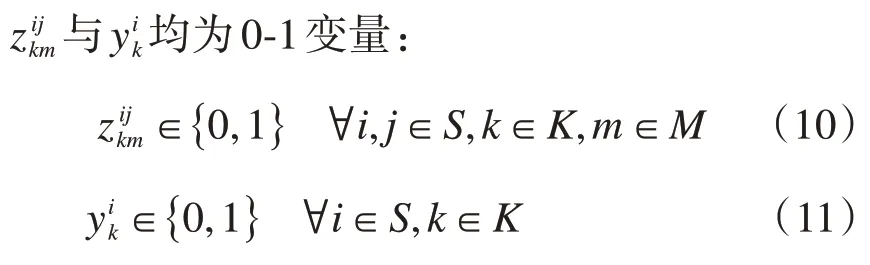
3 动态调整阶段

第2 阶段为动态调整阶段。通过确定方案调整时刻将该阶段划分为若干个静态子阶段。任一静态子阶段结束时刻即为方案调整时刻，根据此刻列车捎带能力情况调整装运方案，随后立即执行调整后的装运方案。

为便于下文描述，将装运作业的最小允许调整时长记作T，仅当某时刻列车到达装运作业站的时间间隔不小于T时，列车在该站的装运作业可调整。

3.1 方案调整时刻的确定

利用图2所示的步骤确定方案调整时刻。

图2 方案调整时刻确定步骤

其中，判断此列车k在i站的装运作业是否可执行的具体方法为：时刻h，是否存在某站使得列车k在此站的剩余捎带能力小于i站所装运货物对此站的捎带能力需求Q箱及以上，若存在，列车k在i站的装运作业无法执行。

3.2 装运方案调整模型

某方案调整时刻，部分列车已完成在部分车站的装运作业或到达部分装运作业站的时间间隔小于T，以上装运作业已不可调整。可调整的装运作业所包含的货物的集合记为Mr(Mr≤M)。

（1）目标函数

模型的目标是使可调整的装运作业中所包含的货物的运输费用最小。货运费用包括车站装卸作业费用以及时效性货物的时间附加费用：

（2）约束条件

①列车剩余捎带能力约束

任一列车在经过任何一次装卸作业后，车上的货物总量不超过列车在此站的剩余捎带能力：

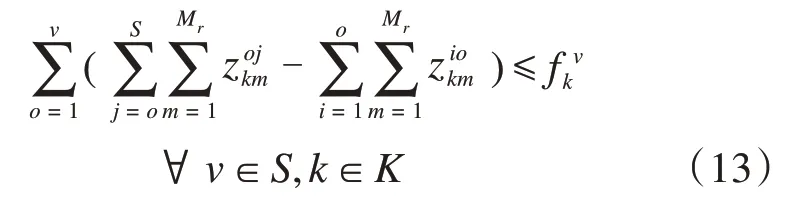
②列车剩余装卸作业量约束

剩余最大允许装卸作业量为列车在此站的剩余停站时长与装卸作业速率之积。任一列车在任一车站装卸货物的总量应不超过列车在此站的剩余最大允许装卸作业量：

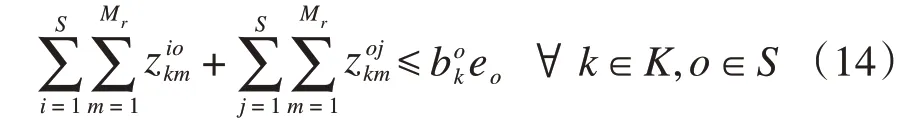
其余约束条件与初始规划模型相同，此处不赘述。

由决策变量可知，初始规划模型与方案调整模型均为0-1 线性规划模型。此类问题可利用LINGO 等求解软件直接求解。因此，本文利用LINGO11.0求解模型。

4 案例分析

4.1 数据准备与处理

以西成高铁为例，选取成都东站、德阳站、绵阳站、广元站、汉中站及西安北站6 座归属于地级行政区的车站作为办理货运作业的待选车站。

4.1.1 货运需求

中铁快运提供四种时效性货运产品：当日达、次晨达、次日达、隔日达。由于列车夜间不开行，因此隔日达产品通常需要一次或数次的中转，故暂时不考虑隔日达产品。其余三种货运产品的时限要求如表1所示[10]。

表1 不同类别货运产品的时限要求

根据各货运产品的截单时刻，选取某日12：00为方案制定节点及货物待运时刻，假定此刻西成高铁上行方向共385 箱货物，如表2 所示。另参考当日达、次晨达、次日达货运产品的收费标准，取其单位货物单位时长的时间附加费用依次为10元/小时·箱、4元/小时·箱、1元/小时·箱[11]。

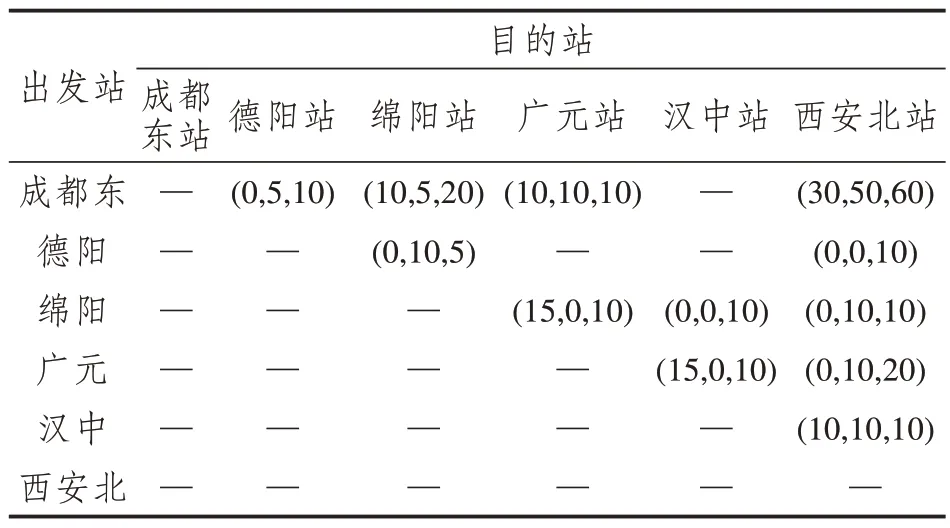
表2 西成高铁上行方向货运需求

4.1.2 列车捎带能力

由于方案制定节点为12：00，因此选取发车时刻晚于12：00 且以西成线上的站点为到发站的17列列车作为待选列车，列车时刻表如表3所示。

表3 列车时刻表

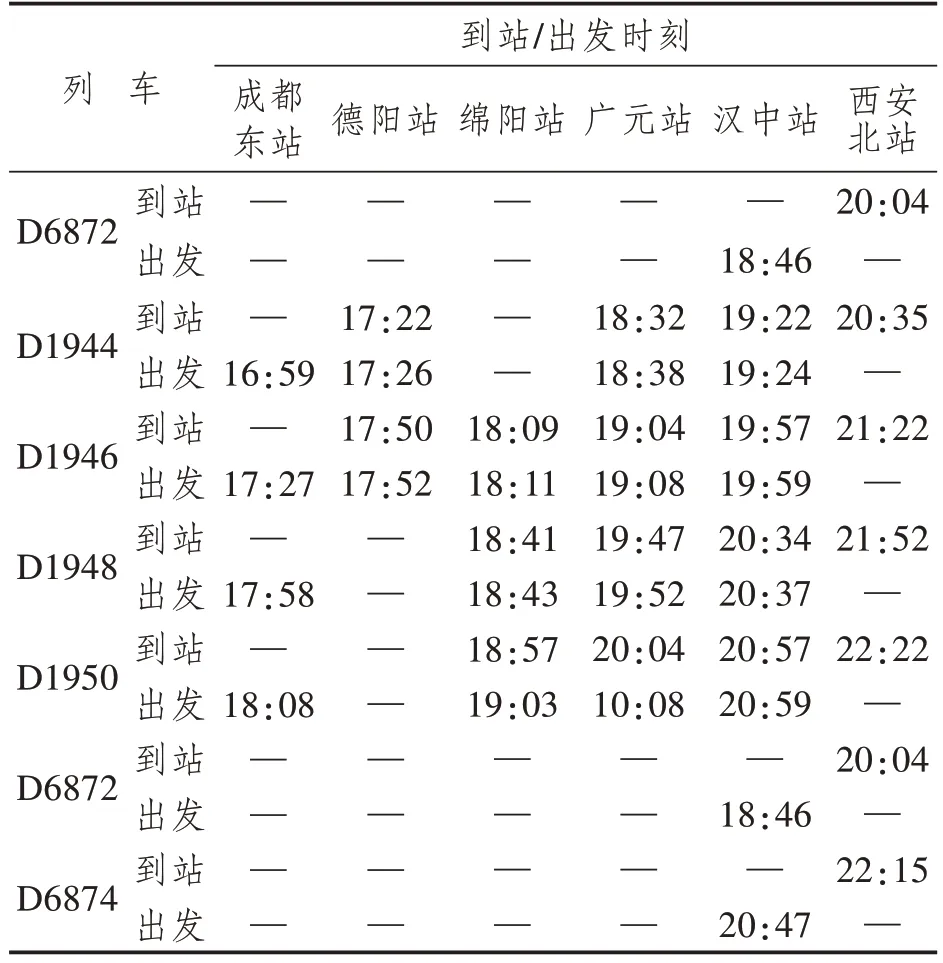
续表3

捎带模式下，列车捎带能力受车型及上座率的影响[12,13]。且货物可被放置在大件行李存放处与最后一排座椅后空档处，但上述位置必须预留不少于三分之一的空间供旅客使用[14，15]。因此，列车在各站点的捎带能力可表述为：

取一节车厢的捎带能力为9 个物流箱[16]。模拟出12：00列车在各站的上座率，取列车上座率界值C=65%，取弹性系数θ=0.9。利用上述数据与公式（15）即可计算出12：00 各列车在各站点的捎带能力，具体如表4所示。

表4 12：00列车在各站点的捎带能力 单位：箱

续表4

网络售票通道通常在发车前30min关闭，此后列车上座率不会有较大波动，因此取T=30min，并模拟出距离列车到站（始发）的间隔时间为30min时该列车自身的捎带能力情况，受篇幅所限，仅列出部分时刻，如表5所示。

表5 距离列车到站（始发）的间隔时间为30min时列车自身的捎带能力 单位：箱

此外，计算列车在各站的捎带能力时，取弹性系数θ=0.9，这相当于预留了5 箱左右的捎带能力，因此取Q=5箱。另取车站单次装卸作业费用ci=30元/次，车站装卸作业速率ei=25箱/min。

4.2 初始规划阶段

将表2 中的货运需求以及表4 中的捎带能力数据代入初始规划模型，可得到初始静态装运方案，如图3所示。

图3 初始装运方案

4.3 动态调整阶段

（1）确定方案调整时刻

依据图2确定方案调整时刻：

①执行既定装运方案。

②计算出距离各列车到达装运作业站的间隔时间为30min的全部时刻。

③将各时刻按时间顺序依次记录为时刻1，时刻2，…，时刻16，如表6所示。此步骤，h=0。

④h=h+1。

⑤时刻h即12：10，从表5 获取列车D1928 在成都东及其后所有站点捎带能力。

⑥计算D1928 在成都东站及其后所有站点的剩余捎带能力，结果如表6所示。

表6 与各时刻对应的列车的剩余捎带能力 单位：箱

⑦判断D1928 在成都东站的装运作业是否可执行。因可执行，进行步骤⑧。

⑧判断h=n是否成立，因不成立，返回步骤④。

经过两次循环，确定12：21为调整时刻。

（2）装运方案调整

模拟时刻12：21 列车在各站的捎带能力并计算得到剩余捎带能力如表7 所示。计算12：21 列车在各站的剩余可利用停站时长如表8所示。12：21 可调整的装运作业所包含的货物如表9 所示。将以上数据代入装运方案调整模型并利用LINGO求解。

表7 列车在各站的剩余捎带能力 单位：箱

表8 列车在各站的剩余可利用停站时长 单位：min

表9 可调整的装运作业所包含的货物

（3）重复进行步骤（1）（2）直至货物全部被运输。

该过程中，13：32及15：15被确定为调整时刻。经过3次调整，得到最终装运方案，如图4所示。

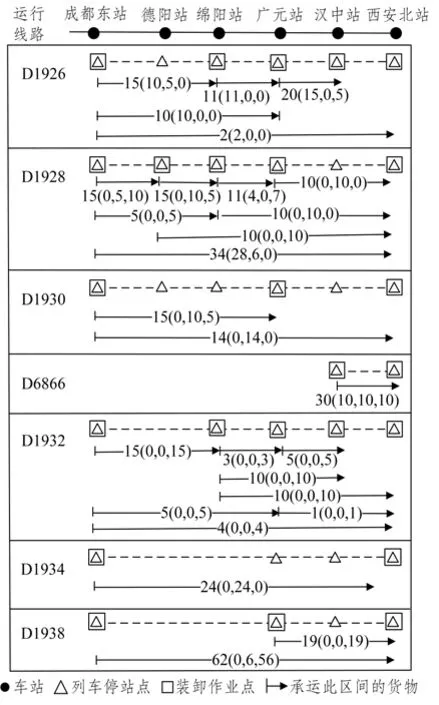
图4 最终装运方案

4.4 运算结果分析

（1）初始与最终装运方案分析

对初始与最终装运方案进行分析，如表10所示。

表10 初始与最终装运方案分析结果

由表10、图3及图4可得：

①初始装运方案与最终装运方案选定相同的7 列列车投入货物运输。这表明，因部分列车捎带能力动态变化而无法满足的货运需求被调整至其余已选定列车满足，并未额外新增列车。

②最终装运方案的货运费用略高于初始装运方案。在列车捎带能力动态变化的情况下，为确保装运作业顺利执行，必须对初始装运方案做出相应调整，由此引起的货运费用的小幅上升是可以接受的。

（2）两阶段规划策略与一般规划策略对比

为验证两阶段规划策略的有效性，与求解列车捎带能力动态变化的一般规划策略相比较。一般规划策略的方案制定与调整步骤为：

①制定初始装运方案。

②初始方案执行过程中，当捎带能力动态变化使货物无法装运时，按货物时效等级由低到高的顺序，从既定装运作业中去掉一定数量的货物直至装运作业可以执行。

③初始方案执行完毕后，汇总所有未能装运货物并再次制定装运方案。

④重复执行②，③步骤直至全部货物被运输完毕。

依据此种策略制定的装运方案如图5所示。

图5 一般规划策略制定的装运方案

对两种规划策略的求解结果进一步对比分析，如表11所示。

表11 两种规划策略对比结果

两种策略都能够在列车捎带能力动态变化的情况下实时调整装运方案，确保装运作业的顺利执行。但相较于一般规划策略，两阶段规划策略使货运费用下降了5.0%，列车数下降了22.2%，两阶段规划策略显著优于一般规划策略。

5 结束语

当前缺少考虑列车捎带能力动态变化的高铁物流装运方案的研究，针对该问题，提出“初始规划+动态调整”的两阶段规划策略。初始规划阶段，构建初始静态装运模型；动态调整阶段，将该阶段划分为若干个静态子阶段，构建装运方案调整模型。案例分析表明：

①两阶段规划策略得到的最终装运方案在货运费用上略高于初始装运方案，但最终方案是为确保装运作业顺利执行，根据列车捎带能力动态变化情况实时调整装运方案的所得结果，因此货运费用的小幅上升是可接受的。

②相较于一般规划策略，两阶段规划策略得到的最终装运方案使货运费用下降了5.0%，列车数下降了22.2%，两阶段规划策略显著优于一般规划策略，可为铁路部门制定高铁物流装运方案提供一定的参考。

随着高铁货运量的不断增长，货物中转运输将成为高铁货运组织工作的重点，可进一步研究考虑货物中转的高铁物流装运方案。