基于里德堡原子的微波电场量子传感

张临杰，景明勇，张好

（1.山西大学 激光光谱研究所 量子光学与光量子器件国家重点实验室，山西 太原 030006；2.山西大学 极端光学协同创新中心，山西 太原 030006）

0 引言

微波是指频率在300 MHz～3 000 GHz（波长约0.1 mm～1 m）范围内的电磁波，微波可用于通信、遥感以及能量传输，在电子信息、航空航天、生物医药、国防安全等领域具有重要应用。目前最为常用的微波电场传感是基于金属偶极子天线在微波电场作用下产生感应电流，通过感应电流的测量获得微波电场的振幅、频率、相位等参数信息。高灵敏、高精度、大带宽的微波传感技术始终是电子信息领域的研究热点。传统的金属偶极子天线的微波测量灵敏度主要受限于Johnson-Nyquist噪声（也被称为热噪声、Johnson噪声或Nyquist噪声）。Johnson-Nyquist噪声是热平衡状态下由于电导体内部的电荷载流子（通常是电子）随机热运动产生的电流噪声。无论电导体两端是否施加电压，此类噪声始终存在，其强度仅依赖于电导体的温度。传统微波测量的信号载体是自由电子，信号和噪声都被编码在电子的宏观运动（电流）中，因此热噪声会导致信噪比的恶化。同时由于天线尺寸决定了宏观电流运动的边界条件，影响了微波电场感应驻波电流的建立，进而影响微波测量的灵敏度和带宽。另外传统天线产生的感应电场对被测微波场扰动较大，不利于高精度测量的实现。上述问题都是传统微波天线无法克服的物理限制。对于基于原子体系的量子测量而言，当微波频率与原子能级间跃迁频率共振时，微波电场与原子发生相干耦合效应。而且原子体系中几乎不存在自由电子，所以基于原子的微波传感不受Johnson-Ny⁃quist噪声的影响。微波电场探测灵敏度主要取决于原子和微波场的相干耦合强度，不依赖于天线尺寸效应。因此，基于原子的量子测量系统在原理上可以克服基于金属偶极天线的传统测量系统所存在的诸多限制。近些年来，基于原子体系的量子精密测量已经在原子钟、光钟［1］和磁场测量［2］领域获得了巨大的成功，光晶格锶原子光钟的秒稳已经优于10-18［3］，基于原子自旋压缩的磁力计测量精度也逼近了标准量子极限的水平，最小可测磁场强度达到fT量级［4］，而基于里德堡原子体系的微波电场量子精密测量与传感正在成为新的研究热点［5］。文献［6］对微波电场的计量、成像等方面研究进展进行了综述。文献［7-8］分别系统地介绍了里德堡原子在毫米、厘米波段以及米波波段微波电场测量的研究进展，以及与传统微波测量技术的比较优势。

本文首先介绍量子传感的定义和概念，对里德堡原子微波传感的研究进展进行简要的回顾，并重点阐述里德堡原子微波电场计、基于缀饰里德堡原子微波超外差接收机以及超冷原子微波电场测量的实验实现和主要结果；最后讨论了里德堡原子微波天线的灵敏度指标提升方面的可行的技术方案。

1 量子传感

Degen等提出，利用具备以下三个特征之一的量子体系进行物理量测量，被称之为量子传感［9］。

（1）具有量子化的、分立的能级结构的系统（如原子、分子、离子等）；

（2）利用量子相干态（可用波函数描述的时间或空间叠加态）来进行物理量的测量；

（3）利用量子纠缠来提高测量的灵敏度或者精度，可超越经典测量的极限。

前面两种类型的量子传感定义相对较为宽泛，可覆盖多种物理系统，前两种类型的系统在技术上更容易实现和推向应用，而基于第三种类型系统的测量和传感则是更为严格意义上的“量子传感”。由于第三种类型的量子传感依赖于多比特纠缠态的实现，可利用最大纠缠态（如两比特Bell态）达到海森堡极限测量。

借助于上述的量子传感定义，典型的量子传感操作过程一般分为以下几步，如图1所示：

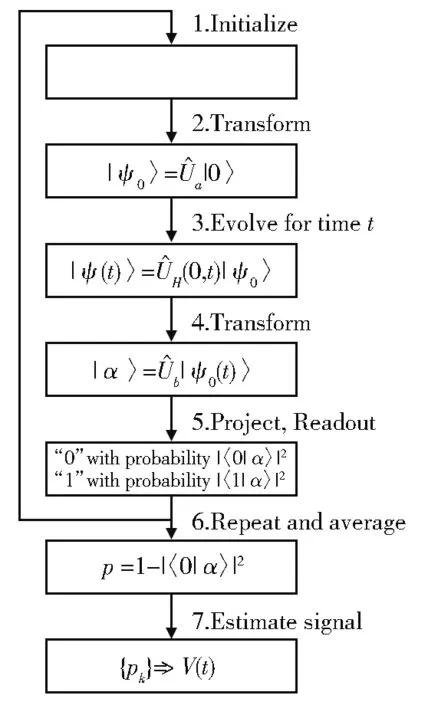
图1 典型量子传感协议流程图［9］Fig.1 Basic protocol of quantum sensing process［9］

（3）在时间段t内，在被测物理量V的作用下，量子初态实现了量子态演化：是两个正交态，c0和 c1是复系数。

（4）通过量子态操作，将量子态变换到可测量的量子终态上：

（5）量子终态被读出，通常量子态读出为投影读取测量。投影读取过程也被称为Ber⁃noulli过程：量子态投影到“0”态的概率为 1-p′，投 影 到“1”态 的 概 率 为 p′，这 里 p′=|c′1|2∝p；

根据不同量子体系的特点，不同类型的量子传感器对某些特定物理量具有特定的响应特性，并且量子传感器具有“本质超灵敏”特性，也就是说量子传感器可以仅对待测的信号进行响应，而对噪声响应较不敏感。目前已在实验室成功演示的量子传感器体系包括：原子、离子、分子、超导比特等，可对时间/频率、重力、位移、加速度、温度、压力以及电磁场等多种类型的物理量实现高灵敏、高精度传感。

2 里德堡原子微波电场计

里德堡原子是指主量子数远大于1的原子，其最外层束缚电子离原子核很远［10］。里德堡原子具有巨大的电偶极矩，因此里德堡原子对外电场响应灵敏；其次，随着里德堡原子主量子数的变化，邻近里德堡态的能级跃迁频率可覆盖MHz—THz的超宽范围。第三，相较于基态原子和低激发态原子，里德堡原子具有更长的辐射寿命，可获得更长的相干测量积分时间，有利于获得更高的相干测量灵敏度。借助于激光频率精确锁定、大范围可调谐等技术的快速发展，利用单光子或多光子激发方式可实现里德堡量子态的精确制备，以及对里德堡量子态的光读出。在超冷原子系统里利用里德堡原子强相互作用的特点，可以实现多比特量子纠缠制备。所以里德堡原子可以完成上述的三种类型量子传感器，适合成为下一代微波电场测量和传感平台。

里德堡原子与微波电场的相互作用分为共振耦合和非共振耦合两种方式。当微波频率与原子能级间跃迁频率相等时，微波电场与里德堡原子的相互作用为共振耦合；当微波频率与原子能级间跃迁频率大失谐时，微波电场与里德堡原子的作用为非共振耦合。基于里德堡原子的微波电场量子传感已经在精度［11］、灵敏度［12］、宽带可调谐性［13］、亚波长分辨率的空间电场特征刻画［14］等方面显示出巨大的潜力。近年来，针对此类传感器的基础研究和工程技术研究均出现了热潮，包括小型化原子天线传感器探头的开发［15］，以及基于里德堡原子微波传感器的雷达基础功能演示：测速演示、到达角测量等［16］。本节着重介绍里德堡原子量子传感的重要应用之一：微波电场计。

2012年，美国与德国研究小组合作首次借助室温铷里德堡原子的电磁诱导透明（Electro⁃magnetically induced transparency，EIT）光谱技术实现了可溯源至普朗克常数的微波电场精密测量［11］。图2（a）所示为实验中使用的铷里德堡原子的能级示意图，在两束波长分别为780 nm（探测光）和480 nm（耦合光）的激光共同作用下，可将碱金属铷原子由基态5S1/2经由中间态5P3/2，两步激发到里德堡态53D5/2。随着耦合光频率调谐到5P3/2-53D5/2共振位置附近时，探测光出现吸收减弱的现象，被称为电磁诱导透明效应，探测光的光谱如图2（b）中最上图所示。

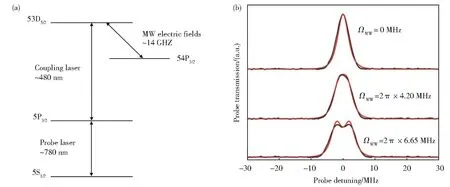
图2 （a）铷原子里德堡态与微波电场作用能级示意图；（b）微波测量时电磁诱导透明光谱变化示意图Fig.2 (a)87Rb atomic energy level structure for the microwave electric field measurement;(b)The splitting of electromagnetic induced transparency spectroscopy with a resonant microwave electric field

里德堡态53D5/2和54P3/2的跃迁频率约为14 GHz，此频率的微波电场可与上述两个里德堡态发生共振相互作用。当微波电场的频率近共振于里德堡态邻近能级跃迁频率时，微波电场的作用相当于在里德堡态邻近能级简化二能级系统中加入了一个微扰。微扰的加入可处理为初始里德堡态本征能量发生了变化ΔEn：

其中ℏ为约化普朗克常量，ΩS为待测信号微波场的拉比频率，

μr为微波电场对应的相邻里德堡态的跃迁偶极距，可以根据里德堡原子能级精确测量值计算获得。ES为待测微波电场的电场强度有效值。由此可看出通过精确测量里德堡原子的能级变化ΔEn，就可由上述表达式精确计算得到被测微波电场场强。图2（b）中无微波电场作用时，电磁诱导透明光谱显示出单峰的结构；当加入近共振的微波电场时，电磁诱导透明光谱呈现出对称分裂；随着微波电场场强的增加，分裂峰的间隔逐渐变大，光谱分裂间隔的大小正比于微波场强。

当微波电场场强较小，其引起的里德堡态能级变化ΔEn小于电磁诱导透明光谱的半高宽ΔEIT，电磁诱导光谱分裂变得不易分辨，如图2（b）中微波电场的拉比频率为4.20 MHz、6.65 MHz情况下EIT光谱所示，此时利用分裂间隔计算场强将存在较大误差，场强的溯源性无法得到很好的保证。

当光谱分裂间隔不可测量时，文献［11］通过测量EIT光谱的峰值高度随微波场强的变化。从图3可以看出，当微波场强较小时，曲线 的 斜 率 逐 渐 变 小 ，最 终 得 到 30 μV·cm-1·Hz-1/2场 强 灵 敏 度 ，8 μV·cm-1最 小 可 探 测 场强。与传统电偶极天线微波电场测量原理不同，基于里德堡原子电磁诱导透明光谱的微波电场测量技术核心是对激光频率的精确测量。由于微波场强的测量值可被溯源至普朗克常数，因此基于里德堡原子的微波电场测量技术在微波场强计量领域具有重大应用潜力。

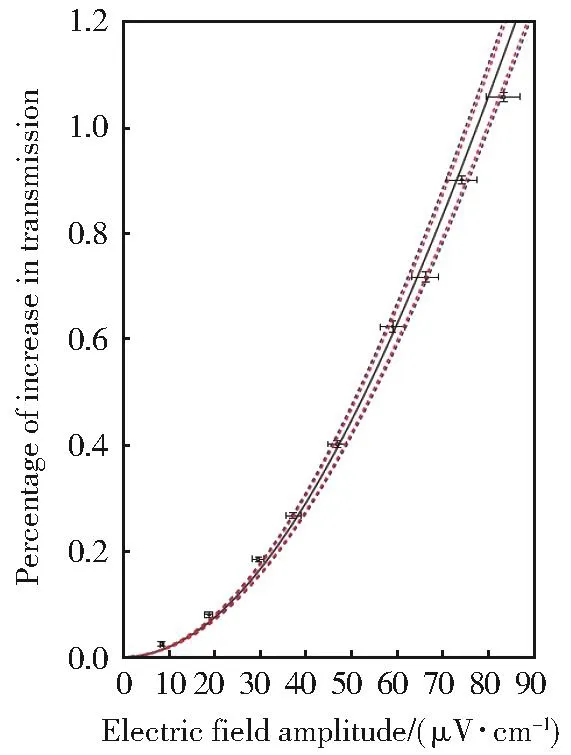
图3 电磁诱导透明光谱透射强度与微波场强的关系［11］Fig.3 Four-level EIT transmission signal as a function of MW electric field amplitude［11］

3 基于缀饰里德堡原子的微波超外差接收机

基于电磁诱导透明光谱的分裂间隔和幅度测量的里德堡原子微波电场计，仅能实现对微波电场的强度和极化方向测量，此外探测灵敏度仅达到μV·cm-1·Hz-1/2量级，因此发展对微波电场的频率、相位、方向等全参数的量子精密测量和传感，特别是进一步提升探测灵敏度，将在态势感知、电子对抗、天文遥感领域具有重大意义。

微波超外差接收机由于具有很大的接收动态范围以及高的接收灵敏度，如今已经被广泛应用于雷达、通信和武器制导系统等需要实现远程信号的接收的领域。图4为传统超外差接收机工作原理图，其核心原理是：利用混频器将被测高频微波信号与本振微波作用，并输出两者的差频信号称为中频信号，然后经中频放大、检波和低频放大等处理，获得被测微波场的有效信息。超外差微波接收机将高频微波信号频率变换为超音频，因此称之为超外差，该原理由E.H.阿姆斯特朗在1918年首次提出。

图4 超外差接收机工作原理示意图Fig.4 Schematic diagram of superheterodyne receiver

2020年，山西大学研究组首次在国际上实现了基于缀饰里德堡原子微波超外差接收机［12］。微波缀饰里德堡原子能级如图5（a）所示，相比于图2所示的里德堡能级示意图增加了一个本振微波场。本振微波电场的加入实现了对里德堡原子态的缀饰，同时在实验上本振微波场与被测微波场的频率较为接近，在一定的响应带宽范围内可以认为通过里德堡原子实现了经典混频器的功能。里德堡原子产生的中频信号映射到电磁诱导透明光谱，再经由光电探测器转换为电信号完成读出。本振微波场的第一个作用是：通过与被测微波场混频，由中频信号可反演出被测微波场的频率和相位信息；中频信号的频率等于被测微波场与本振微波场的频率差。当本振微波场与被测微波场频率相等时，电磁诱导透明光谱强度直接依赖于被测微波场与本振微波场的相对相位差，所以本振微波场的加入使得测量被测微波场频率和相位成为可能。本振微波场的第二个作用是：通过本振微波场拉比频率可以调节微波缀饰里德堡暗态的能级偏置E，从而裁剪微波缀饰里德堡暗态的光谱特性。在特定的本振微波场的拉比频率下，在耦合激光频率共振位置处，微波缀饰里德堡暗态的本征能级微扰可以最大斜率转换成探测光透射强度的变化，同时通过能级对应光谱产生的探测光透射变化具有相同的相位，不会相互抵消，如图5（b）所示。原子超外差测量模型最佳工作点可以由本振微波电场作用下的EIT光谱一阶微分斜率求解，计算得到简化理论模型下的本振微波电场最佳拉比频率：

图5 （a）缀饰里德堡原子超外差接收机能级示意图；（b）本振微波场作用下的EIT光谱［12］Fig.5 (a)Energy levels diagram of Rydberg atoms dressed by microwave electric fields;(b)Engineering EIT spectrum of dressed Rydberg atoms for sensitive MW detection[12]

在原子超外差接收机测量模型中，当被测微波场满足Ωs≪ ΩL时，EIT探测光功率可表示为：

可以看作有效参与微波测量的光功率。τ=1/Γ为系统的相干时间。

由公式（4）可看出，探测光含时振荡信号的幅值正比于信号场的拉比频率，即对信号场的电场强度具有线性响应。

同时探测光含时振荡的频率和相位取决于本振微波场和信号微波场的相对频率和相位，因此，通过测量含时振荡信号，便可以获得信号微波场的全部信息。这里被测微波电场的场强可表示为：

从上式可以看到缀饰里德堡原子超外差机测量的微波场强值，也可以直接溯源到普朗克常数，由此技术发展的原子微波天线可实现自校准。

由于缀饰微波场的加入，极大地提高了里德堡原子系综对微波场响应的内禀增益。利用缀饰里德堡原子超外差接收机可将微波电场的探测灵敏度提高到 55 nV∙cm-1∙Hz-1/2，最小可探测微波场强达到了780 pV∙cm-1。图6所示为基于EIT光谱技术的里德堡原子电场计以及缀饰里德堡原子超外差接收机测量结果的对比。由图6可以看到，利用EIT光谱分裂测量微波电场的曲线在场强值大于0.3 V·m-1时具有较好的线性度；深蓝色方点为基于EIT共振透射实现的原子电场计测量结果，得到的最小探测灵敏度为3 mV·m-1·Hz-1/2。对于缀饰里德堡原子超外差接收机的数据拟合曲线可以看出其测量结果和输入微波场电场强度具有线性关系。在与原子电场计的系统噪声相同的情况下，原子超外差测量系统的信号强度随电场减弱变化更慢，因此能够得到了更高的灵敏度。相较于文献［8］中可溯源里德堡原子电场计得到的灵敏度指标提高了近三个数量级。考虑到缀饰里德堡原子超外差接收机在被测微波场的强度和本振微波场强度接近时才开始出现非线性效应，表明其线性动态范围可以达到90 dB，优于原子电场计约60 dB。

图6 里德堡原子电场计与缀饰里德堡原子超外差接收机探测灵敏度的对比［12］Fig.6 Comparison of atomic electrometer and atomic superhet［12］

4 基于超冷原子体系的微波场测量

随着激光冷却与俘获技术的发展，采用磁光阱技术可得到温度为μK的超冷原子样品，利用蒸发冷却技术可实现低至nK的量子简并原子气体。超冷原子相对于室温下的热原子而言，超冷原子体系的运动速度及速度分布的范围都要低几个量级。随着多普勒效应减弱，光和原子的相干作用时间增加，并且冷原子系综中碰撞概率显著降低，提高原子量子态的退相干时间，增加了有效相干测量时间，这些因素都对有效地改善测量精度和灵敏度有很大帮助。通过在冷原子体系中加入偶极阱或光晶格不仅可以进一步降低碰撞，还可以通过对光晶格确定点位的原子精确寻址和操控，利用里德堡原子长程相互作用实现纠缠原子系综。在原子传感过程中利用N个不相关（非纠缠）原子可以得到的测量标准量子极限（SQL），而纠缠的原子系综可以将测量不确定度提升到海森堡极限∝1/N，实现逼近和突破标准量子噪声极限的测量在相关实验得到验证［17-20］。

2003年，美国研究小组利用微波电场与超冷里德堡原子的相互作用，通过选择场电离光谱技术实现里德堡nS态、nP态和nD态量子亏损的精确测量［21］。图7（a）所示为利用微波双光子共振技术反推85Rb原子里德堡态32D5/2-33D5/2的精确共振跃迁频率结果，随着微波功率变小，理论上由功率引起的频移趋于0。此外值得一提的是文献［19］中根据超冷原子相干性好的特点，利用脉冲微波场序列先后作用在超冷里德堡原子，观察到了微波作用下的原子干涉现象。图7（b）所示为微波频率失谐所引起的原子干涉Ramsey电离光谱。

图7 （a）32D5/2-33D5/2里德堡态能级间隔与微波功率的关系；（b）不同微波频率失谐下的Ramsey光谱［21］Fig.7 （a）Extrapolation of the observed 32D5/2-33D5/2intervals to zero microwave power；（b）Ramsey fringes for the 34d5/2-35d5/2 transition observed using two 2-μs-long microwave pulses with a 15-μs delay between them［21］

2011年，英国研究小组在超冷87Rb原子体系里观察了微波场作用下的超冷里德堡原子电磁诱导透明光谱的Autler-Townes分裂［22］。实验中利用微波电场控制里德堡暗态极子传输的群折射率，改变了光与里德堡原子的非线性响应。图8（a）所示是超冷里德堡原子实验装置图，采用标准的磁光阱和二级冷却技术获得超冷原子系综，利用两束相对传输的480 nm耦合光和780 nm探测光实现电磁诱导透明光谱。在微波电场作用下，冷原子体系的里德堡原子EIT光谱发生Autler-Townes分裂。随着微波电场强度的增加，分裂间隔逐渐增加，如图8（b）所示。

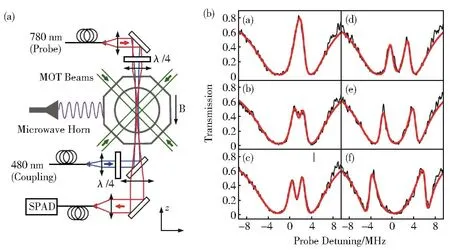
图8 （a）超冷里德堡原子微波电场实验装置示意图；（b）不同微波电场Rabi频率下的里德堡EIT光谱［22］Fig.8 （a）Experimental setup of ultracold Rydberg atoms；（b）Rydberg EIT spectrum versus Rabi frequency of microwave electric fields［22］

2020年，华南师范大学研究小组在超冷原子系统中利用电磁诱导吸收（electromagnetical⁃ly induced absorption，EIA）效应实现了微波电场的自校准测量［23］。图9所示为EIA光谱在不同微波场强下测量的分裂光谱结果。实验证明微波电场拉比频率与EIA光谱的分裂间隔具有很好的线性关系，实现的微波探测灵敏度为 100 μV·cm-1。

图9 不同微波功率下的EIA-AT分裂光谱（a）功率为−26.6 dBm；（b）功率为−12.6 dBm［23］Fig.9 Spectral line fits for two cases in the crossover regime：ATS with MWpower equal to（a）−26.6 dBm，and（b）−12.6 dBm［23］

2016年，法国研究小组报道基于高角动量（J≈ 25）单个圆态里德堡原子的薛定谔猫态实现了突破标准散粒噪声极限的射频电场测量［24］。图10（a）所示是实验中涉及到的能级图，实验中首先制备了里德堡原子圆态，然后利用微波电场实现了单里德堡原子薛定谔猫态的制备。射频脉冲的加入使得里德堡原子能级发生Δm=1的跃迁，也就是将单原子薛定谔猫态附加一定的相位变化，如图10（b）所示。初始里德堡原子圆态在第一个射频脉冲电场作用下在布洛赫球上进行了角度旋转：，经过演化时间态沿着z轴以频率δω= ω（F）− ωrf做进动到目标态，第二个射频脉冲电场进行旋转操作图中显示通过经典Ramsey计算出量子态的相位积累（正比于图中iv球面上的阴影面积）进而得到ΔF。图10（c）中显示了采用如下参数得到的理论仿真结果：射频脉冲宽度为184 ns，脉冲间隔时间τ=56 ns、ΔF=1.7 mV·cm−1。

图10 （a）里德堡圆态射频场测量能级图；（b）射频Ramsey操作导致的量子态在布洛赫球上演化；（c）微波脉冲操作在布洛赫球上的转动示意图［24］Fig.10 Atomic levels and measurement sequence.（a）Energies of the Stark levels in the n=50 and 51 manifold sorted by their magnetic quantum number；（b）Evolution of the J spin in the Ramsey sequence；（c）Simulation in Bloch sphere of a realistic sequence［24］

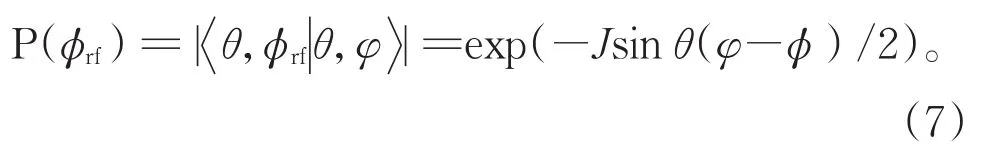
图11（b）中显示了微波场作用下产生薛定谔猫态对射频电场测量的结果。测量得到态的概率与射频场引入相位的关系为：

图11 经典和薛定谔猫态实现的射频测量结果（a）经典Ramsey干涉结果；（b）加入微波场操控的Ramsey干涉结果［24］Fig.11 （a）Simple Ramsey measurement；（b）Ramsey measurement including the microwave pulses［24］

这里Φ依赖于射频场引入的相位ϕrf。

利用里德堡原子圆态制备的薛定谔猫态实现的微波高灵敏测量，积分时间200 ns内得到的单次探测灵敏度（single-shot sensitivity）达到了1.2 mV∙cm-1。考虑到实验的时序时间因素，对 应 的 1 s 探测 灵 敏 度 达到 30 μV∙cm-1·Hz1/2。然而，由于参与测量的有效原子数限制，基于超冷原子体系获得微波测量绝对灵敏度通常不能直接与热原子体系得到的结果进行比较。

5 基于里德堡原子微波量子传感的灵敏度

基于里德堡原子微波量子传感的探测灵敏度如何进一步提升，特别是利用室温原子能否超越传统天线的Johnson-Nyquist噪声灵敏度极限已经成为本领域最重要的研究焦点之一。根据上述章节的介绍，基于里德堡原子微波量子传感的机理是微波电场与里德堡原子能级的相干耦合，利用电磁诱导透明光谱技术对里德堡原子量子态演化进行读出。在进行量子态测量时，当测量时间大于原子体系的退相干时间T2，相关测量时间Tmeas由T2决定。在测量时间内可进行的独立测量数设为N=NaTint/T2，其中Tint为总积分时间，假定每个里德堡原子都在T2时间内参与测量，Na为参与测量的里德堡原子平均数目。原子天线的理论散粒噪声极限可表示为：

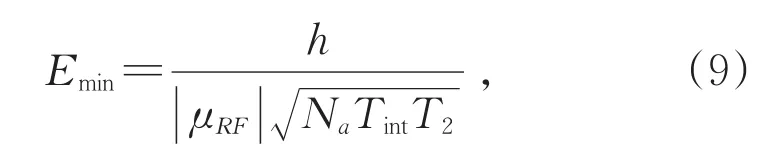
这里h是普朗克常数，μRF是微波场的跃迁偶极矩。

里德堡原子数Na主要受到里德堡激发过程中原子相互作用引起的激发阻塞效应的影响，特别是随着原子主量子数的增加，激发阻塞半径增加变快，限制了最终里德堡原子的数量。在热原子系综中，由于原子多普勒效应的存在，会部分抵消激发阻塞的影响。在冷原子样品中，一般采用绝热消除退相干时间短的中间态方案以及采用激光啁啾频率等方式增加里德堡原子的制备效率。

退相干时间T2在热原子系综中主要由原子进出光束导致的渡越展宽效应影响，其大小决定于原子池的温度、蒸气压以及光束的大小［25］。在冷原子样品中，退相干时间主要由里德堡原子量子态寿命决定。同时黑体辐射效应［26-27］、原子间相互作用的碰撞［28-29］以及超辐射效应［30］都会引起量子态的退相干，这些效应主要依赖于原子的主量子数、角量子数以及原子温度以及密度。

此外在量子态光读出机制下，激光的频率、振幅以及相位噪声等都是限制测量灵敏度的主要因素。采用非经典光场，压缩光的振幅或者相位正交分量，有助于突破光子散粒噪声的限制，提高探测灵敏度［31-33］。影响测量光读出测量灵敏度的其他因素还包括光电探测器和低噪声放大器等电子器件的噪声水平以及探测器带宽。

同时影响探测灵敏度的因素还需要考虑原子蒸汽池对微波测量的影响，包括原子蒸汽池的材料、几何尺寸对微波场扰动［34-35］。利用特殊材料的内壁涂层的原子蒸汽池，可以有效减小原子与蒸汽池内壁的碰撞退相干效应，更好地保护自旋量子态，已经在高灵敏磁场量子传感领域获得很好的应用［36-37］。

6 结论

本文主要综述了量子传感的基本定义和操作，重点介绍了微波量子传感研究中具有一定代表性的工作：里德堡原子微波电场计、基于缀饰里德堡原子微波超外差接收机以及超冷原子微波电场测量实验方案和主要结果。最后讨论了影响里德堡原子微波量子传感探测灵敏度的主要因素和灵敏度水平提升技术方案。