基于样本信息的振动能量采集系统的响应预测

刘迪，刘晓婷，李晶

（1.山西大学 数学科学学院，山西 太原 030006；2.太原科技大学 应用科学学院，山西 太原 030024）

0 引言

近年来，振动能作为绿色可再生的清洁能源受到了许多学者的广泛关注。振动能量采集系统是由一个机械振动系统耦合一个电路系统构成，实现了将环境中的机械能转化为电能，进而为低功率的小型便携设备供电。目前，振动能量采集系统的转换机制主要有三种，分别是压电［1］，电磁［2］，和静电［3］，其中压电和电磁振动能量采集系统由于具有结构简单和能量密度高等优点受到了广泛的研究。

在早期的研究中，研究者主要关注结构频率简单的线性振动能量采集系统的动力学响应［4-6］。而现存环境中的振动源的频率大多复杂多变，因而为了可以有效地捕获环境中的这些振动能，研究者将非线性结构引入到能量采集装置中。根据非线性振动能量采集系统的结构特征，可以分为单稳态［7］、双稳态［8］和多稳态［9］系统。众所周知，随机激励系统存在于现实环境中且可激发复杂的动力学行为。因此，为了理解其对能量采集性能的影响，一些随机方法被发展，用于研究随机作用下模型结构和采集性能之间的关系。例如，Zhou等［10］利用谐波平衡法研究了系统参数对非线性三稳态能量采集系统动态响应的影响，并发现该结构可以提高低水平环境激励下能量采集性能。Wang等［11］使用细致平衡法研究了高斯白噪声激励下具有非对称势能的多稳态能量采集器的随机响应特性。此外，Jin等［12］利用多尺度方法得到了窄带随机激励下的迟滞双稳态系统在主共振附近的稳态响应解析表达式及其稳定的条件。

Shannon信息熵描述了与随机变量相关的全局不确定性，并量化了与随机现象相关的信息内容。最大熵原理是在约束条件下，通过求解最大熵函数来确定未知的概率分布［13］。它可以实现在已知部分信息的情况下推断出未知的分布，因而得到了广泛的应用［14-15］。对于描述随机现象的系统，Trebicki等［16］利用最大熵方法，在矩约束条件下求解平稳概率分布。接着，Ricciardi等［17］基于最大熵原理建立一种局部随机线性化方法。随后，Tian等［18］利用最大熵原理和机器学习获得了系统响应的平稳概率密度函数。

在上述研究的基础上，本文基于系统响应过程的样本信息，利用最大熵原理提出了一种基于部分响应信息的响应概率密度函数预测方法，并详细研究了单稳态，双稳态及三稳态非线性振动能量采集系统的随机响应。本文结构如下：第1节提出了基于样本信息预测响应概率密度函数的理论方法，利用Euler-Maruyama方法得到随机系统的响应信息，进而得到高阶中心矩信息，在此基础上，使用最大熵原理和高阶中心矩信息对响应概率密度函数进行预测。第2节中介绍了三种不同结构势函数的振动能量采集系统，并应用上一节所提出方法得出了概率密度函数的解析表达式，然后使用直接蒙特卡洛模拟验证了所提出方法的有效性。最后给出相关结论。

1 基于响应过程信息的概率密度预测

本文将提出一种基于随机非线性振动能量采集系统样本信息的稳态响应概率密度函数的预测方法，并将其应用到三种不同非线性结构随机系统中。

1.1 非线性振动能量采集系统的数学模型及样本信息

考虑一类质量为M的机电耦合的振动能量采集系统，其耦合方式主要分为压电式或电磁式，相应地数学模型可以表示为：

最后，利用多目标粒子群（PSO）算法，通过求解式（12）的最优解，得到拉格朗日乘子λk，进而获得响应过程的概率密度函数。在下一节中，我们通过三种不同结构的随机振动能量采集系统验证上述方法的有效性。

2 三种不同非线性结构随机系统的概率密度函数预测

假设振动能量采集系统（2）的势函数U(X)具有如下一般形式解

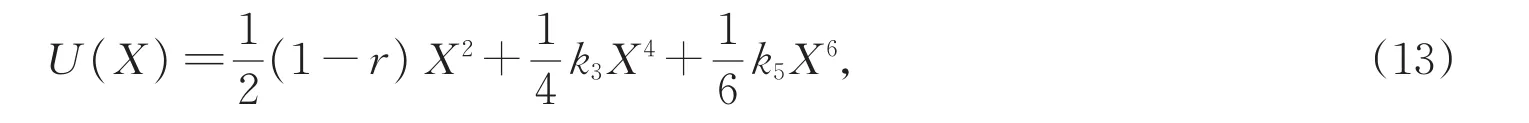
这里参数r，k3和k5的不同组合可以形成三种不同的势函数，如图1所示，其中图1（a）中的蓝色，绿色和黄色分别表示单稳态，双稳态和三稳态势函数。随后，给定参数r和k5的情况下，图1（b−d）展示了势能函数随参数k3的变化，并用红线标出相应势函数的稳态点变化。当r=0，k5=1时，稳态点个数从1到3，当r=1，k5=1时，稳态点的个数从1到3，而r=2，k5=1时，只有两个稳态点。观察式（13），可以发现势函数的最高次幂为六次，并且对于最大熵原理，我们在已知系统前8阶中心矩的情况下，基本可以准确预测出系统响应的概率密度函数。因此在下面的研究中，我们分别基于单稳态，双稳态和三稳态势函数的前8阶样本中心矩信息，利用多目标PSO算法预测相应的概率密度函数。

2.1 非线性单稳态振动能量采集系统的概率密度函数预测

在这种情况下，我们在图1（a）中的蓝色区域任意选取一个点，即r=−1，k3=−4.6，k5=4。利用Euler-Maruyama方法，我们可以分别得到5 000个系统（2）三个响应过程X，Ẋ和Y的样本点信息，如图2所示，基于这些样本点信息，由式（5）获得各响应过程的前8阶样本中心矩信息，通过求解优化问题（12），进而计算得到响应过程的概率密度函数（10）的拉格朗日乘子。此时，三个响应过程的概率密度函数的解析表达式分别为

图1 （a）稳定点个数与参数的关系；（b）当r=0，k5=1时，稳态点个数的变化；（c）当r=1，k5=1时，稳态点的个数的变化；（d）当r=2，k5=1时，只有两个稳态点Fig.1 (a)Relationship between the number of steady points and parameters;(b)Change of steady state points whenr=0and k5=1;(c)Change of steady state points whenr=1andk5=1;(d)Whenr=2andk5=1,there are only two steady state points

图2 单稳态能量采集系统的响应样本信息。（a）位移X，（b）速度dX/dt，（c）感应电压YFig.2 Response samples information of monostable energy harvesting system.（a）Displacement X；（b）Velocity dX/dt；（c）Induced voltage Y

随后，通过直接蒙特卡洛数值模拟法验证了预测解（14）的准确性，图3展示了预测解与直接蒙特卡洛数值模拟对比的结果，其中蓝色的实线和红色的星号分别表示由式（14）和直接蒙特卡洛数值模拟所获得的结果。通过对比，我们发现它们之间存在很高的一致性。通过观察式（14）中响应过程 X 的概率密度函数的拉格朗日乘子，可以发现其中|λ2|，|λ4|和|λ6|远大于其他|λi|，是概率密度函数的主要部分，这与势函数中的系数r，k3，k5≫0一致，而其他λi较小则是由多目标PSO算法求解目标函数（12）的误差引起的。

图3 预测结果和直接蒙特卡洛模拟结果的比较。（a）位移X，（b）速度dX dt，（c）感应电压YFig.3 Comparison between predict results and direct Monte Carlo results.（a）DisplacementX；（b）VelocitydX dt；（c）Induced voltageY

2.2 非线性双稳态振动能量采集系统的概率密度函数预测

为了进一步验证方法的有效性，我们预测双稳态振动能量采集系统响应过程的概率密度函数。在这种情况下，我们在图1（a）中的绿色区域任意选取一个点，即r=2，k3=−4.6，k5=3。同样利用Euler-Maruyama方法，我们可以分别得到5 000个双稳态系统（2）的三个响应过程X，Ẋ和Y的样本点信息，如图4所示，基于这些样本点信息，利用式（5）计算获得各响应过程的前8阶样本中心矩信息，并通过求解优化问题（12），进而计算得到响应过程的概率密度函数（10）的拉格朗日乘子。此时，预测的三个响应过程的概率密度函数的解析表达式分别为

图4 双稳态能量采集系统的响应样本信息。（a）位移X，（b）速度dX/dt，（c）感应电压YFig.4 Response samples information of bistable energy harvesting system.（a）Displacement X；（b）Velocity dX/dt；（c）Induced voltage Y

随后，通过直接蒙特卡洛数值模拟验证预测结果式（15）的准确性，图5展示了预测结果与直接蒙特卡洛数值模拟对比的结果，其中蓝色的实线和红色的星号分别表示由式（15）和直接蒙特卡洛数值模拟所获得的结果。通过对比，我们发现在双稳态情况下存在很好的一致性，同时响应过程X的概率密度函数具有双峰，这与相应的势函数存在2个稳态点相对应。此外，通过观察式（15）中响应过程X的概率密度函数的拉格朗日乘子，可以发现其中|λ2|，|λ4|和|λ6|同样是概率密度函数的主要部分，其他|λi|≪1，它们是由多目标PSO算法求解目标函数（12）的误差引起的。

图5 分析结果和直接蒙特卡洛模拟结果的比较。（a）位移X，（b）速度dX dt，（c）感应电压YFig.5 Comparison between analytical results and direct Monte Carlo results.（a）DisplacementX；（b）VelocitydX dt；（c）Induced voltageY

2.3 非线性三稳态振动能量采集系统的概率密度函数预测

最后，我们预测更为复杂的三稳态振动能量采集系统的概率密度函数，我们在图1（a）中的黄色区域任意选取一个点，即r=0，k3=−4.6，k5=3。同样利用Euler-Maruyama方法，可以分别获得5 000个三稳态系统（2）的响应过程X，Ẋ和Y的样本点信息，如图6所示，基于这些样本点信息，利用式（5）计算获得各响应过程的前8阶样本中心矩信息，并通过求解优化问题（12），进而计算得到三稳态响应过程的概率密度函数（10）的拉格朗日乘子。此时，相应的概率密度函数的解析表达式分别为

图6 三稳态能量采集系统的响应样本信息。（a）位移X，（b）速度dX/dt，（c）感应电压YFig.6 Response samples information of tristable energy harvesting system.（a）DisplacementX；（b）Velocity dX dt；（c）Induced voltageY

通过直接蒙特卡洛数值模拟法验证预测解式（16）的准确性，图7展示了预测结果与直接蒙特卡洛数值模拟对比，其中蓝色的实线和红色的星号分别表示由式（16）和直接蒙特卡洛数值模拟所获得的结果。通过对比，我们发现响应过程的概率密度函数存在一致性，同时响应过程X的概率密度函数具有三个峰，这与相应的势函数存在3个稳态点相对应。通过观察式（16）中响应过程X的概率密度函数的拉格朗日乘子，同样可以发现|λ2|，|λ4|和|λ6|是概率密度函数的主要部分，但其他|λi|是O(10−1)的同阶或高阶无穷小，它们同样是由多目标PSO算法求解目标函数（12）的误差引起的，但是它们相对于前两种情况偏大，这就意味着三稳态情况下的概率密度函数的预测结果相对另外两种情况较差。这就意味着，系统的结构越复杂，所需要的预测信息也就越多。

图7 分析结果和直接蒙特卡洛模拟结果的比较。（a）位移X，（b）速度dX dt，（c）感应电压YFig.7 Comparison between analytical results and direct Monte Carlo results.（a）DisplacementX；（b）VelocitydX dt；（c）Induced voltageY

3 结论

本文提出了一种基于非线性能量采集系统响应过程样本信息的响应概率密度函数预测方法。首先，利用Euler-Maruyama方法得到随机系统响应样本信息，进而得到各响应样本的高阶中心矩信息。其次，利用最大熵原理预测得到响应过程的概率密度函数的表达式，并在此基础上与高阶中心矩信息结合，将响应过程的概率密度函数的预测问题转化为求解多目标函数最小值的优化问题，并通过多目标粒子群优化算法确定了概率密度函数的表达式。最后，分别以高斯白噪声激励下具有单稳态，双稳态，三稳态结构的振动能量采集系统的高阶中心矩信息为例，得到了相应地概率密度函数的表达式，并用直接蒙特卡洛模拟进行了验证。通过分析发现，概率密度函数指数部分的系数与势函数的系数密切相关，而概率密度函数的部分指数系数较小是因为计算优化函数时的误差所引起的，同时发现结构越简单，在同样信息的条件下预测效果越好，因此对于结构复杂的非线性随机系统，将需要更多的样本信息去提高预测精度。