固定优先级混合关键偶发任务能耗感知算法
张忆文 高振国 林铭炜
1(华侨大学计算机科学与技术学院 福建厦门 361021) 2(福建师范大学数学与信息学院 福州 350117)
随着处理器技术和计算机技术的快速发展,嵌入式系统的发展趋势是将多个不同关键层次的应用集中到同一共享平台形成混合关键系统,以满足时限、功耗与体积的需求.目前,混合关键系统的应用比较广泛,例如航空领域、汽车和工业标准[1](IEC 61508,DO-178B DO-178C,ISO 26262).无人机就是混合关键系统的典型应用.无人机的任务按照属性可以分为安全关键功能和任务关键功能,而安全关键功能必须通过认证.由于无人机等混合关键系统采用电池供电,因此能耗成为设计混合关键系统的重要目标.
目前,混合关键系统的研究已经吸引了广大研究者的兴趣;而这些研究者大多数都关注混合关键系统调度可行性分析方面.Vestal[2]最早研究混合关键系统的调度问题并且分析偶发任务模型的调度可行性.随后,Baruah等人[3]提出了2种有效的混合关键偶发任务调度算法.这2种算法分别为静态混合关键(static mixed criticality, SMC)调度和可适应的混合关键(adaptive mixed criticality, AMC)调度.SMC算法和AMC算法主要区别在于系统处于高模式时,对低关键层次任务的处理.SMC算法在系统处于高模式时,允许部分低关键层次任务执行,而AMC算法舍弃所有的低关键层次任务.Davis等人[4]扩展了SMC和AMC算法,考虑系统模式切换和上下文切换的开销.
文献[2-4]的研究工作主要针对固定优先级系统.Baruah等人[5]最早研究动态优先级混合关键偶发任务的调度问题,并且提出基于虚拟截止期限的最早截止期限优先(earliest deadline first-virtual deadline, EDF-VD)算法.EDF-VD算法在系统处于高模式时,放弃所有低关键层次任务.Liu等人[6]提出一种新的混合关键偶发任务模型即非精确混合关键(imprecise mixed criticality, IMC)任务模型.此外,基于利用率和时间需求分析的方法被用来分析IMC模型.Chen等人[7]提出可行混合关键(flexible mixed criticality, FMC)调度模型,该模型中混合关键偶发任务的最小释放时间可变.此外,Chen等人[7]提出一种基于EDF-VD的利用率分析方法调度混合关键偶发任务.这些研究中,系统处于高模式时,所有的低关键层次任务都将不执行.Su等人[8]研究弹性的混合关键(elastic mixed criticality, E-MC)偶发任务模型且提出最早释放最早截止期限优先(earliest releases-earliest deadline first, ER-EDF)算法.该算法在系统处于高关键模式时,允许执行部分低关键层次偶发任务.
动态电压频率调节(dynamic voltage frequency scaling, DVFS)是降低系统能耗的主要技术,很多研究者将实时调度理论与DVFS技术结合起来解决系统的能耗问题,但这些研究工作主要针对传统的嵌入式系统[9-15].近来,有些研究者开始关注混合关键系统能耗感知调度问题.Huang等人[16]最早研究混合关键偶发任务的能耗感知问题,提出基于EDF-VD能耗感知算法,该算法没有利用高关键层次偶发任务预留的空闲时间.Ali等人[17]扩展了Huang等人[16]的研究成果,提出不仅能够利用静态空闲时间,而且还能利用高关键层次偶发任务预留的空闲时间降低能耗的算法.文献[4,18]针对动态优先的混合关键系统提出动态利用率更新算法,该算法能够动态利用偶发任务产生的空闲时间,进一步降低系统能耗.然而,这些研究工作在系统处于高模式时,将所有低关键层次任务直接舍弃.Sruti等人[19]针对精确混合关键任务模型,结合DVFS技术,提出基于利用率分析的能耗感知算法.该算法在系统处于高模式时,通过减少低关键层次任务的服务速率来降低系统能耗,而不是简单地将所有低关键层次任务舍弃.文献[16-19]研究工作的重点在于系统的能耗与实时性,Jiang等人[20]研究混合关键系统软实时任务的可靠性与能耗感知问题,通过软实时任务执行时间服从随机分布的特点,提出动态编程最优算法.此外,Safari等人[21]研究混合关键双处理器系统的可靠性感知调度问题,提出一种新的可靠性感知能耗管理算法,该算法通过减少低关键层次任务的服务速率来提高系统可靠性.
通过文献[16-21]的调研发现,现有的混合关键能耗感知算法主要关注动态优先级混合关键系统的偶发任务调度问题,很少有研究者关注固定优先级混合关键系统偶发任务的能耗感知调度问题.此外,现有的研究工作没有利用偶发任务到达时间不确定产生的空闲时间,空闲时间的利用率低,导致节能效果不佳.
1 系统模型
1.1 混合关键偶发任务模型
在单处理器系统上考虑相互独立的混合关键偶发任务集Γ,该任务集由n个偶发任务组成即Γ={τ1,τ2,…,τn},每个偶发任务τi(1≤i≤n,i为整数)由五元组{Ti,Di,Li,Ci(LO),Ci(HI)}表示.其中,Ti是τi的最小释放时间;Di是τi的相对截止期限;Li是τi的关键层次,其可以表示为Li={LO,HI};Li的取值为LO代表τi是低关键层次任务,其不需要进行安全认证;Li的取值为HI代表τi是高关键层次任务,其需要进行安全认证;Ci(LO)和Ci(HI)分别表示τi低模式和高模式的最坏情况执行时间.本模型中,混合关键系统的低模式是指系统既执行低关键层次偶发任务又执行高关键层次偶发任务且不需要进行安全认证;混合关键系统的高模式是指系统只执行高关键层次偶发任务且需要进行安全认证.考虑τi具有隐性的截止期限,即其相对截止期限等于最小释放时间,即Di=Ti.低关键层次偶发任务τi的高模式和低模式最坏情况执行时间相等,即Ci(HI)=Ci(LO);高关键偶发任务τi高模式最坏情况执行时间大于或者等于低模式最坏情况执行时间,Ci(HI)≥Ci(LO);这个假设是合理的,因为系统处于高模式时,高关键层次任务需要进行安全认证.此外,假设任务的执行时间与处理器速度为线性关系,即以速度S执行,其执行时间变为Ci(LO)/S.令τij表示偶发任务τi的第j个任务实例.
系统的执行过程为:τi以速度S完成执行且其执行时间大于Ci(LO)/S但不超过Ci(HI)/S时,系统处于高模式;τi以速度S完成执行且其执行时间超过Ci(HI)/S时,系统存在错误行为;τi以速度S完成执行且其执行时间不超过Ci(LO)/S时,系统处于低模式;开始时,系统处于低模式;一旦发现τi以速度S执行,且其执行时间超过Ci(LO)/S时,系统立即切换到高模式;系统处于高模式时,所有高关键层次任务完成执行或者系统处于空闲状态时,返回到低模式.
调度正确标准为:考虑相互独立的混合关键偶发任务集Γ={τ1,τ2,…,τn},算法调度该任务集可行必须满足2个条件:
1) 系统处于低模式时,所有任务以速度S执行,必须在其相应的截止期限内完成执行,且其执行时间不超过Ci(LO)/S.
2) 系统处于高模式时,低关键层次任务全部被丢弃,只执行高关键层次任务;此外;所有高关键层次任务以速度S执行,必须在其相应的截止期限内完成执行,且其执行时间不超过Ci(HI)/S.
1.2 能耗模型
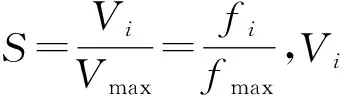
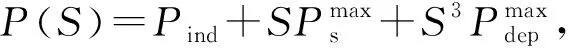
(1)
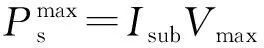
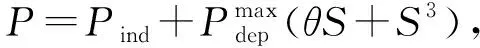
(2)
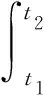
2 关键层次单调速率调度
传统的嵌入式调度策略例如单调速率(rate monotonic, RM)策略和最早截止期限优先(earliest deadline first, EDF)策略调度混合关键偶发任务效率低下,甚至产生不可行的调度[5].为了提高混合关键任务的调度效率,充分利用系统资源,借鉴文献[3]的调度策略,提出关键层次单调速率调度策略(criticality rate monotonic scheme, CRMS).CRMS是固定优先级调度策略,其分配优先级的规则为:1)根据任务的关键层次分配优先级.关键层次越高,其优先级越高;关键层次越低,其优先级越低.2)相同关键层次的任务,按照RM策略分配优先级.最小释放时间越小,其优先级越高;最小释放时间越大,其优先级越大.CRMS分配任务的优先级规则简单、容易操作,且开销小;更重要的是使用该调度策略调度混合关键任务,低关键层次任务出错不会影响到高关键层次任务的执行.
尽管存在一些特例使得CRMS出现优先级反转问题,导致其不是单纯的RM调度.例如存在一个高关键层次任务τ1和低关键层次任务τ2,但τ1的最小释放时间间隔大于τ2,导致最小释放时间间隔大的τ1的优先级大于τ2.通过将高关键层次τ1划分为若干虚拟任务,使得每个虚拟任务的最小释放时间都小于τ2的最小释放时间,且这些虚拟任务的利用率之和等于τ1的利用率.通过虚拟任务的构建,可以避免CRMS中出现优先级反转问题,使得CRMS是完全的单调速率调度.
介绍CRMS调度可行的充分条件之前,先介绍一些概念.
(3)
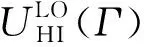
定理1.系统处于低模式时,CRMS调度混合关键偶发任务集Γ调度可行的充分条件为
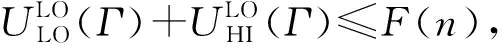
(4)
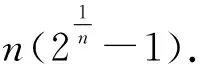
证明.CRMS是固定优先级调度策略,其优先级根据任务的关键层次和RM策略进行分配.如果CRMS调度混合关键偶发任务集Γ是可行的,其必须满足单处理器抢占式RM策略的可信特征[22].CRMS策略在系统处于低模式时,任意τi的执行时间都不超过Ci(LO).从RM策略调度可行的充分条件可知[23],系统处于低模式时,式(4)是CRMS调度混合关键偶发任务集Γ调度可行的充分条件.
证毕.
定理2.系统处于高模式时,CRMS调度混合关键偶发任务集Γ调度可行的充分条件为
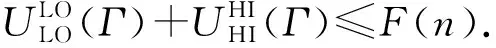
(5)
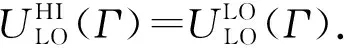
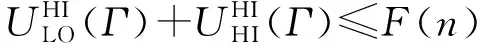
(6)
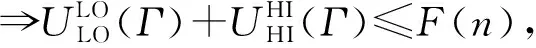
(7)
所以,系统处于高模式时,式(5)是CRMS调度混合关键偶发任务集Γ调度可行的充分条件.
证毕.
推论1.系统处于低模式时,CRMS以速度S1调度混合关键偶发任务集Γ调度可行,则速度S1需要满足:

(8)
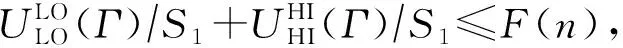
证毕.
推论2.系统处于高模式时,CRMS在低模式和高模式分别以速度S2和最大处理器速度Smax(归一化处理,Smax=1)调度混合关键偶发任务集Γ调度可行,则速度S2需要满足:
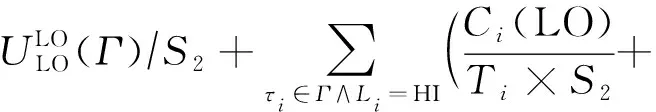
(9)
证明.系统开始处于低模式,低关键层次任务以速度S2;只有高关键层次任务在低模式以速度S2执行且其执行时间超过Ci(LO)/S2,系统才进入高模式;进入高模式之后所有低关键层次任务都被丢弃.而高关键层次任务τi在进入高模式之后以最大处理器速度Smax=1执行,所以其执行时间可以分为2个部分Ci(LO)/S2+(Ci(HI)-Ci(LO))/Smax,其利用率变为Ci(LO)/(S2×Ti)+(Ci(HI)-Ci(LO))/Ti,因此将其带入式(5),进而得出式(9).
证毕.
从推论1和推论2可以直接得到推论3.
推论3.CRMS在低模式和高模式分别以速度S和Smax调度混合关键偶发任务集Γ,调度可行,则速度S需要满足:
S=max{S1,S2}.
(10)
3 混合关键偶发任务能耗感知算法
3.1 研究动机和问题阐述
混合关键系统的能耗感知调度问题受到一些研究者的关注[16-18,24-25].然而,这些研究者主要关注动态优先级混合关键偶发任务能耗感知调度,这些研究成果不能直接应用于固定优先级混合关键系统且这些研究成果空闲时间利用率不足,导致节能效果差.此外,目前的研究工作假设偶发任务以其最小释放时间释放任务实例;然而,偶发任务的到达时间是不确定的,这必然导致系统产生大量空闲时间.通过表1的任务集来解释现有研究的空闲时间利用率低、节能效果差.
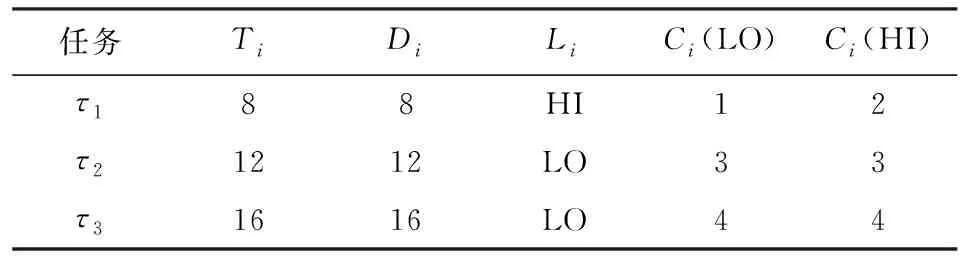
Table 1 Mixed Criticality Sporadic Tasks Set Γ表1 混合关键偶发任务集Γ
假设τ1在时刻0,11,20,32,44释放任务实例;τ2在时刻0,14,28,40释放任务实例;τ3在时刻0,18,34释放任务实例.假设处理器提供的速度范围为[0.3,1],能耗感知算法在区间[0,48]内调度混合关键偶发任务集Γ.通过实例来解释现有能耗感知调度算法空闲时间利用率不高,节能效果不佳.
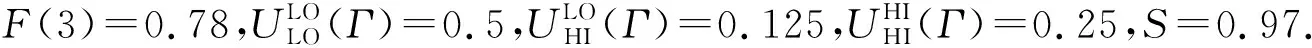
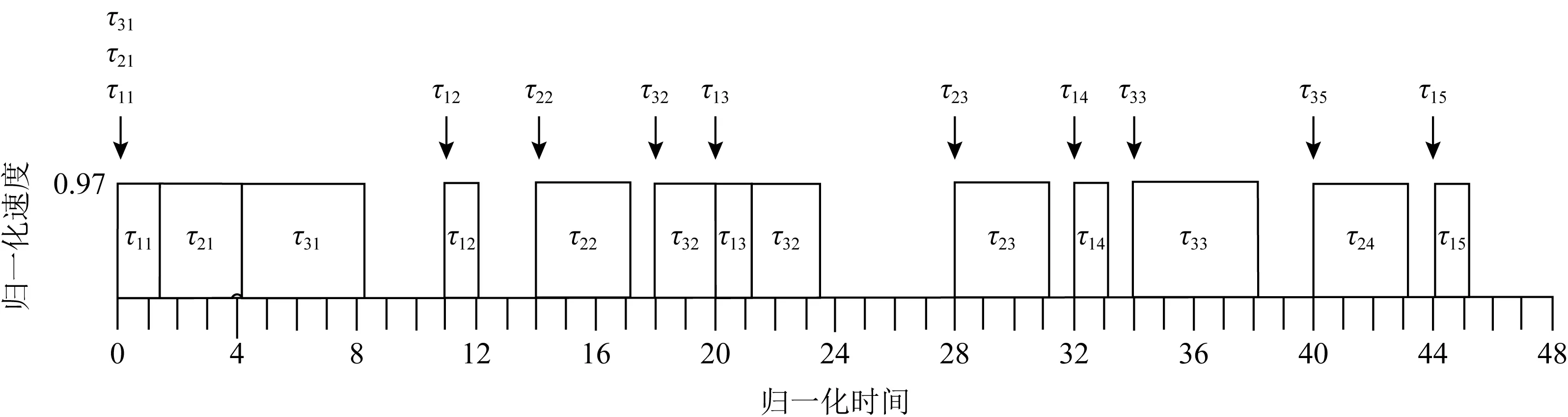
Fig. 1 CRMS algorithm schedules mixed criticality sporadic tasks Γ in low mode图1 CRMS算法在低模式调度混合关键偶发任务集Γ
图1中黑色箭头代表任务实例的到达时间,τ1的优先级最高,τ2的优先级次之,τ3的优先级最低.τ1在时刻0以速度0.97开始执行且在时刻1.03完成执行.在时刻1.03,τ2以速度0.97开始执行且在时刻4.12完成执行.τ3在时刻4.12以速度0.97开始执行且在时刻8.24完成执行.在时刻11,τ1以速度0.97开始执行且在时刻12.03完成执行.τ2在时刻14以速度0.97开始执行且在时刻17.09完成执行.τ3在时刻18开始以速度0.97执行,在时刻20被τ1抢占;τ1在时刻21.03完成执行.τ3恢复执行且在时刻23.15完成执行.剩余的偶发任务以相似的方法调度,不再赘述.
高关键层次空闲时间回收(reclaim high-criticality slack-time, RHS)算法[17]为:文献[17]提出基于动态优先级能耗感知调度算法,该算法不仅能够利用系统的静态空闲时间,而且还能够利用高关键层次任务预留的空闲时间.现将文献[17]提出的算法拓展到固定优先级系统.RHS算法基于CRMS调度混合关键偶发任务集Γ且能够利用高关键层次偶发任务预留的空闲时间.系统处于低模式时,偶发任务开始以速度S(式(10))执行;当高关键层次偶发任务完成执行时,改变处理器速度进一步降低能耗.系统处于高模式时,高关键层次偶发任务以最大处理器速度Smax执行;系统处于低模式时,RHS算法调度混合关键偶发任务集Γ的结果如图2所示.
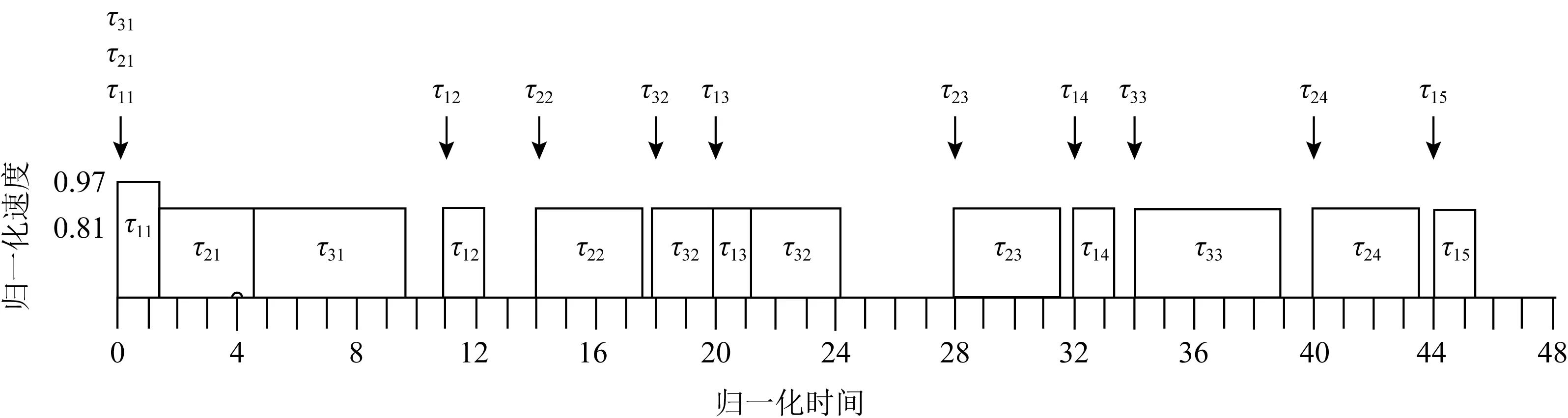
Fig. 2 RHS algorithm schedules mixed criticality sporadic tasks Γ in low mode图2 RHS算法在低模式调度混合关键偶发任务集Γ
图2中黑色箭头代表任务实例的到达时间,τ1在时刻0以速度0.97开始执行且在时刻1.03完成执行.RHS算法利用高关键层次偶发任务τ1预留的空闲时间调节处理器速度.在时刻1.03,τ2以速度0.81开始执行且在时刻4.73完成执行.τ3在时刻4.73以速度0.81开始执行且在时刻9.67完成执行.在时刻11,τ1以速度0.81开始执行且在时刻12.23完成执行.τ2在时刻14以速度0.81开始执行且在时刻17.70完成执行.τ3在时刻18开始以速度0.81执行,在时刻20被τ1抢占;τ1在时刻21.23完成执行.τ3恢复执行且在时刻24.17完成执行.剩余的偶发任务以相似的方法调度,不再赘述.
从图1中可以看出存在大量的空闲时间区间如[8.24,11],[12.03,14],[17.09,18],[23.15,28],[31.09,32],[33.03,34],[38.12,40],[43.09,44],[45.03,48].在图2中依然存在大量的空闲时间区间如[9.67,11],[12.23,14],[17.70,18],[24.17,28],[31.70,32],[33.23,34],[38.94,40],[43.70,44],[45.23,48].产生这些空闲时间的主要原因是偶发任务释放任务实例的时间存在不确定且都大于其最小释放时间,而所计算的能耗感知速度假设偶发任务以其最小释放时间释放任务实例,导致任务的真实利用率低于计算能耗感知速度所使用的利用率.因此,可以利用这些空闲时间进一步降低系统能耗.
问题阐述为:利用CRMS调度混合关键偶发任务集Γ={τ1,τ2,…,τn},计算静态能耗感知速度S,动态地回收高关键层次偶发任务预留的空闲时间以及偶发任务到达时间不确定所产生的空闲时间,确定偶发任务最终的执行速度Sc来降低系统低模式的能耗且满足调度正确标准.
3.2 计算偶发任务空闲时间
混合关键偶发任务集的实时利用率根据算法1计算,当τi释放任务实例且τi∈M时,提高偶发任务集的利用率,且将其从集合M中移除(算法1的步①~④).M代表可延迟偶发任务集合,该集合的偶发任务其释放2个相邻任务实例的时间大于最小释放间隔,初始时M=Γ.τi在时刻ri+Ti没有释放任务实例且τi∉M,降低偶发任务集的利用率,且将τi加入到集合M(算法1的步⑤~⑧).需要注意的是高关键层次偶发任务τi有任务实例完成执行,回收其预留的空闲时间,所以其相应的利用率变为Ci(LO)/(S×Ti).
算法1.利用率更新.
① 事件1:τi释放任务实例且τi∈M;
② 如果τi是低关键层次任务,则
U=U+Ci(LO)/(S×Ti);
③ 如果τi是高关键层次任务且其在当前时间之前有任务实例完成执行,则U=U+Ci(LO)/(S×Ti),如果其在当前时间之前没有任务实例完成执行,则U=U+Ci(LO)/(S×Ti)+(Ci(HI)-Ci(LO))/Ti;
④ 将τi从集合M中移除;
⑤ 事件2:τi在时刻ri+Ti没有释放任务实例且τi∉M;
⑥ 如果τi是低关键层次任务,则
U=U-Ci(LO)/(S×Ti);
⑦ 如果τi是高关键层次任务且其在当前时间之前有任务实例完成执行,则U=U-Ci(LO)/(S×Ti),如果其在当前时间之前没有任务实例完成执行,则U=U-Ci(LO)/(S×Ti)-(Ci(HI)-Ci(LO))/Ti;
⑧ 将τi加入到集合M;
⑨ 事件3:处理器处于空闲状态,设置M=Γ,U=0;
⑩ 如果U<0,设置U=0.
3.3 固定优先级混合关键调度算法
本节将提出固定优先级混合关键调度(fixed priority mixed criticality schedule, FPMCS)算法,该算法不仅能够利用静态空闲时间和高关键层次任务预留时间,而且还可以利用偶发任务到达时间不确定产生的空闲时间来进一步降低能耗.FPMCS算法基于CRMS算法分配任务优先级以及调度任务.FPMCS主要由利用率更新(算法1)、任务调度(算法2)以及速度选择(算法3)构成.
算法2.任务调度.
① 计算速度S(式(10)),设置M=Γ,U=0,根据CRMS算法分配任务的优先级;
② 将就绪队列设置为空集,将所有没有释放的任务实例放在等待队列中,偶发任务释放实例之后将其放到就绪队列中;
③ 在就绪队列中,选择优先级最高的τj执行;
④ 利用算法1和算法3动态决定τj的执行速度Sc;
⑤ 如果高关键层次偶发任务τj的执行时间超过Cj(LO)/Sc,系统切换到高模式;
⑥ 如果τj完成执行,将其从就绪队列移动到延迟队列.
算法3.速度选择.
① 如果高关键层次偶发任务τi的第1个任务实例完成执行,则U=U-(Ci(HI)-Ci(LO))/Ti;
② 如果系统处于高模式,则Sc=Smax;
③ 如果系统处于低模式,则Sc=U×S/F(n);
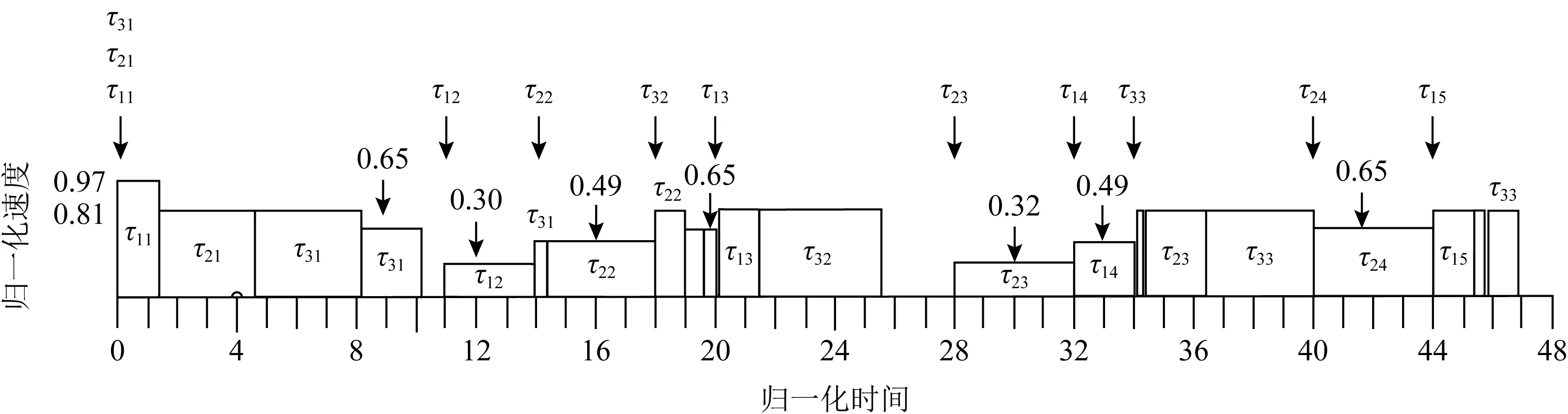
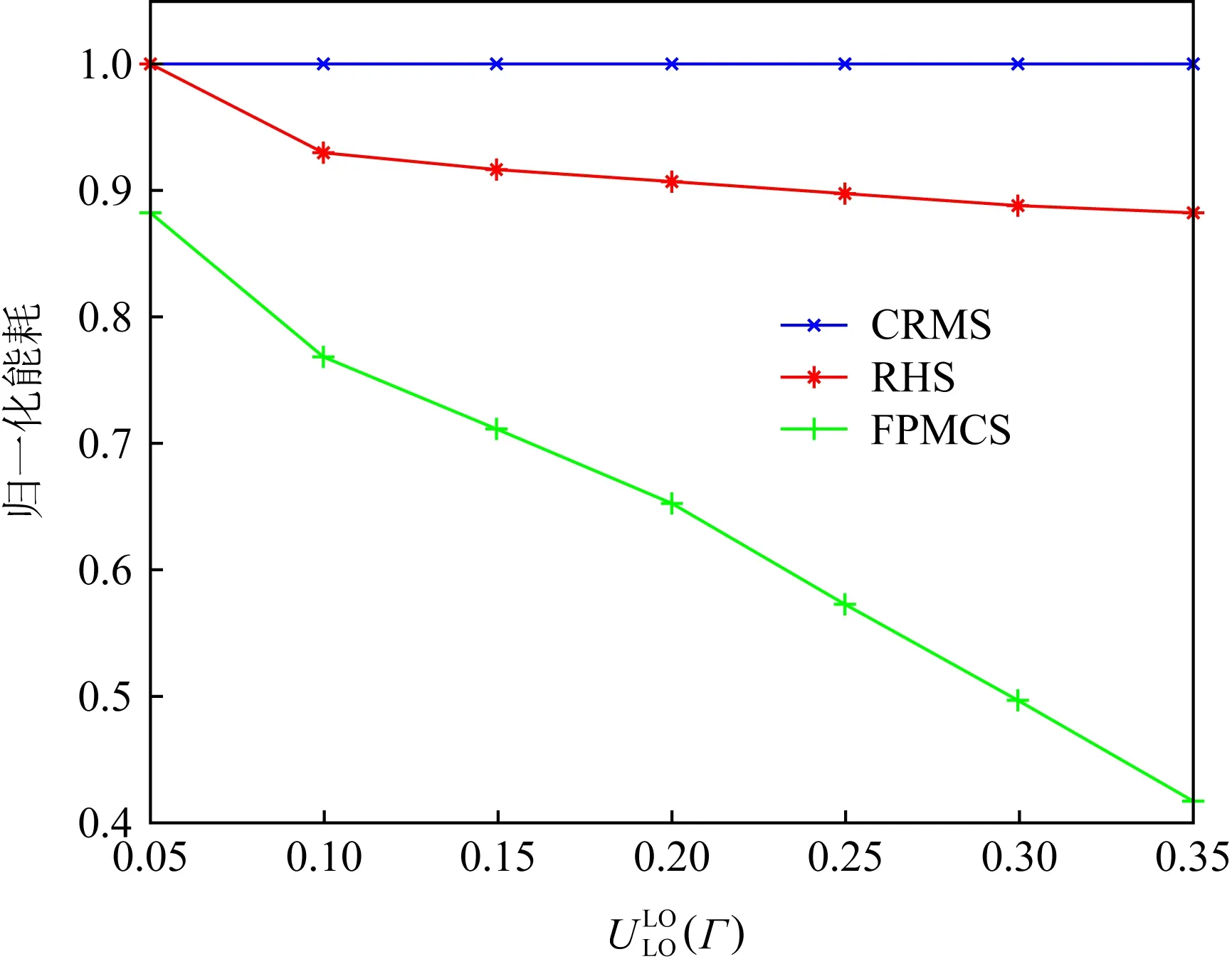
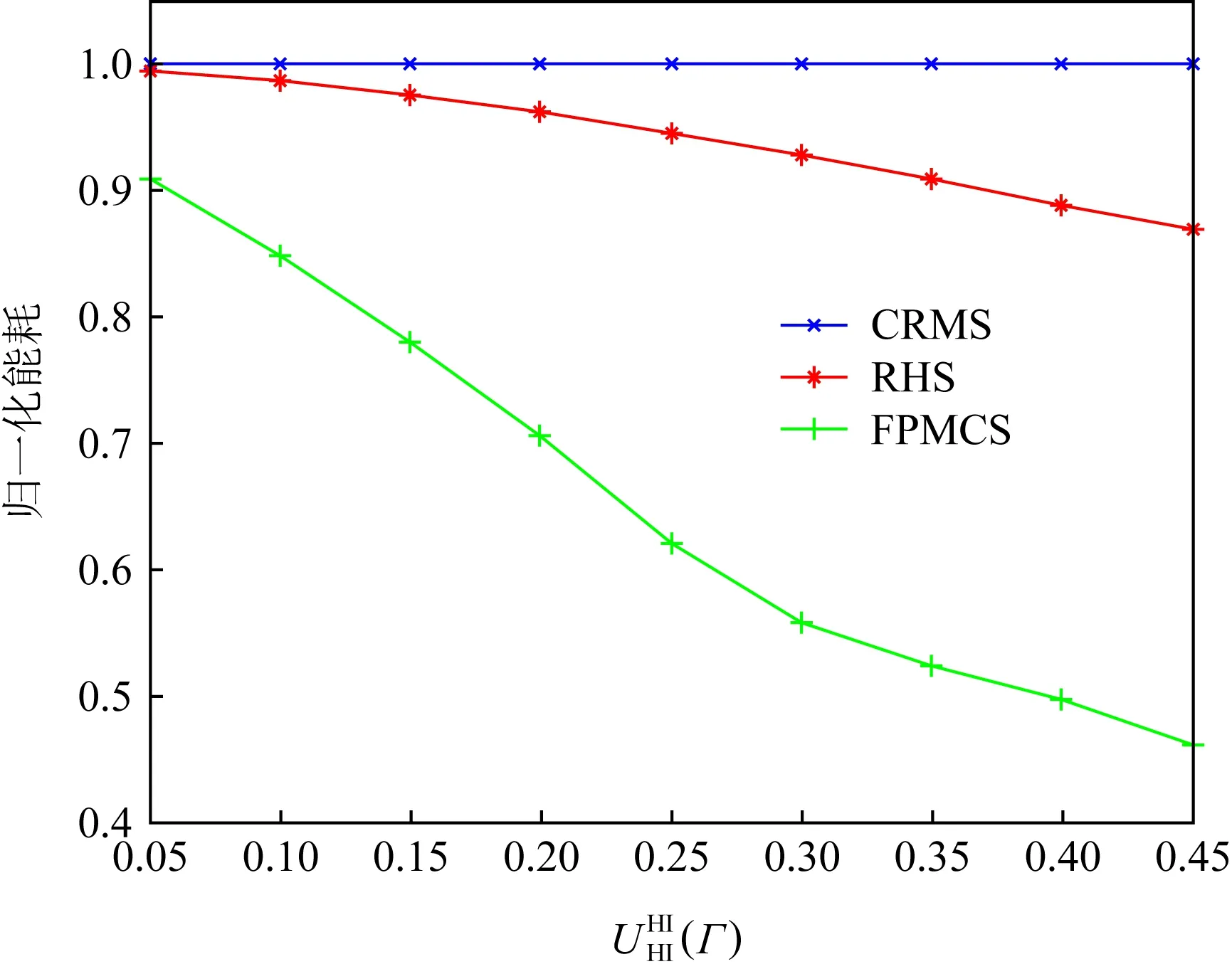
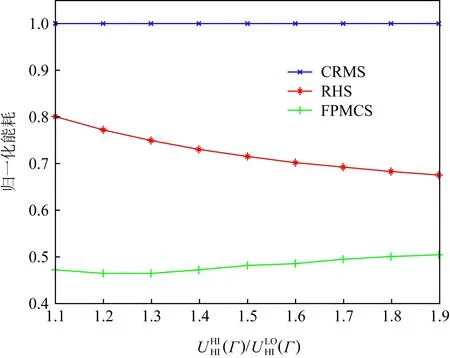
④ 如果Sc 需要注意的是,之所以Sc=U×S/F(n)是因为要确保系统的可调度性,计算出的速度必须满足CRMS调度可行的条件(算法3的步③). 算法1的时间复杂度为O(1),算法2的时间复杂度为O(n2),算法3的时间复杂度为O(1),因此FPMCS算法的时间复杂度为O(n2). 利用表1的混合关键偶发任务集Γ来解释FPMCS算法能够取得更好的节能效果.FPMCS算法在区间[0,48]调度混合关键偶发任务集Γ如图3所示: Fig. 3 FPMCS algorithm schedules mixed criticality sporadic tasks Γ in low mode图3 FPMCS算法在低模式调度混合关键偶发任务集Γ 图3中黑色箭头代表任务实例的到达时间,箭头上方的数字代表任务的执行速度.在时刻0,τ1以速度0.97开始执行且在时刻1.03完成执行.在时刻1.03,τ2以速度0.81开始执行且在时刻4.73完成执行.τ3在时刻4.73以速度0.81开始执行.在时刻8,τ1没有释放任务实例且其不属于集合M,降低偶发任务集利用率U;因此,τ3以速度0.65继续执行且在时刻10.08完成执行.在时刻11,τ1以速度0.30开始执行;在时刻14,τ2到达且其属于集合M,提高偶发任务集利用率U;因此,在时刻14,τ1以速度0.49继续执行且在时刻14.20完成执行.τ2在时刻14.20以速度0.49开始执行.在时刻18,τ3到达且其属于集合M,提高偶发任务集利用率U;因此,τ2以速度0.81继续执行.在时刻19,τ1没有释放任务实例且其不属于集合M,降低偶发任务集利用率U.τ2以速度0.65执行且在时刻19.51完成执行.在时刻19.51,τ3以速度0.65开始执行.在时刻20,τ1到达且其属于集合M,提高偶发任务集利用率U,此时,τ1抢占τ3,以速度0.81执行且在时刻21.23完成执行.在时刻21.23,τ3以速度0.81继续执行且在时刻25.77完成执行.剩余的偶发任务以相似的方法调度,不再赘述. FPMCS算法利用CRMS算法分配任务优先级以及调度任务.如果混合关键偶发任务集Γ的利用率不超过F(n),则CRMS算法调度混合关键偶发任务集Γ是可行的.因此,只需证明FPMCS算法以速度SC执行,混合关键偶发任务集Γ的利用率不超过F(n).定理3将证明FPMCS算法是可行的. 定理3.混合关键偶发任务集Γ的利用率不超过F(n),FPMCS算法以速度Sc调度混合关键偶发任务集Γ是可行的. 证明.只需证明FPMCS算法在超周期内调度混合关键偶发任务集Γ是可行的.令βspeed={β1,β2,…,βm}为所有速度变化区间的集合,其中区间βi开始时刻是在上一个空闲区间的结束和其结束时刻是在下一个空闲区间的开始.因此,βspeed的长度正好等于混合关键偶发任务集Γ的超周期.令Sspeed={S1,S2,…,Sm}为与区间βspeed的相对应处理器速度集合.令auti={a1,a2,…,am}为βspeed的相对应M的利用率集合.令Ui为βi以速度S执行的利用率,Ui计算为 (11) 在区间βi开始之前,延迟到达任务集合M包括所有释放任务实例时间超过其最小时间释放的任务,因此βi的相应利用率ai计算为 (12) Ui=F(n). (13) 区间集合βspeed的利用率Uβspeed等于子区间与全部区间的比值乘以该子区间的利用率之和,即: (14) Uβspeed=F(n). (15) 证毕. 利用C语言实现混合关键偶发任务的调度仿真器来评价所提出算法的性能.该调度仿真器基于固定优先级调度策略.仿真实验中比较3种算法:1)CRMS算法,在低模式所有任务以速度S执行;2)RHS算法,该算法基于CRMS,在低模式能够利用高关键层次任务预留的空闲时间[17]降低能耗;3)FPMCS算法,该算法不仅能够利用静态空闲时间和高关键层次任务预留时间,而且还可以利用偶发任务到达时间不确定产生的空闲时间来进一步降低能耗. Fig. 4 Effect of on energy consumption of algorithms图对算法能耗的影响 Fig. 5 Effect of on energy consumption of algorithms图对算法能耗的影响 consumption of algorithms图比值对算法能耗的影响 固定优先级混合关键系统偶发任务能耗感知调度是解决系统实时性与低能耗的关键,而偶发任务到达时间不确定是调度过程中面临的一大难题,所提出的FPMCS算法通过事件触发的方法实时更新混合关键偶发任务集的利用率,通过该利用率实时计算任务的执行速度,达到充分利用偶发任务到达时间不确定产生的空闲时间降低能耗的目的.此外,FPMCS算法还可以利用高关键层次任务预留的时间来降低能耗.最后,通过理论分析和仿真实验验证了FPMCS算法的可行性且具有良好的节能效果.仿真实验表明:FPMCS算法比现有的RHS算法节约大约33.21%的能耗. 作者贡献声明:张忆文负责文章的设计与实现;高振国协助完成实验数字分析;林铭炜协助数据的整理.3.4 算法实例
3.5 可行性分析

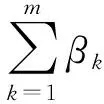
4 仿真实验
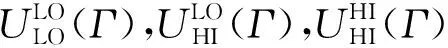
5 结 论

