逐级特征降维与智能寻优的辛烷值预测模型*
聊城大学数学科学学院 孙梦迪 孙忠贵
在催化裂化汽油精制过程中,降低硫含量保持辛烷值,对提高汽油的动力经济性有着重要意义。但这一过程中涉及的操作变量较多,难以调控。本文借助相关性分析,稀疏PCA和神经网络对操作变量进行逐级降维,建立辛烷值损失预测模型,并采用遗传算法进行决策寻优。训练数据集上调控与预测结果充分表明了所建模型的合理性。
由汽油燃烧产生的汽车尾气严重污染了大气环境,这对汽油清洁化提出了越来越高的要求。汽油清洁化的重点是在尽最大可能保持汽油中辛烷值的基础上降低其硫、烯烃含量[1]。由于含硫和高硫原油占绝大多数,为满足汽油质量标准必须对其催化裂化获得的汽油进行精制处理。辛烷值是表示汽车发动机燃料(汽油)的抗爆性能好坏的一项重要指标。汽油的辛烷值越高,抗爆性就越好,发动机就可以用更高的压缩比。现有技术在炼油工艺过程一个主要目标就是保持汽油的辛烷值达标,因此建立汽油辛烷值损失预测模型非常重要的[2-4]。本文针对某石化企业催化裂化汽油精制脱硫装置4年的历史数据。通过对367个变量进行降维处理,筛选出建模的主要变量,来建立汽油辛烷值损失模型,进一步优化主要变量的操作策略。
1 模型建立
1.1 数据处理
在原始数据中,大部分变量数据正常,但由于装置本身限制或数据采集不准确等客观原因,导致部分变量均存在问题:部分变量只含有部分时间段的数据,部分变量的数据全部为空值或部分数据为空值。因此,我们需要对原始数据进行预处理。步骤如下:
(1)删除数据中全部为空值或空值过多无法补充的操作变量,对于只有部分空缺数据的位点,用此位点前后2h内的平均值填充;
(2)删除325个样本数据全部为空值的变量,求出各操作变量的取值范围,采用最大最小的限幅方法剔除数据不在此范围内的相应操作变量所对应的样本;
(3)利用3σ准则[5]去除操作变量里含有较大误差的异常值,设被测变量为x1,x2,…,xn,我们需要根据
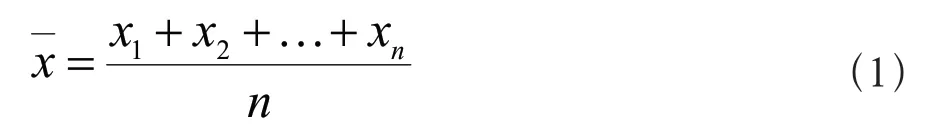
算出算术平均值,根据

算出剩余误差,根据贝塞尔公式
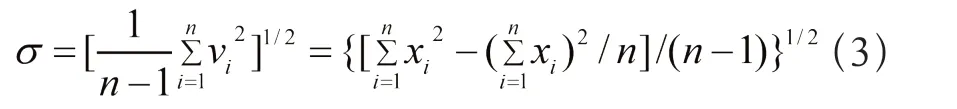
算出标准误差σ;
(4)最后对285号和313号这两个样本前后2h内的数据取平均值,得到与辛烷值测量时间相对应的各个操作变量的数据,其中285号样本数据可用,而313号样本数据未能通过检,故只将285号样本数据加入到原始数据,取代相应数据。
1.2 寻找建模主要变量
由于炼油工艺过程复杂,可调整的操作变量(控制变量)具有高度非线性和相互强耦联性,建立辛烷值(RON)损失预测模型涉及13个非操作变量和354个操作变量(共计367个变量),本文筛选出具有代表性和独立性的30个以下主要变量来建立辛烷值损失预测模型。由于非操作变量属于固有属性,对汽油辛烷值的影响极其重要,我们仅需对可操作变量进行处理。我们的降维方法总结为逐步递进的三个步骤:
(1)利用相关性分析[6]去除高度线性相关的操作变量;(2)利用稀疏PCA[7-9]降维筛选出重要程度较大的操作变量;(3)利用神经网络[10]去除非线性强相关的变量。相应流程如图1所示:
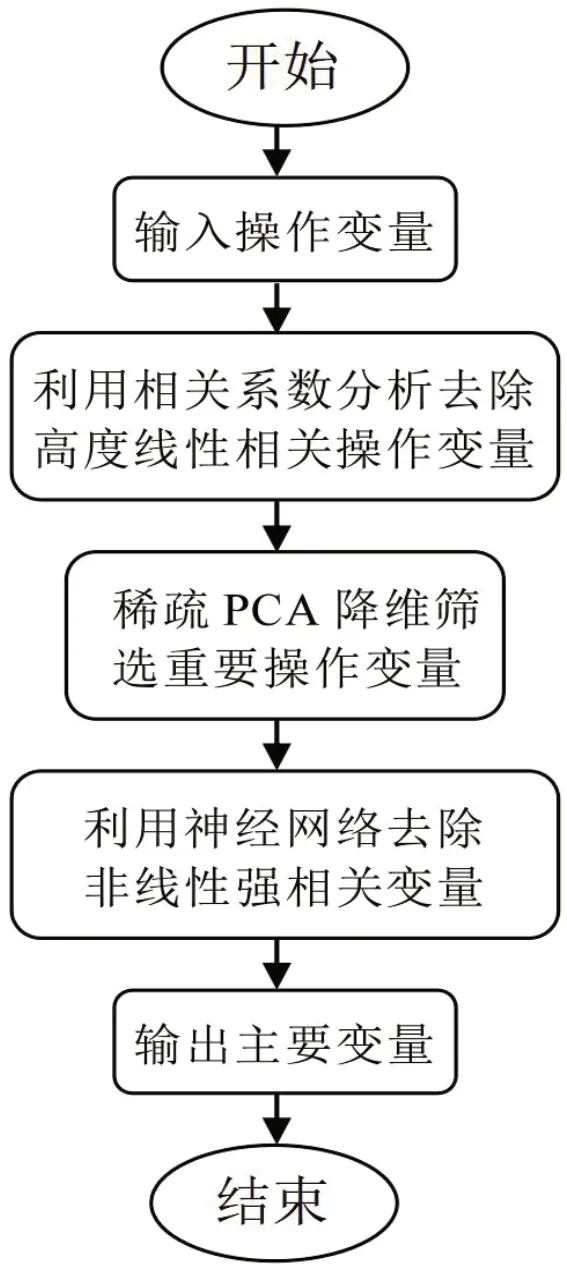
图1 逐步降维流程图Fig.1 Stepwise dimension reduction flowchart
1.2.1 相关性分析去除高度线性相关操作变量
首先根据各操作变量之间的相关系数,选出相关系数较大,即具有明显线性相关的操作变量进行聚类,并用与聚类中心最近的个体代表所有类成员,对具有高度线性相关的操作变量进行剔除,从而实现第一步降维。
首先根据
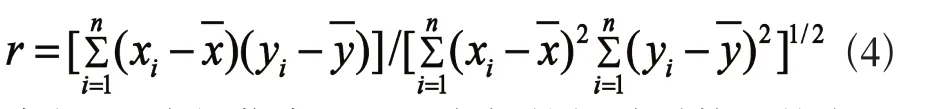
求得354个操作变量两两之间的相关系数,其中x,y表示两个不同操作变量,xi或yi代表同一操作变量不同样本的测量值,相关系数矩阵的图像表示如图2所示。
由图2可知,大量相关性系数较高,这表明原操作变量之间存在较强的线性关系。我们以0.90为相应阈值进行聚类,筛选出相关系数在0.90~1.00之间的类别,并用与类中心最近的个体代表所有类成员,从而去除具有高度线性相关的操作变量。将操作变量总数由354降至207。
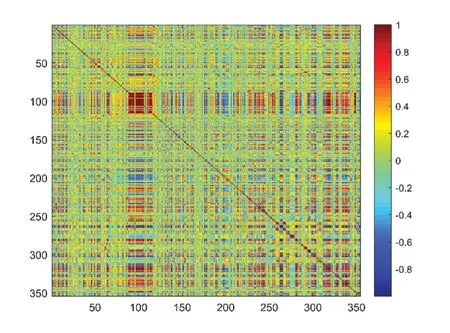
图2 相关系数矩阵图像表示Fig. 2 Image representation of correlation coefficient matrix
1.2.2 稀疏PCA降维筛选重要操作变量
需注意的是,通过第一步降维(第1.2.1节),尽管我们去除了大量高度线性相关的操作变量,剩余变量在数据表示上往往具有不同的重要程度。稀疏主成分分析(SPCA)通过增加主成分载荷中零元素个数,使得主成分可以用最少且最有代表性的变量的线性组合来表示。本文借鉴文献[11]的硬阈值法,首先对原始数据进行PCA降维操作,然后将主成分载荷中绝对值小于给定阈值的元素截断为0,达到剔除非重要操作变量的目的。步骤如下:
(1)设原始p个操作变量x=(x1,x2,…,xp)T的n次观测数据为xi=(xi1,xi2,…,xip)T,i=1,2,…,n,样本数据矩阵为:
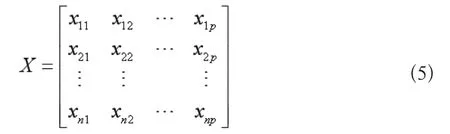
对样本数据矩阵进行如下标准化变换:
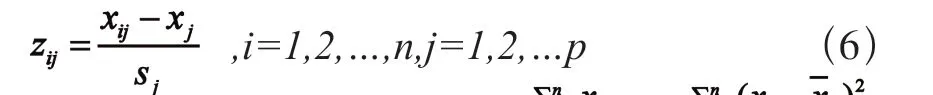
(2)对标准化矩阵Z求相关系数矩阵R,R=(rij)p×p,其中,
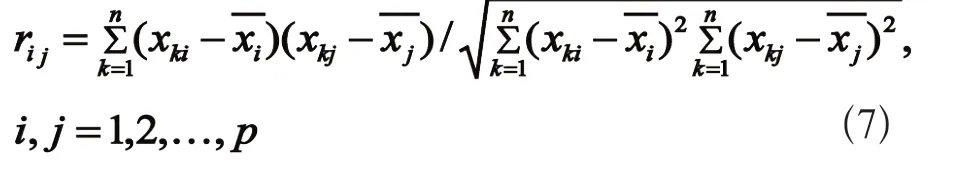
(3)求解相关系数矩阵R的特征方程det(R-λE)=0,得到p个特征根λ1,λ2,…,λp,
(5)计算m个主成分相应的单位特征向量:
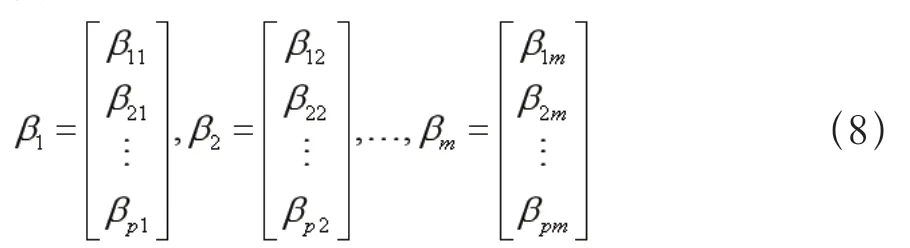
(6)计算主成分:

(7)稀疏主成分:
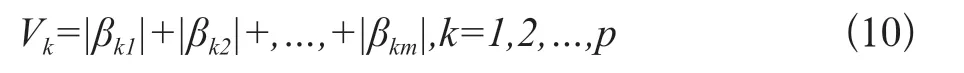
对Vk求期望和方差δk,将小于βk<ε的主成分载荷置零,即将相应操作变量xk剔除。在具体实现时,根据拉依达准则,我们取通过此步降维,我们进一步将操作变量由上一步的207个降至172。
1.2.3 神经网络去除非线性强相关变量
通过前两步降维(第1.2.1和1.2.2节),尽管可操作变量已经由354降至172,其与降至30个以下的目标依然相差甚远。我们注意到,无论是第一步所用的相关系数处理还是第二步用的稀疏PCA操作,都属线性分析范畴。而这众多变量之间还存在大量非线性关系,神经网络则是刻画非线性关系的强有力工具[12]。
如图3所示,为去除非线性强相关的变量,本文采用一个3层神经网络,隐藏层的神经单元数量均设置为3。其基本动机是:一个变量能被其他变量所表示,将意味着其不具备很好的独立性,从而被剔除,达到特征降维的目的。具体实现时,选择样本数据的80%作为训练集,20%作为测试集。输出变量xk若能被其他变量(非操作变量与剩余操作变量)通过神经网络进行较好的表示(相对误差小于阈值0.80),则将其剔除,否则保留。经过此步操作,主要变量降至17维,其中操作变量6维。
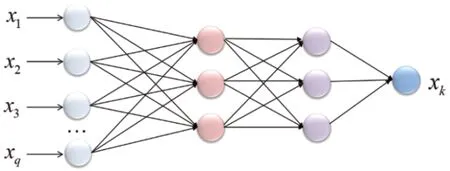
图3 用于去除非线性强相关变量的网络结构Fig.3 Network architecture for removing nonlinear strongly correlated variables
1.3 建立辛烷值(RON)损失预测模型
考虑到炼油工艺的复杂性,本文采用相对复杂的神经网络学习辛烷值预测模型。如图4所示,其中4个隐藏层的结点数量均为13,输入变量为降维后的17个特征,输出变量为辛烷值和硫含量。依然选取样本数据的80%作为训练集,20%作为测试集。训练出各主要操作变量与辛烷值和硫含量的模型。
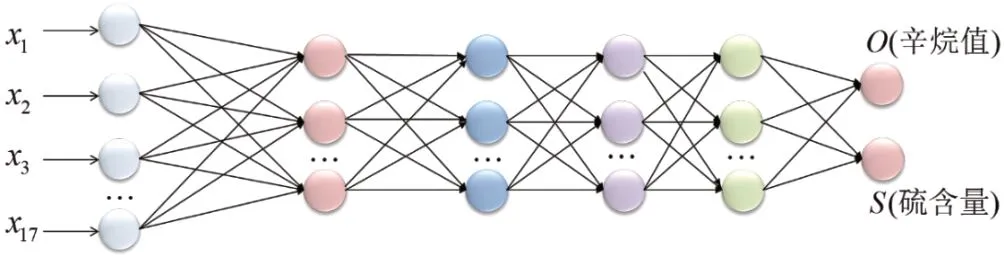
图4 用于辛烷值损失预测的网络结构Fig. 4 Network architecture for octane loss prediction
1.4 主要变量操作方案的优化
在调整优化过程中,由于变量过多,使用传统的迭代优化算法容易陷入局部极小值的陷阱而出现“死循环”的现象[13],使得迭代算法无法进行。而遗传算法[14]全局优化算法具有良好的全局搜索能力,可以快速地将解空间中的全体解搜索出,而不会陷入局部最优解的快速下降陷阱;并且利用它的内在并行性,可以方便地进行分布式计算,加快求解速度。
遗传算法的主要步骤如下:
(1)采用上一步的神经网络,在搜索空间U上定义一个适应度函数f(x),在硫含量不大于5μg/g,辛烷值越大和硫含量越小,适应度越强,给定种群规模N=30,变异率Pm=70%,代数T=50;
(2)我们将样本数据设为初始个体,并在其附近产生N-1个个体s1,s2,…sN-1,组成初始种群S={s1,s2,…sN-1},置代数计数器为t=1;
(3)交叉变异;
(4)依据适应度函数产生新的种群;
(5)t=t+1,若t (6)算法结束。 辛烷值和硫含量在测试集上表现如图5所示。其中辛烷值的预测表现较好,而对硫含量的预测也基本稳定。这表明,在变量维数由367降为17后,通过神经网络训练,依然能够对上述两个化工指标能较好地表示。这为后续操作方案的进一步优化奠定了基础。 图5 辛烷值和硫含量在测试集上的预测效果Fig. 5 Predictive results of octane value and sulfur content on test sets 对于具体133号样本,同样采用上述方案,在硫含量满足不大于5的前提下,得到辛烷值的预测值为88.50,辛烷值损失降幅大于30%。具体调整方案为:汽油产品去气分流量(833.98)、闭锁料斗氧含量(5)、补充氢压缩机出口返回管流量(0)、紧急氢气去R-101流量(39.38)、循环氢至闭锁料斗料腿流量(0.86)、D121顶去放火炬流量(283.16)。 优点: 逐步降维:根据变量关系的不同类型,采用逐步递进的降维方式,有效克服了维数灾难; 用神经网络刻画复杂的非线性关系:浅层网络刻画操作变量关系,深层网络刻画化工过程,符合实际; 智能寻优:用遗传算法进行操作方案的优化,加速调控过程。 缺点: 没有考虑不同方案的调控成本; 建模过程中的随机性因素可能会导致调控过程的稳定性不够; 数据整定策略可进一步改进。 本文对操作变量的重要性是通过经典PCA中相应系数的大小顺序来刻画的,考虑到各变量之间关系的复杂性,将其映射到高维空间,采用核PCA或许能够对这种关系进行更为合理的描述[15-18]。此外,本文建模主要依赖数据驱动,缺少机理分析。面对实际问题,将机理分析与数据驱动相结合往往更有助于调控决策。 本文首先依次借助相关性聚类分析,稀疏PCA和神经网络对操作变量进行逐级降维;其次,采用神经网络对辛烷值损失建立预测模型;最后,利用遗传算法进行调控决策寻优。基于上述模型所获得的调控策略,训练数据集上的预测结果充分表明了所建模型的合理性。 引用 [1] 龙梦舒,闵超,赵伟,等.基于机器学习的汽油加氢裂化辛烷值损失预测和脱硫优化[J].科学技术与工程,2022,22(3):1076-1084. [2] 陈亚丽,苟苗苗,邵露娟,等.基于RF-XGBoost算法的汽油辛烷值损失预测模型[J]. 炼油技术与工程,2021,51(12):49-53. [3] 楚庆玲,平振东,于明加,等.基于RBF神经网络的辛烷值损失预测模型[J].物联网技术,2021,11(11):104-107. [4] 赵林,李希,谢永芳,等.基于自适应变量加权的汽油辛烷值预测方法[J/OL].控制与决策:1-7[2022-02-01]. [5] Friedrich Pukelsheim.The Three Sigma Rule[J].The American Statistician,1994,48(2):88-91. [6] 李云燕.仿真数据相关性分析方法研究[D].哈尔滨:哈尔滨工业大学,2011. [7] 黎明.稀疏主成分分析算法研究与应用[D].合肥:中国科学技术大学,2021. [8] 杨欣.稀疏主成分分析的两阶段法[J].应用数学进展,2017,6(9):1174-1181. [9] CADIMA J,JOLLIFE I T.Loading and Correlations in the Interpretation of Principal Components[J].Journal of Applied Statistics,1995(22):203-214. [10] Aston Zhang,Mu Li,Zachary CLipton,et al.动手学深度学习[M].北京:人民邮电出版社,2019. [11] 张良均,杨坦,肖刚,等.MATLAB数据分析与挖掘实战[M].北京:机械工业出版社,2015. [12] 司守奎, 孙兆亮.数学建模算法与应用[M].北京:国防工业出版社,2015. [13] 张会芳.凸优化问题最小范数解的迭代算法及应用研究[D].天津:中国民航大学,2018. [14] 杨超.基于多目标优化的反馈多智能体遗传算法研究[D].天津:天津职业技术师范大学,2021. [15] 孙永科,周开来.核PCA神经网络集成算法在文本识别中的应用[J].科技通报,2013,29(8):124-126. [16] 李庆震,祝小平.基于核PCA的智能图像分析算法[J].弹箭与制导学报,2007(5):189-192. [17] 张国云,彭仕玉.核PCA支持向量机算法研究[J].湖南理工学院学报(自然科学版),2006(4):23-26. [18] 周志华.机器学习[M].北京:清华大学出版社,2016.2 模型求解
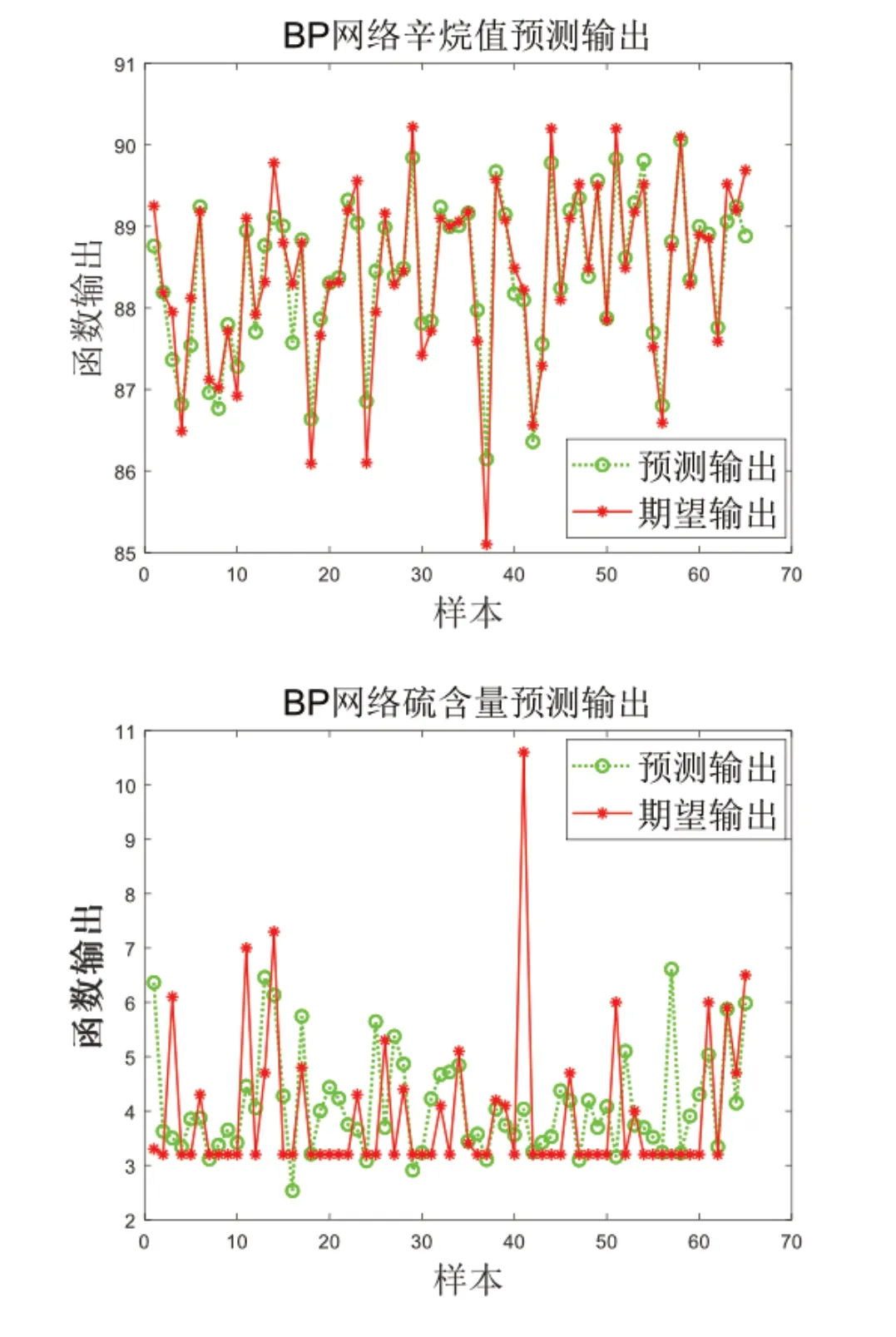
3 模型的评价与讨论
3.1 模型优缺点
3.2 模型的进一步讨论
4 结论

