合情推理在小学数学教学中的应用

刘瑞容

摘要：“合情推理”是小学数学教学的重要组成部分。在数学教学中，教师要构筑合情推理空间，鼓励学生大胆猜想，经历合情推理思辨、求证的过程并感悟合情推理的或然性。在合情推理过程中，教师要引导学生主动观察、实验、实践，让学生形成合情推理技能，感悟合情推理思想，提升学生合情推理能力，促进学生数学素养的提升。

关键词：小学数学;合情推理;或然性

美国数学教育家波利亚曾经这样说：“数学既要教证明，又要教猜想。”学生的数学学习，不仅仅依靠严密的数学推理，还依靠富有预见性、合情性的推理。课标2011年版指出：“合情推理是从已有的事实出发，凭借经验和直觉，通过归纳和类比等推断某些结果。”不完全归纳推理和类比推理统称“合情推理”，又叫做“或然推理”“似真推理”。

合情推理能力不是与生俱来的，它具有一个发展过程，需要从小培养。儿童获得数学知识的过程其本质就是从合情推理提升为演绎推理的过程。由于儿童的思维发展水平和层次，决定了其创造性思维发展的第一关键期就在小学阶段。小学教材中有很多合情推理的素材，小学中的很多知识也都与现实生活联系紧密，给学生们提供了丰富的合情推理素材，小学是培养学生的合情推理能力的重要阶段。

一、构筑思维空间，激发学生合情推理需求

东北师范大学史宁中教授认为，数学的基本思想有抽象、推理与模型。推理是儿童在数学学习中内隐性思维的主要形式，它分为直觉性的合情推理和逻辑性的演绎推理。其中，合情推理是儿童推理的主要形式。一定的情境、一定的形式内容等均是合情推理的助推剂。在数学教学中，教师要创设合情推理的需求、机会，选择一些典型的、可以进行合情推理的素材，从而营建一定的合情推理思维时空。

例如，在教学人教版六年级上册的《比的基本性质》一课时，教师先带领学生回顾旧知：分别是三年级学过的商不变的规律，四年级学过的小数的性质，五年级学过的分数的基本性质;然后让孩子们比较除法、小数、分数、比之间的联系与区别;其次让孩子们交流在除法、小数、分数、比中有哪些规律和性质？有了这些情境创设和知识准备（包括形式关联、内容关联等），学生猜想类推出在“比”中也应该有类似的性质，并作出学生自己的表述，水到渠成;最后放手让学生验证，他们有的举例验证，有的化成除法、分数后验证等等。整个过程孩子们是一个发现者、探索者，在自主中获得数学概念、方法、定律和公式。

在本次教学活动中，教师带领学生找寻已知和未知之间“衔接点”，构筑合情推理的思维空间，激起学生合情推理的需求，引导学生合情推理的方向，赋予学生合情推理的感性思维力量。

二、加强思辨猜想，培养学生合情推理能力

俗话说“童言无忌”。一方面天生敢想、敢说，喜欢问问题，这是有利于数学猜想的心理优势;另一方面，儿童思维的抽象性、逻辑性处在逐步发展的过程中，有时也会随心所欲，脱离数学事实提出想法。因此，教师应当引导学生以事实、经验为基础，由个别到一般或由此及彼，发现问题、提出问题，大胆“假设”。

例如，在教学《圆锥体积公式》时，为什么“圆锥体积等于等底等高圆柱体积的三分之一”？受小学数学知识的局限，教材与教学都只用实验事实说话（如上图），使學生“知其然”，不再作其他任何“所以然”的解释。有必要反思，教学时直接给出等底等高的圆锥和圆柱容器，学生只是机械地倒水或沙子，结果正好倒三次。这样的“发现”，合情推理的成分实在微不足道。能否改进呢？尝试如下：

师：我们已经学会了计算哪些物体的体积？

生：长方体、正方体、圆柱。

师：它们统一的体积公式是什么？

生：底面积乘高。

师：我们今天要探究圆锥的体积公式，你有什么猜想？请没有预习、不知道公式的同学说。

生：我想，圆锥的体积也和它的底面积、高有关。

师：为什么呢？

生：因为圆锥的底面积越大，体积越大：高越大，体积也越大。

师：有道理的一个猜想。再回想一下，图柱体积公式是怎样推导的？

生：用割补的方法转化为长方体得来的。

师：转化前后的圆柱体与长方体有什么关系？

生：它们等底等高。

师：那么，为了求圆锥的体积，你想让它转化成什么体？用割补的方法，还是用其他的方法进行实验？

生：转化为圆柱体，用倒水或倒沙子的方法做实验。（也有学生提议转化为长方体）

师：对用来装水或沙子的圆锥、圆柱体或长方体容器的大小，你有什么想法？

生：应该等底等高。

在此基础上，教师给出等底等高的圆锥、圆柱和长方体（圆锥、圆柱的底面半径为5厘米，长方体底面是正方形，边长为8.9厘米），让学生自己选择实验容器。

实践表明，加强合情推理的环节，是可行的、有效的。有了这些思辨与猜想，增加了容器的选择，倒水、倒沙子的实验就不再盲目、单一。

三、经历归纳陷阱，生成合情推理素养

弗赖登塔尔深刻地指出：“将数学作为一种活动来进行解释和分析，建立这一基础之上的教学方法，我称之为再创造方法。”合情推理也必须引导学生经历再创造，这是数学教学的最基本的原则。引导学生经历合情推理过程，既可以让学生进行不完全归纳，也可以让学生进行类比。所谓“不完全归纳”，就是从“特殊”到“一般”的整体;所谓“类比”，就是从“特殊”到“特殊”的推理。归纳，既可以依据形式归纳，也可以依据内容归纳。同样，类比既可以依据形式进行类比，也可以依据内容进行类比，还可以依据方法进行类比。

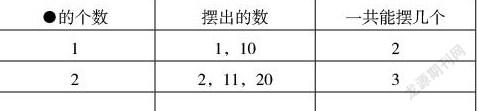
例如，在教学低年级综合与实践活动“摆一摆，想一想”时（如图），学和依次用1个●、2个●......摆一摆，填一填。当填到3个●、4个●时，就有学生认为规律已经显现，不用再摆了。

让学生回答：用8个●一共能摆几个数？9个●呢？多数学生会毫不犹豫地递推：8+1，9+1。至此，归纳推理的结果都是对的。如果再进一步追问：用10个●摆摆看，有人发现不对了：10个●都用上，是不能摆一位数的，也无法摆出个位是0的两位数。为什么呢？因为数字最到9，所以10个不能都摆在一个数位上。

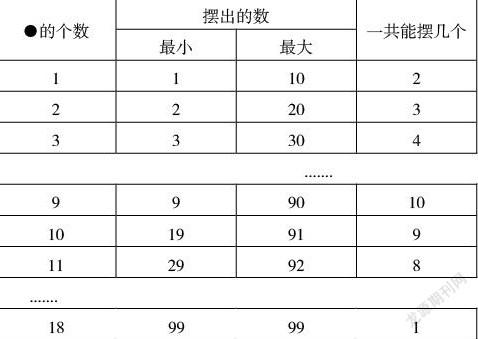
对于学有余力的学生，还可以引导他们自己跳出陷阱。比如，给出下表，先让学生按已发现的规律填写1至9这几行。然后引导他们继续操作、思考，完成10至18这几行。理解能力强的学生能够想明白，为什么这个活动最多到18个？因为最大的两位数是99。

这一探究性活动能让低年级学生感受到数学好玩，并使一些学生惊叹数学规律的奇妙：原来数学规律会变，要小心上當。在合情推理得到结果之后，教师一定要引导学生反思：是什么引发了自己做出这样的推理？是不是考虑了所有的要素？还可以进行怎样的推理？……通过反思，学生可以由此及彼、由表及里、去伪存真，从而探寻到本质性的东西。

四、制造类比冲突，感悟合情推理或然性

怎样正确引导感悟合情推理的或然性既然“合情推理”又叫做“或然推理”、“似真推理”，便意味着经常呈现看似合情合理的正确现象，实际结果却可能是错的。教学时不要急于朝正确方向引导， 而要设置“陷阱”，让学生通过“折腾”，自己发现合情推理可能出错。

例如，教学《3的倍数特征》时，可以先复习2、5的倍数的特征，小结：判断一个数是不是2、5的倍数，只要看个位。然后提问：“能否由2、5的倍数的特征类推3的倍数的特征？为什么？”由于前面学习时已经连续两次通过观察个位数找到特征，所以探究3的倍数特征时，学生会很自然地继续寻找个位数的特征。只要让学生依次写出前10个3的倍数3、6、9、12......30，或者让他们在百数表上依次圈出3的倍数，学生就都能发现，类比无效。因为3的倍数个位上从0到9都有可能。也就是说，判断一个数是不是3的倍数，不能只看个位。

实践证明，让学生经历多次猜想、验证的探究过程，即类比猜想→举例推翻猜想→改变方法→再次猜想→验证猜想→……这种教学表面上看比较费时，不能够顺利地得出结论，但主要目的是造成认知冲突，让学生获得类比可能无效的体验，从而促使学生自己排队只看个位的思维定势，进而变换观察角度，深入展开探究活动，去发现新的规律，使学生获得更多的数学活动经验，感悟合情推理的或然性。

总之，在数学教学中，教师要创设合情推理的需求、机会，选择一些典型的、可以进行合情推理的素材，从而营建一定的合情推理思维时空，调动学生主动参与合情推理的积极性，发挥出学生在数学课堂合情推理中的主体作用，给学生创造发现问题、假设问题、提出问题、猜想问题、分析以及推理解决问题的环境条件，潜移默化地将合情推理意识牢牢树立在学生心中，让合情推理助力数学课堂。

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准（ 2011年版）[M]..北京： 北京师范大学出版社，2012.

[2]秦玮远，何向东.合情推理的逻辑——从欧拉猜想说起[J].安徽大学学报，2007（9）.

[3]史宁中，柳海民.素质教育的根本目的与实施路径[J].教育研究，2007（ 8） ： 12.

[4]曹培英.小学数学合情推理的教学研究[J].小学数学教师，2015（7-8）.

[5]杨慧娟，杜鹏.新课标下重析波利亚的合情推理思想[J].数学通报，2006，（02）.

[6]陈水平，合情推理在数学学习建构中的作用[J]..数学教育学报， 1998， 7 （3）.

[7]韩富万，李善明.合情推理的地位与功能[J].北京教育学院学报，2000， 14（2）.

[8]连四清，方运加.“合情推理”辨析[J].课程·教材·教法，2012（5） ： 54.

[9]徐谦.核心素养背景下小学数学合情推理能力的培养[J].成功：中下，2017（15）