A*算法在移动机器人路径规划中的研究

鲁 毅，高永平，龙江腾

(东华理工大学 信息工程学院，江西 南昌 330013)

0 引言

随着工业化社会的发展，货物的搬运和输送成为重要的问题，其中移动机器人技术得到了极大的关注[1]，移动机器人技术可以极大地提高货物的运输能力，使得货物的运输更加的自动化，而在移动机器人技术中，机器人路径规划算法[2]一直是研究重点，路径规划算法有Dijkstra算法[3]，BFS算法[4]，A*算法[5]等，Dijkstra算法可以搜索到一条最优路径，但是搜索效率太低，BFS算法搜索效率很高，但是不一定能搜索到一条最优路径，A*算法结合了Dijkstra算法和BFS算法的优点[6]，但是也存在一些缺点，因此，本文提出改进A*算法，既能寻找到一条最优路径，而且搜索效率也比较高。

1 传统寻路算法

1.1 Dijkstra算法

Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法[7]，用于计算从起点到其他各顶点的最短距离。主要是从起点开始不断向外搜索，直到搜索到终点结束。算法原理：假设一个带权有向图G，将其分成A，B两个集合，其中A集合中存放的是已访问顶点和其最短路径值，B集合中存放的是未访问的顶点，算法步骤如下：

1)初始时，将起点S放在集合A中，集合B中存放其他所有顶点和起点S到其他顶点的距离。

2)从集合B中选取到起点S的最短距离的顶点a，并将顶点a加入到集合A中，同时从集合B中删除顶点a.

3)以顶点a为中间点，更新集合B中各个顶点到起点S的距离。

4)循环执行步骤2和3，直到遍历完图中所有的顶点为止。

Dijkstra算法是一种盲目式搜索算法，所以搜索效率较低，对于n个节点的图，计算起点到其他各节点的最短距离，算法的时间复杂度为O(n2)，因此，在大型地图中寻路效率比较低。算法流程图如图1所示。

图1 Dijkstra算法基本流程

1.2 最佳优先搜索算法

最佳优先搜索算法是一种启发式搜索算法[8]，是在广度优先算法的基础上形成的，该算法使用了估价函数，利用估价函数计算当前节点到目标节点的估价值，然后选择估价值最小的节点进行访问，直到搜索到目标节点为止。最佳优先搜索算法(BFS)不能保证找到的路径是一条最短路径，但是其计算过程相对于Dijkstra算法会快很多。

算法实现需要两个列表，A列表和B列表，A列表中是将要被访问的节点，B列表中是已被访问的节点，算法步骤如下：

1)初始时，将起点放入到A列表中，B列表为空；

2)从A列表中选取估价值最小的节点k,并对k的所有子节点m进行如下操作：

如果m子节点不在A列表和B列表中时，将m子节点加入到A列表中，并计算出m的估价值，并对A列表中的节点依据估价值进行排序。

如果m节点在A列表中，重新计算m节点的估价值，并将该估价值和A列表中m的估价值进行比较，如果小于A列表中的估价值，则将A列表中的估价值进行替换，并且对A列表重新排序。

如果m在B列表中，重新计算m节点的估价值，并将其和B列表中m节点的估价值进行比较，如果小于B列表中m的估价值，则将m从B列表中删除，并加入到A列表中，然后对A列表中的节点进行排序。

3)将节点k从A列表中删除，并加入到B列表中。

4)循环执行上述步骤，直到搜索到目标节点或者A列表为空为止。

最佳优先搜索算法在搜索路径的过程中效率极高，但是最佳优先搜索算法只考虑了当前点到目标点的估计值，没有考虑起点到当前点的成本值，因此不一定能够搜索到一条最优路径。

2 传统A*算法

A*(A-Star)算法是一种效率高且能搜索到最优路径的算法[9]。有许多的寻路算法都是在A*算法的基础上形成的,例如D*算法[10]和NavMesh导航算法[11]，该算法利用了启发函数的特性，使用启发函数计算出当前点的估价值，利用估价值来选取最优节点，最终搜索出一条最优路径。

A*算法结合了Dijkstra算法和最佳优先搜索算法的优势[12]，它在一定程度上保留了Dijkstra 算法搜索最短路径的能力，又引入了最佳优先搜索算法的贪婪策略，防止了算法盲目的搜索，组合成了一个融合性的评价函数，评价函数为：

F(n)=G(n)+H(n)

(1)

式(1)中，n为当前节点，F(n)是从起始节点到目标节点的估计值，G(n)是起始节点到当前节点的实际值，H(n)是当前节点到目标节点的估计值，也称为启发函数，启发函数的计算有多种，如曼哈顿距离、欧几里得距离、对角线距离等。本文启发函数采用曼哈顿距离[13]，即为：

H(n)=|x1-x2|+|y1-y2|

(2)

式(2)中，(x1,x2)是当前节点的坐标，(y1,y2)是目标节点的坐标。

A*算法就是利用估价函数来对每一个节点进行评估，得到估价最优的节点，再从这个节点继续搜索直到目标点。通过启发式搜索，可以避免搜索大量的无用节点，极大地提高了搜索效率。算法步骤如下：

1)首先创建两个空表open列表和close列表，定义起始节点为S，目标节点为K.

2)将起始节点S加入到open列表中。

3)寻找open列表中f值最小的节点a作为当前节点，若节点a是目标节点，则找到路径，退出循环，若不是，则继续下一步。

4)把当前节点a从open列表中删除并放入到close列表中，对节点a所有相邻节点进行如下判断：

a)如果相邻节点不在open列表和close列表中，将此节点添加到open列表中，用当前节点a作为该节点的父节点，并计算该节点的f值；

b)如果相邻节点已在open列表中，则再次计算该节点的f值，如果新f值小于旧f值，则用新f值替代旧f值，同时将该节点的父节点改为当前节点a；

c)如果相邻节点已在close列表中，则忽略该节点；

重复执行步骤3)和4)，若当前节点是目标节点或者open列表为空，则结束循环。

3 改进A*算法

3.1 启发函数的优化

启发函数在A*算法中具有导引作用，能够指引A*算法搜索到一条更好的路径，但是传统的启发函数存在一些效率低的问题，因此对启发函数做一些优化，改进后的启发函数为：

F(n)=G(n)+W(n)*H(n)

(3)

式(3)中，W(n)是启发函数H(n)的权重系数，添加这个权重系数可以使得启发函数的搜索效率更高，在远离目标点时，W(n)的权重系数比较大，这样可以加速算法向目标点搜索，在靠近目标点的时候，W(n)的权重系数较小，这样可以使算法搜索的路径更加的精确，通过使用优化的启发函数可以极大地提高机器人路径规划的效率。

3.2 双向搜索A*算法

双向搜索A*算法是在传统A*算法的基础上进行改进的，传统的A*算法是从起点开始搜索到终点，搜索效率比较低，双向搜索A*算法是同时从起点和终点开始搜索，即从起点向终点进行搜索，同时从终点向起点进行搜索，直到两边搜索点相交，结束搜索。双向搜索A*算法的搜索效率比较高，可以极大缩短搜索路径时间，算法步骤如下：

1)首先创建正向open表和close表，反向open表和close表，将起点S放入正向open表中，终点K放入反向open表中，同时从两端进行搜索。

2)分别从正向open表和反向open表中选取F值最小的节点作为各自的当前节点，并将其加入到各自的close表中。

3)对各自当前节点的相邻节点进行操作，若相邻节点不在open表中，则将其加入到各自的open表中，并把当前节点作为其父节点，若相邻节点在open表中，则比较其当前的F值和open表中的F值，若小于open表中的F值，则用当前F值替换open表中的F值，并将其父节点更换为当前节点，若相邻节点为障碍物或者在close表中，则跳过该节点。

4)重复循环步骤2)和3),当正向open表和反向open表为空时，表示无路径，退出循环，或者双向搜索出现交集点，表示找到路径，算法结束。

双向搜索A*算法从路径的两端开始搜索，相比于传统A*算法极大地提高了路径搜索效率。算法流程图如图2所示。

图2 改进A*算法基本流程

4 仿真结果和分析

4.1 仿真环境

为验证本文所提A*算法的有效性，采用仿真软件平台MATLAB R2020b进行仿真实验，构建20*20的栅格地图，如图3所示，图中的红色圆圈代表起点，空心方格代表终点，实心黑色方格代表障碍物。

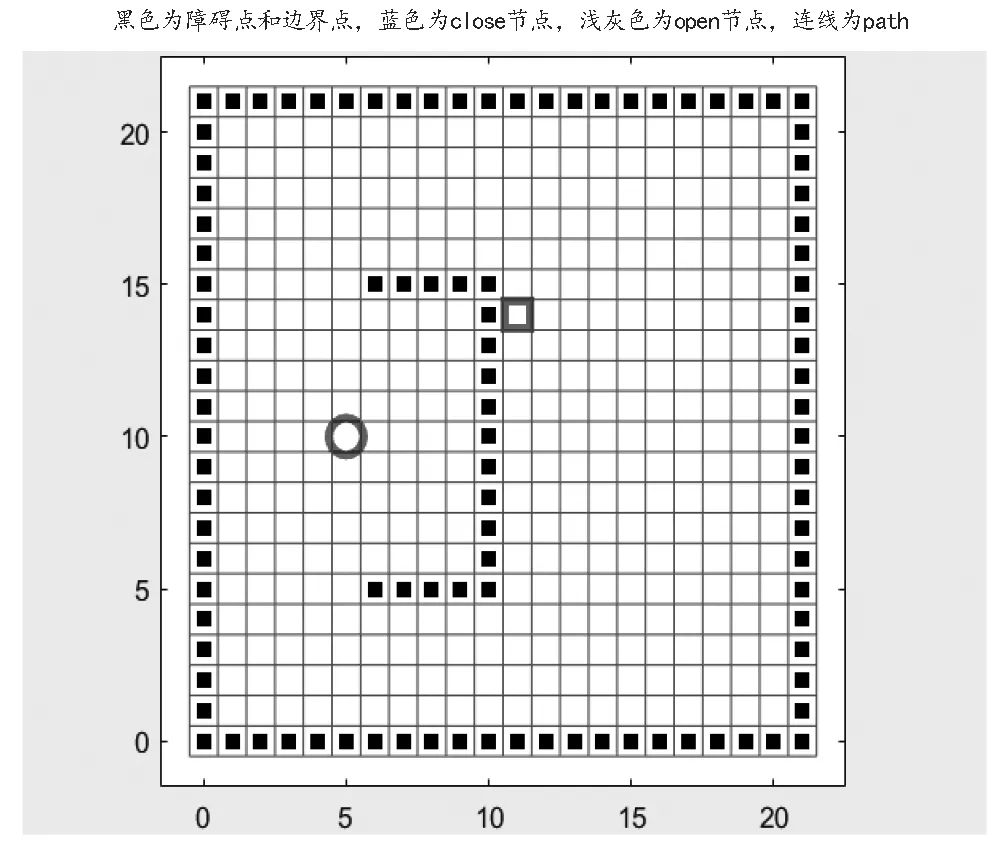
图3 20*20栅格地图

4.2 实验分析

为了对四种算法进行比较分析，采用了两种类型的地图，分别使用四种算法在两种地图上进行路径规划，两种地图路径规划的结果如图4,5所示，同时对比四种算法在两种不同地图上的路径长度，搜索节点数和搜索时间，结果如表1所示。

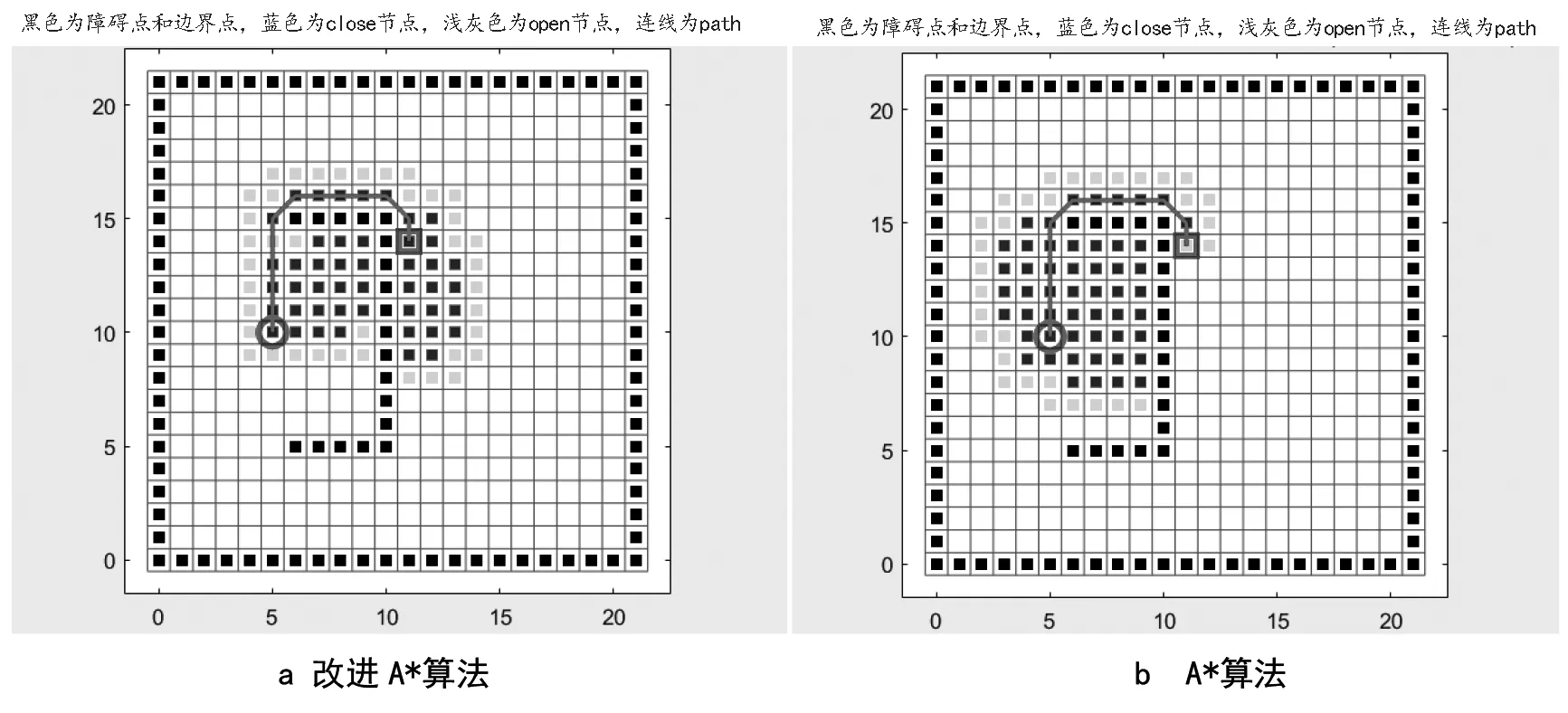
图4 地图1中四种算法路径规划结果

表1 四种算法实验数据对比

由表1可知，在地图1中，改进A*算法比传统A*算法的搜索时间减少了1.71s,搜索效率提高了14.83%，改进A*算法比BFS算法的路径长度减少了30.71m，路径长度减少了19.32%，改进A*算法比Dijkstra算法的搜索时间减少了80.05s，搜索效率提高了89.07%，搜索节点数比Dijkstra算法减少了128个，减少率达58.45%.在地图2中，改进A*算法比传统A*算法的搜索时间减少了6.08s，搜索效率提高了24.95%，搜索节点数比传统A*算法减少了13个，减少率达9.28%，改进A*算法比BFS算法的路径长度减少了50.71m，路径长度减少了24.46%，改进A*算法比Dijkstra算法的搜索时间减少了192.53s，搜索效率提高了91.37%，搜索节点数比Dijkstra算法减少了217个，减少率达63.08%.因此，采用改进A*算法进行移动机器人路径规划，不仅搜索效率高，还可以得到一条最优的路径，极大地提高了移动机器人路径规划的性能。

图5 地图2中四种算法路径规划结果

5 结论

针对移动机器人路径规划问题，传统算法搜索效率低，搜索路径不一定为最优，本文采用了改进A*算法进行移动机器人路径规划，提出了优化启发函数，加快了算法的导向能力，采用双向搜索的方式，极大地提高了算法的搜索效率，通过仿真实验可知，改进A*算法在搜索效率上比传统A*算法和Dijkstra算法要高，在路径长度上比BFS算法要短，所以，采用改进A*算法能极大地提高移动机器人路径规划的性能，具有较大的应用前景。