基于开关增益自适应的感应电机鲁棒滑模控制方法
陈华斌 ,刘伟,向德宁,陈英
(1.安徽中烟工业有限责任公司芜湖卷烟厂,安徽 芜湖 241000;2.南华大学电气工程学院,湖南 衡阳 421001;3.湖南核三力技术工程有限公司,湖南 衡阳 421001;4.湖北中烟工业有限责任公司武汉卷烟厂,湖 北 武汉 430050;5.中南大学机电工程学院,湖南 长沙 410075)
随着电力电子和微处理器技术的发展,用于变速和位置控制的感应电动机(induction motor,IM)在工业过程中的应用日益广泛,如工业机器人、工厂自动化和运输等[1-3]。然而,由于IM的系统动力学具有复杂、高度非线性、强耦合性等特征,且驱动控制对电机参数变化和负载扰动非常敏感,致使其准确、稳定控制成为难点[4-5]。
目前,针对IM的控制已有多种方法,其中,磁场定向控制(field-oriented control,FOC)应用较为广泛[6-7]。在FOC技术中,由于按转子磁链定向的矢量控制具有良好的动态和稳态性能[8],因此成为控制方法的首选。然而,由于在实际服役过程中不可避免地受到参数变化、外部负载干扰和动力学非线性等不确定因素的影响,FOC方法难以保证控制过程的稳定性[9]。为此,需要对IM进行鲁棒控制,以使其在不确定性条件下满足既定输出要求。
在已有的各类鲁棒控制方法中(如模糊控制[10-11]、滑模控制[12-14]、神经网络控制[11]等),滑模控制(sliding mode control,SMC)因其快速响应、实现简单等特性,在电气传动控制领域得到了广泛的应用[15]。然而,由于本质上的不连续开关特性,导致SMC存在固有的抖振现象。因此,通过引入自适应控制律,抑制IM在SMC下的抖振,实现电机的快速、鲁棒控制一直是SMC方法研究中的关键问题[16]。
本文旨在提出一种IM的非线性滑模控制律,根据滑模面、转子角速度及其导数引入开关增益自适应,以实现电机的鲁棒控制。另外,虽然引入开关增益自适应可以减小经典SMC方法的抖振现象,但会导致非零稳态误差的出现。因此,当电机状态轨迹接近其参考值时,通过增加一个积分器消除稳态误差,在实现鲁棒控制的同时保证算法具有更好的收敛性。通过设计相应的仿真和物理实验,利用所提方法来控制IM的转速和磁通,结果验证了方法的有效性和适用性。
1 IM数学模型
同步旋转坐标系IM的动力学模型为[17]

其中

式中:Vds,Vqs为定子电压分量;Ids,Iqs为定子电流分量;Ψdr,Ψqr为转子磁通分量;Rr,Rs分别为转子和定子绕组;Lr,Ls分别为转子和定子电感;Lm为互感;p为极对数;ωr,ωs,ωm分别为转差速度、同步转速以及转子转速;Tm为负载转矩;J为转动惯量。
通常情况下,在d-q坐标系中,有下式成立[18]:
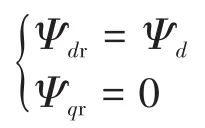
进一步,令转子磁链与d轴同向,以实现磁链和转矩之间的解耦。同时,由于0,Ψqr(0)=0),可消去式(1)中的Ψqr项,将模型式
(1)降为四阶。此时,式(1)中的第二个状态方程可重新表示为

2 控制方法设计
2.1 磁通控制
根据式(1)、式(2),可得出:

为简便起见,定义如下磁通误差
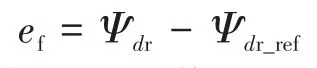
式中:Ψdr_ref为参考磁通幅值。
Ψdr则依据式(3)中的第一式通过Ids的测量值进行估计。
磁通滑模面可定义为

式中:c1为滑模面常系数。
对式(4)求导,取Ψdr_ref为常数,可得出:


式中:Uf为新的控制函数。
同时,为得出Uf的等效控制函数,对式(5)进行求解,可得出:

实际运行过程中,由于不可预测的参数变化、外部负载干扰以及动力学行为的非线性,IM的控制不可避免地存在不确定性,为消除不确定性的影响,引入如下的间断项ΔUf:
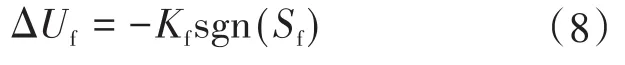
式中:Kf为增益系数。
2.2 速度控制
转子角速度调节方程可表示为

根据式(9)中的第二式,可得出:

进一步,根据式(10)以及式(9),可得出如下关于ωm的微分方程:

式中:uv为控制输入。
假设负载转矩Tm随时间缓慢变化,则式(11)可表示为

其中

角速度误差项可表示为
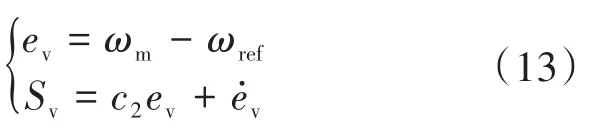
式中:Sv为角速度滑模面;ωref为基准角速度;c2为一正常数。
对式(13)的第二个方程进行求导,可得:

则uv的等效控制函数可定义为

控制函数的间断项可定义为
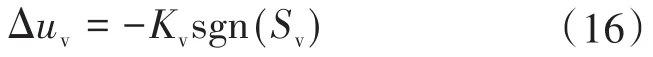
式中:Kv为增益系数。
为使滑模控制器具有更好的性能,必须选择较大的Kv值。但Kv值越大,控制变量和系统状态的抖振就越大。为了减少抖振,可在切换线两侧引入一个变宽度的边界层[18]。为进一步消除采用SMC对IM进行控制时产生的抖振,可采用光滑函数来代替不连续符号函数,例如sigmoid函数、饱和函数sat(·)或双曲正切函数tanh(·),然而,此时控制器鲁棒性将相应地降低。
本文通过对滑模面采用双曲正切函数来克服抖振问题,同时,为不损失控制的鲁棒性,引入如下的增益表达式:

上述增益可根据Sv,ωm以及进行调整,算法简单,计算量小。注意到,在选择K1,K2和K3的最佳值时应满足
2.3 鲁棒微分器设计
已有研究和实验表明,在应用Matlab微分器仿真求取电机角速度时,极易产生高频噪声。为此,引入一种基于SMC的鲁棒微分器,并将其综合应用于IM的实时控制过程。
不失一般性地,将输入信号f()t设为可测函数,并使其由具有Lipschitz常数C>0导数的基信号组成。为了修正输入信号,考虑辅助等式:

建立如下表示x和f(t)之间差异的滑模面:

对上式求微分:

利用超扭曲算法[19],将控制函数u定义为
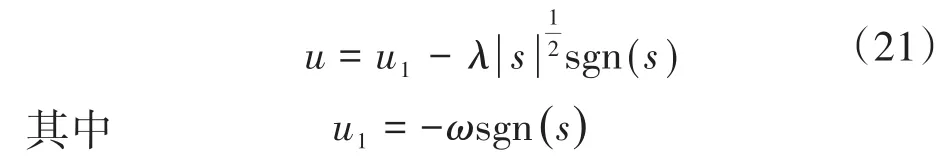
式中:λ和ω均为正数;u为微分器的输出。
图1给出了上述微分器的结构示意图。

图1 微分器结构Fig.1 Structure of the differentiator
2.4 积分器插值
为消除由扰动引起的稳态速度误差,在电机状态轨迹接近参考值时采用如下积分器:

式中:kv为积分常数;δ为阈值常数。
3 实验结果及讨论
3.1 仿真实验
首先在Matlab/Simulink环境中对控制器进行仿真性能分析,仿真结果可提供IM的动态特性信息。采用与物理实验相同的IM参数如下所示:转子绕组Rr=4.2Ω,定子绕组Rs=5.72Ω,转子电感Lr=461 mH,定子电感Ls=462 mH,定转子互感Lm=460 mH,转动惯量J=0.015kg·m2,极对数p=2,额定功率1 500 W,额定转速1 800 r/min,负载转矩Tm=(3 ±0.75) N·m,实验参考转速范围低速:-50~50 rad/s,高速:-150~150 rad/s。
首先采用周期梯形参考转速信号来研究驱动系统的跟踪性能。在测试中,传统SMC(以下简称“SMC_1”)使用如下的经典不连续控制:

式中:K为一正实数。
SMC_1策略下转子转速和定子电压分别如图2和图3所示。

图2 采用SMC_1控制的转子转速图线Fig.2 Speed of the rotor under SMC_1
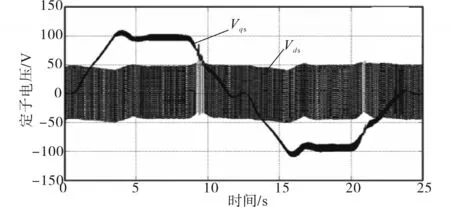
图3 采用SMC_1控制的定子电压图线Fig.3 Voltage of the stator under SMC_1
为避免抖振和噪声干扰,利用式(17)所示的SMC方法(以下简称“SMC_2”)进行转子转速控制,转子转速变化情况如图4所示,图5为SMC_2策略下定子电压分量的变化曲线。
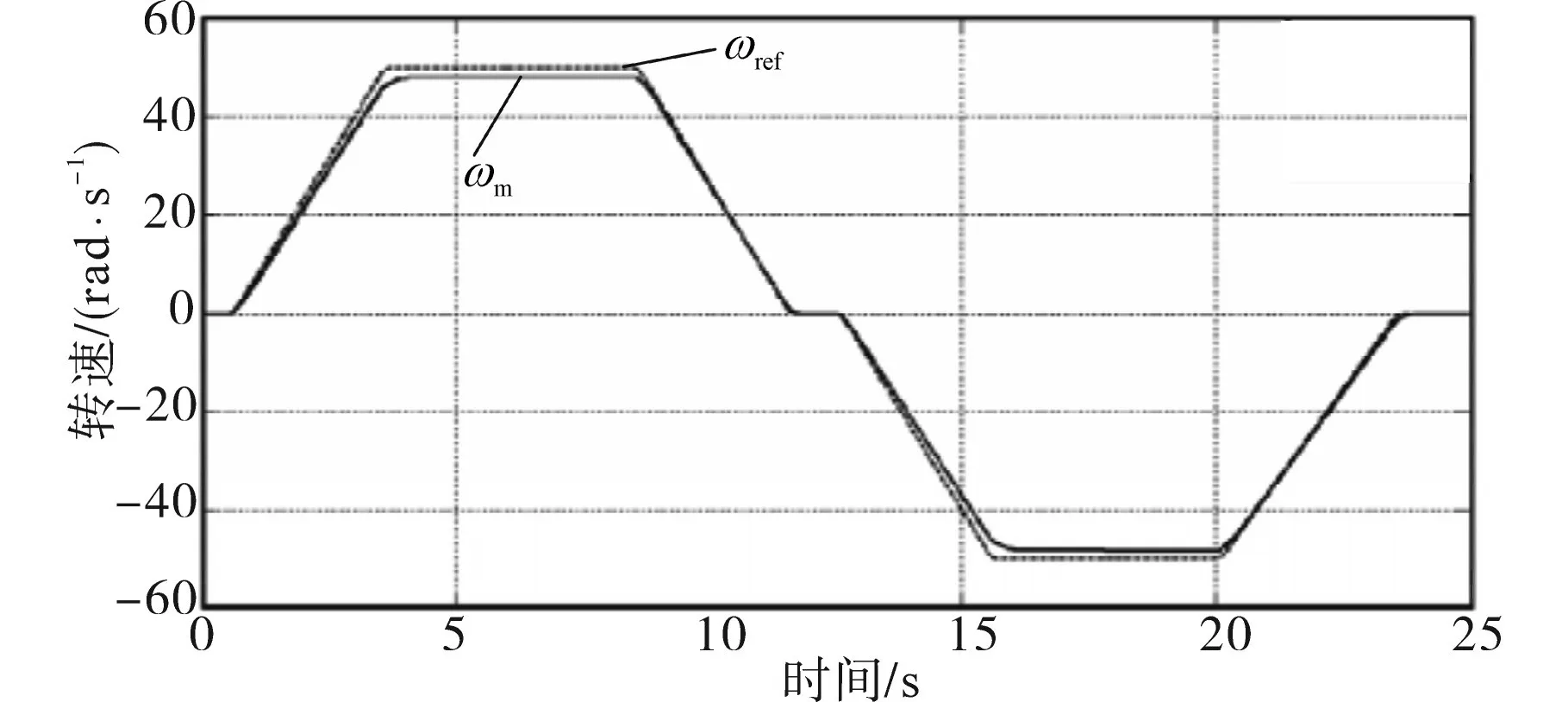
图4 SMC_2策略下的转子角速度图线Fig.4 Angular speed of the rotor under SMC_2 strategy
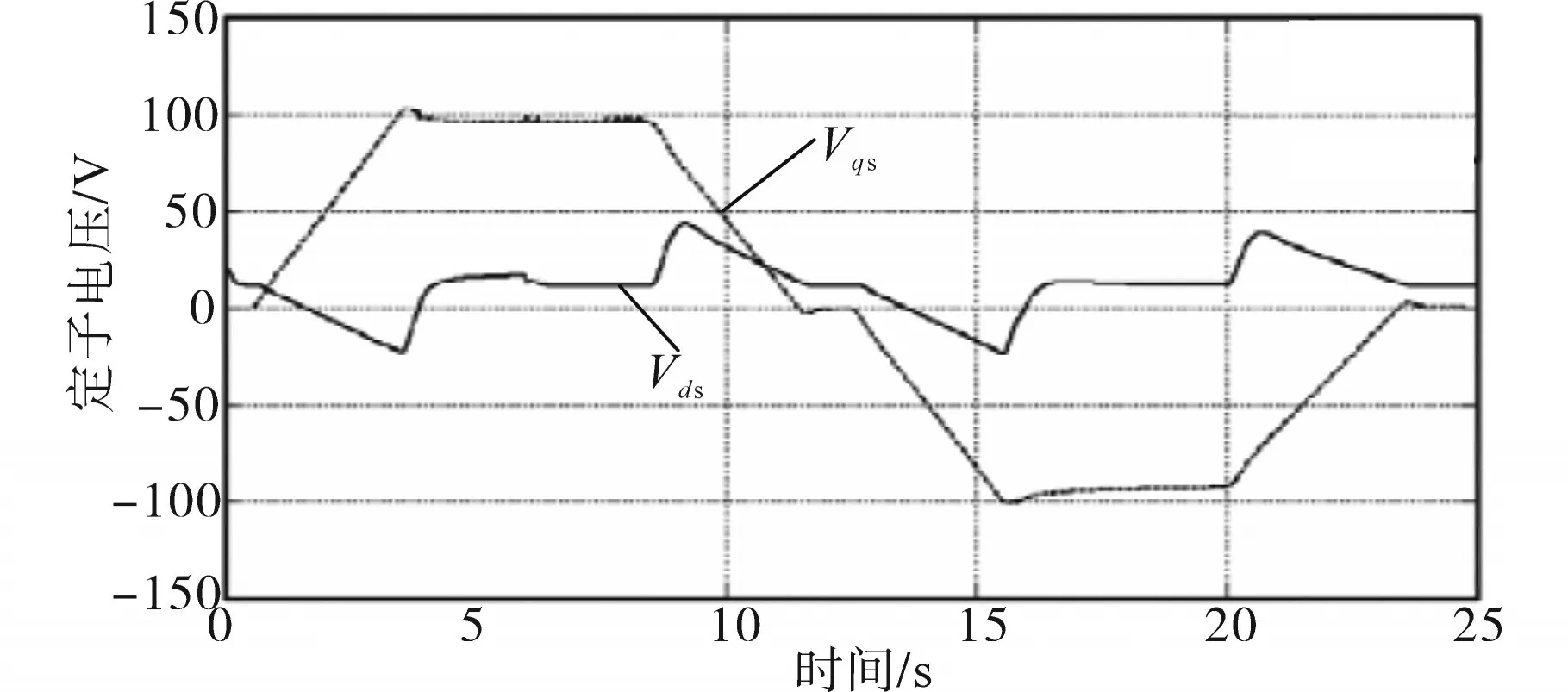
图5 SMC_2策略下的定子电压图线Fig.5 Voltage of the stator under SMC_2 strategy
进一步,为了消除扰动引起的速度稳态误差,在控制回路中引入积分器(所对应方法简称为“SMC_3”)。
图6为SMC_3方法控制下转子角速度变化情况,由图6可以看出,实际角速度稳态收敛于参考角速度。同时,由图2~图6所示,在相同条件下,虽然SMC_2相较于SMC_1的整体转速跟踪误差较大,但SMC_2方法可有效抑制定子电压的抖振,在其基础上引入积分器的SMC_3方法进一步减小了SMC_2方法的转速跟踪误差。上述三类方法的最大转速跟踪误差(maximum error,ME)、转速跟踪误差均值(average error,AE)以及转速跟踪误差标准差(standard deviation,SD)的对比参见表1。

图6 SMC_3控制策略下IM转子角速度变化图线Fig.6 Rotor angular speed with IM under SMC_3

表1 仿真实验中三类控制器转速跟踪误差对比Tab.1 Tracking error comparisons among the three control strategies in the simulation process
为模拟由于温变等条件导致的电气参数变化,在t=5 s时引入电机的电气参数跳变,其中Rs变为原值的1.5倍,Ls减小为原值的0.95倍,分别利用SMC_1以及SMC_3对IM进行控制,所得出的转速跟踪曲线如图7所示,两种控制方法的跟踪误差指标对比如表2所示。

图7 电气参数扰动条件下控制器转速跟踪仿真结果Fig.7 Rotor angular speed tracking simulations of the SMC_1 and SMC_3 strategies under electrical parameter disturbances
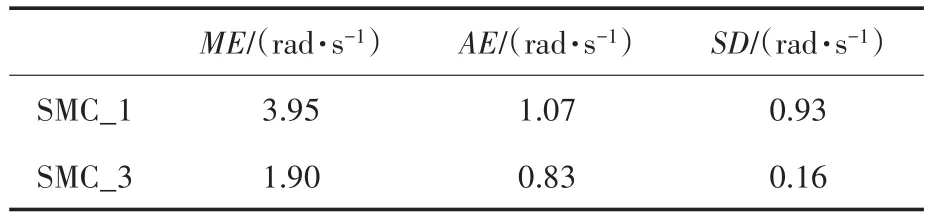
表2 参数扰动条件下SMC_1及SMC_3转速跟踪误差对比Tab.2 Tracking error comparisons between SMC_1and SMC_3 under IM electrical parameter disturbances
由图7、表2可以看出,在引入电气参数跳变时,两种控制器下转速会出现不同程度的震荡。此外,虽然SMC_1能够在一定程度上抑制电气参数不确定扰动产生的影响,但SMC_3在控制收敛速度及稳态误差抑制方面均优于传统控制器SMC_1。
最后,为进一步验证所提方法SMC_3在负载转矩扰动下的控制效果,并与后续物理实验进行对比验证,令施加在电机轴上的负载转矩在9 s到14 s之间进行变化,变化方式采取线性升降规律,变化范围为2.25~3.75N·m。转矩扰动下SMC_3的转速跟踪效果如图8所示,稳态跟踪误差为0.04 rad/s,其余各类跟踪误差指标分别为:ME=5.10 rad/s,AE=2.31 rad/s,SD=1.72 rad/s。

图8 负载扰动条件下所提控制策略的转速误差跟踪仿真结果Fig.8 Rotor speed tracking error simulation of the proposed control strategy under loading disturbance
3.2 物理实验
为进一步验证所提方法的性能,进行了物理实验,采用dSpace板(DS1104)通过适配器卡与三相逆变器相连,以驱动1.5 kW感应电动机。dSpace板的采样周期为0.1 ms,脉宽调制工作频率为5 kHz。在每个采样瞬间,dSpace板通过电流传感器和5 000点增量编码器接收所测得的电流和转子实际位置。电机负载为粉末制动器,用于产生外部干扰,以验证所提方法的鲁棒性。同时,为了证明所提函数在不同速度条件下的性能,进行了多组测试。
图9为所提SMC_3控制策略下IM的转子速度响应,其稳态速度跟踪误差收敛到约为0.075 rad/s。

图9 SMC_3策略控制下的转子实际和参考角速度Fig.9 Actual and reference rotor angular speeds under SMC_3
应用上述同样条件对电机进行高速控制,如图10所示,速度剖面在3 s内线性增加到150 rad/s,在150 rad/s下保持恒定,直到t=8.2 s,在t=11.2 s时线性减小到0 rad/s,并在0 rad/s保持1 s,然后在t=15.5 s时线性减小到-150 rad/s,在-150 rad/s下保持恒定,直到t=17 s。可以看出,在高速条件下,采用SMC_3控制策略的稳态误差接近于0 rad/s。同时,相比于低速状态,高速状态下SMC_3的最大相对跟踪误差为1.07%,这与低速状态下的最大相对跟踪误差0.97%相接近,说明了SMC_3控制策略对于高转速的跟踪精确性。

图10 SMC_3策略下实测转子角速度Fig.10 Angular speed of the rotor under SMC_3 in field test
最后,为了验证所提控制方法的鲁棒性,令施加在电机轴上的负载转矩在9~14 s之间进行变化,并将所提出的SMC_3方法与传统SMC_1方法及经典的PI控制方法进行对比,PI的各项参数设置如表3所示[20]。

表3 PI控制器增益设置Tab.3 PI controller parameters
图11显示了三种控制方法条件下转子速度变化情况,同时,三者控制效果的对比结果参见表4。

图11 三种控制方法转速跟踪Fig.11 Speeds tracking of the three control strategies

表4 物理实验中三种控制方法转速跟踪误差对比Tab.4 Speeds tracking error comparisons among the three control strategies in the field experiment
由图11、表4可以看出,相较于PI及SMC_1,所提出的SMC_3控制策略对外部负载扰动具有优良的鲁棒性。同时,在进行物理实验过程中,由于环境温度、湿度、电磁干扰及电机运转发热等因素的存在,在测试过程中所产生的实际跟踪误差的各项指标ME,AE及SD均大于仿真实验。但从稳态跟踪误差角度出发,所提出控制策略的实测效果与仿真实验具有一致性。
4 结论
针对感应电机在负载转矩、电气参数变化等不确定条件难以进行鲁棒、快速控制的问题,本文基于开关增益自适应技术,并将滑模控制与转子磁场定向控制相融合,提出了一种感应电机的鲁棒滑模速度控制方法,主要目的在于补偿由于温度和饱和效应等可能原因引起的负载转矩变化和电气参数不确定所产生的干扰效应。
在实际验证中,采用了鲁棒滑模速度控制,使感应电机具有更好的性能。同时,当电机状态轨迹接近其参考值时,通过增加一个积分器消除稳态误差,在实现鲁棒控制的同时保证算法具有更好的收敛性。最后,本文给出了各种工况下的仿真和实验结果,对所提出的控制方法的效果进行了验证。
实验结果表明,本文所提出控制方法在保留了传统滑模控制方法的鲁棒性和动态性的同时,可有效抑制电机定子电压抖振现象的产生。后续将继续研究本文所提方法在其他类型电机、更多扰动参数共存等条件下的控制鲁棒性。

